融合多角度信息和图卷积网络的社交网络节点分类模型

刘 超，梁安婷，刘小洋，黄贤英

(重庆理工大学 计算机科学与工程学院， 重庆 400054)

0 引言

当前各种在线交流分享平台发展迅猛，产生大量社交网络数据。这些数据蕴含着个体信息、个体活动及个体间的交互信息，能体现用户的属性与偏好，展示用户之间的关系等。如何挖掘社交网络数据中的信息，利用其价值一直备受研究者们关注。节点分类是将代表实体的节点进行类别划分，是社交网络的研究热点之一，有着重要的实际应用价值，例如在交流分享平台中(微博、抖音等)，对用户进行精确分类，有助于后续为用户推荐共同点更多的好友及可能感兴趣的事件，增强用户的使用体验；在电商平台中(淘宝、京东等)，精确分类买家有助于商家的把控和售卖，提高交易成功的概率。然而如何从节点自身属性和网络结构中提取更多的信息，有效融合这些信息，实现社交网络节点分类任务依然是个有待研究的问题。

同质性(homophily)和共引规律(co-citation regularity)是社会科学中的2种重要性质，源于人与人之间的交流来往。社交网络是人际网络的延伸，已有研究[1-3]证明社交网络同样具备上述性质。研究者已经利用这2种性质对社交网络问题进行了一些探索，如Getoor[4]对网络数据的近似推理算法进行了比较，在社交网络中，同质性是应用到链接分类的链接模式之一，并且链接到相同文档的文档很可能具有相同标签；Bhagat等[5]在处理带权边的多重图的标记问题时，分别利用同质性和共引规律提出了两类算法，两类算法在博客的标签分配上分别取得了较好的效果。这些研究表明，在社交网络的研究中，利用同质性和共引规律能提升解决相关问题的性能，遗憾的是，研究尚未应用到社交网络节点分类，同时，在2种性质和节点自身信息及网络拓扑结构的融合问题上，没有相关文献进行探讨。为了利用2种性质更好地挖掘并融合网络拓扑和节点自身属性，在图卷积网络(graph convolutional network,GCN)的基础上进行改进，提出能融合更多信息的模型，提高节点分类效果。基于同质性和共引规律，提取出同质型节点和共引型节点两类节点。通过相似度度量算法，计算被分类节点与其他所有节点特征向量的相似度，找到相似度最高的前k1个节点作为该节点的同质型节点；计算被分类节点与其他所有节点的邻接向量的相似度，找到相似度最高的前k2个节点作为该节点的共引型节点。对被分类节点与对应的同质型节点进行链接，构成同质矩阵空间，同理，对被分类节点与对应共引型节点进行链接，构成共引矩阵空间。分别在2种矩阵空间进行卷积，提取相应的节点信息，对被分类节点进行信息补充，提高分类精确度。

在Wang等[6]的研究基础上，利用上述两类节点，挖掘更全面的信息并进行融合，提出融合多角度信息和图卷积网络的社交网络节点分类模型(a social network node classification model based on multi-angle information fusion and graph convolutional network,MAIF-GCN)。主要贡献如下：

1) 提取蕴含着节点同质信息和共引信息的两类关系型节点。①同质型节点：和被分类节点有着相似属性(特征向量相似度高)的节点；②共引型节点：和被分类节点链接着更多相同节点(邻接向量相似度高)的节点。提取两类关系节点的信息，即挖掘被分类节点的隐藏信息，后续实验证明，提出的两类关系节点能对被分类的社交网络节点信息进行更好地补充，对社交网络节点分类有益。

2) 提出一种新的融合多角度信息和图卷积网络的节点分类模型MAIF-GCN。从邻接邻居、同质最近邻和共引最近邻多个角度挖掘被分类节点的相关信息，通过平均嵌入相加、注意力机制进行信息融合，实验证明，该模型在传统社交网络数据集上取得很好的分类效果。

1 相关工作

Kipf等[7]和Defferrard等[8]提出的GCN能有效捕捉节点的相关信息，在节点分类问题上表现出很好的分类效果，是处理节点分类问题的常用方法。如Derr等[9]利用平衡理论来正确地汇总和传播经过签名的GCN模型各层的信息，使分类问题泛化至社交媒体中的签名网络(或既有正面链接又有负面链接的图表)；Hu等[10]为了增加接收域，提出了一种新的深度层次图卷积网络(hierarchical graph convolutional networks,H-GCN)用于半监督节点分类；Lin等[11]提出了基于图卷积网络的结构融合，从多视图数据的多图结构中挖掘出更完整的分布结构，以半监督的方式提高引文网络节点分类性能。

GCN的巨大成功部分归功于它提供了一种基于拓扑结构和节点特征的融合策略来学习节点嵌入，然而，最近的一些研究揭示了GCN在融合节点特征和拓扑结构方面的某些弱点。例如，Li等[12]的研究表明，GCN实际上对节点特征进行了拉普拉斯平滑，使嵌入到整个网络中的节点逐渐收敛；Hoang等[13]和Wu等[14]证明了特征信息在网络拓扑结构上传播时，拓扑结构对节点特征起到低通滤波的作用；Wang等[6]通过实验证明，GCN对网络拓扑结构和节点特征的融合能力与最佳甚至令人满意的距离相去甚远。

无法充分融合节点自身属性和网络拓扑结构来提取相关信息，可能会严重影响GCN在分类任务中的性能，为解决此问题，不少研究者在GCN的基础上进行改进：Velikovi等[15]提出了图注意网络(graph attention network,GATs) ，他们为一个邻域中的不同节点指定不同的权值，以此调整从邻居节点接收的信息量，提高分类精确度；Abu-El-Haija等[16]提出了一个利用邻接矩阵的多次幂的图卷积层，通过堆叠高阶卷积层获取更多信息，达到提高分类精度的效果；Wu等[17]提出了一个名为DEMO-Net(degree-specific graph neural networks)的通用图神经网络模型，该模型根据节点的度值将特征聚合表达为一个多任务学习问题。这些改进方法都在一定程度上提高了节点分类的精度，在处理节点分类问题上起着不可忽视的作用，可见，更好地融合网络拓扑结构和节点信息，更多地提取相关信息，是提高节点分类效果的先决条件，是解决节点分类问题的重要目标。

Bhagat等[18]在发表的社交网络节点分类研究综述中，提到社交网络存在的2个重要特性：一为同质性，即个体之间的联系与那些在本质上相似的个体相关；二为共引规律，即相似的人倾向于提及或联系相同的事物。然而，对这2个重要特性的研究尚未应用到社交网络节点分类领域。Wang等[6]就GCNs能否在信息丰富的复杂图中最优地整合节点特征和拓扑结构进行研究，针对GCNs融合节点特征和拓扑结构的能力不够理想的缺陷，提出了一种用于半监督分类的自适应多通道图卷积网络(adaptive multi-channel graph convolutional networks,AM-GCN)。其核心思想是同时从节点特征、拓扑结构及其组合中提取特定的和共同的嵌入，并利用注意机制学习自适应嵌入的重要性权重。在进行节点特征和拓扑结构信息融合的过程中，AM-GCN无意识地使用了同质性，受其使用方法的启发，本文中从理论上证明为何该构建方法能够对分类点信息进行补充，并进一步添加共引规律，构建能提取更多信息、融合信息更完整的分类模型。

2 提出的MAIF-GCN模型

2.1 问题描述

为研究社交网络节点分类问题，在给定图数据G= (A,X)的条件下，尽可能精确地将图中的n个节点分为C类中的某一类，使用的符号定义即变量描述如表1所示。

表1 符号定义

为解决上述问题，提出了融合多角度信息和图卷积网络的节点分类MAIF-GCN模型，模型概览如图1所示。

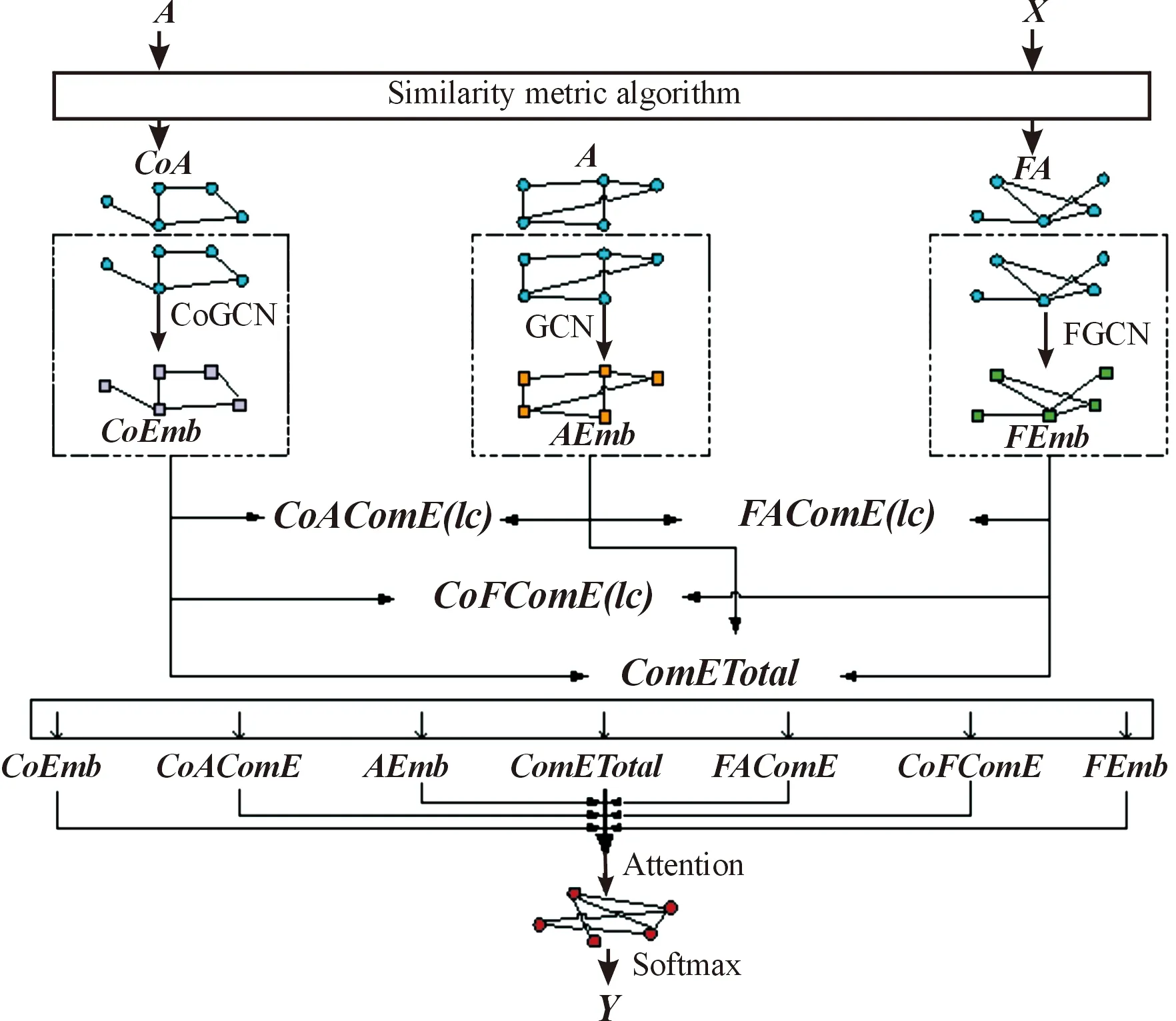
图1 融合多角度信息和图卷积网络的社交网络节点分类模型(MAIF-GCN)

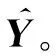
2.2 构造2个矩阵空间

为了提高社交网络节点分类精度，基于社会科学中确定的2个可以应用于在线社交网络的重要现象——同质性和共引规律，提出两类能为分类节点提供有用信息的相关节点——同质型节点和共引型节点。为挖掘两类节点信息，构造相应的关系矩阵空间，在构建好的关系矩阵空间中进行卷积操作，就能融合相应关系的节点信息。

X是特征向量矩阵，该矩阵每一行代表着一个节点的特征，将一行向量同其他所有行向量进行相似度的计算，便能求得这些其他节点同这个节点在特征即性质上的相似程度。通过对特征向量矩阵的每一行和其他行进行相似度的计算，得出和每个节点性质最相似的k1个节点。将“性质相似”这种联系作为边，相似度最高的k1个节点将产生链接，由此得出每个节点的同质向量FAi∈R1×n，将所有节点的同质向量拼接起来，得到同质矩阵空间FA∈Rn×n。

A是邻接矩阵，该矩阵每一行代表着一个节点同其他节点的联系，存在联系则为1，否则为0。将一行向量同其他所有行的向量进行相似度的计算，便能求得其他所有节点同该节点偏好或倾向最相近的k2个节点。将“偏好或倾向相近”这种联系作为边，倾向相近度最高的几个节点将产生链接，否则不链接，由此得出每个节点的共引向量CoAi∈R1×n，将所有节点的共引向量拼接起来，得到共引矩阵空间CoA∈Rn×n。

经过上述理论铺垫发现，2种矩阵空间都是由求解向量间相似度获取的。常见的相似度的计算有欧几里得度量、皮尔逊相关系数、余弦相似度等。通过对比计算，几种相似度度量算法对最近邻的计算结果几乎一致，此种算法的选择不影响最终分类结果。本文中最终使用余弦相似度进行相似度的度量：

(1)

2.3 提出的融合多角度信息和图卷积网络的社交网络节点分类模型MAIF-GCN

2.3.1获取空间嵌入

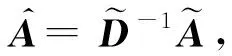
在共引矩阵空间进行图卷积，提取并融合共引型节点的节点信息，得到共引矩阵空间卷积后的嵌入ZCo(CoEmb)， 其中，Wco是在共引矩阵空间进行学习的权重矩阵：

(2)

在邻接矩阵空间进行图卷积，提取并融合邻居节点的节点信息，得到邻接矩阵空间卷积后的嵌入ZA(AEmb)，其中，WA是在邻接矩阵空间进行学习的权重矩阵：

(3)

在同质矩阵空间进行图卷积，提取并融合同质型节点的节点信息，得到同质矩阵空间卷积后的嵌入ZF(FEmb)，其中，WF是在同质矩阵空间进行学习的权重矩阵：

(4)

2.3.2融合空间嵌入

不同社交网络中，三类节点向被分类节点提供的信息的重要程度不同，有时可能只有单一类型的节点提供对分类有帮助的信息，但有时需要2种或3种关系节点共同提供信息。

邻接矩阵空间、同质矩阵空间和共引矩阵空间3种单空间都经过了相同的预处理，因此在3种单空间进行卷积后的嵌入输出格式一致，即矩阵大小一致，可以直接进行加减。 将单空间嵌入通过相加平均进行组合，节点会融合不同空间卷积后的信息，得到联合嵌入。

将单空间嵌入、两两单空间联合嵌入和3个单空间联合嵌入共同放进注意力机制进行融合，得到最终嵌入，同时获得各种嵌入的重要性。由上述获取联合空间嵌入的操作易知，单空间嵌入与联合空间嵌入输出格式一致。将所有嵌入在第二维上进行拼接，得到每个节点在不同角度上的多维表示。本文的注意力机制使用两层全连接进行学习，再通过softmax函数，从每个节点在不同角度上的多维表示，学习到分类该节点时在每个角度，即每种嵌入上所占的比重。

1) 组合单空间嵌入(eg：共引与邻接单空间嵌入组合ZCoA(CoAComE)，3个单空间嵌入组合ZTotal(ComETotal))：

(5)

(6)

2) 融合空间嵌入：

(αCo,αA,αF,αCoA,αFA,αCoF,αTotal)=

att(ZCo,ZA,ZF,ZCoA,ZFA,ZCoF,ZTotal)

(7)

将3种单空间嵌入和联合嵌入共同放进注意力机制，通过注意力机制得到每个节点对应各种嵌入的重要性，使用该表示重要性的向量将各种嵌入融合起来，得到终极嵌入Z(Emb)：

Z=αCo·ZCo+αA·ZA+αF·ZF+

αCoA·ZCoA+αFA·ZFA+αCoF·ZCoF+

αTotal·ZTotal

(8)

2.3.3半监督多标签分类

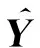
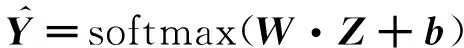
(9)

2.3.4约束和目标函数

1) 一致性约束

考虑到虽然提取信息的角度不同，但最终信息给予的对象是同一节点，因此，这些不同的信息会有些许相似或存在某种联系。通过将不同关系矩阵空间中提取到的信息进行相互约束，使得挖掘到的信息更有利于分类。这种相互约束，就是提取出的信息的一致性约束。

各嵌入在正则化后乘以自身的转置转化为对称矩阵，用对称矩阵的最小二乘进行一致性约束。邻接矩阵嵌入ZA正则化后表示为ZAnor，同理，同质矩阵嵌入、共引矩阵嵌入正则化后的表示为ZFnor、ZConor。正则化后的不同空间嵌入乘以自身的转置转化为对称矩阵，分别得对称阵如下：

(10)

以邻接矩阵和同质矩阵为例，用最小二乘得此2种空间嵌入的一致性约束LCoA如下：

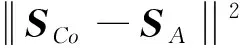
(11)

同理可得邻矩和共引矩阵嵌入的一致性约束LFA，同质矩阵和共引矩阵嵌入的一致性约束LCoF。不同网络对于矩阵空间的相似性要求不同，通过对一致性约束进行加权相加，得到总的一致性约束：

(12)

式中：α、β为超参数，不同网络通过调节α、β来调整各空间嵌入的一致性约束。

2) 目标函数

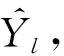
(13)

3) 综合目标函数

结合一致性约束和目标函数，得到模型的综合目标函数L：

L=Lt+θ·LCom

(14)

式中：θ为超参数，不同网络的数据集在经此模型训练时，通过调节此超参数对一致性约束的权重进行调整。

算法1模型算法流程。

输入：社交网络图数据G=(A,X)，L个带标签的样本节点；

1) 通过式(1)得到FA和CoA；

repeat：

3) 通过式(2)—(4)分别计算得到单空间嵌入ZCo、ZA和ZF，通过式(5)与式(6)获取组合空间嵌入ZCoA、ZFA、ZCoF与ZTotal；

4) 使用式(7)获得不同嵌入的比重(αCo,αA,αF,αCoA,αFA,αCoF,αTotal)，式(8)加权融合，得到最终嵌入Z；

6) 通过式(10)—(12)计算一致性约束LCom，式(13)进行交叉熵损失求和，得到Lt；

7) 使用式(14)得到综合目标函数L；

8) 梯度下降法更新模型参数；

until 满足训练停止条件

3 实验与结果分析

3.1 实验设置

3.1.1数据描述

使用2个传统社交网络数据集BlogCatalog[19]和Flickr[19](数据集信息见表2)，以分类准确率(accuracy)与F1-measure作为度量指标，测试本文提出的MAIF-GCN模型。在BlogCatalog和Flickr数据集上，将本文模型与传统的社交网络节点分类算法及一些先进的GCNs变体模型进行对比，并结合试验结果对模型进行分析。

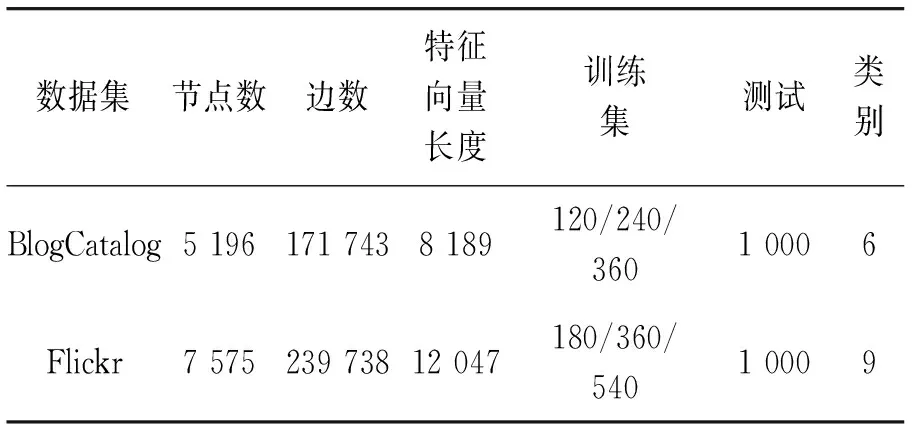
表2 用于模型测试的数据集信息

1) BlogCatalog数据集：一个社会关系网络。节点属性由用户配置文件的关键字构造，图是由博主和他(她)的社会关系(比如好友)组成，标签代表作者提供的主题类别，所有节点划分为6类。

2) Flickr数据集：Flickr是用户分享图片和视频的社交网络。节点表示Flickr中的用户，图是用户之间的好友关系，标签用于标识用户的兴趣小组，所有节点划分为9类。

3.1.2对比实验

将MAIF-GCN模型与6种先进且效果良好的图神经模型进行对比，对比模型详情如下：

1) GCN[7]：一种半监督图卷积网络模型，它通过聚合邻居的信息来学习节点表示。

2) Chebyshev[8]：一种基于切比雪夫滤波器的GCN方法。

3) GAT[15]：一种利用注意机制聚集节点特征的图神经网络模型。

4) DEMO-Net[17]：一种用于节点分类的度数特定图神经网络。

5) MixHop[16]：一种基于GCN的方法，在一个图卷积层中混合高阶邻居的特征表示。

6) AM-GCN[6]：一种用于半监督分类的自适应多通道图卷积网络。

3.1.3参数设置

如表2数据集所示，训练集有3种标签率(如BlogCatalog数据集存在120、240、360个标签节点)，2个数据集都选择1 000个节点作为测试集。所有对比模型都在他们相应论文建议的参数基础上进行调优，以求更高的精度。除本文模型外，模型AM-GCN的分类结果都优于其他模型，为了方便对比，本文模型与AM-CGN模型共有的参数，取值与该模型一致，在3个不同的矩阵空间进行两层图卷积，2个数据集的隐藏层nhid1都是512，输出层nhid2都是128；120个标签节点的BlogCatalog数据集使用0.000 2的学习率进行Adam优化，180个标签节点的Flickr数据集使用0.000 3，除此之外，2个数据集的其他训练集都用0.000 5作为优化函数的学习率。一致性约束系数θ和所取同质型节点的个数k1及共引型节点的个数k2值将在后文进行讨论，根据分析结果取值，最终设置BlogCatalog数据集的一致性约束系数θ为1，k1取值为5，k2取值为6；Flickr数据集的一致性约束系数θ为0.1，k1取值为6，k2取值为3。

3.2 实验结果与分析

3.2.1实验结果

社交网络节点分类对比实验结果见表3。由实验结果可以得出，MAIF-GCN的准确率(Accuracy)与F1-measure在2个数据集上都优于所有对比模型。事实上，除却本文中提出的MAIF-GCN，AM-GCN的准确率和F1-measure都是最高的， 已被提出者证明其信息融合能力的优越，而MAIF-GCN在此模型分类结果的基础上，将BlogCatalog数据集的分类精确度和F1-measure指标提高3%及以上，将Flickr数据集的分类精确度提高3%及以上、F1-measure指标提高2%及以上，充分说明本文模型在引入社会科学中的2种性质后，具有更进一步的信息挖掘与融合能力，证明了提出的两类型节点在解决社交网络节点分类时具有积极作用。

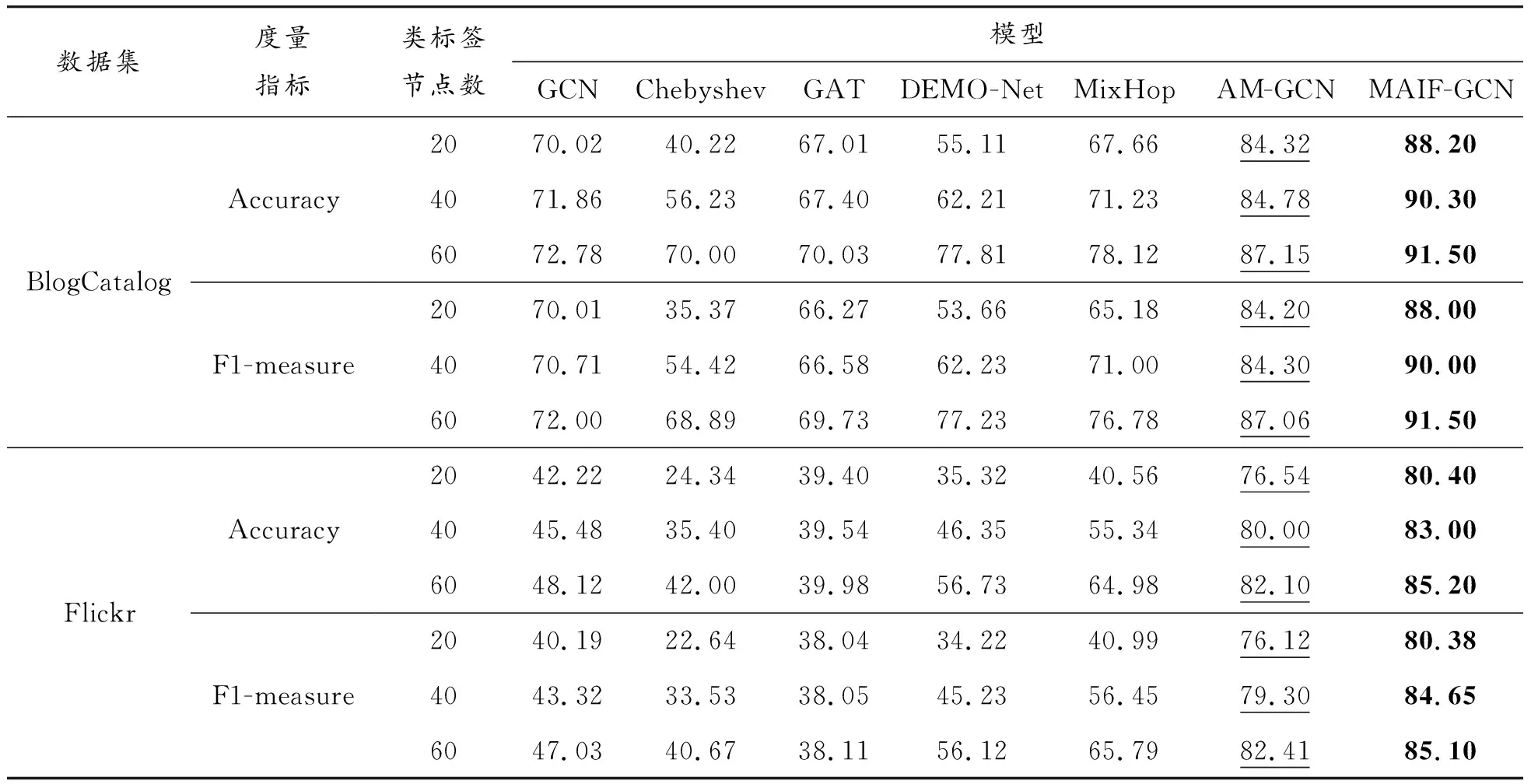
表3 社交网络节点分类实验结果

3.2.2嵌入分布分析

可视化各种嵌入方式的占比，直观表示不同嵌入方式在分类时的占比情况，观测提取的两类型节点在社交网络节点分类中的作用。单空间嵌入、两两单空间联合嵌入和3个单空间联合嵌入共同放进注意力机制进行融合，在得到最终嵌入的同时，获得各种嵌入的重要性。下载训练过程中各嵌入的注意力值，使用箱须图进行绘制，得到嵌入分布分析如图2所示。

Blogcatalog数据集上各嵌入方式(箱须图横轴从左往右)占比均值分别为：0.013，0.434，0.149，0.045，0.265，0.029，0.065；Flickr数据集上分别为：0.010，0.822，0.017，0.026，0.094，0.011，0.020。

从图2和嵌入占比均值可以直观地看到每种嵌入的分布情况，并且总结出以下结论：① 同质矩阵单空间嵌入在2种数据集中都占比最高，远超传统邻矩，充分说明在社交网络节点分类中，同质型节点对分类节点的正向作用；② 同质和共引矩阵空间的融合嵌入在2种数据集的嵌入中都占比次高，且在2个数据集的嵌入中，共引矩阵单空间嵌入都比邻接矩阵单空间嵌入要高，这两点证实了共引型节点同样对被分类节点的精确分类有益；③ 单空间嵌入占比较大，但融合嵌入的比例同样不可忽视，因此，在社交网络节点分类时，要挖掘融合多方面的信息，才能对节点进行精确分类。

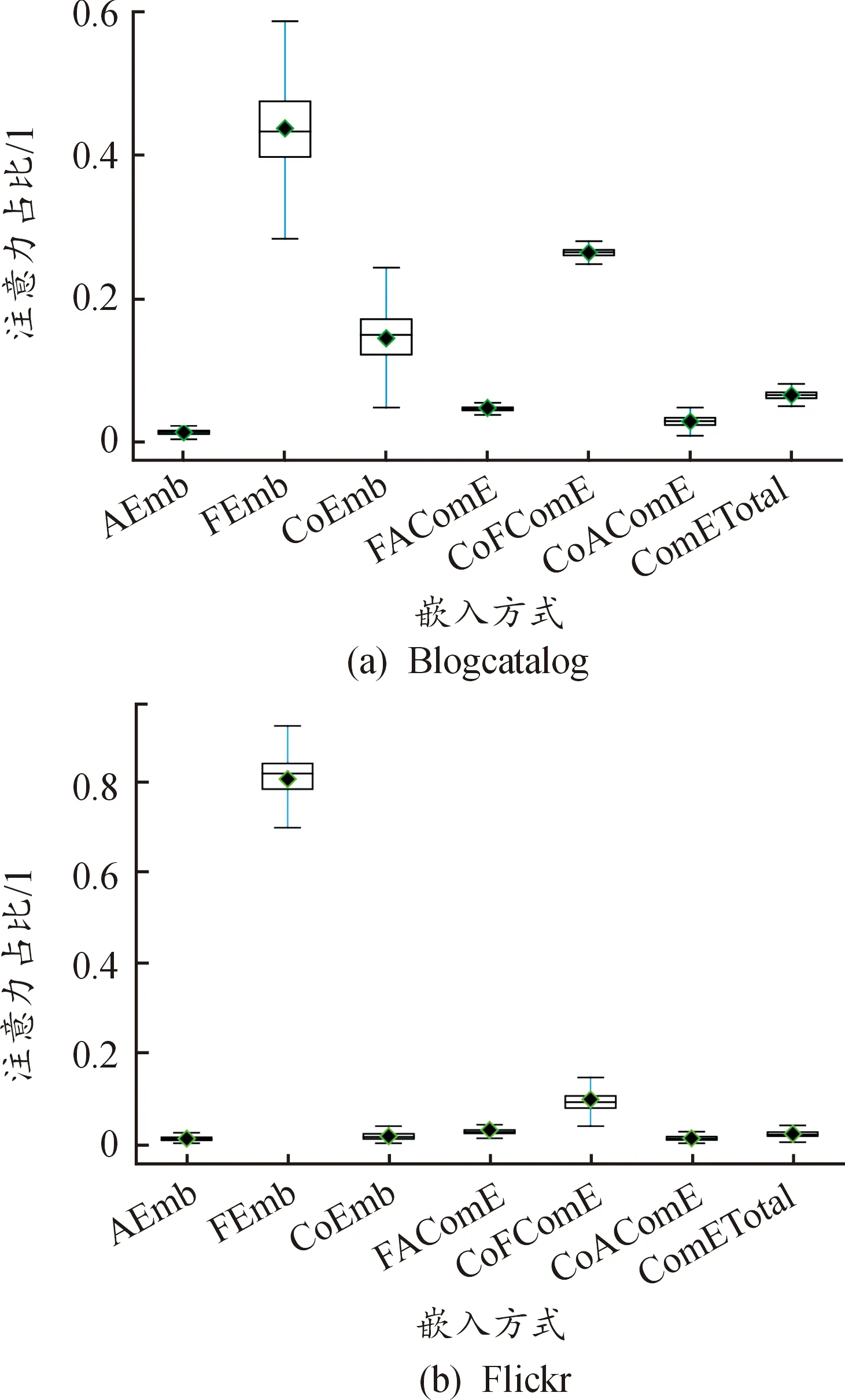
图2 嵌入分布分析

3.2.3参数分析

本文模型的超参数有k1、k2、θ、α、β。参数k1和k2是获取的：“近邻”个数，这里的“近邻”并非直观意义上的位置相近，而是同质或共引意义相近。基于六度空间理论，k1、k2取值范围以数字6为中心，分别测试两类型的“近邻”个数从2～9对分类产生的影响。图3展示了k1取值(2～9)对节点分类精度的影响，图4展示了k2取值(2～9)对节点分类精度的影响。

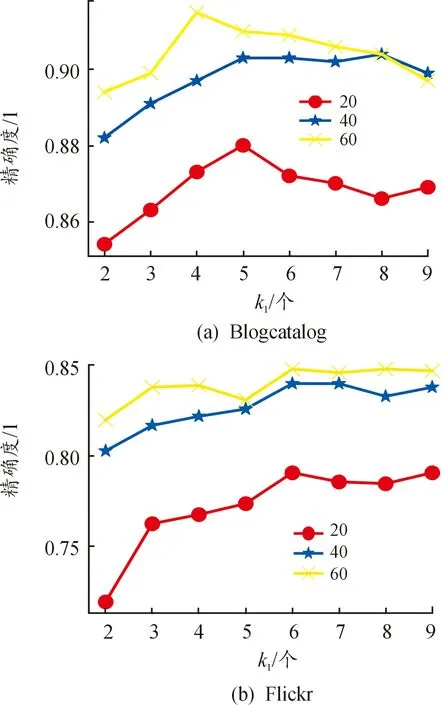
图3 参数k1分析

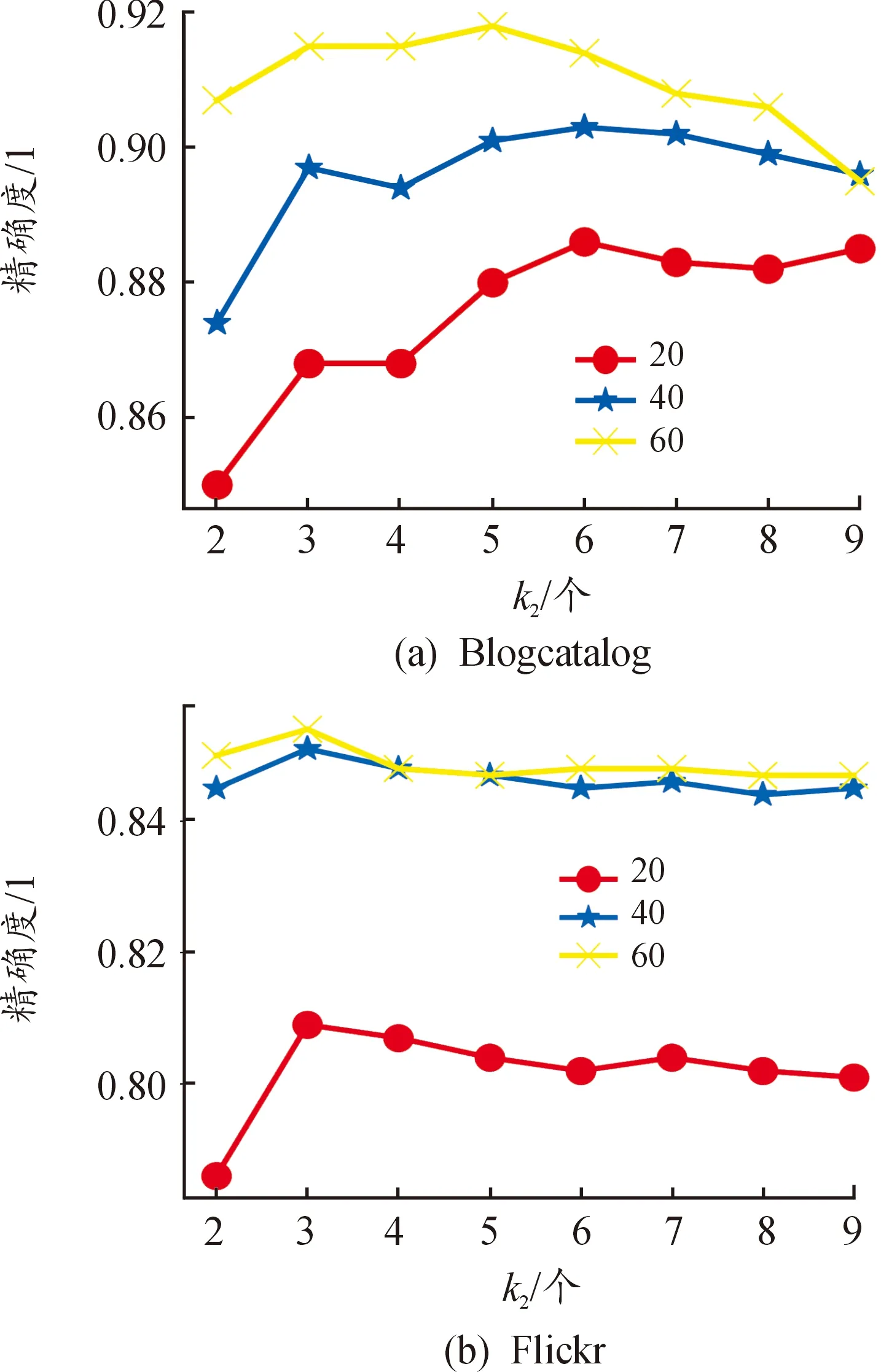
图4 参数k2分析

参数θ是损失函数中共同一致性约束的系数，调整θ即改变一致性约束对节点分类影响的力度，图5展示了θ取值(0.000 1～10 000)对节点分类精度的影响。

α、β是共同一致性约束中，2种单独一致性约束的系数，调节α、β值，就能调整3种单独一致性约束在共同一致性约束中的占比。3种约束的占比情况由α、β共同决定，2个参数的实验数据单独进行可视化不够直观，将每组α、β的实验数据同时绘制，以便分析出更合理的超参数配比。图6、图7分别展示了α、β取值(0.000 1～10 000)对Blogcatalog、Flickr数据集节点分类精度的影响。

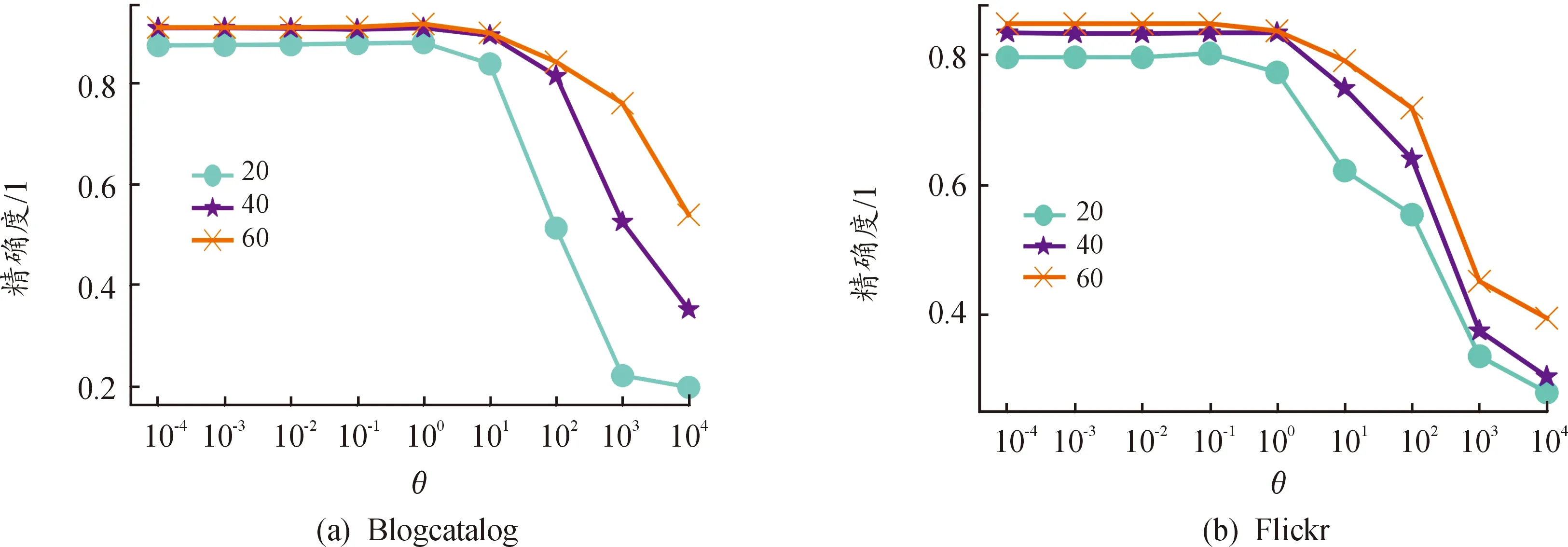
图5 参数θ分析

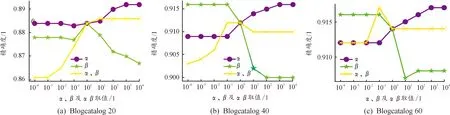
图6 参数α、β分析(Blogcatalog)

图7 参数α、β分析(Flickr)

同质最“近邻”参数k1的分析见图3，BlogCatalog随着k1值的增加，分类精确度先增加再减少，类标签数为20、40、60的数据集分别在k1取5、8、4处获得最优。这可能是因为BlogCatalog随着图变得更密集，特征平滑，而且更大的k1可能引入更多的噪声连边。而Flickr的精确度在中间存在小波峰，随着k1值的增加，精确度先增大后减小再趋于平缓，它可能同样受特征平滑和噪声的影响，类标签数为20、40、60的Flickr数据集都在k1取6或9处获得最优。

共引最“近邻”参数k2的分析见图4。图4中，BlogCatalog在类标签数为20时，精确度随k2的增加先增大后减小再趋于平缓，k2在6或9处取得最优；当标记数据增多，随着k2值的增加，BlogCatalog的分类精确度先增加再减少，与k1情况相似，可能因BlogCatalog变得密集，特征平滑，或引入更多的噪声连边，类标签数为40和60的BlogCatalog数据集分别在k2取6和5处获得最优效果。Flickr的精确度波动小，同样是随着k2值的增加，精确度先增大后减小，原因与BlogCatalog数据集一致，类标签数为20、40、60的Flickr数据集，都在k2取3时获得最佳效果。

共同一致性约束θ的分析见图5，2个数据集的精确度，都随着一致性约束系数θ的增加，先非常缓慢的上升，而后，BlogCatalog数据集以1为拐点，Flickr数据集以0.1为拐点，精确度随着θ值的增加下降。两数据集分别在θ取1和0.1左右获得最优效果。现象表明，2个数据集都不期望从3个空间中提取出太相似的信息。

一致性约束系数α、β分析见图6、图7。如图6(a)所示，圆形标记实线是超参数α的消融实验结果，此时β恒为1(第3种单独约束系数一直为1)，反映α对应的单独约束的占比对分类结果的影响；星形标记线是超参数β的消融实验结果，此时α恒为1，反映β对应的单独约束的占比对分类结果的影响；X形标记线是超参数α、β同时进行消融实验的结果，此时第3种单独约束仍为1，α、β取值的一致变化将改变第3种单独约束的占比，反映了第3种单独约束的占比对分类结果的影响，α、β取值越大，第3种约束占比越小。将每个数据集的3种单独约束对分类结果的影响可视化到同一张图上，观测分析超参数α、β的配比。

图6中，所有子图中的圆形标记线大体呈上升趋势，α取值大，分类效果较好；子图(a)中除波峰，星形标记线大体呈下降趋势，β取值较小，分类效果好；子图(c)中除波峰，星形标记线大体呈上升趋势，说明第3种约束占比小，α、β取值大于等于1(第3种单独约束系数一直为1)。子图(a)中，在类标签数为20的Blogcatalog数据集中，圆形标记实线大体呈上升趋势，在1 000处达到峰值，星形标记线在1处取得最大值，X形标记线在10处取得最大值，再往后对精确度没有影响，说明α对应约束占比最大，第3种约束占比最小，β值对应约束较为折中取得最佳效果，但因X形标记线后面趋于平缓，α取值不适宜过大。综上，α值取100左右，β值取10左右时，模型效果较好；在类标签数为40和60的Blogcatalog数据集中，圆形标记实线呈上升趋势，在1 000处达到峰值，星形标记线和X形标记线都在0.1处取得最大值，β对应约束应比另外两约束小，α值取10左右，β值取0.1左右时，模型效果较好。

图7中，3个子图的圆形标记实线和星形标记线走向几乎相反，说明在Flickr数据集上，类标签个数对一致性约束占比有影响，需要逐个分析。图7(a)中，圆形标记实线在0.1处取得最大值，星形标记线和X形标记线都在10处取得最大值，α值对应一致性约束占比小，β值对应一致性约束占比大，第3种约束占比小。综上，在类标签数为20的Flickr数据集上，α值取1,获得的模型效果较好，β值取10左右模型效果较好。图7(b)中，圆形标记实线不随值的变化改变走向，星形标记线和X形标记线都在10处取得最大值，β值对应一致性约束占比大，第3种约束占比小，α值对应一致性约束的占比比β大，比第3种约束小，α值取5左右，β值取10左右获取的模型效果较好。图7(c)中，圆形标记实线在10处达到最大值，且取值再往上精确度不变，星形标记线在0.1处取得最大值，X形标记线在100处取得最大值，第3种约束占比最小。综上，α值对应约束占比大，β值对应约束占比小，但比第3种约束占比大，α值取5左右，β值取10左右获取的模型效果较好。

对不同数据集，给出的α、β近似值的模型的分类结果比取距离该近似值较远的值高0.2%～0.8%，且分类精确度对α、β的取值不敏感，一定范围(20左右)内变化非常小，可忽略不计。

3.2.4剥离实验分析

为了进一步评估本文模型各模块的有效性，进行剥离实验，将MAIF-GCN及其4种变体在所有数据集上的分类结果进行比较。对比分类实验结果见表4。

1) GCN：没有同质矩阵空间和共引矩阵空间的MAIF-GCN模型。不存在同质矩阵空间和共引矩阵空间的嵌入，节点只在邻接矩阵空间进行卷积操作，进而分类，模型退化为传统的GCN模型。

2) MAIF-GCN-F：没有同质矩阵空间的MAIF-GCN模型(只有邻接矩阵嵌入、共引矩阵嵌入及两者的组合嵌入)。

3) MAIF-GCN-Co：没有共引矩阵空间的MAIF-GCN模型(只有邻接矩阵嵌入、同质矩阵嵌入及两者的组合嵌入)。

4) MAIF-GCN-cst：去掉一致性约束的MAIF-GCN模型。不对各单空间嵌入进行一致性约束，只通过模型训练，将各种嵌入进行组合和融合，进而进行分类的MAIF-GCN模型。

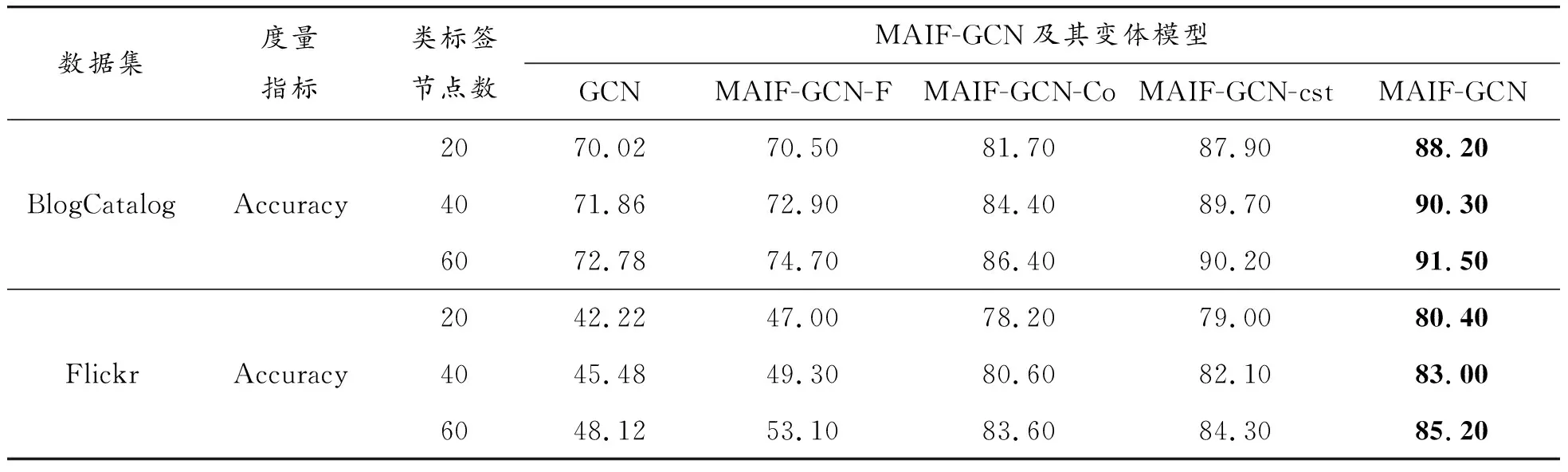
表4 MAIF-GCN及其变体模型节点分类实验结果

分析表4，可以得出以下结论：① MAIF-GCN的结果始终优于其他4种变体，表明引入并结合利用同质矩阵和共引矩阵空间，进行3种单空间嵌入的一致性约束是有效的。② MAIF-GCN-F和MAIF-GCN-Co的分类精确度都比GCN的高，分别表明了共引矩阵空间和同质矩阵空间的有效性。③ MAIF-GCN-Co的结果比MAIF-GCN-F好，意味着同质性在本模型中起着更重要的作用。④ 对比MAIF-GCN-cst和表3中的其他实验结果可以发现，MAIF-GCN-cst虽然没进行约束，但仍取得了对抗baseline的非常有竞争力的表现。

3.2.5不同类型数据集验证实验

为了进一步验证所提出模型的效性，验证利用2种性质在解决社交网络节点分类问题时真实有效，使用不同类型的数据集进行对比实验分析。

将社交网络数据集ego-Facebook[20]中的2个网络进行处理，用于节点分类对比实验。该数据集因收集的节点特征不同分为10个小网络，取其中缺失标签较少、节点个数较多，且类别较多的网络0(后称FaceNet_0)和网络1912(后称FaceNet_1912)进行实验，清洗掉网络中缺失特征或标签的节点，进行数据规整化后进行分类，验证模型在分类类别较多时的性能。同时，使用另一社区检测数据集UAI2010和其他2个不同类型的数据集进行对比实验分析，对比本文模型在不同类型数据集上的分类效果。验证实验数据集信息见表5。

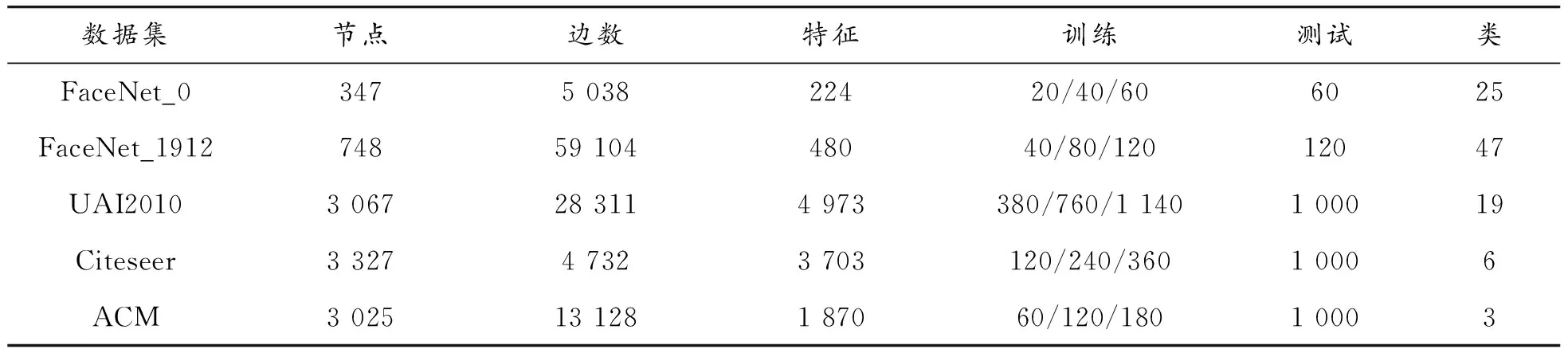
表5 用于模型验证的数据集信息

1) FaceNet_0[20]：Facebook社交网络小子集，节点特征为Facebook用户的性别、生日等属性信息，图由用户间的朋友关系组成，将用户所属的圈子作为类别，所有节点划分为25类。

2) FaceNet_1912[20]：Facebook社交网络小子集，节点特征为Facebook用户的性别、生日等属性信息(与Facebook_0不完全相同)，图由用户间的朋友关系组成，将用户所属的圈子作为类别，所有节点划分为47类。

3) Citeseer[7]：引文网络。节点代表文章，图表示文章之间的引用关系，标签用于识别文章所属的类别，所有节点划分为6类。

4) UAI2010[21]：一个已经在图卷积网络中进行了社区检测测试的数据集，所有节点划分为19类。

5) ACM[22]：从ACM数据集中提取，节点代表文章，特征是文章关键词的词袋表示，图的连边代表两篇论文出自同一作者，所有节点划分为3类。

不同类型的数据集进行节点分类的实验结果见表6。本小节所有对比模型都在相应论文建议的参数基础上进行调优，以求更高的精度。

表6 不同类型数据集实验结果

通过实验结果可以看到：MAIF-GCN在前3个数据集上的分类结果明显优于其他模型，提高1%及以上；MAIF-GCN作用于后2个数据集上时，鲜少有分类精度不变或降低的情况，有的数据集存在较小提升。前3个数据集是社交网络数据集(UAI2010是用于社区探测的数据集，能够归为社交网络一列)，网络存在本文模型引入的2种性质，因此本文模型能够产生效用，从对比实验结果看也的确如此。后2个数据集不属于社交网络范畴，模型引入的2种性质不一定存在于后2种网络，从结果也可以看出，后2个数据集分类精度虽提升却有限，且存在不提升或略有降低的情况，但不提升和降低的情况极少，多数精度仍是提升的。由实验结果分析得出：

1) MAIF-GCN在处理社交网络节点分类的问题上具有积极作用；在不同的社交网络数据集上总能取得较好的效果体现了MAIF-GCN的泛化能力。

2) 其他类型数据集上的分类精度不提升或降低的情况极少，展现了MAIF-GCN的优越性。

4 结论

根据社交网络中存在的同质性和共引规律这2种性质，提取出两类对社交网络中被分类节点产生正向影响的节点：①和被分类节点有着相似属性(相似特征向量)的同质型节点；②和被分类节点链接着较多相同节点(相似领域节点)的共引型节点。分别计算特征向量和邻接矩阵中链接向量的相似程度，选取同质性相似度最高的前k1个节点和共引性相似度最高的前k2个节点，构建两类型节点相应的同质矩阵空间和共引矩阵空间。在构建的2个矩阵空间进行卷积，融合相应类型的节点信息。为了更好地融合各角度提取到的信息，除了单独在矩阵空间进行卷积，还将不同空间卷积的结果相加，通过注意力机制，将提取到的各类型信息进一步融合，最终进行分类，提高分类精度。

本文中提出的MAIF-GCN模型挖掘并融合了相邻节点、同质型节点及共引型节点3种不同类型的关系节点，聚合了邻接邻居、同质最近邻、共引最近邻及三者组合的多角度的信息。在传统社交网络数据集上进行对比实验，MAIF-GCN的分类精度比最先进的分类模型高，证明了提出的两类型节点对社交网络节点分类具有正向影响，证实了MAIF-GCN模型合理有效。