基于隐马尔可夫模型的无侵入疲劳等级判别

尉志礼，胥 川，王雪松，王岳川

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031；3.同济大学 交通运输工程学院，上海 201804；4.道路交通集成优化与安全分析技术国家工程实验室，江苏 无锡 214151)

0 引言

疲劳驾驶是一种危险驾驶行为，会造成驾驶人车辆操纵能力的退化，是引起道路交通事故的重要原因之一[1-2]。根据美国高速公路安全管理局的统计，美国每年大约有328 000起事故由疲劳驾驶引发，造成大约1 090亿美元的损失[3]。美国汽车协会交通安全基金会的调查显示，大约96%的驾驶人认为疲劳驾驶非常危险，但仍有大约24%的驾驶人承认自己每30天会有1次在疲劳状态下进行驾驶的情况[4]。疲劳驾驶是中国高速公路事故的主要原因之一，2015年，中国有8.41%的道路事故和6.21%的高速公路事故由疲劳驾驶导致[5]。近年来，国内外学者对疲劳驾驶的研究关注度越来越高[2]。

目前，交通运输行业对疲劳驾驶相当重视，但是其治理仍然存在困难。在我国，相关法律规定驾驶员连续驾驶4 h后必须进行20 min的休息[6]，相关部门也要求部分客运及货运车辆安装并使用卫星定位系统并接入全国性平台对车辆运行时间进行实时监控[7]。一些公司推出了自己的疲劳监控产品：Volvo在汽车上搭载能够实时监控车辆运动状态的疲劳预警系统[8]；OPTALERT通过无线眼镜检测眼动指标来判断驾驶员疲劳状态并已投入商用[9]。尽管采取了一些措施，但是针对疲劳等级的判别，还需要更加准确可靠的模型[10]。

按照测量设备与驾驶人的额外接触关系，用以判别疲劳等级的测量指标可以分为两种:侵入测量指标(有额外接触测量)和无侵入测量指标(无额外接触测量)。侵入测量指标主要有脑电信号、心电信号和肌电信号等生理信号[11-14]，这类指标具有可靠性强的优点，但是通常通过在驾驶人表面粘贴电极获取数据，容易干扰正常驾驶。此外这类指标的采集和处理需要多种昂贵的设备仪器和复杂的计算方法，特征参数提取时效性较差[1,11]，因此还未广泛应用于实际。无侵入测量指标主要通过对面部特征和车辆运行状态的检测获得，包括眼特征参数、口部特征、头部位置以及车辆运行参数等指标。这些指标的获取方法不会对正常驾驶产生影响，因此具有更好的实际应用前景。

目前，利用无侵入测量指标进行驾驶人疲劳等级判别已有很多研究。Zhang等[5]将疲劳状态分为3个等级，使用车辆运行参数和眼动指标PERCLOS，并考虑时间积累效应，建立了logit模型进行疲劳状态识别，准确度为62.84%；Shahverdy等[15]根据加速度、油门大小、速度和发动机转速来分析驾驶人是否处于疲劳状态；Arefnezhad等[16]进行了模拟驾驶试验，根据车道中心偏移值标准差、横向加速度、横摆角速度、方向盘转角和方向盘转动速率共5个车辆运行特征参数和操作参数建立了三级疲劳等级判别模型，准确度能够达到96%；胥川等[17]基于模拟驾驶试验的数据，计算出了23个无侵入测量指标，经比较发现，闭眼时间比例、平均瞳孔直径、车道偏移标准差、方向盘反转次数是用于疲劳等级判别最重要的指标；Chai等[18]从模拟驾驶试验的数据中设计了11个与方向盘有关的指标，并使用其中和疲劳等级有显著关系的4个指标分别建立了MOL模型、SVM和BP神经网络模型进行对比分析，根据结果认为考虑到个人差异的MOL模型效果最好。

用于对疲劳等级进行判别的模型多种多样，目前常见的模型有k近邻算法[19]、Logit模型[5,17,18,20]、支持向量机[21-23]、神经网络[15,16,24,25]等。由于驾驶人的疲劳状态不能被直接观察到，并且单一无侵入测量指标和疲劳程度的相关性不高[26]，给无侵入疲劳检测带来一定困难。而本研究所使用的隐马尔可夫模型(hidden Markov model，HMM)由于其双重随机性的特征，能够在可观测状态和隐含状态之间建立联系，同时该模型兼顾到了驾驶疲劳是随时间变化的动态随机过程。此外，相比于人工神经网络等研究方法，HMM由于具有良好的监控性能以及诊断效果，学习过程需要的数据样本量更小，因此将其作为疲劳等级判别模型值得尝试[27]。

Fu等[13]使用实车进行试验，根据获取的EEG、EMG等侵入测量指标的数据建立了动态HMM，并证明了该模型用于疲劳等级判别行之有效；Liu等[14]将疲劳状态划分为了3个等级，使用EEG等生理指标建立了KPCA-HMM复合模型，最终模型的识别准确度为84%，同样他们也认为HMM是用于判别疲劳等级的有效模型。目前使用HMM进行疲劳等级判别的研究中，大多都使用侵入测量指标进行输入[12-14,28]，而使用无侵入测量指标建立隐马尔可夫模型进行疲劳等级判别的研究较少。

本研究通过高仿真度驾驶模拟器进行了模拟驾驶试验，采集了驾驶行为数据、眼动信号和主观疲劳数据，根据这些数据提取出了4个无侵入测量指标，结合能够反映驾驶累计时间的驾驶圈数，将疲劳状态分为3个等级，建立了疲劳分级隐马尔可夫模型对疲劳等级进行判别，使用交叉验证的方式得到了模型的判别准确度，并建立了支持向量机用以对比。

1 试验方法

1.1 试验设备

试验采用如图1所示的同济大学高仿真度驾驶模拟器。该模拟器可实现八自由度驾驶仿真，模拟舱内含有一台专用的梅甘娜3系轿车，并安装了一些必要的传感器和音响系统，试验时与驾驶实车的操作基本相同。驾驶过程中的视觉信息主要通过柱面沉浸式投影系统和3块模拟后视镜的LED屏幕提供。这套系统的有效性已通过测试，模拟器的仿真度可以满足本研究需要。

图1 高仿真度驾驶模拟试验平台Fig.1 High-fidelity driving simulation experiment platform

同时在试验过程中使用四通道SmartEye眼动仪对眼动信号进行采集，该眼动仪能实现二自由度目光追踪和六自由度头部跟踪。同时配备了4个摄影装置，用于拍摄驾驶人的面部视频，跟踪头部方向。

1.2 驾驶人

驾驶人共12名，年龄最小为22岁，最大为52岁，平均年龄为33.6±7.5岁(平均值±标准差)。所有的受测人员均持有驾照，无精神疾病、睡眠相关疾病，不需要长期服用药物。受测之前24 h内未饮用酒精饮料、咖啡或功能型饮料。

由于本试验主题有关疲劳驾驶，因此需要部分驾驶人在参加试验之前进行预先疲劳生成，分为两种情况。第1种情况要求驾驶人在前一夜整夜不睡觉后，于第2天早上8点进行试验；第2种情况要求驾驶人在前一夜正常睡眠8 h后，在午饭后下午1点进行试验。

1.3 试验场景

模拟驾驶器中的试验道路如图2所示，是一条长为20 km，车道宽为3.75 m，双向六车道的环形郊区高等级高速公路。该道路由6条长2 km的直线路段(路段编号：1，3，5，9，11，13)，8条半径较大的S型曲线(路段编号：2，4，6，8，10，12，14，16)，2条半径为700 m的圆曲线(路段编号：7，15)路段构成。为排除试验道路线形对指标的影响，只对6条直线路段所收集的数据进行处理分析。

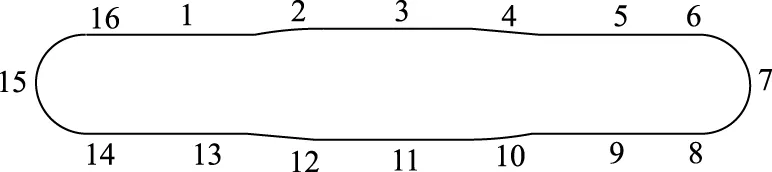
图2 试验道路的线形Fig.2 Alignment of experiment road

驾驶道路两旁设置有一些使人更有真实感的建筑群村落、绿色植物。道路上设置不占试验车辆所行驶车道的交通环境车辆，不设置任何隧道，不安排任何不良天气和环境干扰(如道路横风、雨雪天气)，试验均在白天进行。

1.4 试验步骤

测试前，所有驾驶人需填写驾驶人基本信息调查表和疲劳状态调查表。然后进行5 min模拟驾驶试驾，以提前适应模拟驾驶器的操作。

在试验过程中要求驾驶人将车速保持在120 km/h 左右，全程使用自动挡，并且要求在驾驶车辆过程中遵守交通规则，不进行干扰驾驶的活动，如嚼口香糖、使用手机、听音乐广播、和他人聊天等。行驶到每一圈固定位置时，试验工作人员询问并记录驾驶人的主观疲劳等级(Karolinska sleepiness scale,KSS)。行驶满6圈后终止试验，一次试验历时约1 h。

2 隐马尔可夫模型

2.1 HMM基本假设和结构

隐马尔可夫模型(hidden Markov model，HMM)是能够描述含有隐含状态的马尔可夫过程的统计模型。隐马尔可夫模型与普通马尔可夫过程的区别是状态隐含无法被直接观察到，需要通过可观测状态确定隐含状态的变化过程。

驾驶过程中，驾驶人的疲劳状态是隐含状态，无法被直接观测，而在状态变化过程中驾驶人的各项无侵入测量指标都是可以被观察到的，通过对这些指标的监测和观察，可以推断出驾驶人疲劳状态的变化，符合上述隐马尔可夫模型的特点，因此本研究使用该模型实现对疲劳等级的判别。

隐马尔可夫模型有两个重要假设：

第一，齐次马尔可夫假设。即马尔可夫过程的无后效性，是指驾驶过程中，t+1时刻的疲劳状态概率分布只与t时刻的疲劳状态有关，与t时刻之前的疲劳状态概率分布无关，用公式表达为：

P(qt+1|qt,qt-1,…,q1)=P(qt+1|qt)，

(1)

式中，qt为t时刻下的疲劳状态。

第二，观察独立假设。即t时刻的可观测状态只与t时刻的疲劳状态有关，与之前的疲劳状态和观察值都无关，用公式可以表达为：

P(ot|qt,qt-1,…,q1,ot-1,…,o1)=P(ot|qt)，

(2)

式中，ot为t时刻的可观测状态。

隐马尔可夫模型表示为λ=[N,M,A,B,π]，其中各参数意义如下:

N是指疲劳状态的数量，设N个疲劳状态分别为S1,S2,…,SN，那么qt∈(S1,S2,…,SN)。本研究中驾驶疲劳被划分为3种状态，分别是清醒或轻微疲劳，中度疲劳和严重疲劳，所以N的值为3。

M是指可观测状态的数量，设M个可观测状态分别为V1,V2,…,VM，并记t时刻观察到的状态为ot，那么ot∈(V1,V2,…,VM)。

A为状态转移矩阵，A={aij|i,j=1,2,…,N}，其中：

aij=P(qt+k=Sj|qt=Si)。

(3)

B为观测概率矩阵，是随机变量或随机矢量在各状态的观察概率空间中的分布，可以表示为B=(bjk)N×M，其中：

bjk=P(ot=Vk|qt=Sj)，

(4)

式中，bjk表示在t时刻对应的疲劳状态为Sj时，可观测状态为Vk的概率。

除状态转移矩阵和观测概率矩阵外，还需要确定初始概率分布π。

π为初始概率分布，用于描述在t=1时，即初始时刻各个疲劳状态的出现概率，即π=(π1,π2,…,πN)T，其中：

πi=P(q1=Si),i=1,2,…,N，

(5)

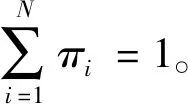
2.2 HMM建模流程与算法

HMM建模流程如下：首先进行试验采集数据，筛选并处理数据后提取指标用以建模。建模时统计疲劳状态和可观测状态来获取模型各项参数值，最后使用交叉验证方式得到模型精度。

本研究中交叉验证具体做法如下：由于训练HMM需要根据试验数据统计得到状态转移矩阵，要求每个驾驶人数据完整，所以按照驾驶人将数据随机分为4组，每组有3位驾驶人的数据。分组完成后，将第1组数据作为测试集计算精确度，其余组的数据作为训练集进行建模；完成1次建模和测试后，将第2组作为测试集，其余各组数据作为训练集进行建模。以此类推，直至完成4次建模和计算，最后取4次判别准确度的平均值来作为模型的整体精确度。

该建模过程需要涉及到以下两个问题和相应算法。

(1)训练问题：已知一个给定的可观测状态序列O=(o1,…,ot,…,oT)，不断地调整模型的参数λ=[N,M,A,B,π]，使该序列的概率P(O|λ)最大，即不断优化参数使模型能够准确地描述该可观测状态的生成方式。

训练问题分两种，疲劳状态和可观测状态值都给出并进行HMM建模的学习是监督学习；只给出可观测状态序列，未给出疲劳状态序列的学习是非监督学习。本研究中的问题属于监督学习，使用统计的方法计算各个参数的初始值,具体公式如下：

(6)

(7)

(8)

(2)解码问题：已知一组可观测状态值的序列O，通过疲劳状态检测模型寻找一个最匹配的疲劳状态序列Q。

解码问题通常使用Viterbi算法进行解决，定义变量：

δt(i)=maxP(o1,…,ot,q1,…,qt-1,qt=Si|λ)，

(9)

式中，δt(i)为t时刻由一组疲劳状态序列q1,…,qt-1,qt且qt=Si推导得到的可观测状态序列。

那么可以推导得到：

δt+1(j)=maxP(o1,…,ot+1,q1,…,qt,

qt+1=Sj|λ)。

(10)

得到递推公式：

(11)

记ψt+1(j)=arg max(δt(i)aij)，表示在t+1时刻疲劳状态为Sj的所有单个状态转移路径中概率最大的转移路径中t时刻的疲劳状态[29]。利用ψt+1(j)即可进行回溯找到生成既定可观测状态序列的概率最大的疲劳状态序列。

3 数据准备

3.1 数据采集

试验过程中采集了以下4大类原始数据：

(1)眼动数据

通过眼动仪所采集的各种信号[30]，如眨眼频率、眨眼时间、闭眼时间、瞳孔直径、眼睑开度等。

(2)操作数据

驾驶人对于车辆的控制数据，如驾驶档位、方向盘角度、刹车踏板力、油门开度等。

(3)车辆运行特征数据

车辆的运行参数数据，如车辆横纵加速度、行驶速度、横向速度、车道偏移值等。

(4)主观疲劳等级

主观疲劳程度量表，即KSS量表,分为9个等级，常用于快速测量疲劳程度，见表1。KSS疲劳等级已经证明和眼动图(EOG)的变化有显著的相关性并且能够有效地反映疲劳对驾驶任务的影响[31]。在试验过程中，驾驶人在每圈的固定位置汇报KSS等级。

表1 主观疲劳程度量表Tab.1 Karolinska sleepiness scale

本研究将驾驶人的疲劳程度分为3个等级[32]：1≤KSS≤6时，驾驶人疲劳状态为清醒或轻微疲劳，记为疲劳等级Ⅰ；KSS=7时，驾驶人疲劳状态为中度疲劳，记为疲劳等级Ⅱ；8≤KSS≤9时，驾驶人疲劳状态为严重疲劳，记为疲劳等级Ⅲ。

KSS是驾驶人主观报告的数据，和实际的疲劳程度可能存在偏差。因此，为提高疲劳程度的准确度，在试验过程中还录制了驾驶人的面部视频。在试验结束后，由经过专门训练的研究人员观看视频，通过对驾驶人的眼睑开度、眼球活动、注意力、反应等对所有驾驶人的KSS进行评定和修正。

3.2 特征参数

本研究需要从试验原始数据中计算眼动和驾驶行为指标并输入进隐马尔可夫模型。眼动指标是对眼动仪采集的数据进行处理后，根据眼动参数计算得出的，主要包括闭眼时间比例(PERCLOS)、平均眨眼时间(Blink_duration)、平均瞳孔直径(Pupil)、平均眨眼频率(Blink_Frequency)等。驾驶行为是指驾驶人操作的数据和车辆运行的特征数据。本研究结合以往的相关研究，从试验原始数据中提取了5个指标，具体的指标和描述见表2。

表2 试验数据中提取出的指标Tab.2 Indicators extracted from experimental data

表2中的驾驶圈数代表驾驶人在试验中处在第几圈，从过往研究可知，疲劳程度会随着驾驶时长加深[5]，故使用该指标。

3.3 数据预处理

为了消除操作不当和仪器误差带来的影响，需要对数据中的异常值进行识别和替换。采用箱线图法进行异常值识别，原理如下：

计算出75%分位数和25%分位数的差值，即四分位差数，记为IQR：

IQR=Q2-Q1，

(12)

式中，Q1为25%分位数；Q2为75%分位数。

以Q2+1.5IQR为上限、Q1-1.5IQR为下限识别异常值，超出上下限的异常值使用该圈下的均值进行替换。在替换完成后重新进行异常值识别和替换，重复进行直至不存在异常值为止。

结果显示，LP_stdev替换了15个异常值，PERCLOS替换了28个异常值，Pupil替换了1个异常值，SWM_Re没有异常值。通过以上分析，最后确认了Round，LP_stdev，PERCLOS，Pupil以及SWM_Re共5个参数作为疲劳等级判别的指标。

4 疲劳分级隐马尔可夫模型

4.1 HMM转移模型的确定

本研究根据KSS将疲劳程度分为了3个等级：清醒或轻微疲劳，中度疲劳以及严重疲劳。为了和疲劳等级相对应，所有的指标参数也应该通过聚类分为3个等级，随后进行组合形成综合观察状态。如果每个指标都分为3个等级，一共有3的5次方，即243个可观测状态，那么隐马尔可夫的观测矩阵就会有243列，而本研究使用的数据一共420条，也就是说观测概率矩阵将会变得非常稀疏，模型的可靠性会受到影响；并且直接使用所有指标无可避免的会受到数据中杂质的影响。因此，本研究在构建隐马尔可夫模型前，先对确定下来的指标使用主成分分析(principal component analysis,PCA)进行降维，降维过后选择前两个主成分进行模糊C均值聚类，每个主成分聚为3类，得到9类综合可观测状态，最终完成HMM的建立。

记重要度最高的2个主成分为C1和C2，2个主成分的组成分别为：

C1=-0.456×Round-0.382×LP_stdev-0.607×

PERCLOS+0.521×Pupil-0.072×SWM_Re

C2=0.063×Round-0.257×LP_stdev+0.323×

PERCLOS+0.368×Pupil+0.831×SWM_Re。

对这2个主成分进行模糊C均值聚类。为了和疲劳等级对应，C1和C2在进行聚类时的类别数选择为3，聚类中心见表3。

表3 C1和C2聚类中心Tab.3 Clustering centers of C1 and C2

由于每一个主成分都有3种状态，因此融合C1、C2这2个主成分后，共有32=9种可观测状态，记为1至9。

在隐马尔可夫模型结构方面，3种疲劳状态之间可以相互转换，此外，同一种状态也能维持不变。根据以上假设可以得到如图3所示的隐马尔可夫模型结构。

图3 疲劳分级隐马尔可夫模型结构Fig.3 Drowsiness classification HMM structure

4.2 隐马尔可夫模型建立

本研究使用了交叉验证的方式来得到模型精度，将12个驾驶人随机平均分成了4组，一共建立4次模型。下面以其中一组作为测试集，其余组作为训练集建模时的模型参数为例进行说明。

进行隐马尔可夫模型的构建时，需要计算出关键性的参数：状态转移矩阵A(由疲劳状态序列得出)、初始状态概率分布π(由疲劳状态序列得出)、观测概率矩阵B(由疲劳状态序列和可观测状态序列得出)。

状态转移概率矩阵A的具体计算方法为统计训练集中驾驶人疲劳等级变化的情况。训练集中共统计到了303次疲劳状态转移的情况，得到的状态转移矩阵如下式所示：

(13)

可以看出，9名驾驶人从清醒或轻微疲劳发生状态转移的总次数为137，在下一次统计状态时，保持该状态不变的次数有130次，所以a11=130/137；而从清醒或轻微疲劳状态转变为中度疲劳状态的次数有7次，所以a12=7/137；没有出现从清醒状态直接转换为严重疲劳状态的情况，所以a13=0。从这3项数据体现出驾驶人在处于清醒或轻微疲劳状态时，大概率会保持这个状态进入下一个路段的驾驶，较低概率进入中度疲劳状态，不会跳过中度疲劳状态直接进入严重疲劳状态。从第2行的数据看出，驾驶人从中度疲劳状态发生状态转移的总数量为128，他们在进入下一圈重新变成清醒状态的次数为1，即a21=1/128；保持该状态进入下一路段的次数为122，所以a22=122/128；从中度疲劳状态进入严重疲劳状态的次数为5，a23=5/128。从第2行的数据体现出，试验者在处于中度疲劳状态时，几乎不会在接下来的路段中转移为清醒或轻微疲劳状态，维持不变的概率最大，转变为严重疲劳状态的概率也较小。驾驶人处于严重疲劳状态的数量有50次，没有出现转换为清醒或轻微疲劳状态的情况，所以a31=0；转换为中度疲劳状态的次数有1次，所以a32=1/50；保持该状态不变的次数为50次，所以a33=49/50。从第3行的数据看出如果驾驶人已经处于严重疲劳状态，那么他们不会在短时间内重新回到清醒或轻微疲劳状态，回到中度疲劳状态的概率也较低，保持该状态进入下一圈测试的概率很大。

根据状态统计，可以计算得出初始状态概率分布π：

(14)

一共观测到324个疲劳状态，其中清醒或轻微疲劳状态占到了138次，以此类推，得到其余两个状态的初始概率分布。

观测概率矩阵B同样使用统计的方法来计算，统计疲劳状态和可观测状态的情况，具体步骤如下：

每一种疲劳状态都对应9种可观测状态，因此原始观测概率矩阵B为:

(15)

根据式(8)计算出B中各元素的值。同样以b11为例，在疲劳等级为Ⅰ(清醒或轻微疲劳)的前提下，可观测状态为1的概率。根据统计，疲劳等级为Ⅰ的总数为138，在疲劳等级为Ⅰ的前提下，可观测状态为1的数目为3，因此b11=3/138，矩阵B中其他元素可以按照同样的方法求出。

观测概率矩阵B为:

(16)

使用R中的“HMM”包进行建模，使用“e1071”包进行聚类，各项指标的预处理也在R中完成。

4.3 模型准确性分析

将测试集中的数据代入训练后的模型，并与实际得到的疲劳等级进行对比和分析。HMM交叉验证的精度见表4。

表4 HMM判别结果Tab.4 Identification result by HMM

从表4中可以看出，预测精度最高的模型为第一组模型，总体预测精度为81.25%。该组模型在进行识别时，误差主要来源于疲劳等级Ⅱ，即驾驶人处于中度疲劳状态时的情况，此时模型会有将状态识别为清醒或轻度疲劳以及严重疲劳的倾向。

从所有结果来看，4组交叉验证的平均精度为77.26%，没有出现当疲劳等级为Ⅲ但预测结果为Ⅰ的情况，即驾驶人的实际疲劳等级为严重疲劳时不会判别为清醒或轻度疲劳。从表4中可以看出一组中的各个疲劳等级的数量并不完全均衡，一定程度上影响了判别精度。

如果去除驾驶圈数这一指标，只使用驾驶行为指标和眼动指标，那么平均正确率只有55.61%，这表明能够反映累计驾驶时间的驾驶圈数是用以判别驾驶疲劳等级的有效指标。值得注意的是，即使去除了驾驶圈数这一指标后，HMM在进行疲劳等级判别时，也并没有出现将严重疲劳误判为清醒或轻微疲劳的情况。

4.4 模型对比

采用SVM，即支持向量机与本研究使用的HMM进行对比。使用同样的驾驶人数据和同样的分组方式进行交叉验证。使用R软件中的“e1071”包进行建模，每次建模都会选择最优的超参数C和γ。模型准确度如表5所示。

表5 SVM判别结果Tab.5 Identification result by SVM

从表5中可以看出，SVM的精度明显低于HMM的精度，并且出现了驾驶人实际疲劳等级为Ⅲ时预测疲劳等级为Ⅰ的情况，4组交叉验证的平均精度为65.02%，同时，如果去除驾驶圈数这一指标，平均正确率会下降到50.46%，再次表明驾驶圈数是用以判别疲劳等级的有效指标。

5 结论

本研究将隐马尔可夫模型应用于驾驶疲劳等级的判别。从模拟驾驶数据中采集了驾驶操作数据、车辆运行数据和眼动数据，并通过主观疲劳程度量表获取了主观疲劳等级数据。从数据中提取了LP_stdev、SWM_Re、PERCLOS和Pupil共4个无侵入测量指标，结合驾驶圈数建立了疲劳分级隐马尔可夫模型，此外，还建立了支持向量机用以对比，得到了以下结论：

(1)无论是HMM还是SVM，引入驾驶圈数都能够提高模型的精度，这表明累计驾驶时间是用以判别疲劳等级的有效指标。

(2)本研究中的疲劳分级隐马尔可夫模型使用4个无侵入指标和能够反映累计驾驶时间的驾驶圈数指标进行疲劳等级判别，不会对正常驾驶造成干扰，相对于使用侵入指标，实用性更强。

(3)当使用无侵入测量指标判别疲劳等级时，疲劳分级隐马尔可夫模型相对于SVM准确度更高，4组交叉验证平均准确度达到了77.26%。

(4)相对于SVM，疲劳分级隐马尔可夫模型判别结果更加稳定，不会出现将严重疲劳状态误判为清醒或轻微疲劳状态的情况。

(5)当用以判别驾驶人疲劳等级的指标增加，综合可观测状态的数量也会随之增多，观测概率矩阵也会变得稀疏，本研究中的疲劳分级隐马尔可夫模型使用了PCA降维有效地解决了这个问题，提升了模型的普适性。

本研究通过驾驶模拟器进行试验，还需要在实车试验中验证结论；驾驶人在限定范围内进行了挑选，后续研究可以把研究范围扩展到其他重点驾驶人群体并增加样本量。除此之外，在试验中需要驾驶人在固定位置接受问询并报告KSS等级，此行为可能会对精神状态有一定干扰，未来可以建立通过面部视频识别驾驶人疲劳等级的可靠标准和体系，直接通过驾驶人面部识别获取其疲劳程度，不再采用问询方式。