基于灰色回归模型的农产品冷链物流需求分析及预测
李思聪,叶 静
(交通运输部公路科学研究院,北京 100088)
0 引言
生鲜农产品是我国冷链物流服务对象的主要品类。目前,国内外关于冷链物流领域的研究多集中在影响因素、供应链优化、服务评价、信息化建设等方面。在冷链物流需求预测方面,定性预测的方法一般包括头脑风暴法、专家意见法、德尔菲法。为了提升冷链物流需求预测精确程度,大多研究采用定量预测方法,比较常见的模型包括多元线性回归、BP神经网络、灰色预测模型、支持向量机以及各类组合模型等方法开展预测。
在多元线性回归模型方面,Hsieh等[1]采用回归预测的方法预测了生鲜农产品冷链物流需求;李隽波等[2]采用多元线性回归模型预测了我国水产品冷链物流市场需求;王新娥等[3]以新疆农产品冷链物流为对象,利用多元线性规模模型开展了预测;梁艳等[4]采用多元线性回归对天津市农产品冷链物流需求进行了预测。在灰色预测模型方面,李夏培[5]以灰色GM(1,1)模型为基础,借助蚁群算法对北京市农产品冷链物流需求进行了预测;杨筝等[6]以广西农产品冷链物流需求为研究对象,利用灰色预测GM(1,1)模型开展了预测;李晔等[7]利用GM(1,1)模型对河南省果蔬冷链需求进行影响因素分析,并开展了需求预测;文先明等[8]考虑需求影响因素,建立GM(1,N)模型对湖南省农产品冷链物流需求进行了预测。在BP神经网络的模型方面,王新利等[9]构建了基于BP神经网络的预测模型,对农产品冷链物流需求进行了预测;兰洪杰等[10]以北京奥运会食品冷链物流市场需求为研究对象,利用神经网络理论建模开展了需求预测。在组合预测模型方面,蒋宇斌等[11]选取针对宁夏冷链物流市场需求预测,采用基于熵权的组合预测法开展了研究;原静[12]对比了采用不同模型进行农产品冷链物流市场需求预测的结果,包括趋势预测、指数平滑、神经网络模型、回归预测和灰色模型等;崔毅等[13]将灰色理论与马尔科夫链相结合,构建了灰色马尔科夫预测模型,对青岛市冷链物流需求进行了预测;李义华等[14]在传统灰色模型基础上,构建了滑动无偏灰色预测模型,对湖南省农产品冷链物流需求进行了预测;王晓平等[15]针对北京生鲜农产品冷链物流市场需求,利用支持向量机模型进行了预测。
综上所述,现有研究尚存在以下不足:一是针对全国层面冷链物流需求预测的研究相对较少,更多需求预测都聚焦在省市范围或某一生鲜品类。随着双循环战略、需求侧改革的深入推进,我国冷链物流行业进入发展快车道,亟待加快开展对全国层面的冷链物流市场需求研究。二是影响因素方面,由于冷链物流行业统计工作起步较晚,大多研究普遍采用社会经济发展和物流业发展方面的统计数据,冷链物流行业数据较少。三是从方法来看,由于冷链物流历史数据较少,市场需求影响因素较多,单一模型均存在一定局限性,急需组合模型的方法创新。如灰色GM(1,1)模型在预测时只考虑了自变量本身的影响,而没有考虑其他外界影响因素对预测结果的影响作用;神经网络模型非线性拟合能力较强,但适用于有大量历史数据的中长期预测。因此,本研究采用灰色模型与多元线性规模相组合的模式对冷链物流市场需求进行分析预测,充分发挥灰色模型和多元线性回归两种模型的各自优势,增强数据规律性,提升变量指标与预测指标的相关程度,起到相互补充和提高模型精度的作用[16]。同时,切合冷链物流行业实际选取预测指标和影响因素指标,利用灰色关联分析研究各类影响因素对预测指标的影响,以期研究结论和建议科学、合理、有操作性。
1 冷链物流需求特征
(1)居民消费促进冷链物流市场需求持续增长
我国人口规模大,民生消费需求基础稳定。近年来,随着城镇化建设的快速推进,城乡居民消费水平不断提升,人们的食品消费不仅注重量的满足,而且追求质的提高,无论是消费质量和消费结构都发生了明显变化,特别是居民食品消费结构中冷冻食品(如冷冻水产品、速冻食品、冷冻饮品等)、低温乳制品的占比显著增加。居民越来越关注和重视食品安全问题,带动食品冷链物流市场需求的持续增长。
(2)层次化消费支撑冷链物流市场需求多元化
当前,我国消费需求的变化不仅是“量”的增长、“质”的提升,而且展现出层次化、群体化的特征,即不同社会阶层、不同消费群体,其消费需求和消费习惯存在差异,低档消费和高档消费、批量式消费和碎片化消费等多层次需求共存。比如中高收入群体更加追求品牌和质量,愿意以更高的价格购买全程冷链、品质更优的食品,但低收入群体则更关注食品的基本功能,加之对全程冷链物流食品的认知不足,因此更倾向于性价比高的食品。
(3)电商背景下生鲜冷链物流需求爆发式增长
互联网时代,居民消费行为与生活方式都发生了巨大改变。随着电商新零售模式的快速发展,线上线下加快融合,衍生出多元化、多样化的履约模式、流通模式和消费场景,生鲜电商、零售O2O、餐饮外卖、社团生鲜等新型流通业态不断涌现,尤其是新冠病毒肺炎疫情发生后,加速了线上购物、网上订餐等“宅经济”的活跃发展,社区菜市场、生鲜便利店、超市等末端生活服务节点生鲜配送需求上升,生鲜冷链物流需求随即井喷。
2 研究方法与指标构建
2.1 研究方法
2.1.1 灰色关联分析
灰色关联分析法是根据因素之间发展态势的相似或相异程度来衡量因素间关联的程度,能够揭示事物动态关联的特征与程度[17]。
经过预处理的母序列记作Y0,子序列分别为X1,X2,…,Xi,计算P=|Y0-Xi|,关联系数计算公式如下:
(1)
式中,ρ为分辨系数,ρ越小分辨力越大,一般ρ取(0,1),通常ρ=0.5。最后计算子序列与母序列的关联度,计算公式如下:
(2)
根据各因素的关联度排序,关联度的值越大,说明影响程度越大。
2.1.2 多元线性回归模型
多元线性回归一般通过对2个及以上自变量与因变量进行相关分析建立预测模型,模型表示为:
Y=β0+β1X1+β2X2+…+βnXn
(3)
式中,Y为因变量,Xi(i=1,2,…,n)为自变量,β0为常数项,βi(i=1,2,…,n)为回归系数。
2.1.3 灰色GM(1,1)模型
灰色GM(1,1)模型的预测原理是对某一数据序列用累加的方式生成一组趋势明显的新数据序列,按照新数据序列的增长趋势建立模型进行预测,然后再用累减的方法进行逆向计算,恢复原始数据序列,得到预测结果[18]。
设x(0)为具有n个数据项的原始数列,即x(0)={x(0)(1),x(0)(2),…,x(0)(n)}。
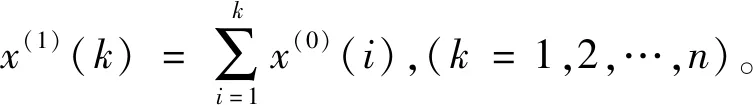
生成x(1)的紧邻均值数列z(1)={z(1)(2),z(1)(3),…,z(1)(k)},k=2,3,…,n,其中z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),k=2,3,…,n。
根据灰色理论对x(1)建立关于t的白化一阶一元微分方程GM(1,1):
(4)
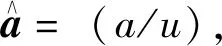
对累加生成数据做均值生成B与常数项向量Yn:
(5)
(6)
(7)
将上述结果累减还原得到预测值:
(8)
2.2 指标构建
2.2.1 预测指标
为了科学准确地预测冷链物流市场需求总量及需求变化趋势,预测指标选取应与冷链物流之间存在很强的相关性,才能使得预测结果更加精确且符合实际情况。此外,设计预测指标应该具有可操作性、可获得性和准确性。
目前,我国冷链物流市场需求指标设计大多采用两种方式。一是从生产端来看,以统计年鉴中果蔬、肉类、水产品等主要生鲜产品产量为基础,分别乘以各类生鲜产品的冷链流通率数据后进行加总,估算我国冷链物流的市场需求[19]。二是从消费端来看,采用人均生鲜产品消费量乘以人口规模来进行计算。由于目前我国产地冷链基础设施建设滞后,生鲜农产品产地损耗严重,冷链流通率在数据获取、准确性、持续性方面都存在较大难度,因此本研究采用第2种方法,即分别统计我国主要生鲜农产品人均消费量,加总后再乘以人口规模作为冷链物流市场需求的表征和预测指标。
2.2.2 影响因素指标
农产品冷链物流是指果蔬、肉类、水产等生鲜农产品从生产、贮藏、运输、销售,到消费的全链条各环节始终处于规定的低温环境的一项系统工程,需求影响因素广泛且复杂,包括农产品供给、社会经济、居民消费、物流业规模等方面。农产品供给是冷链物流的基础,主要代表指标包括生鲜农产品产量、农产品价格、农产品市场成交量等。社会经济发展对冷链物流发展具有重要的促进作用,主要指标包括国内生产总值、人均国内生产总值、第三产业增加值、第三产业对GDP贡献率、商贸流通总额等。居民消费水平代表了购买能力,影响生鲜产品消费。衡量居民消费水平的经济指标一般包括居民可支配收入、居民人均消费支出、居民家庭恩格尔系数、生鲜食品零售额等。物流行业规模因素包括货物运输量、全社会物流总费用、冷链运输车辆保有量、冷库保有量等。考虑影响因素指标的独立性,将从四大维度选取我国冷链物流需求影响因素指标。
3 实证分析
3.1 数据选取
本研究选取我国2001年到2020年的相关指标数据作为样本来进行全国农产品冷链物流需求预测。预测指标为我国农产品冷链物流市场需求总量Y,影响因素指标包括主要生鲜农产品产量X1、农产品生产价格指数X2、人均国内生产总值X3、第三产业对GDP的贡献率X4、城镇居民人均可支配收入X5、冷藏车保有量X6。各指标统计数据如表1所示。
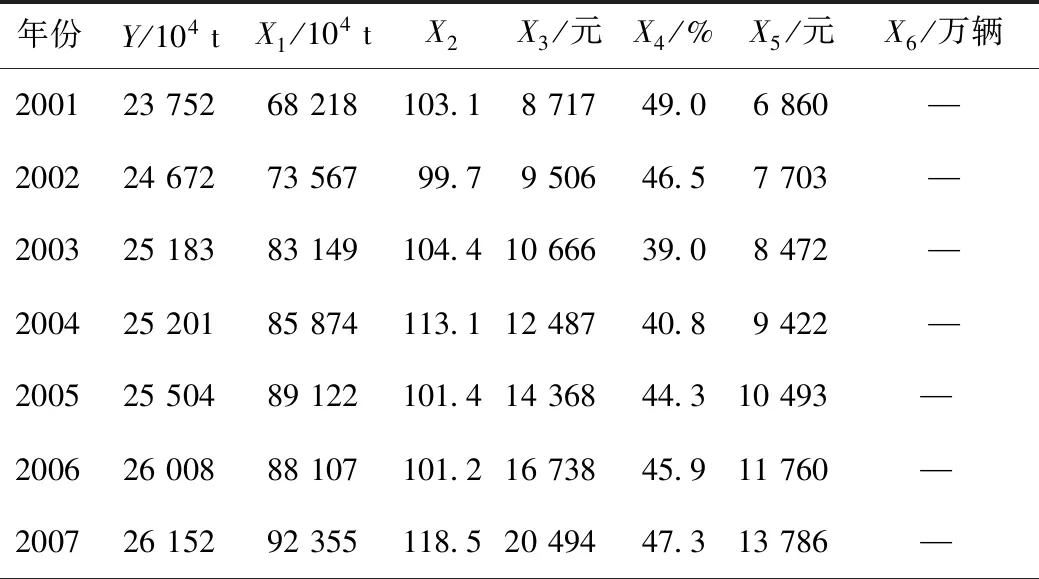
表1 2001—2020年我国冷链物流需求总量及影响因素指标统计Tab.1 Statistics of total demand and influencing factors of cold chain logistics in China from 2001 to 2020

续表1
3.2 实证分析
3.2.1 灰色关联系数计算
由于各数据项在单位上不一致,为保证预测体系数量级与影响因素的数量级一致,采用初值化方法对数据进行无量纲化处理[8],消除因单位不统一而引起的误差,处理后数据列表如表2所示。

表2 我国冷链物流需求指标无量纲化处理结果Tab.2 Dimensionless processing result of Chinese cold chain logistics demand indicators
在使得所有数据均处在相同数量级后,针对6个评价项以及2001—2020年共20年数据进行灰色关联度分析,以冷链物流市场需求总量作为母序列,研究6个评价项与冷链物流市场需求总量之间的关联关系(关联度),分辨系数取0.5,计算灰色关联系数和关联度分别如表3和表4所示。

表3 灰色关联系数Tab.3 Grey correlation coefficients
根据上表关联系数计算灰色关联度r(Y,Xi)。关联度结果如表4所示。
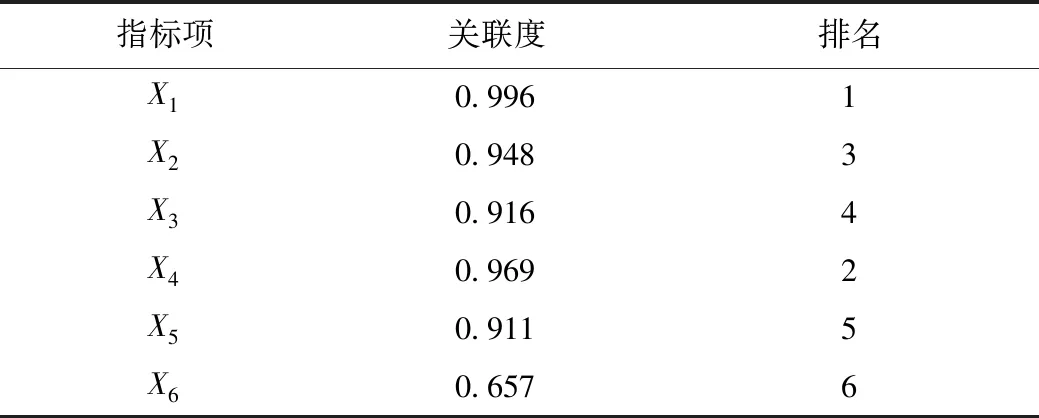
表4 灰色关联度Tab.4 Grey correlation degrees
根据以上灰色关联度值的大小对其进行排序,即可得灰色关联序列为:r(Y,X1)>r(Y,X4)>r(Y,X2)>r(Y,X3)>r(Y,X5)>r(Y,X6),一般关联度大于0.6可以被接受,因此6个指标项与冷链物流市场需求总量均存在较强的关联关系[20]。其中,主要生鲜农产品产量X1与冷链物流市场需求总量Y的关联度最强,其次是第三产业对GDP的贡献率X4、农产品生产价格指数X2、人均国内生产总值X3和城镇居民人均可支配收入X5,关联度均超过0.9,最后是冷藏车保有量X6,与冷链物流市场需求总量Y的关联度值为0.657。
3.2.2 多元回归建模
根据灰色关联分析结论,6个影响因素指标与冷链物流市场需求总量均有较强的关联关系,因此将主要生鲜农产品产量X1、农产品生产价格指数X2、人均国内生产总值X3、第三产业对GDP的贡献率X4、城镇居民人均可支配收入X5、冷藏车保有量X6纳入回归模型。建立我国农产品冷链物流市场需求总量的多元回归初始模型并求解,得到模型系数如表5所示。
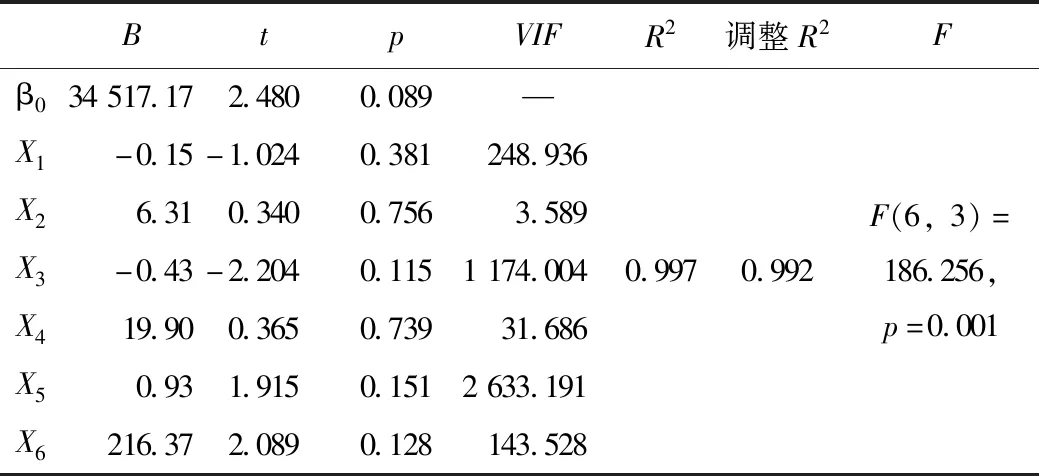
表5 模型系数表Tab.5 Model coefficients
将Y作为因变量,将X1~X6作为自变量进行线性回归分析,可得调整R2=0.992,F检验为0.001<0.05,模型通过拟合系数和F检验。但是模型自变量的显著性检验值都大于0.05,VIF值大于10,存在多重共线性问题,因此采用逐步回归对变量进行筛选,剔除掉相关关系紧密的自变量,提高模型的预测效果。分析结果显示X1,X2,X3,X5均被模型剔除,X4,X6留在模型中。通过逐步回归建立了由自变量X4(第三产业对GDP贡献率)、自变量X6(冷藏车保有量)构建的模型,见图1,得出模型系数如表6所示。

图1 逐步回归模型Fig.1 Stepwise regression model

表6 逐步回归模型系数Tab.6 Coefficients of stepwise regression model
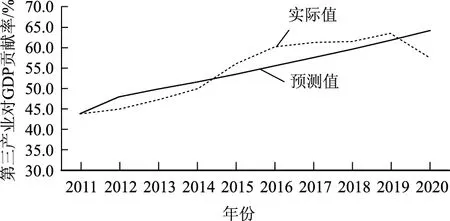
回归模型的可决系数R2为0.991,说明冷链物流市场需求总量变化的99.1%可由第三产业对GDP贡献率、冷藏车保有量的变化来解释,调整可决系数R2=0.988,模型具有较好的拟合优度,并通过F检验(F=373.950,p=0.000<0.05)。DW值为2.143,对比DW检验表,dL=0.697,du=1.641,1.641 因此,建立多元线性回归方程为: Y=22 731.17+238.21×X6+69.50×X4。 (9) 3.2.3 自变量灰预测 通过灰色关联分析以及多元回归模型建立,对自变量X4(第三产业对GDP贡献率)和X6(冷藏车保有量)建立灰色微分GM(1,1)模型进行预测[21]。 (1)X4(第三产业对GDP贡献率)预测 通过对X4进行GM(1,1)模型构建,计算级比值如表7所示,级比检验值均在标准范围区间[0.834,1.199]内,数据适合进行GM(1,1)模型构建。 表7 GM(1,1)模型级比值Tab.7 GM(1,1) model level ratios 模型构建后用最小二乘法求解灰参数,得到发展系数a=-0.036 1,灰色作用量u=45.572 7,后验差比C值0.224 6≤0.35,说明模型精度等级较高。将灰参数带入构建关于t的白化形式的一阶一元微分方程GM(1,1): (10) 通过对方程求解可得: (11) 将上述结果累减还原得到预测值如表8所示,实际值与预测值对比如图2所示。根据预测值对相对误差进行分析,验证模型效果情况。计算得出模型相对误差值最大值0.119<0.2,级比偏差最大值0.074<0.1,模型拟合效果达到要求。 表8 2021—2025模型预测值Tab.8 Model predicted values of 2021-2025 图2 实际值与预测值对比Fig.2 Comparison between actual value and predicted value (2)X6(冷藏车保有量)预测 通过对X6进行GM(1,1)模型构建,计算级比值如表9所示,级比值的最小值为0.727,在适用范围区间[0.834,1.199]之外,说明数据进行GM(1,1)可能得不到满意的模型,但由于偏差不大,可进一步建模以待验证。 表9 GM(1,1)模型级比值Tab.9 GM(1,1) model level ratios 模型构建后用最小二乘法求解灰参数,得到发展系数a=-0.227 1,灰色作用量u=3.308 2,以及后验差比C值;后验差比C值0.003 0≤0.35,说明模型精度等级达到一级水平。将灰参数带入构建关于t的白化形式的一阶一元微分方程GM(1,1): (12) 通过对方程求解可得: (13) 将上述结果累减还原得到预测值如表10所示,实际值与预测值对比如图3所示。根据预测值对相对误差进行分析,验证模型效果情况。计算得出模型相对误差值最大值0.108<0.2,平均相对误差为3.47%,级比偏差最大值0.086<0.1,拟合效果达到较高要求。 表10 2021—2025模型预测值Tab.10 Model predicted values of 2021-2025 图3 实际值与预测值对比Fig.3 Comparison between actual value and predicted value 3.2.4 因变量预测 根据构建的灰色-回归模型,将GM(1,1)模型自变量预测数据带入多元线性回归模型,对2021—2025年我国冷链物流市场需求总量进行预测,预测值如表11所示,实际值与预测值对比如图4所示。 表11 未来5年我国冷链物流市场需求总量预测Tab.11 Predicted total demand of Chinese cold chain logistics market in the next 5 years 图4 实际值与预测值对比Fig.4 Comparison between actual value and predicted value 对因变量Y(冷链物流市场需求总量)直接建立灰色微分GM(1,1)模型,序列级比检验值在标准范围区间[0.909,1.100]内,采用最小二乘法求解灰参数,得到发展系数a=-0.015 8,灰色作用量u=2 340.333 0,后验差比C值0.092 2≤0.35,模型精度达到一级水平。将灰参数带入构建关于t的白化形式的一阶一元微分方程GM(1,1): (14) 通过对方程求解并取得预测值,计算模型相对误差值最大值0.055,平均相对误差值为2.01%,级比偏差最大值0.030,模型拟合效果达到要求。 同时,如采用单一多元线性回归模型平均相对误差为1.71%,灰色—回归模型求得的因变量预测值平均相对误差仅为0.82%。因此相比于单一灰色预测模型或多元线性回归模型,利用灰色-回归模型具有更好的精度和拟合度。 本研究利用我国冷链物流需求相关数据建立了灰色-回归预测模型。分析结果显示,未来5年我国冷链物流市场需求仍呈明显的上升趋势,增速在6%~9%左右,需求规模总体较大。随着国家《“十四五”冷链物流发展规划》出台[21]以及相关配套法规政策的颁布实施,设施设备保有量将进一步扩大,冷链流通率进一步提升,冷链物流行业仍具有较大的发展空间。从预测结果可以看出,模型对我国农产品冷链物流需求总量的中短期预测具有较高的可信度,模型的精准度较高。为适应冷链物流市场需求,更好地促进我国冷链物流高质量发展,提出以下3点建议: (1)加快补齐生鲜农产品“最初一公里”供给短板 农产品供给是冷链物流市场需求最为重要的影响因素,但长期以来由于我国生鲜农产品产地冷链设施设备供给不足,田间地头冷链设施供给不足总量的10%,造成我国生鲜农产品损耗率大、流通效率低。据统计,我国1/3的蔬菜和1/4的水果浪费,主要原因在于产地未及时预冷存储,应围绕果蔬、水产、肉类等农产品主产区,加大产地冷链物流设备供应和设施建设,提升产区“最初一公里”冷链物流服务能力,畅通生鲜农产品上行“最初一公里”。 (2)加强冷藏保温车辆等设施设备有效供给 分析显示冷藏车保有量等设备供给对冷链物流市场需求产生显著的正向影响。近年来我国冷库保有量、冷藏车保有量呈现加速增长态势,年均增速分别超过10%和20%[22],但与发达国家相比人均保有量处于较低水平,人均冷藏车保有量仅为日本等发达国家人均保有量的1/11。在双循环战略背景下,应进一步加大设施设备有效供给,提升设施设备专业化、现代化、智能化水平,持续撬动供给端升级,刺激冷链物流市场需求加速释放。 (3)加大冷链物流市场主体培育力度 以发展第三方冷链物流服务业为重点,加快培育第三方冷链物流龙头企业,提升市场主体集约化、规模化运作水平,增强市场主体信息化运作和网络化服务能力,推动冷链物流与上下游资源整合和信息共享,促进全链条协同发展,打通生鲜农产品流通渠道,连通供给侧和需求侧,畅通国内生鲜农产品大循环。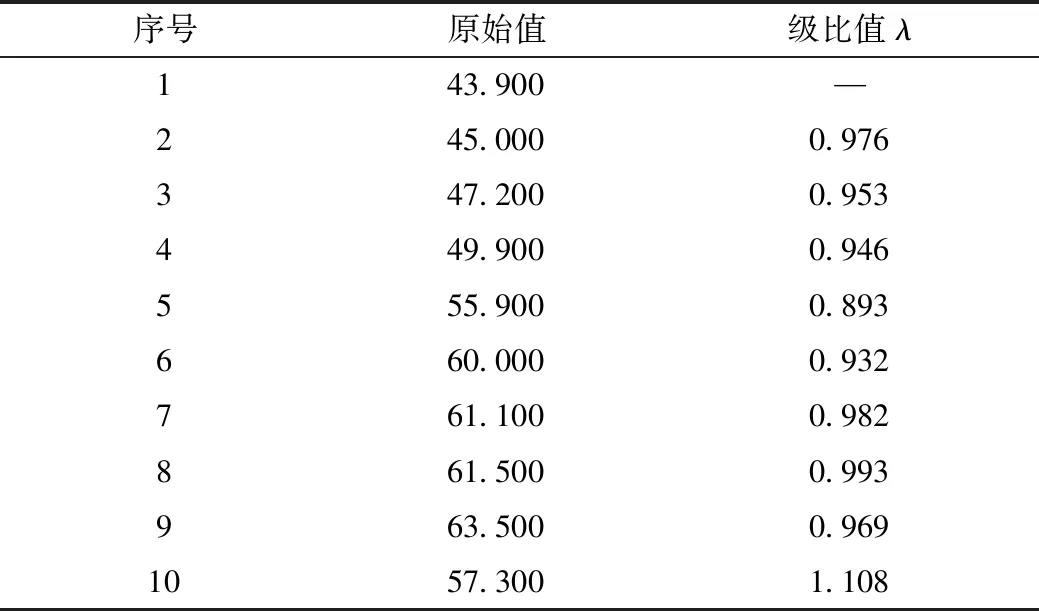






3.3 模型对比
4 结论

