弹簧式衰减器的三维UDF数值模拟分析

辛 清， 张永祥， 李加伟, 张育卿

(海军工程大学 动力工程学院，武汉 430033)

随着现代工业的高速发展，管路被广泛用于船舶海洋工程、大型重装设备以及天然气、油液等输送管道。然而，由管路压力脉动诱发的管路振动和噪声不仅对管路的寿命和安全造成一定的影响，严重时甚至会造成巨大的财产损失和人员伤亡，因此，研究脉动衰减成为国内外学者关注的重点[1]。

为了避免管路压力脉动带来的危害，国内外学者不断寻求降低压力脉动的方法，其中，在管路系统安装压力脉动衰减器是比较有效的方法，并取得了一定的成果，目前普遍采用被动式的压力脉动衰减器来降低管路的脉动[2]。H型(Helmholtz)衰减器，容腔可视为弹簧，颈部可视为质量块，组成一个质量弹簧振动系统，通过谐振产生的反相波，来衰减一定频率范围内的脉动，H型衰减器结构简单可靠，获得了广泛的应用。早在1871年，Baldwin[3]开始着手式压力脉动衰减器的研究。Stein[4]利用电路原理与流体系统的类比，制成类似于换热器中螺旋管道的通道，使流体通过此通道以获得流体脉动的衰减，可有效衰减压力脉动。Stewart[5-7]提出将滤波器的理论应用于压力波动衰减器的研究，采用传递函数和波动法研究不同结构的衰减器衰减效果，为衰减器的研究提供了思路。Tang[8]研究发现利用锥形颈部能够提高H型衰减器的衰减效果，且随着锥形颈部的加长，衰减效果越来越好，但是并没有提出了相应的声学预测公式；为了适应频率的变化，Little[9]提出改变颈部截面以实现调频的半主动式共振衰减器；Lamancusa[10]则通过改变共振腔的体积实现频率的改变，上述理论方法能够实现对衰减器固有频率的调节，但在实际应用中，此类调频方法比较麻烦，在工程应用中存在困难。焦生杰等[11]对H型压力脉动衰减器进行理论分析，建立了衰减器的动态响应模型，研究了H型液压滤波器各参数对衰减效果的影响，研究表明，衰减器体积越大，则阻抗越小，衰减效果越好。曾祥荣等[12]运用集中参数法，研究了H型多孔同心式脉动衰减器的特性，合理选择衰减器结构参数，能够实现衰减给定频率范围内的脉动，拓宽了H型衰减的工作频宽，章寅[13]提出负载大小以及上游管道长度都对其衰减特性有较大影响，集中参数法能够合理求得衰减器的固有频率，但却无法对于衰减器的衰减效果进行量化。Kojima等[14]介绍了一种多自由度串联H型脉动衰减器，其能工作于多个频率范围内，但是这种衰减器一个结构参数会同时影响多个谐振频率，设计具有一定的困难。Selamet等[15-17]研究了不同颈部入口形式对H型衰减器衰减效果的影响，研究表明，通过调整颈部延伸长度、收缩和扩张颈部以及偏置颈部都可以调节H型衰减器的固有频率，有助于设计出更紧凑的衰减器。Mikota等[18]设计了一种由弹簧和质量块组成的紧凑型脉动衰减器，并推导其谐振频率，但其忽略了弹簧运动对流体的影响。

从以往对H型脉动衰减器的研究可以看出，对衰减器的作用机理研究比较清楚，但是在研究过程中忽略了衰减器结构与流体介质的耦合作用，始终难以对衰减器的衰减性能进行定量分析，并且存在工作频率范围较小，体积大的问题。本文基于H型衰减器工作原理的基础上，提出了新型弹簧式衰减器结构，将液压油缸加装弹簧后改装成弹簧式压力脉动衰减器，采用三维UDF数值方法、运用动网格技术对活塞的运动过程进行模拟，实时监测衰减器内部流场变化情况，并分析其衰减性能。

1 衰减器简化模型与工作原理

本文所研究的衰减器结构(如图1所示)与H型衰减器结构一致，是在液压油缸的基础上加装弹簧形成的。与H型衰减器相比，弹簧式衰减器用机械弹簧代替H型衰减器中的流体，机械弹簧与流体共同作用在活塞上，在实际工程应用中可以根据不同的工况，设计使用不同刚度的机械弹簧，以达到最佳的衰减效果。

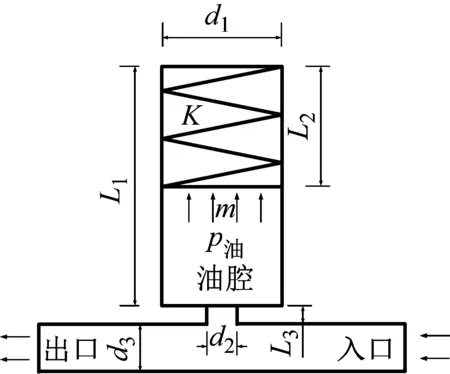
图1 弹簧式衰减器结构简图Fig.1 Structure diagram of spring attenuator

当压力波传到衰减器时，衰减器内液柱在脉动压力的作用下，像活塞一样往复运动，运动的液柱具有一定的质量，再加上管道的阻尼作用，削弱了管路中的压力脉动；另外，活塞在流体压力与弹簧弹力的共同作用做往复运动，当流体压力高于弹簧弹力时，流体推动活塞压缩弹簧，脉动流体多余的能量转化为弹簧弹性势能储存；当流体压力低于弹簧弹力时，弹簧对流体做功，将弹簧弹性势能转化为流体动能，如此以来，不仅提高了能量的利用率，而且能够有效的降低了脉动流体的波动情况。根据衰减器的工作原理，充分考虑质量-弹簧系统的振动特性，通过选用合适的弹簧，使在其谐振频率附近工作，利用质量-弹簧系统的谐振来增强其脉动衰减能力。

2 弹簧式衰减器三维UDF仿真分析

2.1 三维几何模型

根据弹簧式衰减器的结构简图进行建模(如图2所示)，从建模的三维图形可以看出，弹簧式衰减器的简化模型相对简单，其拓扑结构比较规则；活塞在流体与弹簧的共同作用下不断运动，活塞周围伴随网格生成与销毁，对网格质量有着较高的要求，因此采用结构网格对模型进行划分。其优点是生成速度快、网格质量好，与实际模型更为接近，可以实现与区域边界实现较好的拟合，并且节点定义在每一层的网格线上，数据结构简单，节省了计算资源。在划分网格时，为了获得与管路以及衰减器几何拓扑相一致的块结构，对块进行切分，将整体的六面体块分成了三个部分的Block块，并对结构中的圆弧部分进行O型剖分(O—Block)， 充分考虑网格质量与计算成本的前提下，设置网格最大尺寸为4 mm，并对局部网格进行加密处理，划分后的网格数量为62 856，局部网格如图2所示。

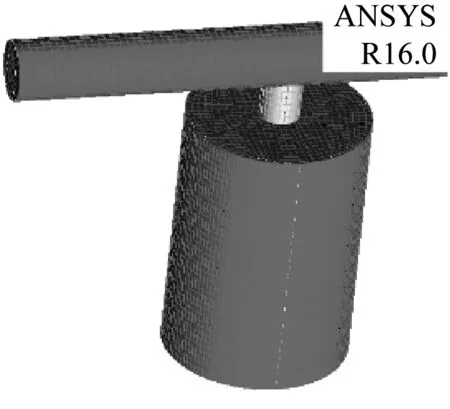
(b) 局部网格图2 衰减器三维几何模型Fig.2 Three-dimensional geometric model of attenuator

2.2 三维UDF数值模拟

本文对弹簧式衰减器的模拟中，重点是采用动网格技术对活塞运动的模拟仿真，动网格技术中的难点是对运动区域的控制以及避免负体积的出现。从图1可以看出，活塞的运动受到流体与弹簧的共同作用，由于流体的压力存在脉动，并且弹簧不断产生形变，因此活塞的受力情况比较复杂，难以采用数学表达式描述，通过编写自定义函数(UDF)的方法，描述活塞与流体的耦合运动。运动的区域包括油缸壁与活塞，油缸壁面做变形运动，设置为Deforming，由cylinder控制其运动过程；活塞在油缸轴向方向做往复运动，Fluent提供的Six DOF模型，不仅可以对刚体在流体压力下的运动进行模拟，而且可以定义活塞质量、弹簧刚度、弹簧预压力，充分考虑重力、弹簧力等外部作用力的影响，可以很方便的限制刚体在某个方向上的自由度，其核心是DEFINE-DOF-MOTION宏，该宏函数的原理是释放油缸轴向的平移自由度，约束其他方向的平移和转动。在仿真过程中，活塞边界会在前面定义的Six DOF模型指定的运动规律下产生刚体平移运动，所以在计算中需要在每个仿真步中根据边界的运动情况，实时更新计算网格，网格更新方式选用动态层法，这种方式计算量较小，并且生成的网格质量高。为了避免负体积的出现导致计算失败，首先给定弹簧一定的预紧力，这样有效的避免了在计算开始的时候，加速度过大，导致负体积出现的问题。

流体介质是46#润滑油，初始温度为40 ℃，密度860 kg/m3，运动黏度46 mm2/s，边界条件如表1。

表1 边界条件设置Tab.1 Boundary conditions setting

仿真的主要目的是模拟流体流经衰减器时对流体脉动的衰减作用，设置入口UDF为不同频率(仿真频率设置如表2)的正弦压力信号，模拟不同频率脉动流体，通过对比出口压力在关闭动网格与打开动网格两种不同状态下的脉动率，分析衰减器在不同工况下对流体脉动的衰减作用。为准确测量压力，待系统稳定后，通过观察衰减器的速度矢量图，避开流体回流区域，在出口附近布置测点P(见图2)，从而获得衰减器在该工况下的脉动衰减率。

表2 仿真工况Tab.2 Simulation conditions

2.3 三维UDF计算模型

一般认为，无论多么复杂的湍流运动，非稳态的连续方程和Navier-Stokes方程对于湍流的瞬态运动是适用的，本文忽略流体密度的变化，速度矢量u在x、y和z方向的分量为u、v和w，湍流瞬态控制方程[19]如下

divu=0

(1)

(2)

(3)

(4)

目前数值模拟方法使用最广泛地湍流模型是标准k-ε模型，在标准的k-ε模型中，k和ε是两个基本未知量，与之对应的运输方程为[20]

Gk+Gb-ρε-YM+SK

(5)

(6)

式中：ρ为流体密度；u、v、w为速度矢量在x，y，z方向上的速度分量；μ为流体动力学黏度；μt为湍流黏度；Gk、Gb为湍流能项；C1ε、C2ε、C3ε为经验常量，取值分别为1.44,1.92,0.99；σk、σε为湍流prandtl数，取值为1.0和1.3。

2.4 仿真结果分析

为了考察不同频率下弹簧式衰减器的脉动衰减率，本文定义脉动率和衰减率如下

(7)

(8)

图3显示的是衰减器弹簧刚度设置为867 684、脉动频率为15 Hz时仿真得到的压力响应曲线，分析压力响应曲线可以得出，当关闭动网格时，压力脉动的最大值为774 kPa，压力脉动的最小值为640 kPa，压力脉动的平均值为707 kPa，计算获得压力脉动为19%；当打开动网格时，压力脉动的最大值为744 kPa，压力脉动的最小值为662 kPa，压力脉动的平均值为703 kPa，计算获得压力脉动为11.67%，此时，衰减器的脉动衰减率为38%。同理，图4显示的是脉动频率为70 Hz时仿真得到的压力响应曲线，分析压力响应曲线可以得出，当关闭动网格时，压力脉动的最大值为777 kPa，压力脉动的最小值为648 kPa，压力脉动的平均值为712.5 kPa，计算获得压力脉动为18%；当打开动网格时，压力脉动的最大值为722 kPa，压力脉动的最小值为683 kPa，压力脉动的平均值为702.5 kPa，计算获得压力脉动为5.6%，此时，衰减器的脉动衰减率为69.1%。

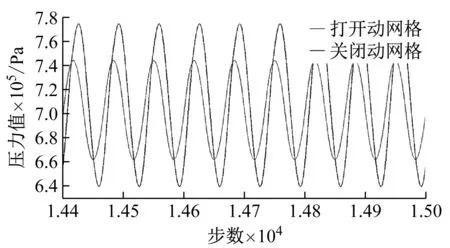
图3 15 Hz时压力响应曲线Fig.3 Pressure response curve at 15 Hz

图4 70 Hz时压力响应曲线Fig.4 Pressure response curve at 70 Hz

(9)

式中：ω为弹簧质量-弹簧系统的谐振频率；k为弹簧的刚度系数；m为弹簧振子的有效质量。

根据式(9)计算衰减器设置四种不同刚度的弹簧时的固有频率如表3。表4显示的是仿真四种不同弹簧刚度的弹簧，在不同频率条件下所获得的脉动衰减率，从表4中可以看出，弹簧刚度以及流体的脉动频率均对衰减效果有着比较明显的影响，其原因是改变弹簧刚度时，衰减器的固有频率随之改变，从而对衰减效果产生比较大的影响；当流体的脉动频率与衰减器的固有频率相同时，衰减器的衰减率可以达到最优，最优的衰减率可达71%，因为此时发生了共振；随着弹簧刚度的降低，衰减谷的宽度不断增大，且刚度减低，有助于衰减效果的提高，有助于拓宽弹簧式衰减器的工作频带。

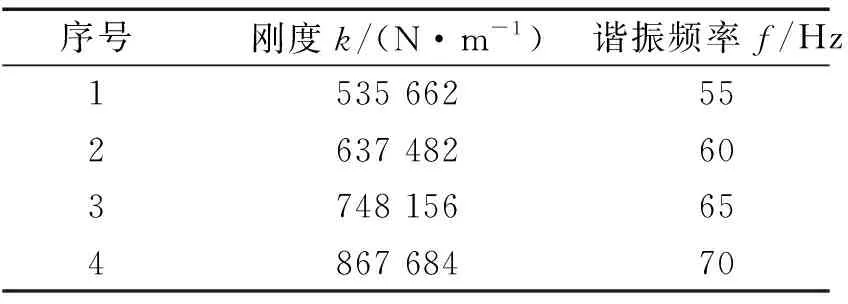
表3 弹簧固有频率Tab.3 Natural frequency of spring

表4 仿真结果Tab.4 Simulation results

3 试验研究

3.1 试验装置及原理

为了验证采用三维UDF数值方法、运用动网格技术对活塞的运动过程进行模拟，计算分析弹簧式衰减器衰减性能方法的正确性和可靠性，根据某柴油机润滑油管路搭建试验平台进行试验研究。试验装置与测点布置如图5所示，该试验平台主要由弹簧式衰减器、双头螺杆泵、油箱、管路、精密压力表以及控制箱等组成，为了准确获得管路内部的压力值，分别选取衰减器

(a) 试验平台

(b) 原理图图5 弹簧式衰减器试验平台及原理图Fig.5 Spring attenuator test platform and schematic diagram

入口与管路系统出口为压力测点，设置压力传感器进行压力信号采集，通过分析不同工况下的压力信号，与仿真信号进行对比，验证本文所提出方法的正确性。

试验原理见图5，试验台工作时，关闭闸阀1，打开闸阀2，润滑油从螺杆泵输出，经循环后通过节流阀3回到油箱，此时，管路系统中无衰减器接入；打开闸阀1、闸阀2，润滑油从螺杆泵输出，油液通过衰减器，经循环后通过节流阀3回到油箱，此时，管路系统中衰减器并联接入。调节节流阀3，使油路达到所需的油压；由控制箱控制螺杆泵的转速，控制润滑油的脉动频率；通过测点1、2压力传感器获得脉动油压的脉动情况。

3.2 试验方案

本文设计的弹簧式衰减器是在MOB 100*400型液压油缸的基础上加装弹簧设计而成的，为了使弹簧式衰减器保持不同的谐振频率，根据无阻尼自由振动系统固有频率的计算公式(式(9))以及弹簧的刚度计算公式(式(10))，充分考虑加工工艺的前提下，设计不同型号的弹簧如表5所示。

(10)

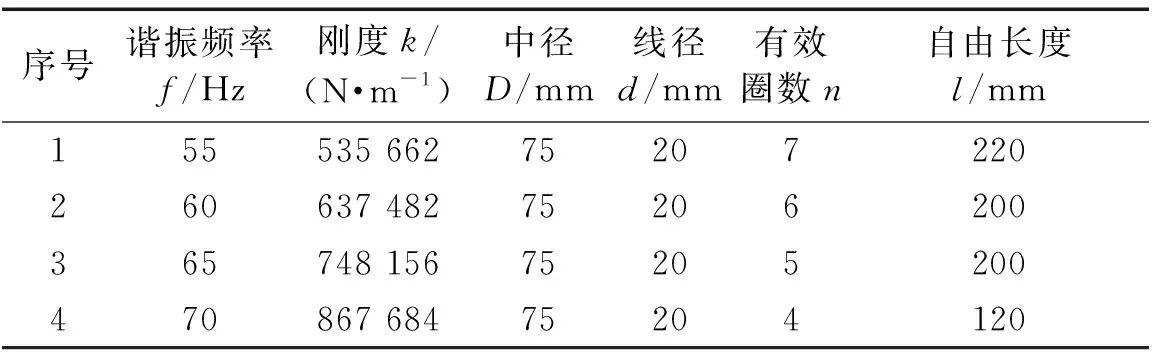
表5 弹簧尺寸Tab.5 Spring size

式中：k为弹簧的刚度系数;G为弹簧材料的切变模量(钢为8×104MPa);d为弹簧线径;C为弹簧的螺旋比;n为弹簧的有效圈数。

选取与仿真模拟相同的工况进行试验研究，工作压力设置为0.7 MPa，管路系统油液脉动频率是双头螺杆泵转频的两倍，转速设置如表6，试验的测试系统主要是由量程为0～3 MPa的HM90-H2-3-V2-F1-W2压力传感器与最高采样频率为131 072 Hz的B&K3610-A-042数据采集器组成，压力传感器的输出端连接B&K公司的PLUSE系统采集器上，传输至计算机，试验时的信号采样频率为16 384 Hz。

表6 试验转速Tab.6 Test speed

3.3 传感器标定

压力传感器在使用过程中由于传感器长时间受地域和时间影响，会产生一些漂移，因此需要对压力传感器进行标定，以降低测量误差对试验的影响。本文参照文献[21]的方法，对测点1、2分别设定特定压力值，并采集输出电压信号，对压力传感器进行手动标定，通过试验建立传感器输入量和输出量之间的关系，标定参数如表7。根据标定参数进行拟合后获得测点1、2传感器的压力测量值与输出电压之间成式(11)、(12)的线性关系。

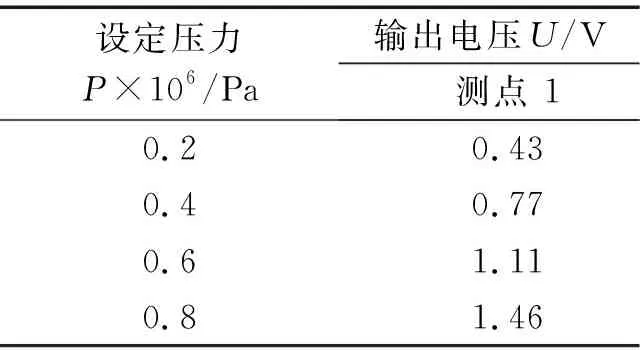
表7 传感器标定数据Tab.7 Sensor calibration datas

Y1=585 470X1-52 459

(11)

Y2=608 640X2+8 295.3

(12)

式中：X为输出电压值；Y为所测压力值。

3.4 试验结果分析

根据传感器的标定，将试验采集的电压信号转化为压力信号，并对试验数据进行滤波处理，获得管路出口附近测点2的时间-压力响应曲线。图6显示的是衰减器安装4号弹簧、螺杆泵转速为450 r/min时采集得到的压力响应曲线，分析压力响应曲线可以得出，不接入衰减器时，压力脉动的最大值为794 kPa，压力脉动的最小值为596 kPa，压力脉动的平均值为681 kPa，计算获得压力脉动为29.1%；接入衰减器时，压力脉动的最大值为750 kPa，压力脉动的最小值为630 kPa，压力脉动的平均值为682 kPa，计算获得压力脉动为17.6%，此时，衰减器的脉动衰减率为39.4%。图7显示的是螺杆泵转速为2 100 r/min时采集得到的压力响应曲线，分析压力响应曲线可以得出，不接入衰减器时，压力脉动的最大值为743 kPa，压力脉动的最小值为552 kPa，压力脉动的平均值为704 kPa，计算获得压力脉动为12.9%；接入衰减器时，压力脉动的最大值为718 kPa，压力脉动的最小值为685 kPa，压力脉动的平均值为703 kPa，计算获得压力脉动为4.6%，此时，衰减器的脉动衰减率为64.4%。

图6 450 r/min时压力响应曲线Fig.6 Pressure response curve at 450 r/min

图7 2 100 r/min时压力响应曲线Fig.7 Pressure response curve at 2 100 r/min

表8显示的是衰减器安装不同刚度的弹簧，通过试验所获得的衰减器在不同转速下的脉动衰减率，从表8中可以看出，在衰减器中安装不同刚度的弹簧，所获得的衰减率是不同的，并且同一弹簧，在不同转速条件下的衰减率也是不同的。由图8可以看出，在衰减器固有频率的附近，衰减器的衰减率可以达到最优，最优的衰减率可达65%；随着弹簧刚度的降低，衰减谷的宽度不断增大，因此降低弹簧刚度，有助于拓宽弹簧式衰减器的工作频带，但是同时也会使得衰减器工作时弹簧的伸缩量将变大，衰减器尺寸变大，将使得弹簧加工难度增加且不利于紧凑型衰减器的设计，同时，伸缩量增大，也不利于衰减器的稳定性，因此弹簧的刚度不能过小。

图8 试验与仿真的结果对比Fig.8 Comparison of test and simulation results

表8 试验结果Tab.8 Test results

从试验与仿真的结果来看，仿真得到的衰减率略高于试验结果，其原因是试验时活塞与油缸壁面存在摩擦，在仿真中并没有考虑；仿真得到的最优衰减率在衰减器固有频率处，而试验得到最优衰减率的频率略低于衰减器的固有频率，原因是在试验中，衰减器充满油液后，导致衰减器的固有频率有所降低。试验结果与仿真结果的平均误差为13%，低于20%，满足一般工程要求，误差在可以接受的范围之内，因此采用三维UDF数值方法、运用动网格技术对活塞的运动过程进行模拟，计算分析弹簧式衰减器的衰减性能的方法是可行的。

4 结 论

本文提出了新型弹簧式衰减器结构，并采用三维UDF数值方法、运用动网格技术对弹簧式衰减器活塞的运动过程进行模拟，对衰减器的衰减性能进行分析研究，得到以下结论：

(1) 仿真结果与试验结果均表明，当流体的脉动频率与衰减器的固有频率一致时，二者发生共振，此时，衰减器衰减效果最好，仿真得到的最优衰减率为71%，试验得到的最优衰减率为65%。当流体的脉动频率偏离衰减器的固有频率时，衰减器的衰减性能下降，因此弹簧式衰减器对频率的选择性有着较高的要求。

(2) 仿真结果与试验结果均表明，弹簧刚度越小，衰减效果越好，衰减器的工作频带越宽，但是低刚度会给弹簧制造带来困难，弹簧尺寸变大，从而使得衰减器体积变大，不利于紧凑型衰减器的设计；低刚度时弹簧的变形量大，不利于系统的稳定。

(3) 仿真结果与试验结果相一致，表明所建立的弹簧式衰减器模型的有效性和研究方法的可行性，为弹簧式衰减器衰减性能的定量分析提供了新方法和新思路。

(4) 通过仿真研究与试验研究发现，本文所提出的弹簧式衰减器对管路内部流体的压力脉动有着明显的衰减作用，能够有效降低管路系统的振动水平，并且可以在不停机的情况下更换弹簧，提高了衰减器的使用灵活性，所提出的弹簧式衰减器结构具有一定的工程意义。