基于不完全信息博弈的动态武器目标分配

姜广胜，史宪铭，陈 静，赵 美，刘昊邦

(1. 陆军工程大学石家庄校区，河北 石家庄 050000；2. 陆军步兵学院石家庄校区，河北 石家庄 050083)

武器目标分配(Weapon Target Assignment，WTA)是作战指挥决策的基础，获得合理、科学的分配策略是打赢现代化战争的关键。为了获得最优的分配策略，国内外学者做了大量研究，其中包括蚁群算法、拍卖算法、粒子群算法等，但大部分把敌方看作无对抗能力的防御对象，仅考虑我方的分配对策，没有考虑敌方的分配对策对我方分配对策产生的影响，忽略了实际作战的动态博弈性。敌我双方的战场态势一直处于变化之中，作战过程实际上就是一场博弈。博弈论是一门完整的科学理论，在古代田忌赛马中就已经灵活运用，在现代也广泛应用于经济、政治、军事等具有竞争性、冲突性和对抗性的领域，其在军事领域,不仅被应用于武器目标分配，还可以应用于无人机编队、舰艇对抗等。

因此，本文充分考虑敌我双方的战场态势变化、毁伤效能评估等因素，以博弈论为基础，建立一种不完全信息的动态武器目标分配模型，并利用遗传算法模拟动态作战过程，缩小决策点范围，有效提高我方武器作战中对未知信息的推理能力。

1 问题描述

合成分队中的武器包括步兵战车、自动炮、坦克等，这些作战力量的价值和打击能力各不相同，由于战场情况瞬息万变，常常包含不确定、动态的复杂因素，敌我双方武器装备的价值和打击能力也随机变化，即各武器装备的价值和打击能力具有随机性和不确定性。因此，作战一方很难获取另外一方武器装备的价值和打击能力等信息，也就是说，敌我双方在作战过程中掌握的信息是不对称的。如何在敌我双方掌握信息不对称的情况下，科学合理地确定我方用哪些武器打击敌方哪些目标的打击方案，以期用最小的打击成本获得最大的毁伤效果是动态武器目标分配要解决的关键问题。因此，利用不完全信息动态博弈模型可以更加合理地对多武器多目标分配问题进行建模，将合成分队的动态武器目标分配问题转化为在不完全信息动态博弈中求解打击策略纳什均衡解的过程。纳什均衡为一个策略组合，是博弈双方的一种均衡状态，通过求解纳什均衡解有助于科学选择打击方案，提高作战效能。

2 模型构建

2.1 矩阵博弈的定义

合成分队的武器目标分配中，将敌我双方分别看作博弈的两个局中人，利用阶段动态博弈展开作战，如图1所示。

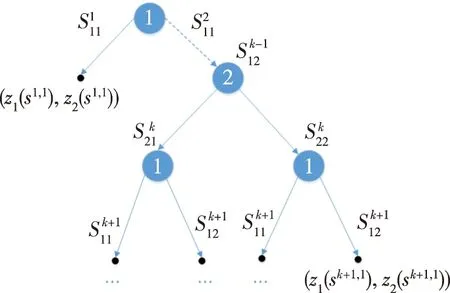
图1 敌我双方k阶段作战动态博弈树

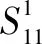
一般情况下，动态博弈包括以下要素：一是局中人，指的是参与博弈的主体，即我方武器和敌方目标；二是策略集，指的是博弈双方有顺序选择的策略集合；三是赢得函数，指的是博弈双方根据选择的策略获得的收益值；四是均衡解，指的是博弈双方最优策略的组合。多武器多目标分配问题可以建模为一个双矩阵博弈模型=(,,)，具体为:

1)={1,2}为博弈中的两个局中人，=1代表我方，=2代表敌方；

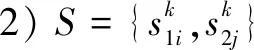
3)=((,),(,))为博弈中两个局中人选择某种行动的支付函数。

2.2 不完全信息

不完全信息指的是博弈的两个局中人没有完全掌握对方的事前信息，另一局中人的策略和选择是不确定的。动态博弈中，我方的目的是在保护自身不被敌方攻击的同时对敌方实施打击，敌方的目的是在保护自身不被我方打击的同时对我方实施攻击，这存在于整个博弈的过程。由于动态博弈存在多变性、随机性等特点，使两个局中人无法掌握博弈中的全部信息，其中，最突出的就是武器目标的杀伤威力不同导致敌我双方的毁伤评估结果具有不完全性，求解最优策略时必须考虑这一因素。

2.3 支付矩阵

由于模型中只存在两个局中人，一个局中人的支付等于另一个局中人的收益，博弈双方的支付和收益的和永远为零，因此可以将模型看作基于不完全信息的两人零和非合作博弈。

假设我方有个武器参与作战，敌方有个目标参与作战，敌我双方武器目标的价值集合分别为和。

={,,…,,…,}

(1)

其中，表示第个武器的价值。

={,,…,,…,}

(2)

其中，表示第个武器的价值。

假设我方的第个武器命中敌方的第个目标的概率为，我方的第个武器被敌方的第个目标命中的概率为，我方的第个武器打击敌方的第个目标的支付值为

=(max)*

(3)

我方的第个武器打击敌方的第个目标、第个武器打击敌方的第个目标的融合支付值为

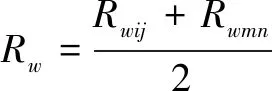
(4)

敌方的第个目标打击我方的第个武器的支付函数为

=(max)*

(5)

敌方的第个目标打击我方的第个武器、敌方的第个目标打击我方的第个武器的融合支付值为

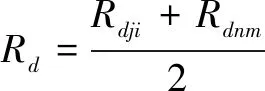
(6)

多武器多目标分配动态博弈的支付函数为

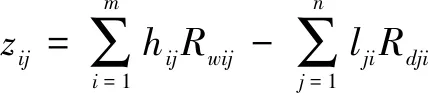
(7)

其中，和都有0、1两个取值。=1代表我方的第个武器打击敌方的第个目标，=0代表我方的第个武器没有打击敌方第个目标；=1代表敌方的第个目标打击我方的第个武器，=0代表敌方的第个目标没有打击我方的第个武器。

根据式(3)和式(5)，可得敌我双方的支付矩阵为。

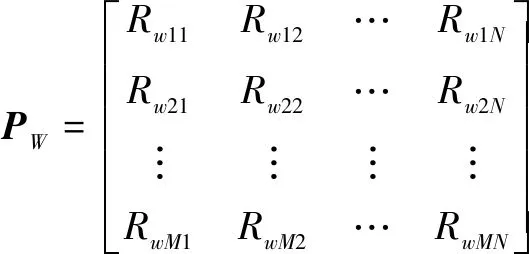
(8)

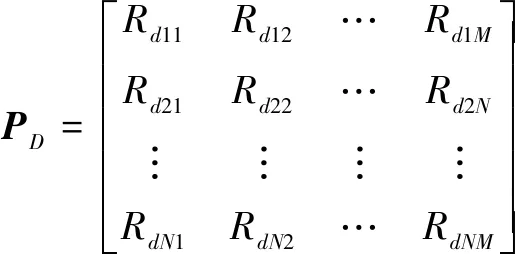
(9)

3 求解方法

3.1 纳什均衡的基本概念及求解方法

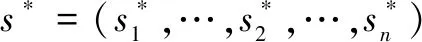
在这个策略组合中，一方的策略都是针对另一方策略的最优反应。

求解纳什均衡解的过程是一项复杂的工程问题，为了提高求解速度，常常借助一些智能算法，比如神经网络算法、粒子群算法和遗传算法等。遗传算法是由Holland提出的一种快速搜索算法，利用生物进化中的编码现象和遗传机制能自动获取和调整搜索空间，具有较好的全局寻优能力，被广泛应用于机器学习、信号处理、打击博弈等问题中。因此，本文在构建多武器多目标分配的博弈模型基础上，利用遗传算法求解纳什均衡。

3.2 遗传算法求解纳什均衡解的步骤

3.2.1 编码

编码主要模仿生物的染色体, 针对最优策略问题, 需要将其变量按照某种编码方式构建一种编码规则，实现由工程问题向遗传问题的转化。根据动态博弈的相关特性，分别对敌我双方的武器目标分配策略进行编码。

我方武器分配策略的编码采用十进制整数编码方式，编码长度为*，染色体编码为()*,其中的约束条件为公式(10)。

≤

(10)

敌方目标分配策略的编码采用二进制编码方式，=1表示第个目标是我方武器的打击对象，=0表示第个目标不是我方武器的打击对象。

3.2.2 适应度函数

针对每个染色体，分别计算到达所有基因位时的支付函数||,找到||最大值所在的基因位，根据基因位的参与者来选择最优策略，若=1，>0，表示选择该染色体对我方有利；若=2，<0，表示选择该染色体对敌方有利。因此，染色体适应度函数可以用支付函数来表示。

3.2.2 交叉

交叉是遗传算法中非常重要的一环，利用交叉可以获得两个群体的新一代个体，新一代个体的特性与父辈的特性息息相关。在武器目标分配问题中，常常采用的是单点交叉方法。

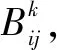
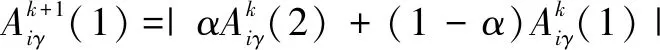
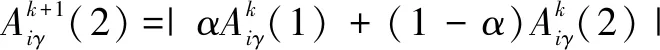
其中，为一个随机常数，取值区间为0≤≤1。

3.2.3 变异

变异是产生新个体的辅助操作，通过设定变异概率可以改变某个或某些个体的基因值，决定算法的局部搜索能力。为了防止算法陷入局部最优的困境，变异概率一般较低，采用单点随机定位的运算来确定。

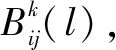
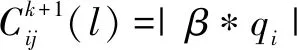
其中，为一个随机常数，取值区间为0≤≤1。

3.2.4 终止策略

如果每个种群迭代的代数均已达到规定的迭代次数，并且某染色体的适应度值在若干代内不再改变，则算法终止，此时适应度值在若干代不再改变的染色体为最优分配方案，即纳什均衡解；否则，继续迭代，直到出现最优解。

3.2.5 求解算法步骤

求解算法步骤详见图2所示。

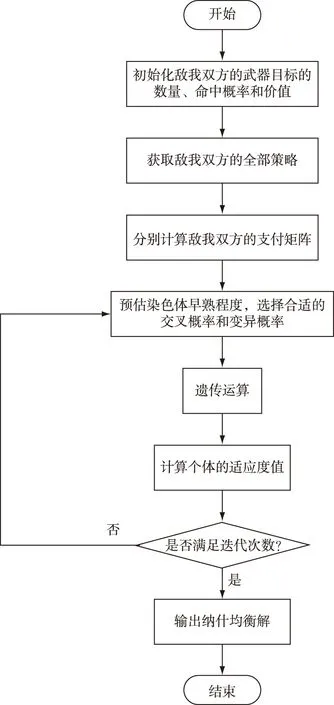
图2 遗传算法求解纳什均衡解的流程图

4 算例分析

为了证明本文提出的基于不完全信息博弈的动态武器目标分配模型及求解算法的有效性，采用案例分析和软件仿真相结合的方式进行验证。

4.1 案例分析

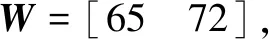
1)={,}，为双矩阵博弈的两个局中人;

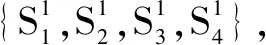
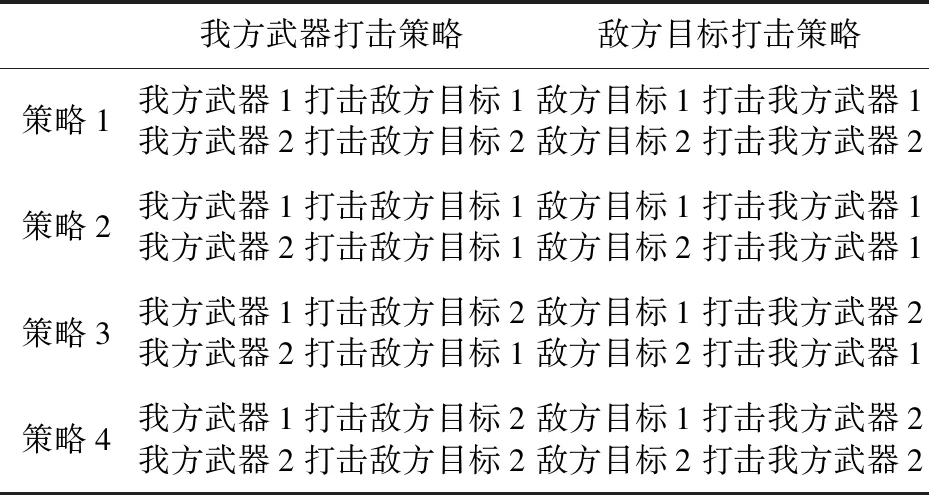
表1 W方和D方武器目标分配的策略集合

表2 敌我双方的策略集合

3)计算敌我双方策略集的支付值，如表3所示。

表3 敌我双方策略集的支付值

4.2 软件仿真

为了验证本文提出的多武器多目标博弈模型的合理性和求解算法的高效性，将遗传算法求解不完全信息博弈纳什均衡的时间与神经网络算法(BP)和粒子群算法(PSO)求解同一模型纳什均衡的时间进行对比，利用软件进行仿真试验。假设敌我双方武器目标数量分别是2、3、4、5、6、7、8、9、10、11个，武器目标的价值={(,),∈(0,100),∈(0,100)} ，打击概率∈(0，1)。借助软件计算不同作战规模下三种算法求解纳什均衡解的时间，如表4所示。

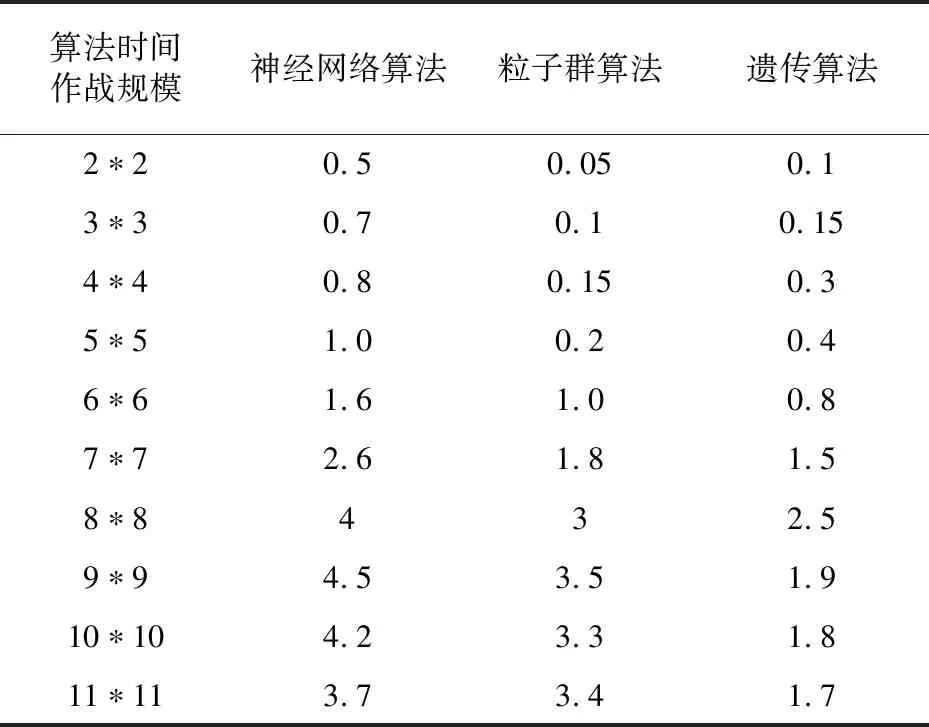
表4 求解纳什均衡的时间表

通过表4能够清楚看到不同规模下，使用神经网络算法、粒子群算法和遗传算法求解纳什均衡的时间。不同算法的求解时间结果对比图，如图3所示。

通过图3可以看出，神经网络算法求解纳什均衡解的时间明显长于遗传算法的求解时间，而粒子群算法在作战规模较小的时候运算时间短于遗传算法，而一旦网络规模增大，它的运算时间会长于遗传算法的求解时间，考虑实际作战规模的影响，应该优先选择遗传算法求解纳什均衡。因此，通过对比，进一步验证了所构建模型的合理性和算法的可行性，为解决合成分队动态武器目标分配问题提供一定支撑。

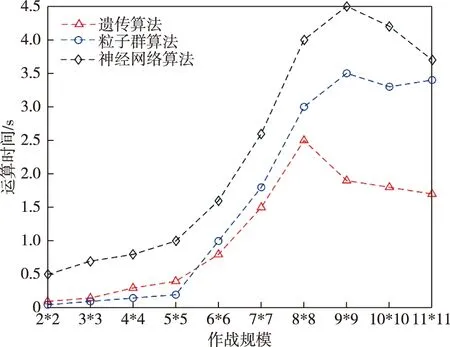
图3 仿真结果图

5 结束语

合成分队敌我双方的攻防过程实际上就是一场动态博弈过程，考虑实际作战存在许多不完全信息，提出了一种基于不完全信息的多武器多目标博弈模型，将动态武器目标分配问题转化为求解纳什均衡的过程，借助遗传算法给出了求解思路，利用仿真证明了本文构建的模型和求解算法的有效性，可以提高指挥决策的科学性。在后续研究中，将进一步考虑武器资源是否正常供应、战场态势等因素，对合成分队的多武器多目标分配问题进行研究，提高均衡解的精确性和适用范围。