颗粒级配对碎屑流运动速度影响的滑槽试验研究

蒋金晶 许强 郑光 彭双麒 王卓 陈达

摘要：滑坡-碎屑流是一种突发性地质灾害，具有速度大、破坏性强等特点。滑坡-碎屑流灾害发生时，不同粒径颗粒组成的碎屑流体运动速度差异较大。为了探究颗粒级配对碎屑流运动速度的影响，设置了单一粒径组、三粒径组以及全粒径组共14种不同级配的工况进行碎屑流滑槽实验，并引入分形维数D对颗粒级配进行量化，获得了最大运动速度与颗粒级配的关系。结果表明：在单一粒径工况下，随着粒径由小到大，碎屑流与底面的摩擦形式由滑动摩擦变为滚动摩擦，颗粒的摩擦耗能减小，碎屑流体运动速度增大;在混合粒径工况下，碎屑流在运动过程中会出现明显的分层现象，而初始级配决定了其中垫层的厚度与结构;伴随着分形维数D和细颗粒含量的减少，运动过程中的垫层厚度也同步减小，导致碎屑流的运动速度增大。

关 键 词：滑坡-碎屑流; 运动速度; 滑槽实验; 颗粒级配; 分形维数

中图法分类号： P642.2

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.05.031

0 引 言

滑坡-碎屑流具有运动速度快、运动距离远、破坏范围广等特点，是一种突发性地质灾害，多发生在中国西部山区。滑坡-碎屑流常给人类的生产生活带来极大的损害，如近年来发生的四川茂县新磨村滑坡[1]、重庆武隆鸡尾山滑坡[2]、贵州关岭大寨滑坡[3]、云南昭通头寨沟滑坡[4]和贵州纳雍普洒村崩塌碎屑流[5-7]等。由于场地条件和滑体岩性的不同，不同的滑坡-碎屑流中岩体在运动过程中的破碎程度不同，导致其堆积体的粒度组成差异较大。头寨沟高速远程滑坡碎屑流中堆积体粒径主要分布于8～64 mm[8];雷波县白沙村滑坡-碎屑流堆积体表层碎屑流颗粒的粒径介于4～6 cm[9];白格滑坡-碎屑流堆积体中碎块石粒径75%以上是0～1 m，有少量块石粒径大于5 m[10]。在滑坡-碎屑流的运动过程中，颗粒之间会不断碰撞[11]从而影响着滑坡-碎屑流的运动速度与致灾范围，因此对不同颗粒级配下滑坡-碎屑流运动速度的研究具有重要的现实意义。

室内物理模拟实验的实验条件可控性高，成为了研究滑坡-碎屑流的主要方法[11-13]之一。赵运会等[14]通过开展室内滑槽模型实验得出滑坡碎屑流的运动距离受控于岩土体类型，且随着碎屑粒径的增大而增大;李天话等[15]研究了不同级配条件下，滑坡碎屑流冲击力的分布特征;郑光等[16]通过室内滑槽实验揭示并解释了滑坡碎屑流堆积体中出现的“反粒序”以及“双峰”现象;王玉峰[17]等通过物理模拟实验对复杂三维地形条件下的滑坡-碎屑流运动与堆积特征进行了研究，首次观察到“X”形共轭堆积脊地貌形态的形成。

Davies[11]通过室内滑槽实验模拟了碎屑流的冲出过程，发现碎屑流的冲出距离受到底摩擦系数和内摩擦系数控制;Phillips[13]等研究了一大一小两种粒径材料组成的碎屑流的冲出情况，发现两种颗粒混合后颗粒流的运动性会增强。Cagnoli[18]研究了不同粒径模型运移距离和颗粒运动特征，发现颗粒越细运移距离越远。 前人通过室内物理模拟实验在滑坡碎屑流的研究中取得了丰硕的成果，但是对于不同颗粒级配下碎屑流运动速度变化的研究较少。本文通过室内滑槽实验，利用高速数字相机对碎屑流的运动过程进行拍照，对不同粒径级配下碎屑流运动速度变化进行了分析研究，并获得了相关规律。

1 碎屑流滑槽实验方案

1.1 实验装置

图1为本次室内物理模拟实验的滑槽装置，斜槽倾角为30°。组件2上雕刻有5 mm间隔的网状刻度用以精确记录碎屑流运动距离。

1.2 实验方案

1.2.1 实验材料

在碎屑流滑槽实验中，一般情况下采用聚氯乙烯颗粒、玻璃珠、工程塑料珠等球形颗粒，或不同矿物成分的砂、砾等棱角形材料。考虑到碎屑流多为岩质，并且实际碎屑流堆积体的颗粒形状多为棱角形，因此本次实验选取与之形态、力学性质最为接近的角砾状石英砂作为相似材料。据统计，鸡尾山滑坡碎屑流堆积体厚度约为30 m[2]，关岭滑坡的堆积厚度约5～20 m[3]。考虑到堆积厚度一般大于滑移区厚度，所以取碎屑流滑移过程中的平均厚度为10 m，

其中堆积体中停积的块石粒径范围为1～10 m。为了能够在室内滑槽中进行模拟，取如下相似关系：

N=h10=d1～10（1）

式中：N为几何缩尺比例系数;h为试验中碎屑流颗粒在滑槽中运动时的厚度;d为试验颗粒直径。

前期测试实验中发现，1 mm的材料释放后在滑槽中运动的厚度约为10 mm，故实验的几何缩尺比为N=1/1 000。则换算的实验粒径范围为1～10 mm。本次实验最终采用1.0，2.5，5.0，7.5 mm 4种粒径（见图2）的石英砂进行实验，颗粒材料物理参数见表1。

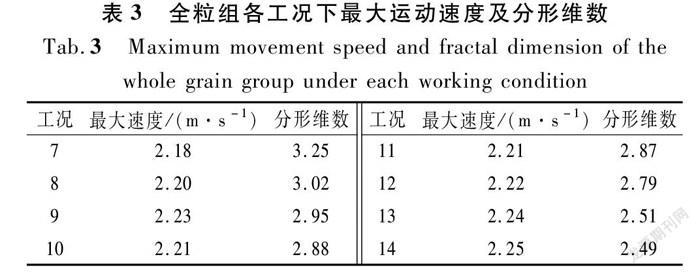
本次实验在保证斜槽倾角、滑源物料体积一致的前提下，通过改变颗粒级配共设计了14种不同工况（见表2）。

1.2.2 实验步骤

每组实验开始前，使闸门与滑槽底板垂直，为了保证颗粒启动时的初始能量相同，每次滑动前都要将滑缘区物质堆积为相同形状（见图3）。在堆积完成以后，迅速打开闸门，使石英砂自然释放，并使用高速数字相机对碎屑流运动过程进行拍摄以便于分析碎屑流的速度变化。在碎屑流停积完成以后，记录各工况下碎屑流的最大运动距离。

2 实验数据分析

2.1 碎屑流前段選定

为了研究不同级配下碎屑流运动速度的变化情况，选取碎屑流前段的平均运动速度进行分析。由于实验中碎屑流体受到滑槽两侧墙体的摩擦作用，流体流动过程中出现中部凸出的现象，形成“凸”字形流动状态，如图4中b点所示，在使用PIVlab进行速度提取时选取凸出部分后5 cm的矩形区域作为分析区，如图4中c点绿色矩形所示。

2.2 不同颗粒级配碎屑流前段运动速度变化

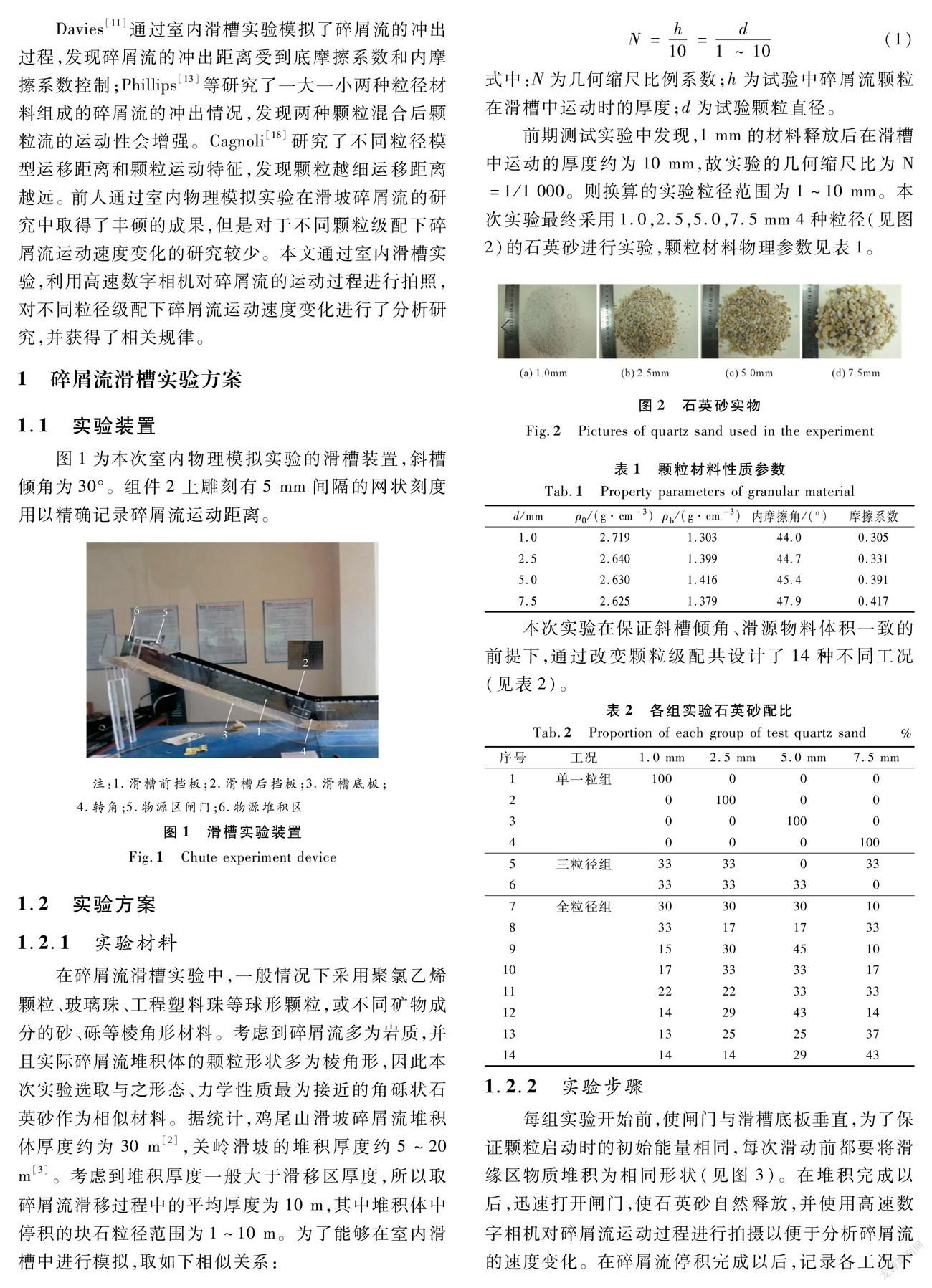
图5表示单一粒组碎屑流在不同位置处的运动速度。由图5可以看出：4种工况条件下，速度呈先增大然后减小的趋势，且均在75 cm位置处达到峰值，其峰值速度分别为2.20，2.23，2.29，2.35 m/s，表明单一粒径条件下，随着颗粒粒径的增大，碎屑流最大运动速度增加。当碎屑流前段位于0～50 cm内时，工况1和2下的碎屑流运动速度大于工况3和4，表明颗粒级配对碎屑流最大运动速度的影响并不是从刚开始滑动时产生的，而是在碎屑流的流动过程中逐渐产生影响。

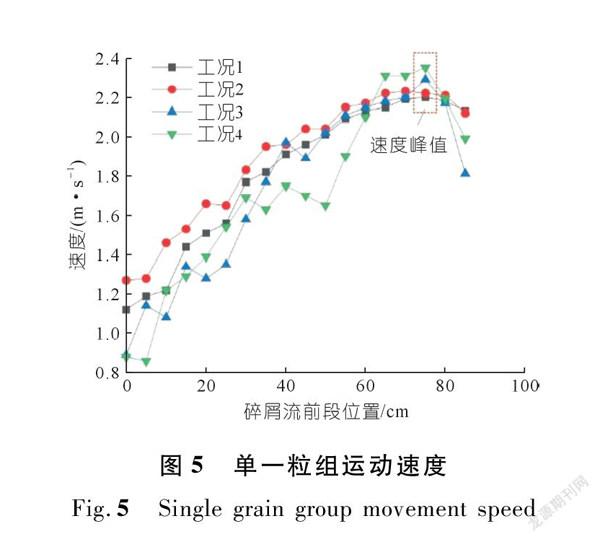
图6表示三粒组碎屑流在不同位置处的运动速度。由图6可以看出：工况5和6下的碎屑流随着滑槽向下运动速度也呈先增大后减小的趋势，且均在70 cm处到达峰值，其峰值速度分别为2.32 m/s和2.28 m/s。在碎屑流运动速度到达峰值之前，工况5和6下碎屑流前段的运动速度比较平稳，曲线波动均较小;且在各个位置处，工况5下碎屑流前段运动速度几乎都大于工况6下碎屑流前段的运动速度。这表明在三粒组工况下，颗粒级配从碎屑流一开始滑动就对其产生了影响，并且整体表现为大颗粒的含量越高，碎屑流运动速度越大。

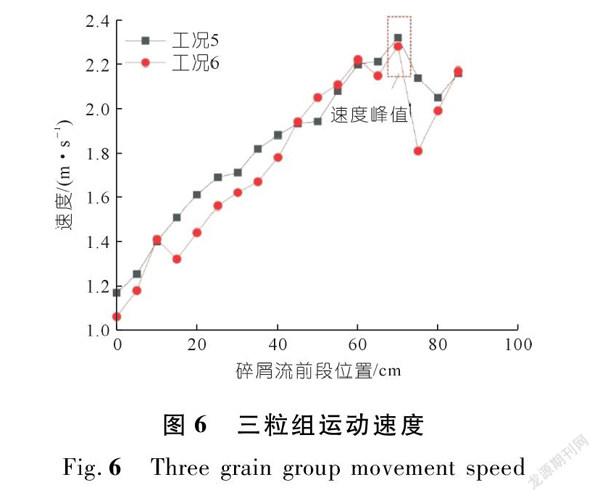
图7表示全粒组碎屑流在不同位置处的运动速度。为了图示信息清晰，将全粒组工况分为工况7～10、工况11～14。由图7可以看出，8种工况条件下的碎屑流随着滑槽向下运动，速度呈先增大然后减小的趋势。工况7～14下碎屑流出现峰值速度的位置依次为75，70，70，75，75，85，70，75 cm;各工况的峰值速度列于表3。在碎屑流运动速度到达峰值之前，各工况下碎屑流前段的运动速度均比较平稳，没有出现较大波动。通过对单一粒组工况以及三粒组工况的碎屑流最大运动速度进行分析得出，大粒径石英砂的占比增加使碎屑流运动速度增大。在全粒组中，大颗粒的占比没有明显优势，所以需要引入一个系数来量化每个工况下的粒径分布。在对滑坡碎屑流的堆积体粒径分布进行研究以后发现其粒径分布具有分形的特征[20]，这种特征是由于在滑坡运动过程中，颗粒不断碰撞发生破裂所导致[21]。分形维数D可以用来量化这种破碎程度，且在粒组分析中具有较大的优势，已被逐渐应用于碎屑流粒径组成的定量描述[22-23]。因此，本文也将采用分形维数D对全粒组工况下的粒径分布进行量化，采用文献[24]中的方法绘制了各工况的粒度与颗粒数关系图（见图8），并对其进行线性拟合，得到直线的斜率即为该工况下的分形维数，如表3所列。

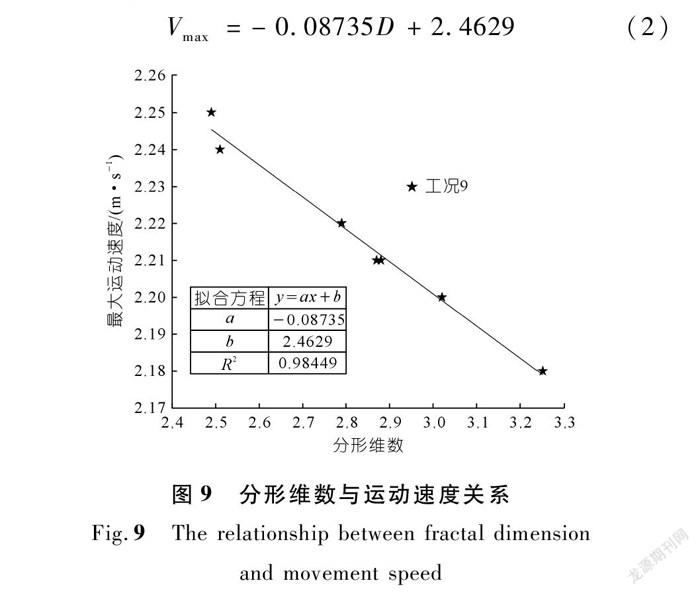
为进一步分析最大运动速度与分形维数的关系，将表3所示的最大运动速度与分形维数进行线性拟合，结果如图9所示。

从图9中可以看出：碎屑流最大运动速度随着分形维数D增大而减小，除去离散性较大的工况9，可对其余工况下分形维数与碎屑流最大运动速度进行线性拟合（R2=0.984 49）。分形维数D与碎屑流最大运动速度Vmax的关系式如下：

Vmax=-0.08735D+2.4629（2）

通过观察原始数据，发现工况9的照片较暗，因此认为光线问题影响了照片质量，导致使用PIVlab进行分析时识别不够准确。为此，在保证光源充足的条件下，对工况9进行了补充实验，分析得出工况9的最大运动速度为2.2 m/s。

将修正过的最大运动速度与分形维数进行再次拟合，如图10所示。由图10可以看出，碎屑流最大运动速度随着分形维数的增大而减小。当分形维数D大于2.5时，碎屑流最大运动速度与分形维数之间具有明显的线性关系，对其进行线性拟合（R2=0.981 36）得到分形维数D与碎屑流最大运动速度Vmax的关系式如下：

Vmax=-0.08875D+2.4657（3）

本次实验记录了各工况下碎屑流运动的最远距离及碎屑流前段达到最大速度时的位置，因此可以利用谢德格尔法[5]反算运动速度，用以与PIV分析结果进行对比，谢德格尔法计算公式如下：

v=2g（h-vl）（4）

μ=HL（5）

式中：g为重力加速度，取9.8 m/s;h为崩塌源区后壁最高点至计算点的竖直高度差，m;l为崩塌源区后壁最高点到计算点的水平距离，m;μ为等效摩擦系数;H为崩塌后缘到前缘的最大高度差，m;L为崩塌后缘到前缘的最大水平距离，m。

图11表示由PIVlab提取的碎屑流最大运动速度与谢德格尔公式计算所得的碎屑流最大运动速度柱状对比。由图11可以看出：谢德格尔法计算速度与PIVlab分析速度呈现出较好的一致性，但是谢德格尔法算所得碎屑流运动速度均大于利用PIVlab分析所得速度。这是由于谢德格尔法是使用等效摩擦系数对碎屑流运动速度进行估算，而等效摩擦系数等于崩塌后缘到前缘的最大高度差与崩塌后缘到前缘的最大水平距离之比，使得摩擦系数较小，导致计算所得运动速度偏大。

3 讨 论

单一粒径工况下，假设碎屑流体在斜槽上运动时，都以滑动为主。在不考虑碰撞耗能，岩体破裂耗能的情况下，按照能量守恒原理[25]，满足下式：

mgH=12mv2+fL（6）

式中：m为石英砂的总质量，g为重力加速度;H为石英砂堆积于滑源区时与地面之间的垂直高差;v为碎屑流运动速度;f为摩擦阻力;L为碎屑流运动距离。

由公式（5）可知：石英砂的重力势能只转换为动能和摩擦耗能，摩擦系数越小则摩擦耗能越小，碎屑流运动速度就越大。由表1可以看出，随着石英砂颗粒粒径增加，摩擦系数增大。依据能量守恒原理，单一粒径工况下，粒径越大则运动速度越小，显然与本实验结果相反（见图5），这说明在运动过程中，不同粒径组成下的碎屑流并不是都以滑动为主。由图12可以看出，在只有1 mm粒徑石英砂的碎屑流体中，流体的表面非常平整，几乎没有跃起的石英砂颗粒;然而在只有7.5 mm粒径石英砂的碎屑流体中，流体的表面有许多跳动的石英砂颗粒。这表明颗粒粒径越小，在运动过程中排列越紧密，越容易发生整体滑动，从而导致与底面的摩擦表现为滑动摩擦;粒径越大，各颗粒之间空隙越大，排列越松散，从而导致与底面的摩擦更多的表现为滚动摩擦（见图13）。

混合粒径工况下，在运动过程中，小颗粒在分选作用下迁移至流体底部，在流体底部形成“垫层”，大颗粒在“垫层”之上（见图14）。初始颗粒级配会影响垫层的厚度，即小颗粒含量减少时，垫层厚度随之减小。垫层颗粒与滑面紧贴，处于受剪切区，垫层越薄，越容易在剪切作用下发生滚动，而滚动摩擦系数小于滑動摩擦系数。所以在发生滚动以后摩擦耗能会降低，从而导致碎屑流运动速度增加。因此，垫层越薄，则碎屑流运动速度越大，这解释了当分形维数减小（小颗粒含量减小），碎屑流运动速度增大的现象。

另外，Cagnoli[18]的研究表明：颗粒越小，碎屑流运动速度越大，这显然与本文得出的结论相反，出现这种差异主要原因是流动状态的不一致：Cagnoli采用的是0.5～1，1～2，2～3 mm粒径的火山岩块。这3种粒径组成的碎屑流体在滑槽中流动较稳定，类似于一个整体“滑块”沿着滑槽向下运动，与底面的摩擦均表现为滑动摩擦。颗粒粒径越大，形成的“滑块”底面越粗糙，摩擦耗能就越大，最终导致碎屑流运动速度随着粒径增大而减小。

4 结 论

本文进行了不同颗粒级配下的滑坡碎屑流滑槽实验，引入分析维数探讨了颗粒级配对碎屑流运动速度的影响，得到主要结论如下：

（1） 单一粒径工况下，颗粒粒径越小，在运动过程中排列越紧密，越容易发生整体滑动，从而导致与底面的摩擦表现为滑动摩擦;粒径越大，各颗粒之间空隙越大，排列越松散，从而导致与底面的摩擦更多的表现为滚动摩擦，使得碎屑流体运动速度随粒径增大而增加。

（2） 混合粒径工况下，分形维数D与碎屑流最大运动速度Vmax之间有明显的线性关系，Vmax随着D增大而减小，其关系式为：Vmax=-0.088 75D+2.465 7。

（3） 混合粒径工况下，小颗粒在分选作用下迁移至流体底部并形成“垫层”。“垫层”颗粒与滑面紧贴，处于受剪切区，垫层越薄，越容易在剪切作用下发生滚动而降低颗粒与滑面之间摩擦耗能，使得碎屑流运动速度增大。

参考文献：

[1] 张涛，杨志华，张勇双，等.四川茂县新磨村高位滑坡铲刮作用分析[J].水文地质工程地质，2019，46（3）：138-145.

[2] 许强，黄润秋，殷跃平，等.2009年6·5重庆武隆鸡尾山崩滑灾害基本特征与成因机理初步研究[J].工程地质学报，2009，17（4）：433-444

[3] 殷跃平，朱继良，杨胜元.贵州关岭大寨高速远程滑坡—碎屑流研究[J].工程地质学报，2010，18（4）：445-454

[4] 唐川.昭通头寨沟特大型灾害性滑坡研究[J].云南地理环境研究，1991（2）：64-71

[5] 郑光，许强，巨袁臻，等.2017年8月28日贵州纳雍县张家湾镇普洒村崩塌特征与成因机理研究[J].工程地质学报，2018，26（1）：223-240.

[6] 彭双麒，许强，李骅锦，等，基于高精度图像识别的堆积体粒径分析.工程地质学报，2019，27（6）：1290-1301.

[7] 彭双麒，许强，郑光等，碎屑流堆积物粒度分布与运动特性的关系：以贵州纳雍普洒村崩塌为例[J].水文地质工程地质，2018，45（4）：129-136.

[8] 王品，徐则民.头寨大型高速远程滑坡碎屑流堆积体的粒度组成[J].山地学报，2013，31（6）：745-752

[9] 曾琇舒，冯文凯，易小宇.雷波县白沙村滑坡-碎屑流粒度分布特征与运动过程关系[J].科学技术与工程，2019，19（6）：38-43

[10] 彭双麒，许强，郑光，等.白格滑坡-碎屑流堆积体颗粒识别与分析[J].水利水电技术，2020，51（2）：144-154

[11] MANZELLA I，LABIOUSE V.Flow experiments with gravel and blocks at small scale to investigate parameters and mechanisms involved in rock avalanches[J].Engineering Geology，2009，109：146-158.

[12] DAVIES T R，MC SAVENEY M J.Runout of dry granular avalanches[J].Canadian Geotechnical Journal，1999，36（2）：313-320.

[13] PHILLIPS J C，HOGG A J，KERSWELL R R，et al.Enhanced mobility of granular mixtures of fine and coarse particles[J].Earth and Planetary Science Letters，2006，246：466-480.

[14] 赵运会，樊晓一，冷晓玉，等.滑坡碎屑流运动特征的模型试验研究[J].人民长江，2016，47（9）：84-90.

[15] 李天话，樊晓一，姜元俊.不同颗粒级配滑坡碎屑流等效冲击力及作用位置分布研究[J].山地学报，2018，36（5）：740-749

[16] 郑光，许强，彭双麒.滑坡-碎屑流的堆积特征及机理分析[J].工程地质学报，2019，27（4）：842-852

[17] 王玉峰，许强，程谦恭，等.复杂三维地形条件下滑坡-碎屑流运动与堆积特征物理模拟实验研究[J].岩石力学与工程学报，2016，35（9）：1776-1791

[18] CAGNOLI B.Effect of grain size in mobility of dry granular flows of angular rock fragments：An experimental determination[J].Journal of Volcanology & Geothermal Research，2010，193（1）：18-24

[19] 郑光，许强，彭双麒，岩质滑坡-碎屑流的运动距离计算公式研究[J].岩土力学，2019，40（12）：4897-4907

[20] CROSTA G B，FRATTINI P，FUIS N.Fragmentation in the Val Pola rock avalanche，Italian Alps[J].Journal of Geophysical Research：Earth Surface，2007，112（F01006）：1-23.

[21] SAMMIS C，KING G，BIEGEL R.The kinematics of gouge deformation[J].Pure and Applied Geophysics，1987，125（5）：777-812

[22] DUNNING S A.Rock avalanche in high mountains[D].London：University of Luton，2004.

[23] DUFRESNE A，DUNNING S A.Process dependence of grain size distributions in rock avalanche deposits[J].Landslides，2017，14：1555-1563.

[24] HOOKE R L，IVERSON N R.Grain-size distribution in deforming subglacial tills：role of grain fracture[J].Geology，1995，23（1）：57-60.

[25] 鄭光.滑坡-碎屑流远程运动距离研究[D].成都：成都理工大学，2018.

（编辑：刘 媛）

Chute experimental study on effect of particle gradation on movement speed of landslide-debris flow

JIANG Jinjing，XU Qiang，ZHENG Guang，PENG Shuangqi，WANG Zhuo，CHEN Da

（State Key Laboratory of Geohazard Prevention and Geoenvironment Protection，Chengdu University of Technology，Chengdu 610059，China）

Abstract：

Landslide-debris flow is a sudden geological disaster，which has the characteristics of high speed and strong destructiveness.When landslide-debris flow occurs，the grain composition has a great influence on the movement speed of landslide-debris flow.In this paper，14 different gradation conditions of single particle size group，three particle size group and whole particle size group were set to explore the effect of grain composition on the movement speed of landslide-debris flow.The fractal dimension D was introduced to quantify the grain composition，and the relationship between the maximum velocity and grain composition was obtained.The results showed that in single particle size condition，when the particle size developed from small to large，the friction form between the particle flow and the bottom surface changed from sliding friction to rolling friction，the friction energy consumption of particles decreased，and the velocity of debris fluid increased.Under the condition of mixed particle size，the landslide-debris flows had obvious stratification during the movement process，and the initial gradation can determine the thickness and structure of the cushion.With the decrease of the fractal dimension D and the fine particle content，the cushion thickness during the motion also decreased synchronously，leading to the increasing velocity of the debris flow.

Key words：

landslide-debris flow;movement speed;chute experience;grain composition;fractal dimension