基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度

徐玉琴 方 楠

（华北电力大学电气与电子工程学院 北京 102206）

0 引言

近年来，为缓解能源短缺与环境污染等问题，可再生能源的大量并网已成为发展趋势，但因可再生能源无法消纳而导致的弃风、弃光问题尚待解决。2021 年全国能源工作会议强调，要加快风电光伏发展，大力提升新能源消纳和储存能力，进一步优化完善电网建设。随着“能源互联网（energy internet）”[1-2]概念的提出，基于多能流耦合互补提高清洁能源消纳与推动能源体系转型升级[1,3]受到业界重视。在多能耦合的各种形式中，天然气良好的经济效益与环境效益使其地位突出。国家统计局发布的生产情况指出，2020 年生产天然气1 888 亿m3，连续四年增产100 亿m3。随着近年来电转气（Power to Gas,P2G）技术的发展，电力系统与天然气系统耦合日益加深。电-气互联系统（Integrated Electricity-Gas System,IEGS）作为多能流耦合互补的新模式，受到专家学者的广泛关注。

IEGS 包含电力网络、天然气网络与使其相互转换的能量转换装置，如燃气轮机、P2G 装置等，能够有效地提高系统的新能源消纳能力，提高系统运行效率。目前，已有许多专家学者对IEGS 的优化调度问题展开研究。文献[4-5]在运行成本的基础上，考虑P2G 设备加入对系统削峰填谷能力的影响，在模型中加入削峰填谷目标；文献[6-7]建立了考虑天然气系统慢动态特性的优化模型。同时，随着环保意识的提高，电力市场的改革，IEGS 的优化调度不能仅局限于经济目标，需要同时考虑污染物排放、系统削峰填谷能力、购电费用等。实际上，IEGS 多目标优化调度模型包含多个目标且具有非凸非线性的特点，复杂程度大，求解困难。启发式优化算法无需考虑模型中的非凸非线性问题，按照一定的搜索规则在满足约束的情况下不断迭代更新，得到Pareto 前沿解集[8]，是解决多目标非线性非凸问题的有效思路，常见算法包括非支配排序多目标遗传算法（Non Dominated Sorting Genetic Algorithm-II,NSGA-II）、多目标差分进化算法（Multi-Objective Differential Evolution,MODE）等。文献[9]提出一种强化多目标差分进化算法求解非凸非线性的电-气互联系统最优潮流问题；文献[10]对相互冲突的多目标决策问题进行模糊处理，结合带精英策略非支配排序遗传算法（Differential Non Dominated Sorting Genetic Algorithm-II,DNSGAⅡ）对问题进行求解；文献[11]提出自适应差分进化算法对配电网多目标无功优化模型进行求解，并用灰色关联决策法从 Pareto 最优解集中得到折中最优方案。但启发式算法应用于大型电网优化调度问题依然耗时过长[8,12]；多目标优化问题的传统思路是将多目标通过加权求和法[4]、ε-约束法、法线平面交叉法（Normal Boundary Intersection,NBI）、基于几何映射的规格化平面约束法（Normalized Normal Constraint,NNC）[13-14]等转换为单目标优化问题，快速求解。文献[11]提出一种求解Pareto前沿的方法，结合NNC 和GAMS/CONOPT 求解器获得了三目标优化问题均匀分布的Pareto 前沿，但是求取完整前沿的耗时较长；文献[15]提出一种增广ε-约束法，避免弱Pareto最优解的产生，并通过避免冗余迭代加速进程；文献[16]采用NBI 法求解三目标优化问题，得到均匀分布的Pareto 前沿，并采用熵权双基点法得到折中最优解。实际上，NBI 法需要将目标函数引入约束条件，容易导致模型的非凸，且无法解决三目标以上的优化问题；ε-约束法的应用受目标函数的影响较大[17]，且生成的Pareto 前沿集不均匀。文献[18]通过多目标加权模糊规划解决多目标优化问题，将多目标转换为求解隶属满意度最大的单目标问题，采用GAMS 软件求解，但是受主观偏好影响大。非凸非线性模型求解复杂，且随着优化模型规模的增大，计算速度缓慢且无法保证获得全局最优解。通过分段线性化[19-21]或凸松弛[22-24]等方式将非凸模型转换为凸优化模型，降低模型求解难度是解决非凸非线性模型求解问题的一般思路。

基于上述研究与存在问题，本文建立了一个考虑风电接入，以燃气轮机、P2G 设备耦合的IEGS 安全约束四目标优化调度模型，通过分段线性化方法处理非线性目标函数，解决将目标函数转换为约束条件导致的模型非凸问题；引入McCormick 方法与二阶锥（Second Order Cone,SOC）松弛处理管道流量方程，将非凸非线性模型转换为混合整数凸优化模型，加入气压差惩罚系数使约束收紧；并提出一种将ε-约束法与NBI 法结合的方法求解四目标优化调度模型，得到一系列均匀分布的Pareto 前沿集，根据熵权双基点法得到综合最优方案。

1 IEGS 联合优化调度

IEGS 由电力网络与天然气网络通过燃气轮机与P2G 设备耦合形成，火电机组、风电机组与燃气轮机向电力网络供应电能，如图1 所示。当系统中电能过多以及风电充足电力网络无法消纳时，可通过P2G 设备转换为天然气输送至天然气网络。

图1 IEGS 基本结构 Fig.1 Basic structure of IEGS

现阶段，我国电力网络与天然气网络属于不同运营商管理，存在信息壁垒与利益冲突。为进一步提高能源利用效率与源网经济性，未来可能的方向是政府从经济性、环境效益等角度出发，打破电网与天然气网络管理方之间的约束边界与壁垒，以大统筹的方式进行统一管理[25]。统一调度机构将两个网络看作整体进行优化，根据电力网络与天然气网络的数据信息构建优化目标，形成调度指令，实现IEGS的整体优化。

2 多目标优化模型

IEGS 优化调度应在保证系统安全稳定运行的同时，合理配置资源，提高设备利用率和系统经济效益。若仅以系统运行成本为优化目标，能有效减少煤耗、弃风量，但节能调度可能导致购电成本上升，增加企业运营压力，也难以保证污染气体排放量的优化[26]。因此，在发电调度中，降低系统运行成本、降低污染气体排放量、降低购电购气费用等多个目标[12]的重要程度应有所不同，随实际运行情况而改变。同时，P2G 的接入使IEGS 具有一定的削峰填谷能力，能够有效平抑净负荷波动，提高系统可靠性[4]。

基于此，本文以IEGS 运行成本、污染气体排放量、削峰填谷指标及购电购气费用作为优化目标，电力网络约束、天然气网络约束与耦合约束作为约束条件，构建IEGS 多目标优化调度模型。

2.1 目标函数

1）IEGS 运行成本

本文构建IEGS 总运行成本F1包括燃煤机组发电的煤耗成本，燃煤机组起停机成本，储气罐储气成本，电转气运行成本以及为减少弃风率引入的弃 风惩罚费用，即

式中，PM,i,t为火电机组i在t时段出力；T0为调度总时段；ΩM为火电机组集合；ΩP2G为电转气设备集合；ΩW为风电机组集合；OCP2G,n为P2G 设备的单位运行费用；LP2G,n,t为t时段第n个P2G 设备消耗的有功功率；OCW,k为单位弃风惩罚费用；ςk,t为t时段第k个风电场的弃风率；PW,k,t为第k个风电场在t时段的可用有功功率；为t时刻第m个储气罐抽气量；为单位抽气费用；f(PM,i,t)为t时段火电机组i的出力-运行成本函数关系，即

式中，Ai、Bi、Ci为机组i的燃料成本系数；IM,i,t为火电机组i在t时段的运行状态，为0-1 变量。g(IM,i,t)为火电机组i的起停机成本，表示为

式中，CSU,i,t为起机成本；CSD,i,t为停机成本。

2）污染气体排放量

火电机组在运行过程中会产生大量的有害气体，过量排放会对周边环境造成严重污染。本文主要考虑硫氧化物排放量，污染气体排放量为[8]

式中，ϑi,1、ϑi,2为污染气体排放量系数，可通过气体排放量与有功出力数据近似拟合得到。

3）削峰填谷指标

以净电力负荷[4]为削峰填谷对象，利用P2G 设备与燃气轮机使电力系统与天然气系统耦合加强。当风电过多时通过P2G 设备转换为天然气储存，当负荷过多时利用燃气轮机快速响应能力将天然气转换为电能，平滑净负荷曲线，达到削峰填谷效果。削峰填谷指标可以用相邻时段净负荷差值最小表示，即

式中，Lp,t为t时段p节点电负荷；ΩL为负荷节点集合；PG,j,t为t时段燃气机组j的出力；ΩG为燃气机组集合。

4）购电购气费用

IEGS 购电购气费用包括从火电机组、燃气机组与风电场所购电费以及从气源购买天然气费用。值得说明的是，在统一调度机制中，P2G 设备消耗电能包含在IEGS 系统购电费用中，燃气轮机消耗天然气包含在系统购气费用中。

式中，ΩO为天然气气源供应点集合；CPM,i、CPG,j及CPW,k分别为火电机组i、燃气机组j与风电场k的单位购电费用；CGO,n为气源点n的单位购气费用；GO,n,t为气源点n在t时的购气量。

2.2 电力系统约束

1）电力系统功率平衡约束

2）火电机组出力约束

式中，PM,i,min为火电机组i的最小出力；PM,i,max为火电机组i的最大出力。

3）火电机组热备用约束

式中，ρ为热备用系数。

4）火电机组起停时间约束

式中，TS为最小关停时间；TO为最小开机时间。

5）火电机组起停成本约束

式中，Hi为火电机组i单次起动成本；Ji为火电机组i单次关停成本。

6）火电机组爬坡约束

式中，Ru,i为机组i的爬坡速率；Rd,i为机组i的滑坡速率；Su,i为起动最大升速率；Sd,i为停机最大降速率，本文取

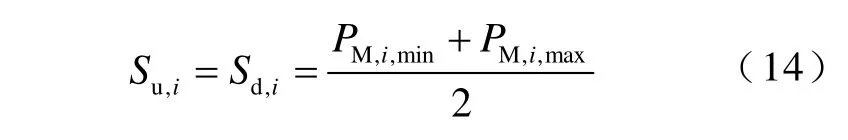
7）潮流安全约束

本文采用直流潮流模型[8]计算线路安全约束，即

式中，Pi,t为节点i在t时刻的有功注入；Dp,t为节点p在t时刻的有功消耗；m、n为线路l两端节点；xmn为支路l电抗值；Pl,mn,max为线路l最大传输功率；Xmi、Xni、Xmp、Xnp为直流潮流模型节点阻抗矩阵中的元素[8]；Gl-i、Gl-p为发电机输出功率转移分布因子，可表示节点i、p的注入功率对线路l的影响。

2.3 天然气网络约束

1）气源流量约束

式中，GO,j,t,max、GO,j,t,min分别为t时刻j供应点天然气源供应天然气流量的上、下限。

2）管道流量约束

本文考虑稳态时的管道流量约束，包括管道流量方程及节点压力约束，即

式中，Gij,t为由节点i向线路ij注入流量；πi,t为节点i在t时刻的压强；dij,+、dij,-为0-1 变量，dij,+为1表示天然气流向为从节点i到j，dij,-为1 表示天然气流量方向为从j到i；κij为管道ij的管道常数。

3）储气罐约束

储气罐能够在天然气流量较多时将天然气临时存储，在天然气供应不足，气负荷需求量过高时提供天然气补给，储气罐约束包括存储总量约束和进出天然气流量约束，可表示为

式中，GS,i,t为t时刻第i个节点储气罐的存储气体量；为t时刻第i个节点储气罐的进气量；为t时刻第i个节点储气罐的出气量。

4）加压站约束

在天然气传输过程中，由于管道摩擦等因素会造成一定程度的压力损耗，因此长距离输送天然气过程中需要配备加压站，通过加压站中的压缩机补偿损耗压力。加压站消耗的能量假设由流过压缩机的天然气提供[4]，则加压站可视为天然气网络的气负荷节点。加压站消耗的能量与流过压缩机的天然气流量有关，加压站约束即压缩机消耗能量与天然气流量关系约束与压缩比约束，可表示为

式中，GLcom,c,t为压缩机消耗能量；γcom,c为能量消耗系数；i、j为压缩机c两端节点；Yc为与第c台压缩机相关的常数。

5）节点流量平衡约束

天然气网络中节点流进量与流出量守恒，节点流量平衡约束为

式中，Ωi为节点i的管道集合；Ωi-c为由节点i供应能量的压缩机集合；GP2G,i,t为节点i的P2G 设备在t时刻注入的天然气；GLd,i,t为节点i的气负荷需求；GLG2P,i,t为节点i的燃气轮机在t时刻消耗的天然气。

2.4 耦合约束

在本文建立的电-气综合能源系统中，电力系统与天然气网络通过燃气轮机和P2G 设备耦合连接，耦合约束包括燃气轮机约束与P2G 设备约束。

1）燃气轮机约束

燃气轮机是电力系统与天然气系统的重要能量转换装置，相较火电机组，具有快速起停、爬坡速率高等优点[27]。燃气机组约束主要包括消耗天然气量与产生电能的等式约束与转换容量限制，即

式中，ξG,i为第i台燃气轮机的转换效率；Hg为天然气热值；PG,i,max为燃气机组i的最大出力。

2）P2G 设备约束

P2G 设备通过电解水与氢制甲烷两阶段反应将富裕电能转换为天然气存储，目前能量转换效率约为65%[28]。P2G 设备约束主要包括消耗电能和生成天然气的等式约束与转换容量限制，设备的最短起停时间约束，如式（22）所示。

式中，ξP2G,i为第i台P2G 设备的转换效率；Ton为P2G 设备的最短起动时间；Toff为P2G 设备的最短停机时间。

3 模型线性化与凸松弛处理

由式（1）～式（22）建立的模型中包含机组状态、天然气流向等0-1 变量，F1中包含二次函数，F3中包含绝对值函数，管道流量方程为二次等式约束，是混合整数非凸非线性模型（Mixed Integer Nonlinear Nonconvex Programming,MINNP），模型复杂，难以直接快速求解[29]。采用线性化技术与SOC 松弛技术处理复杂模型，构建混合整数凸优化（Mixed Integer Convex Programming,MICP）模型，可有效降低求解难度。

1）目标函数线性化处理

系统总运行费用F1中的煤耗成本f(PM,i,t)为二次函数，可通过式（23）分段线性化处理[19]。

式中，m为分段总数；V为机组i在第s分段的最大出力；pi,t,s为火电机组i在t时段第s分段的实际出力；C0,i为机组i运行在最小出力状态时的系统运行费用；Ki,s为机组i在第s分段区间的斜率，通过推导简化可表示为

削峰填谷指标F3为绝对值函数，通过引入辅助变量，增加约束的方式[30]，使其能够线性表示。

2）管道方程SOC 松弛

管道流量方程为非凸非线性方程，导致模型求解困难。通过SOC 松弛技术转换为SOC 约束，使模型易于求解。

考虑到式（17）中包含根号项，无法直接进行SOC 松弛，首先需要等式简化，消除式中的根号项。通过引入辅助变量,χi,t表示节点i气压的二次方值，引入辅助变量,ηij,t表示管道ij两端气压二次方差的大小，则可将式（17）简化为式（26）、式（27）。

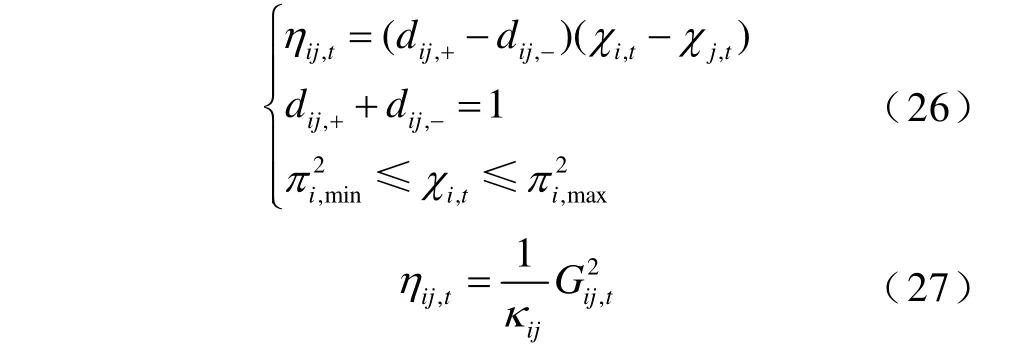
式（26）等式约束中包含两个二进制变量，难以直接求解。结合McCormick 方法与绝对值线性化方法[31]，将式（26）转换为多个不等式约束，如式（28）所示；并将式（27）进行SOC 松弛，如式（29）所示，将非凸非线性模型转换为凸优化模型。

考虑到SOC 松弛使约束过于宽松，两端节点气压差可能在约束范围内被增大，为使约束能够尽量收紧，减少误差，在目标函数中加入节点气压差惩罚项[32]，增强模型紧凑性。

式中，Fk与分别为添加惩罚项前、后第k个目标函数；ωij,k为第k个目标函数的惩罚系数；Ωb为管通集合。

4 模型求解

通过以上处理，得到包含四个优化目标的MICP模型。ε-约束法将次要目标转换为约束条件处理，不受目标函数个数限制，但是求取Pareto 前沿集不均匀且受目标函数影响大；而NBI 法能够求取均匀Pareto 前沿集，但仅适用于三目标优化模型。因此本文提出一种基于增强ε-约束法[20]与NBI 法结合的求解方法，旨在得到系列均匀分布的Pareto 前沿集，最后由熵权双基点法[14]从Pareto 前沿集中选择最优方案。

1）基于增强ε-约束法的目标降维

不失一般性，将多目标优化模型表示为

式中，G(x)为模型中所有等式约束的集合，G(x)=0；H(x)为模型中所有不等式约束的集合，H(x)min≤H(x)≤H(x)max。采用增强ε-约束法对目标函数进行降维处理。首先通过对目标函数进行优先级排序，选择优先级较低的n-3 个目标函数作为约束条件，并增加辅助变量，使目标函数在网格点中能够找到可行的目标函数解，在减少目标个数的同时保证了生成Pareto 前沿集的有效性。

Spearman 秩相关系数[8]对原始变量的分布不做要求，不需要变量间呈现连续、正态分布、线性关系，计算结果会给出变量间的相关系数，适用于电力系统多目标优化问题的相关性排序。

当两个变量间的Spearman 相关系数越接近1时，则两个变量之间的变化趋势越一致；当Spearman 相关系数接近-1 时，表示两个变量之间的变化趋势相反。通过比较n个目标函数Spearman 相关系数的负数个数及大小进行优先级排序，负数个数越多则该目标函数变化趋势与其他目标函数矛盾最大，优先级顺序越低。负数个数相同时，负数越接近-1 矛盾程度越大，优先级顺序越低。

按照优先级顺序从低到高选择n-3 个次要目标函数，通过n组目标函数解的数值确定次要目标函数的最大值和最小值，得到次要目标函数的取值范围为

根据增强ε-约束法，式（31）可写为

式中，l0为常数；lΔi表示目标函数i的重要程度，一般取10-(i-2)；为目标函数Fi引入的辅助变量[8]，使得在相邻网格间能够找到可行解；为将目标函数Fi进行ki等分，得到ki+1 个网格点后，第j个网格点的值，即

通过逐次改变ji值，可以得到(k4+1)(k5+1)…(kn+1)组三目标优化模型，模型的精确度随三目标优化模型的组合数增加而提高。

2）基于NBI 法的三目标优化求解

NBI 法能够有效求解三个目标的优化问题，通过对三个目标分别进行单目标优化，规格化处理，由规格化目标向量生成乌托邦面，乌托邦面上的每一点都可以由三个规格化目标向量线性表示。乌托邦面的准法线向量也可以由解向量表示，通过引入距离变量，改变线性组合系数值，将优化目标转换为最大化距离向量，得到一系列均匀分布的Pareto前沿集，详细原理见文献[14]。最后，根据熵权双基点法得到最优方案，供调度人员参考。本文四目标优化调度模型的完整求解流程如图2 所示。

图2 模型求解流程 Fig.2 Model solving process

5 算例分析

以图3 所示的IEGS 为测试算例。该系统由修改的IEEE 30 节点电力网络和比利时20 节点天然气网络通过P2G 设备与燃气轮机（Gas Fired Units,GFU）耦合而成。其中，IEEE 30 电力网络包含41条线路，6 台燃煤机组，总装机容量4.774 9GW，将电负荷与线路传输功率限制适当降低为标准模型的70%[4]。在电力网络8 节点、26 节点与29 节点处建立风电场，将单位弃风惩罚费用OCW,k统一设置为1 000$/(MW·h)[3]。结合工程实际，为提高风电消纳能力，将电转气设备接入电力网络8 节点、26 节点与29 节点，并与天然气网络20 节点、10节点与13 节点相连，在风电过多时通过P2G 设备消耗电能转换为天然气，输入天然气网络。在电力网络10 节点、15 节点、24 节点处接入燃气轮机，分别与天然气网络2 节点、17 节点与10 节点相连。燃煤机组、P2G 设备与燃气轮机相关参数见附表1～附表3。

附表1 燃煤机组部分相关参数 App.Tab.1 Some relevant parameters of coal-fired units

附表2 燃气机组部分相关参数 App.Tab.2 Some relevant parameters of gas-fired unit

附表3 P2G 设备部分相关参数 App.Tab.3 Some relevant parameters of P2G

图3 电-气互联系统结构 Fig.3 Structure of integrated electricity-gas system

电力系统总负荷、天然气系统总负荷与风电场预测出力结果如图4 所示。

图4 电负荷、气负荷及风电预测曲线 Fig.4 Power load,gas load and wind power forecast curve

5.1 模型精确度分析

本文通过线性化方法简化目标函数，SOC 松弛与气压差惩罚项处理管道流量方程。使用分段线性化方法时，当分段数取4 即可满足精度要求[19]，因此只需进行二阶锥松弛准确性分析即可。引入管道流量方程松弛误差指标δ[32]，进行二阶锥松弛精度测试。

为验证SOC 松弛与气压差惩罚项必要性，通过逐一单目标优化，选择对比第2 时段添加惩罚项前后二阶锥松弛精度，如图5 和图6 所示。

图5 松弛误差（不加惩罚项）Fig.5 Relaxation error (without penalty)

图6 松弛误差（加入惩罚项）Fig.6 Relaxation error (with penalty)

由图5 和图6 对比可得，未加惩罚项时SOC松弛在部分管道过度松弛，导致精度较低，无法保证约束准确有效；在加入惩罚项后，SOC 松弛收紧，精度误差均在10-3数量级，能保证约束的有效性。

5.2 模型优化结果分析

首先进行四个单目标优化模型求解，得到每个单目标优化对应的目标函数向量，利用四个目标函数向量组成的目标函数矩阵生成Spearman 秩相关系数矩阵，得到对应相关系数的值见表1。

表1 Spearman 相关系数 Tab.1 Spearman correlation coefficient

由表1 可得，在Spearman 秩相关系数矩阵中，F3与其他三个优化目标的相关系数均为负值，优先级最低，因此将F3作为次目标函数，通过式（33）及式（34）加入约束条件中。本文取ki=3，即将目标函数F3三等分，得到四组三目标优化模型。通过NBI 法获得四组对应均匀分布的Pareto 前沿，如图 7 所示。假定调度人员主观偏好值为[0.3,0.3,0.1,0.3]，通过熵权双基点法，考虑Pareto 前沿不同解差异的熵权值与调度人员的主观偏好获得最优方案，如图7 中三角形所示。

图7 Pareto 前沿图 Fig.7 Pareto frontier

将最优方案的各目标函数与单目标优化后的目标函数进行对比，结果见表2。对比可得，若仅以运行费用或污染气体排放为单目标优化时，仅考虑如何极大程度地降低火电机组出力并优化各机组出力分配情况，导致净负荷差值增大，同时提高市场购电购气费用；若仅考虑净负荷差值，则可使火电机组出力稳定，维持不变，但极大程度地提高了火电出力与污染气体排放量，且购电购气费用也显著增加；仅考虑购电购气费用时电价较低的机组优先出力，而电价较高的风电与燃气机组则维持在较低水平，增大了弃风量，大大提高了运行费用与污染气体排放量。折中最优解在保证运行费用与购电购气费用维持在较低水平的同时，减少了污染气体排放量与净负荷波动程度。为减少净负荷波动与污染气体排放量，最大限度地消纳风电减少弃风量，灵活调度P2G 设备与燃气轮机出力，减少火电机组出力。

表2 单目标优化解与最优解 Tab.2 Single objective optimization solution and optimal solution

5.3 多场景优化分析

为表明P2G 设备对系统风电消纳、削峰填谷能力、运行费用的影响以及本文算法的优越性，本文设置以下四个场景进行对比分析。

场景1：不考虑P2G 设备的四目标优化-采用本文多目标优化算法；场景2：考虑P2G 设备的四目标优化-采用本文多目标优化算法；场景3：考虑P2G设备的四目标优化-采用加权求和法；场景4：考虑P2G 设备的四目标优化-采用增强ε-约束法。

设置场景3 加权求和法中各目标函数的权重与场景1 中调度人员主观偏好值相同，场景1 与场景2 除P2G 设备外其他条件相同，场景4 以运行费用为主目标函数，采用增强ε-约束法得到Pareto 前沿后通过熵权双基点法得到最优方案。四个场景下折中最优解见表3，各场景下火电机组出力、燃气轮机出力、弃风量与P2G 设备的出力情况如图8 所示。

图8 多场景出力曲线 Fig.8 Multi scenario output curve

表3 多场景最优解 Tab.3 Multi scenario optimal solution

由最优解及出力情况对比分析可得，场景1 不考虑P2G 设备，风电消纳能力受到线路传输容量的约束，弃风量大大增加，本文将弃风惩罚费用加入到系统运行成本中，因此不考虑P2G 设备时运行费用也大大增加；场景3 采用加权求和法求解模型得到的最优解能够有效减少弃风量，但受主观权重的 影响较大，为减少购电购气费用，火电机组的使用大大提高，导致运行费用和污染气体费用增加，燃气轮机的利用率大大降低；场景4 采用增强ε-约束法得到的最优方案的运行成本和污染气体排放量得到显著降低，火电机组出力得到显著抑制，燃气机组出力有所提高，但弃风量相较场景2 有所提高，购电购气费用显著上升，净负荷波动程度也大大高于场景2，证明本文所提算法得到的优化方案具有更好的综合优化效果。

6 结论

本文建立了一个IEGS 四目标优化模型，通过目标函数线性化处理，管道流量方程二阶锥松弛并加入气压差惩罚项的处理使模型非凸非线性转换为混合整数凸优化模型。提出一种结合ε-约束法与NBI法的模型求解方法，通过算例分析，得到以下结论：

1）在管道流量方程二阶锥松弛的同时，将目标函数中加入气压差惩罚项，能大大降低松弛误差，可通过cplex 等商用求解器高效求解。

2）结合ε-约束法与NBI 法的模型求解方法能生成一系列均匀分布的Pareto 前沿，采用熵权双基点法确定的折中最优解综合考虑了调度人员主观意愿与不同解各自熵权值，能够为调度人员的决策提供依据。

3）通过本文建立模型与求解算法得出的最优方案能够实现P2G 与GFU 的灵活调度，大大降低了系统弃风量，提高了系统削峰填谷能力，并降低了污染气体排放量。

P2G 与GFU 的灵活调度对促进IEGS 低碳运行的能力值得进一步深入研究。