550kV GIS 盆式绝缘子小型化设计（二） ——介电分布优化

李文栋 王 超 陈泰然 李文强 宫瑞磊 张冠军

（1.西安交通大学电力设备电气绝缘国家重点实验室 西安 710049 2.国网山东省电力公司泰安供电公司 泰安 271000 3.山东泰开高压开关有限公司 泰安 271000）

0 引言

随着超/特高压输电技术的快速发展和不断成熟，小型化、低制造/运行成本已经成为输电设备的重要发展方向[1-2]。SF6气体绝缘金属封闭开关设备（Gas Insulated Switchgear,GIS）是变电站中的关键电力设备，其小型化精细设计方法具有重要的研究与应用价值。作为GIS 中的关键绝缘部件，盆式绝缘子起到了支撑金属导杆、隔离电位、气室密封隔气等作用[3]。而当其结构设计不合理导致局部电场集中，或制备安装有瑕疵而使得表面出现孔隙缺陷、金属微粒时，SF6气体在均匀及稍不均匀电场中优异的绝缘性能会因局部电场的畸变而迅速劣化，诱发放电击穿，导致盆式绝缘子乃至GIS 设备的绝缘失效[4-5]。

为抑制盆式绝缘子的放电破坏、提升GIS 设备的可靠性、促进其小型化发展，国内外研究者开展了大量的盆式绝缘子及其配套电极结构的优化设计工，如在高压侧中心导体加装金属屏蔽罩[6]、合理改进绝缘子中心嵌件结构[7]、调整盆式绝缘子外法兰附近电极/绝缘结构[8]等。550kV 盆式绝缘子结构如图1 所示。上述方法一方面使得结构复杂度上升，不仅使得盆式绝缘子制造成本提高、安装与运维难度增加，也不利于GIS 设备的小型化发展。另一方面，额外增加的电极结构也会带来附生问题。例如，现有GIS 设备中，为抑制盆式绝缘子外法兰附近的电场畸变，常在接地法兰处设置“R”形屏蔽罩（简称“R”弧结构），或在此处盆体内部嵌入金属屏蔽环[8]，如图1a 所示。对于“R”弧结构，为保证加工精度，往往需焊接后进行人工切削/打磨，不仅费时费力，且容易在加工过程中形成金属尖端，引发局部放电乃至击穿破坏。对于金属屏蔽环，虽然可在一定程度上均化法兰处电场，但易于引发绝缘子开裂，导致盆体的力学性能发生劣化。

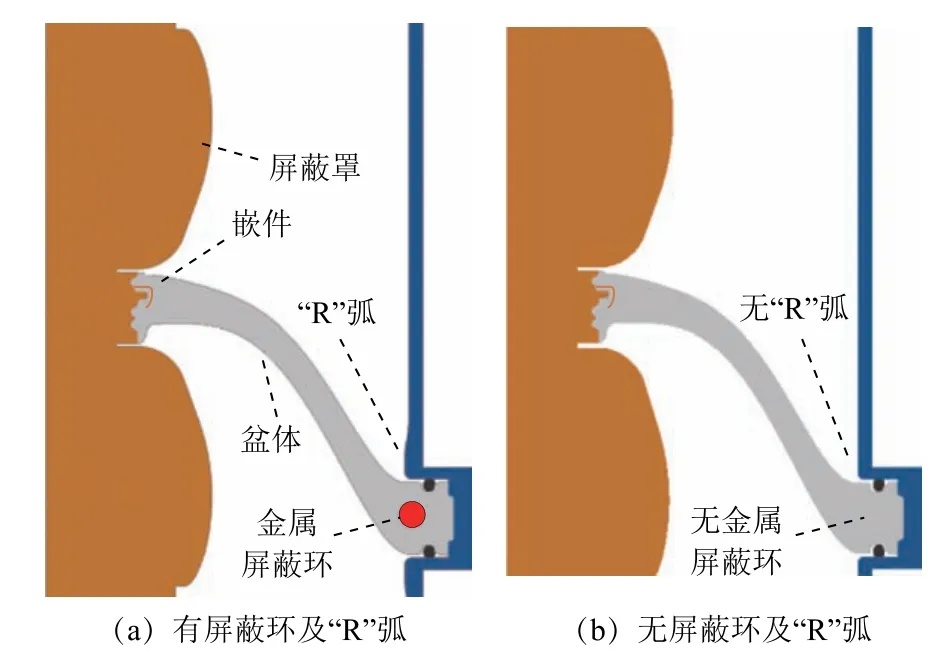
图1 550kV 盆式绝缘子结构 Fig.1 Geometrical structure of 550kV basin-type spacer with or without shield ring and“R”shape shield

近年来，通过材料介电分布优化主动调控电场分布，构建介电功能梯度材料以实现绝缘性能的大幅提升，逐渐成为绝缘结构设计制造领域的研究热点。前期研究表明，通过叠层优化[9-11]、拓扑优化[12-14]等优化设计手段，可构建能够大幅降低绝缘系统最大电场、提升电场分布均匀性的材料介电梯度结构，进而达到均化电场分布、提升耐电强度的目的。这一基于材料特性调整改善电场分布的方法，突破了以往形状优化设计的局限性，为解决高电压等级GIS 小型化提供了新思路、新手段。

在此背景下，针对某型号550kV 交流GIS 盆式绝缘子开展了小型化设计，内容可分为几何形状优化、介电分布优化以及结构制造验证三部分，最终在满足电气强度的基础上，实现罐体绝缘距离缩小15%的设计目标，并达到了绝缘气体使用量减少20%，绝缘/金属材料用量减少10%的有益效果，为低成本、高可靠性以及小型化GIS 设备制造提供了参考。本文在《550kV GIS 盆式绝缘子小型化设计（一）——几何形状优化》（以下简称论文1）的基础上，开展了盆式绝缘子外法兰附近材料介电常数梯度的拓扑优化设计，分析了优化算法参数对电场调控效果的影响，削弱了外法兰附近盆体沿面区域的电应力集中的现象。进一步地，将3D 打印技术与现有的浇注方法相结合，给出了上述介电梯度绝缘结构的制造方法，为后续研究中的样品制备与实验工作提供技术支撑。

1 形状优化的15%小型化盆式绝缘子

文献[15]提出了550kV 盆式绝缘子几何形状优化方法。利用伯恩斯坦多项式描绘盆式绝缘子凸面和凹面轮廓，并以电场分布均化和机械强度维持为目标，基于遗传算法进行多项式各项系数的优化。优化得到的盆式绝缘子为反S 形结构，在绝缘距离缩减10%，且去除外法兰“R”弧结构（图1b）的情况下，凹面沿面最大电场强度仍可减小25%以上。然而，优化后盆体凸面外法兰处金属外壳-绝缘子-SF6气体三结合点区域的最大电场强度从14.52kV/mm 提升到18.13kV/mm，相比于现有绝缘子反而提升了25%，不利于沿面耐电性能的提升。

本文首先采用文献[15]的方法，在绝缘距离缩减15%，且去除外法兰“R”弧结构的情况下进行几何形状的优化。对于优化过程中的有限元电场计算过程，需要注意以下几点：

（1）由于盆式绝缘子直径一般不超过1m，远小于工频交流、操作冲击和雷电冲击时的电磁波波长（300m 以上），故可采用准静态近似，以静电场模型进行电场分布的计算。

（2）计算过程中采用Dirichlet 边界条件，对中心导体与屏蔽罩等高压电极部件施加 1 675kV 电压，外壳罐体予以接地（0V）。

（3）对中心导体、SF6气体界面，外壳罐体以及盆式绝缘子之间界面处的网格进行加密，网格尺寸设为1mm 以提升计算精度。

几何形状优化后的15%小型化盆式绝缘子电场分布如图2 所示。可以看出，绝缘子外部最大电场强度出现在凹面侧的屏蔽罩表面，为23.91kV/mm，内部最大电场强度仍然出现在内屏蔽罩表面，为17.21kV/mm。值得注意的是，凸面法兰处的局部放大图表明，密封圈/绝缘子/气隙三点结合点区域中的气隙电场强度以及法兰转角处的表面场强较高，易于发生局部放电和沿面闪络，导致盆体和密封圈的破坏。

图2 小型化后550kV 盆式绝缘子电场分布云图 Fig.2 Electric field distribution of 550kV basin-type spacer after compact design

图3 定量描述了几何形状优化后15%小型化盆式绝缘子的沿面电场分布。可以看出，除了凸面法兰侧径向坐标250mm 附近的外法兰区域外，盆体沿面电场均低于12kV/mm 的许用值[16]。对于法兰处的电场畸变，仍需采用合理的抑制手段，然而经过反复尝试，作者发现通过几何结构调整难以削弱这一电场集中现象。为此，本文拟引入介电梯度理念，通过在外法兰附近构建介电梯度，使沿面电场呈现两边低、中间高的倒“U”形分布。

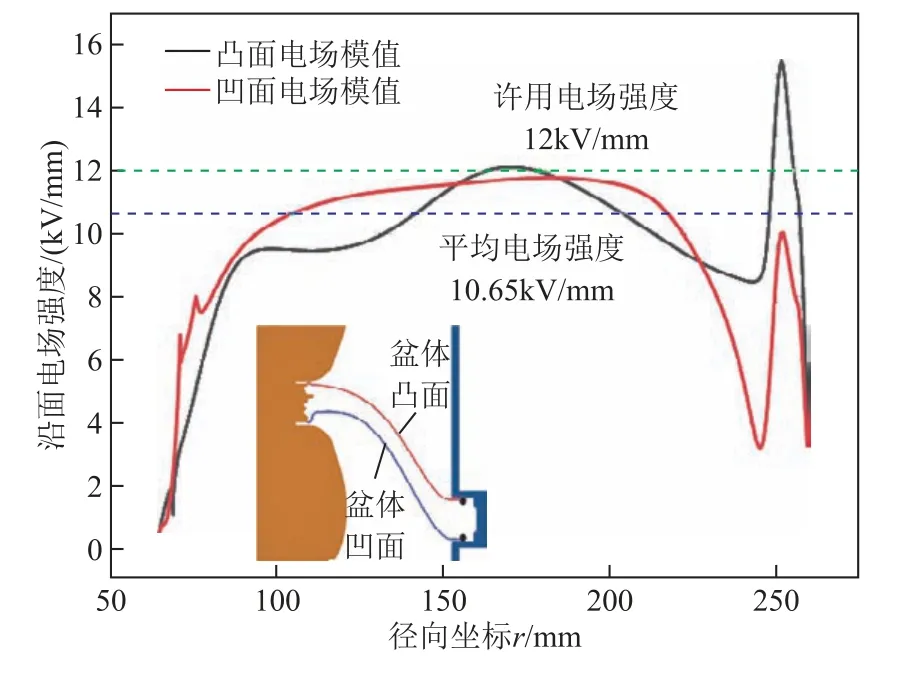
图3 小型化后550kV 盆式绝缘子沿面电场分布 Fig.3 Surface electric field profiles of 550kV basin-type spacer after compact design

2 介电梯度优化设计方法及应用效果

2.1 介电梯度理念简介

介电梯度指的是通过调整绝缘内部的介电常数或电导率的数值以及空间位置，主动改善电场分布，降低耐电强度薄弱区域内的电场[17]。由高斯定理、

电流连续性定理及材料介电常数/电导率本构方程可知：对于给定的绝缘结构，当外施电压频率为f时，电位V与介电常数ε=εrε0（εr和ε0分别代表相对介电常数和真空介电常数）和体积电导率σ之间满足Laplace 方程，即

式中，ω为角频率，ω=2πf；j 为虚数单位。对于电场E，可通过计算电位V的负梯度值予以求取。

根据介电常数与电导率之间的相互关系，式（1）可以简化为以下三种类型：

（1）ωε≫σ时，认为电导率σ的影响可忽略，式（1）转化为静电场下的Laplace 方程，即

（2）ωε≪σ时，认为介电常数ε的影响可以忽略，式（1）转化为恒定电场下的Laplace 方程，即

（3）ωε与σ相互接近时，认为介电常数ε和电导率σ的影响均不能忽略，此时的电场分布介于静电场与恒定电场之间。

本文主要针对高压交流气体绝缘开关设备中的盆式绝缘子开展研究，其在运行过程中承受50Hz 工频交流、雷电冲击以及操作冲击电压，两类冲击电压标准波形（标准雷电波 1.2/50μs 和标准操作波250/2 500μs）的频谱范围分别为100Hz～10kHz 和10kHz～1MHz。图4 给出了不同频率下绝缘材料相对介电常数变化时的ωε取值，并标注了典型介电梯度材料（填充TiO2等高介电常数、低电导率无机填料的聚合物复合材料）电导率的变化范围，即10-15S/m（盆式绝缘子环氧树脂典型值[18]）～10-12S/m（高介电常数TiO2/环氧树脂复合材料典型值[19]）。可以看出，在工频交流、操作冲击及雷电冲击下，材料ωε均比电导率σ高出3 个数量级以上，可忽略电导率的影响。因此，本文采用介电常数梯度材料，调控盆式绝缘子内部及沿面电场分布，抑制凸面外法兰附近的电场集中现象。

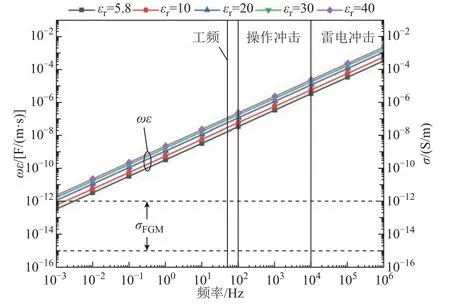
图4 不同频率下介电梯度材料ωε 与σ 关系 Fig.4 Relationship bewteen ωε and σ of dielectrically graded materials under different frequencies

2.2 介电梯度优化设计方法

基于上述讨论，在作者前期研究的基础上[14]，提出了改善盆式绝缘子根部电场的拓扑优化方法。优化问题的数学描述为

式中，设计变量为图5 所示的计算域Ω1内的介电常数分布，r和z分别为二维轴对称模型下的横坐标和纵坐标；m为密度函数因子。为降低图5 中Ω2内的电场模值（即合成电场强度），优化目标的第一分量f1为此区域内的电场积分项，简称电场积分项，Cref为归一化参数。第二分量f2为梯度惩罚项，防止出现“棋盘格”等数值不稳定现象[20]。A、hmesh和ρ分别为计算域Ω1的面积、有限元网格剖分的最大尺寸、以及网格内材料的虚拟密度（取值范围为0～1）。梯度惩罚权值q用于调整f1和f2在总优化目标中的权重。

图5 介电常数梯度绝缘子建模及网格剖分 Fig.5 Modeling and FEM Meshing of permittivity graded insulator

值得注意的是，根据初步的优化结果，即使选取整个绝缘子作为设计区域，介电常数变化位置只出现在Ω1内。因此，为了提高计算效率，在之后的优化过程中，将介电常数的调整区域限定在Ω1内。为了调整Ω1内的介电常数，通过第一项约束条件所示的插值函数，建立虚拟密度与相应网格内介电常数之间的数学关系，其中，εri、εmax和εmin分别为第i个网格内的介电常数、介电常数变化的上限以及介电常数下限。密度函数因子m决定了插值函数的形态，通常其较为合理的取值范围为1～10[12]。

为了减小材料特性发生变化的区域，降低制造难度，如式（4）中约束条件的第3 项所示，将高介电区域的面积限制在设计域面积的0.6 倍以下，并将不等式的中间项除以0.6 后定义为密度利用率，其取值范围为0～1，取值越高说明高介电常数区域在Ω1内所占的面积越大。

在COMSOL 软件中完成上述模型的建立，并采用全局收敛移动渐近线方法（Globally Convergent Version of Method of Moving Asyptotes,GCMMA）进行问题求解。优化容差为10-10，最大迭代次数为20 次，初始网格剖分设为极细化，优化前再对Ω1域内的网格进一步剖分，网格最大尺寸hmesh=4mm。

在计算过程中，当程序优化容差范围小于10-10、高介电区域面积超过约束范围或迭代次数超过20次时计算终止，以最终得到的介电常数分布作为最优计算结果。提取最优计算结果下的介电常数分布以及沿面电场分布，以进行优化效果的分析。

2.3 模型参数的影响及优化效果说明

2.3.1 算法参数m、q对于优化效果的影响规律

不同算法参数下法兰处绝缘介电常数空间分布及电场分布如图6 所示，当相对介电常数上限为20时，优化后在绝缘子根部的中间位置出现了一块近似菱形的高介电区域。密度函数因子m决定了优化得到的高介电区域的边界清晰度和大小。当梯度惩罚权值q相同时，更高的m值下获得的高介电区几何边界更加清晰，同时区域更小。当m值不变时，q值越大，高介电区域的面积越小。就优化效果而言，当m=1，q=0.005 时，法兰转角处的最大电场强度降低程度最大，可由 18.1kV/mm 降低至11.4kV/mm。而当m和q值都较大时（m=3，q=0.01），最大电场强度仅下降1kV/mm。

图6 不同算法参数下法兰处绝缘介电常数空间分布及电场分布 Fig.6 Spatial distribution of permittivity and electric field near the flange under different algorithm factors

图7 所示的不同权重系数下算法的收敛速度是导致优化效果出现差异的原因。根据图7a 可知，保持q值不变，增大m值会导致电场积分项f1的收敛 速度显著减小。同时，图7b 中所示的密度利用率也逐渐降低，这导致程序终止时高介电区域的面积减小，电场优化效果较差。保持m值不变，增大q值具有类似的结论，高q值下收敛速度放缓，达到迭代次数时的优化效果尚未达到最佳。当m=1，q=0.005 时，算法在第7 次迭代计算后即达到较优的电场调控效果。

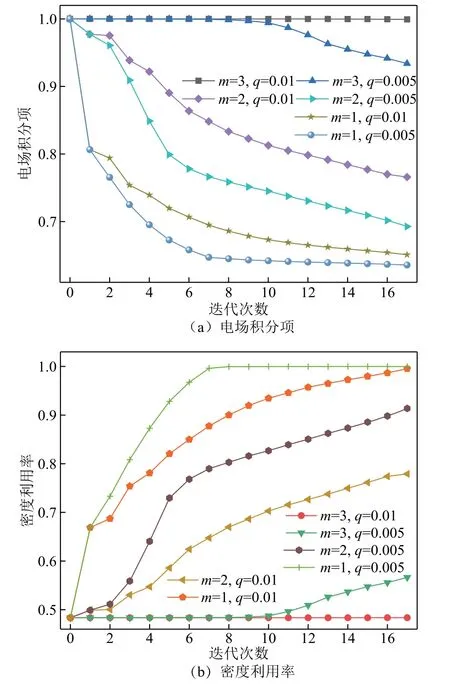
图7 不同算法参数下拓扑优化算法收敛速度 Fig.7 Convergence rate of topology optimization algorithm when selecting different algorithm factors

2.3.2 介电常数上限εmax对优化效果的影响规律

当m和q值分别为1 和0.005 时，优化效果较好，因此本节中m和q值保持不变。相对介电常数上限εmax与法兰转角处的最大电场强度的关系见表1，随着εmax的增大，法兰转角处最大电场强度逐渐降低，当εmax=40时，可降至7.6kV/mm，降幅达55.6%。就介电常数分布而言，当εmax=10 时，高介电常数区域所占面积较小。增大介电常数上限后，高介电常数区域逐渐变大，然而这一区域的形貌变化不明显，均为靠近凸面三结合点处的类菱形结构。

表1 介电常数变化范围对优化效果及材料分布的影响 Tab.1 Influence of permittivity variation range on the optimization effect and material distribution

图8 所示为εmax对算法收敛速度的影响。由图8 可揭示介电常数分布存在差异的原因：增大介电常数上限有利于提高电场积分项的收敛速度（图8a）。避免优化起始阶段图8b 所示的密度利用率过高而造成的局部最优问题。当然，相对介电常数上限过高（如大于30）时，介电梯度材料的制备存在较大困难，高介电常数材料的获取需要向聚合物基体中填充大量的高介电陶瓷填料，不仅使材料易脆断，也不利于加工制备。因此，在介电梯度绝缘件的制备过程中，应适当提升介电常数的上限，满足电场优化、机械强度与加工可行性的需求，这里选取εmax=20 为相对介电常数上限的最优值。

图8 介电常数上限对拓扑优化算法收敛速度的影响 Fig.8 Influence of permittivity’s upper limit on the convergence rate of topology optimization algorithm

2.3.3 小型化介电梯度绝缘子电场优化效果分析

优化后15%小型化介电梯度盆式绝缘子的沿面电场分布及其与对应尺寸匀质绝缘子的对比如图9所示，优化过程中m=1、q=0.005、εmax=20。可以看出，介电梯度的引入对盆体内部区域（r＜150mm）沿面电场分布的影响不大，对外法兰附近（r≥150mm）的电场分布则产生了显著影响。具体地，匀质绝缘件凸面外法兰附近的电场畸变得到了抑制，外法兰附近电场强度从 22.27kV/mm 降低至14.45kV/mm，降低了35%以上，从沿面电场分布来看，尺寸优化+介电梯度优化后，凸面和凹面电场均呈现两端低、中间高的倒“U”形分布，有效抑制了金属-绝缘-气体三结合点的电场畸变现象。

图9 介电常数梯度对沿面电场分布的影响 Fig.9 Influence of permittivity gradient on the surface electric field distribution

表2 给出了绝缘距离缩小带来的绝缘子综合性能指标变化，可以看出，即使绝缘距离缩小15%，盆体凸面和凹面最大电场强度仍能分别降低17.08%和20.90%，同时外壳内径、绝缘材料用量、外壳金属用量以及SF6气体用量分别减少了10.04%、11.87%、9.85%和21.43%。这说明小型化设计起到了减少SF6用量，缩小设备体积，降低原材料消耗的目的。

表2 小型化前后盆式绝缘子与GIS 罐体特性对比 Tab.2 Comparison of basin insulator and GIS vessel before and after compact design

3 小型化介电梯度盆式绝缘子制造方案

根据2.2 节，为了实现法兰处电场的有效抑制，外法兰附近绝缘子内部需嵌入一块近似菱形的高介电区域。而在高介电区域内部，尽管存在一定的梯度变化，但相对介电常数为εmax的区域占据了90%以上的面积。故可将外法兰附近的梯度绝缘改为匀质的介电常数为εmax的区域[14]。根据表1 中m=1，q=0.005，εmax=40 时高介电常数的几何形状，设计了如图10 所示的小型化介电梯度盆式绝缘子。

图10 小型化介电梯度盆式绝缘子的局部和整体结构 Fig.10 Local and overall structures of downsized dielectrically graded basin-type insulator

由图10 可知，小型化的盆式绝缘子可拆分为局部高介电常数结构和整体低介电常数结构。一方面需要改变盆式绝缘子几何形状；另一方面也需在绝缘子根部内嵌结构较为复杂的高介电常数区域。为了实现这一制造目标，尝试将成型精度高、制件缺陷少的光固化 3D 打印技术（Stereolithography Apparatus,SLA）[21]与传统热固化浇注工艺相结合，制备带有局部高介电区域的盆式绝缘子。

上述制备工艺的主要流程如图11a 所示。具体针对小尺寸绝缘件，可采用整体3D 打印并在内部预留局部浇注空间的方式制备。而对于大尺寸制件，可将预先打印好的高介电局部结构内嵌至小型化绝缘子模具当中，浇注环氧树脂已包覆上介电梯度结构，固化后实现全尺寸、小型化的绝缘子的制备，从而兼顾制造效率和电场优化效果。图11b 为通过 SLA 工艺制备的小型化盆式绝缘子的局部和整体结构，支持了上述方案的可行性。

图11 小型化绝缘子制造流程及3D 打印缩比绝缘结构 Fig.11 Fabrication procedure of downsized spacer and 3D printed down-scaled insulation structure

4 结论

1）提出了盆式绝缘子外法兰附近介电梯度结构的拓扑优化方法，发现减小密度函数指数因子m、减小梯度惩罚项权重系数q、增大介电常数上限εmax，有利于加快拓扑优化算法的收敛速度，获得更优的介电常数空间分布及更好的电场优化效果。

2）通过在盆式绝缘子根部设置近似菱形的高介电区域，可替代传统焊接工艺生产的“R 弧”金属屏蔽，使得沿面电场呈现理想的倒“U”型分布。此外，小型化改造绝缘子还能起到节约绝缘气体，缩小设备体积和占地，降低绝缘与金属材料的消耗的目的。

3）提出采用立体光固化3D 打印制备高介电常数局部结构，结合传统的热固化整体浇注工艺，有望实现高耐电性能、小型化盆式绝缘子的全尺寸制造，推动其实际工程的应用。

本文研究能够为GIS/GIL 等气体绝缘开关设备/输电管道中的盆式绝缘子结构优化、材料改性以及小型化改造提供指导。后续研究拟尝试制备本文中的小型化绝缘部件，开展绝缘部件电气性能和热/力学性能的试验分析，验证本文中小型化盆式绝缘子的应用效果。

需要指出，绝缘子表面金属微粒是GIS 设备发生故障的的重要原因[22-24]，且相较于高压电极的强电场区域，金属微粒更易出现在绝缘子表面靠近外壳腔壁的弱电场区[25-29]，因此，介电梯度的引入能否对表面金属微粒的电场畸变起到抑制，在后续研究中应予以重点关注。同时，介电梯度的理念以及梯度优化方法亦可拓展至直流电压工况下，通过介电常数或者电导率的梯度分布优化，实现表面电荷积聚特性的调控和沿面耐电强度的有效提升[28-30]。