温度与加载应力对双轴取向聚甲基丙烯酸甲酯蠕变行为的影响
丁 尧,张晓雯,郑梦瑶,相 宁,颜 悦
(北京航空材料研究院北京市先进运载系统结构透明件工程技术研究中心,北京 100095)
YB-DM-11 航空有机玻璃因其具有优异的光学性能和力学性能,被广泛应用于飞机座舱盖透明件。YB-DM-11 航空有机玻璃板材以浇铸板材为基础,经热拉伸和平面机械研磨抛光而成,高分子链段沿拉伸方向取向从而提高了有机玻璃板材的拉伸强度、断裂韧度与冲击性能等力学性能。定向有机玻璃成形是在加热和负载的情况下逐渐变形的过程,与材料的蠕变行为有密切的相关性。为了保证成形后制件的尺寸精度和力学性能,理解不同温度及外加载荷下YB-DM-11 航空有机玻璃的蠕变行为变得尤为重要。
蠕变是材料在一定外部载荷下,随时间推移而产生形变的过程。对于聚合物材料而言,蠕变在室温下就能发生,室温下的蠕变行为作为聚合物服役过程中的失效模式而备受广大学者关注和研究[1~5]。对于完整的蠕变过程描述并不多见,Cheriere 等[6]通过PMMA 不同温度的蠕变实验,得到了包含3 个阶段的蠕变曲线;Lee 等[7]在对PMMA 薄膜材料的蠕变实验中完整地观察到5 个蠕变阶段,但并未做出详细的描述。上述学者研究多集中于非取向态的有机玻璃,对于取向态的PMMA 蠕变行为的研究并不多见。为全面理解聚合物材料的蠕变行为,各种蠕变模型被用来揭示相应材料的蠕变响应。基于流变学理论,采用弹簧与黏壶的组合来描述非线性蠕变 行 为:广 义Kelvin-Voigt 模 型[8]、Burgers 四 元 件 模型[9]及修正的Burgers 模型、修正的Boltzmann 积分形式[10]等。通过相应的修正,在描述特定材料蠕变行为过程中得到准确性较高的拟合曲线。但对于此类模型由于其复杂的数学形式、较多的模型参数,导致了模型的可获得性较差;同时模型只针对特定材料具有较准确的拟合,并不具备普遍的适用性,在工程应用上并不多见。
为理解YB-DM-11 航空有机玻璃的蠕变行为,以及为进一步研究其成形机理提供定性的指导,本文在不同温度、加载应力条件下,研究了YB-DM-11航空有机玻璃的蠕变行为。对于蠕变过程中温度、加载应力对蠕变行为的影响方式进行详细的讨论,详细阐述了YB-DM-11 航空有机玻璃的蠕变行为的阶段性及各个阶段的微观机理。考虑到模型的准确性及工程应用,本文结合“广义方程”和“有效时间理论”[11]模拟YB-DM-11 航空有机玻璃的蠕变行为的前2 个阶段,通过拟合参数的物理意义揭示YB-DM-11 航空有机玻璃在不同蠕变条件下的物理状态,为分析不同蠕变条件对蠕变行为的影响提供参考。对于蠕变的后3 个阶段,由于其复杂性在本文中不做讨论。
1 实验部分
1.1 实验材料
YB-DM-11定向研磨有机玻璃(BO-PMMA):由锦西化工研究院生产,定向度为49%,板材厚度为9 mm。用机加的方法从有机玻璃板材中取样,将9 mm 板材铣薄至6 mm,并加工成哑铃形试样(参考标准ASTM-D638),表面经打磨抛光处理以去除机械加工带来的影响,试样尺寸如Fig.1 所示。

Fig.1 Tensile sample of BO-PMMA
1.2 测试与表征
1.2.1 拉伸性能测试:分别在25 ℃,100 ℃,105 ℃,
110 ℃,115 ℃,120 ℃下进行拉伸试验(标准参考ASTM-D638),拉伸速率为5 mm/min。试样尺寸如Fig.1 所示,厚度为6 mm。每个温度下至少重复3 次试验。开始测试前,试样在控温精度为±0.1 ℃的三度恒温箱中保温40 min,以保证试样温度均匀且达到测试环境温度。之后在Instron8800 单边加热疲劳试验机上进行测试,位移采用Epsilon 轴向引伸计测量,量程为-5~10 mm。
1.2.2 动态力学热分析(DMA):玻璃化转变温度采用美国TA 公司的Q800 型动态力学热分析仪,在双悬臂梁模式下对试样进行动态力学分析。试样长度为60 mm、厚度为2 mm,测试温度范围为20~180 ℃,升温速率为1 ℃/min,频率为1 Hz。玻璃化转变温度由储能模量曲线给出。
1.2.3 蠕变性能测试:采用Instron8800 单边加热疲劳试验机对BO-PMMA 进行拉伸蠕变测试(参考标准ASTM-D2990)。 试 验 温 度(100 ℃,105 ℃,110 ℃,115 ℃)低于玻璃化转变温度,加载速率1 MPa/s,蠕变试验至少进行14400 s(4 h)或超出设备最大量程(应变达到60%),每个条件下试验至少重复3 次。温度采用三度恒温箱控制,长期控温精度±0.1 ℃。试样尺寸与拉伸测试一致。加载前试样在恒温箱中保温40 min 保证试样温度均匀且达到环境温度。
2 结果与讨论
2.1 温度对BO-PMMA 拉伸性能的影响
Fig.2(a) 给 出 了BO- PMMA 分 别 在 25 ℃,100 ℃,105 ℃,110 ℃,115 ℃,120 ℃的拉伸应力应变曲线。从Fig.2(a)中可以看出,当温度从25℃升至115 ℃时,PMMA 的屈服强度从85.69 MPa 降至9.89 MPa,降幅达88%;温度继续升高到玻璃化转变温度120 ℃(由DMA 测得)时,PMMA 的屈服行为消失。Fig.2(b)给出了BO-PMMA 的屈服强度随温度的线性拟合曲线。拟合结果表明,随着试验温度的升高,BO-PMMA 的拉伸屈服强度呈线性下降规律。这是因为,室温下BO-PMMA 是高度取向的,链段运动被冻结。此时,分子运动的最小单元远小于链段,主要为链节或侧基运动;随着温度的上升,被冻结的链段运动逐渐解放,加速了PMMA 分子的热运动,同时高温导致分子链段发生松弛解取向,从而导致了材料屈服强度的降低。当温度达到玻璃化转变温度时,分子链产生整链运动,材料从玻璃态转变为橡胶态,此时屈服行为消失。

Fig.2 Tensile properties of BO-PMMA
2.2 BO-PMMA 拉伸蠕变行为
2.2.1 加载应力对BO-PMMA 拉伸蠕变行为的影响:基于2.1 节中BO-PMMA 拉伸试验结果,在保证蠕变应力不超过同等温度下屈服强度的前提下,对BO-PMMA 进行拉伸蠕变试验。BO-PMMA 在不同加载应力下的拉伸蠕变曲线见Fig.3。同一温度下,随着应力水平的增加,蠕变速率大幅提升,即相同时间内增加应力水平能得到更大的蠕变应变。这是因为外加载荷能有效地增加PMMA 的自由体积,使得分子链段的运动得以发生从而产生应变;或者说外加载荷降低了分子链段运动所需活化能,使得PMMA 发生形变;随着加载应力水平的提高,加速了PMMA 分子运动,从而导致蠕变速率随应力水平的增加而增加。

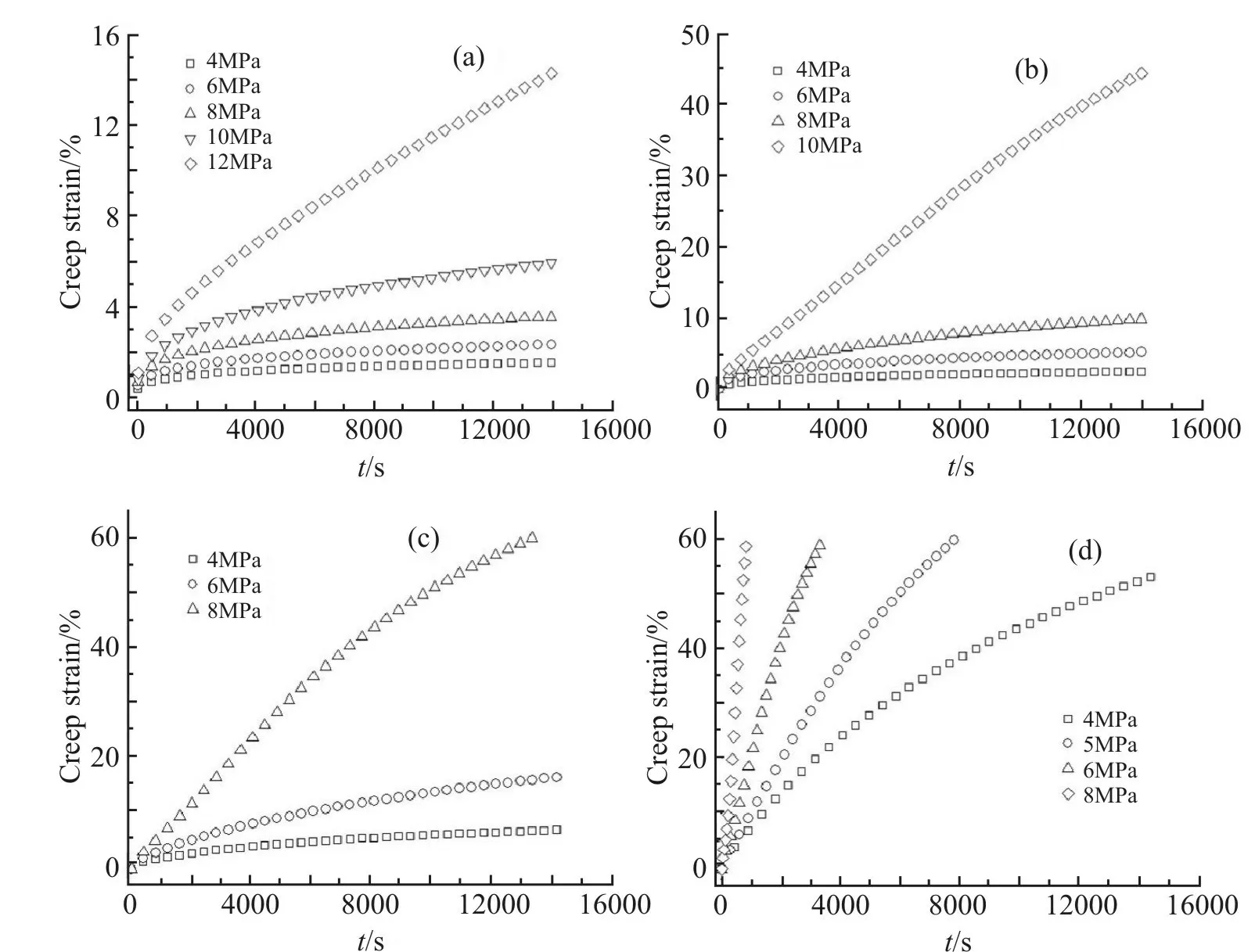
Fig.3 Isochronal creep curves at different stress

为揭示应力对蠕变各个阶段的影响,Fig.4(a)为115 ℃不同应力下蠕变速率随蠕变应变的演变。如图所示,应力为4 MPa 时,蠕变速率迅速减小,然后随时间逐渐趋于恒定,蠕变在相同的应变下保持在前2 个蠕变阶段;当应力大于4 MPa 时,蠕变速率出现了最大值,在相同的蠕变应变下,蠕变表现出完整的5 个阶段。这表明降低应力能有效地降低第2阶段、第4 阶段的蠕变速率,并且应力对第4 阶段蠕变速率的影响程度远远高于第2 阶段;当应力减小到4 MPa 时,第4 阶段的蠕变速率降低到与第2 阶段一致,此时蠕变的第3、第4 阶段消失,即蠕变仅仅表现出2 个阶段。
对于某一温度下,由于PMMA 分子取向产生的熵应力的松弛时间与加载应力有关,当加载应力较大时,迅速松弛的取向分子导致熵应力快速降低,从而蠕变第2 阶段持续较短的时间,如Fig.4(a)中,蠕变应力分别为5 MPa,6 MPa,8 MPa 时的蠕变速率曲线。当应力较低时,缓慢的松弛响应使得蠕变第2 阶段将持续较长的时间,在整个蠕变应变中保持稳定的蠕变速率,如Fig.4(a)中4 MPa 时的蠕变速率曲线。

Fig.4 (a) Creep rate curves at 115 ℃under different stresses; (b) strain and creep rate curve at 115 ℃and 8 MPa
蠕变行为在一定条件下表现出了复杂性,Fig.4(b) 为BO-PMMA 在115 ℃,8 MPa 下的蠕变及蠕变速率曲线,根据蠕变速率的演变可将其完整地划分为5 个阶段。在蠕变过程中,随着外加载荷的施加,有机玻璃在迅速施加的拉伸应力作用下分子链段迅速取向,导致蠕变第1 阶段的蠕变速率急剧下降。随分子链取向程度逐渐增加,取向态的PMMA 分子链段在熵的驱使下产生内部收缩的应力,当内部熵应力与外加应力平衡时,蠕变速率呈现出恒定状态,即蠕变的第2 阶段。随着时间的推移,PMMA 黏弹性松弛响应伴随着分子链解缠结、滑移甚至断链,导致其熵应力减弱无法与外加载荷持平,蠕变出现加速阶段即蠕变的第3 阶段。有学者将拉伸蠕变与等应变率拉伸试验对比,做出应力软化-蠕变第3 阶段等效假设(SSTCE)[14,15]:认为第3 阶段蠕变机理与等应变速率下的屈服后的应变软化一致。虽然未得到证实,但提供了一个可供研究的方向。对于聚合物材料蠕变的第4、第5 阶段的相关研究并不多见,对其机理的研究也未见发表。结合SSTCE 和蠕变过程的实验现象及应变速率响应,可以将蠕变第4、第5 阶段分别与等应变率的颈缩和取向硬化类比。
2.2.2 温度对BO-PMMA 拉伸蠕变行为的影响:Fig.5 给出了不同温度下BO-PMMA 在加载应力分别为4 MPa,6 MPa,8 MPa 时的蠕变等时曲线,在同等应力条件下,温度的升高急剧加速了蠕变速率。如Fig.5(a)所示,当加载应力为4 MPa 时,100 ℃和105 ℃的蠕变曲线基本重合,表明在较低应变水平下,蠕变行为表现出线性黏弹性;当蠕变温度达到110 ℃时,蠕变应变达到了7%,蠕变行为表现出非线性;随着温度的继续升高,蠕变速率急剧增加,非线性越来越明显。Fig.5(b),Fig.5(c)同样表明了BOPMMA 的非线性蠕变行为,升高温度与增加应力都使得BO-PMMA 蠕变行为表现出非线性。
与应力对BO-PMMA 蠕变行为的阶段性影响相似,如Fig.5(b)和Fig.5(c) 中,蠕变曲线随着温度的升高,蠕变行为从简单的2 个阶段到多个蠕变阶段。

Fig.5 Isochronal creep curves at different temperatures
Fig.6 给出了8 MPa 下温度对蠕变速率的影响(由于实验时长的限制,100 ℃,105 ℃蠕变应变未达到60%)。温度升高15 ℃,应变速率从6×10-6s-1到10-3s-1增加了近3 个数量级。同时温度降低使得蠕变第3 阶段逐渐消失,蠕变曲线变成仅由2 个阶段组成。
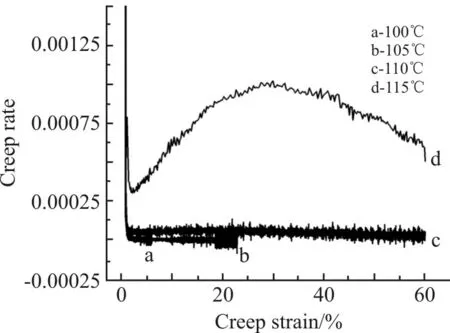
Fig.6 Creep rate at 8 MPa and different temperatures (creep rate curves at 100 ℃and 105 ℃almost coincide and are approximately zero)
综上可知,通过定性分析,温度与加载应力对BO-PMMA 蠕变行为的影响在趋势上基本一致,即BO-PMMA 的蠕变行为是由温度、加载应力耦合作用的结果,对于温度和加载应力对蠕变行为影响的定量分析正在做进一步研究。通过对温度、加载应力对BO-PMMA 蠕变行为的研究,有如下结论:蠕变达到第3 阶段时,与拉伸屈服相似,其分子链段产生解缠结、滑移甚至断链,导致成形后制品微观损伤。为了保证成形后制品的力学性能,改变蠕变条件使蠕变过程始终保持在第2 阶段能有效地消除蠕变第3 阶段产生的微观损伤。为此,下文结合蠕变模型,对蠕变前2 个阶段的温度、应力依赖性做了详细的讨论。
2.3 蠕变模型
为更深层次地理解蠕变过程中温度、加载应力对BO-PMMA 蠕变行为的影响,采用“广义方程”和“有效时间理论”[11]对BO-PMMA 蠕变曲线进行拟合。

式中:t0——实验前的老化时间,但在本实验中,并不存在具体的老化时间变量,因此在本实验中,t0代表由于不同蠕变条件带来的与老化等效的变量,称为等效老化因子。整个模型仅包含3 个参数,具有很好的工程应用价值。
Fig.7 给出了4 MPa、不同温度下BO-PMMA 的蠕变应变时间曲线及相应的拟合曲线。在100 ℃到113 ℃,模型均展现出较好的拟合效果;但在蠕变温度为115 ℃时,蠕变时间超过12000 s 后,拟合曲线与实验曲线出现一定的偏离,并且与实验数据之间的偏差越来越大,拟合曲线逐渐高于实验曲线。为了理解模型在较高温度下的失效原因,Tab.1 给出了模型拟合的相关参数。从表中可以得到,初始应变(ε0)随着温度升高呈上升趋势,因为温度升高有效地提高了材料的柔度,使得蠕变在初始位置有较大的蠕变应变。常数(B)为时间的修正系数。t0随温度的上升逐渐升高,当温度达到115 ℃时,t0出现下降趋势。115 ℃时拟合曲线高于该温度下的实验值,表明在接近玻璃化转变温度(Tg)=120 ℃时,等效时间理论逐渐失效。

Fig.7 Isochronal creep curves and fitting curves of 4 MPa by the universal formula and effective time theory (solid line)
Hodge[16]在描述聚合物的物理老化时指出,物理老化是玻璃态聚合物从非平衡态向平衡态的弛豫过程,该弛豫过程除了非线性之外,也是非指数的,并且表现出记忆效应,即特定状态下的弛豫不仅取决于该状态,还取决于达到该状态的过程。从Tab.1可以得到,t0随温度的升高而上升,这表明BOPMMA 试样经过高温定向拉伸后处于一个极不平衡的状态,温度的升高增加了分子活动性,从而增加了BO-PMMA 从非平衡态向平衡态的转化速率,所以老化参数t0随温度的升高而上升。但是温度对物理老化的影响是复杂的,在加速老化速率的同时也伴随着去老化过程[17],两者相互竞争。115 ℃时,t0突然下降,由拟合曲线与实验数据的偏离表明,115 ℃接近玻璃化转变温度(Tg= 120 ℃由DMA 测得),去老化速率逐渐增加削减了物理老化的影响,当温度高于玻璃化转变温度时,物理老化将被完全消除,t0将进一步下降,BO-PMMA 趋于回到定向拉伸前的状态。

Tab.1 Values of parameters obtained by fitting the creep curves
研究表明应力对物理老化同样有着加速作用[18]。因此应力对蠕变行为的影响也能用有效时间理论来反映。如Fig.8 所示,结合有效时间理论的广义方程对100 ℃不同应力水平BO-PMMA 蠕变曲线进行拟合,得到了高度一致的拟合曲线。Tab.2 给出了相关拟合参数,可见随着应力的增加,ε0逐渐增加,应力增加的材料的初始柔度,使得蠕变初始应变增加;等效老化因子(t0)随应力水平的增加而增加,表明应力加速了BO-PMMA 从非平衡态向平衡态的转变。蠕变过程往往伴随着损伤,并且蠕变损伤有着很强的应力、时间依赖性[19,20]。因此当应力水平较低时,蠕变损伤较小几乎可以忽略不计;但随着应力的增加及蠕变时间延长,蠕变损伤逐渐增加,因此未考虑蠕变损伤的拟合曲线在较长的时间尺度上逐渐低于实验曲线,这也是Fig.8 中12 MPa时,13000 s 之后实验曲线逐渐高于拟合曲线的原因。
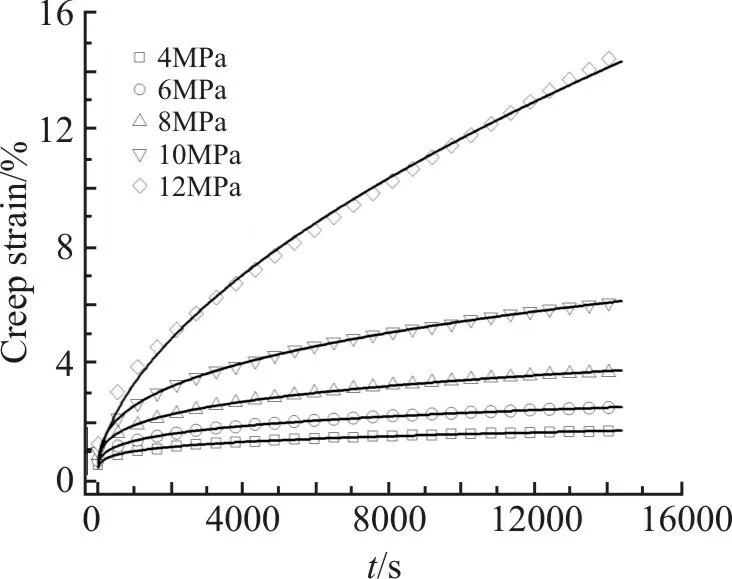
Fig.8 Isochronal creep curves and fitting curves of 100 ℃by the universal formula and effective time theory(solid line)

Tab.2 Values of parameters obtained by fitting the creep curves
综上所述,采用广义蠕变方程和有效时间理论对BO-PMMA 前2 个阶段蠕变行为的拟合得到较好的拟合效果,随着蠕变应力水平的增加或温度的提升,蠕变逐渐表现出多个不同的蠕变阶段,此时结合有效时间理论的广义方程将不再适用,需要新的蠕变模型去描述多阶段的蠕变形为,这已超过本文的关注点,在此不做讨论。
3 结论
(1)BO-PMMA 的屈服强度及屈服应变随温度的升高呈线性下降。温度从25 ℃升高到115 ℃,屈服强度从85.69 MPa 下降到9.89 MPa,下降了近88%,当温度继续升高到材料的玻璃化转变温度(120 ℃)时,屈服行为消失。

(3)BO-PMMA 在一定的条件下表现出5 个完整的蠕变阶段;通过降低蠕变温度或减小加载应力的方法可以降低第2、第4 阶段的蠕变速率,将BO-PMMA 的蠕变控制在前2 个阶段,即在所需应变下,通过调节温度或加载应力能有效减少蠕变过程中BO-PMMA 的损伤。
(4)针对BO-PMMA 蠕变行为,有效时间理论能给出较好的拟合曲线,同时揭示了蠕变温度与加载应力对BO-PMMA 蠕变行为的影响机制。

