面向FT‐M7002 的Sobel 边缘检测算法优化实现

范明亮，郭子涵，柴晓楠，商建东

（1.郑州大学 信息工程学院，郑州 450001；2.国家超级计算郑州中心，郑州 450001）

0 概述

随着大规模集成电路和信息技术的发展，数字信号处理器（Digital Signal Processor，DSP）受到广泛关注，DSP 具有高性能、低功耗等特点，可以满足图像处理实时性以及密集型计算的需求，因此，在图像处理领域得到大范围应用。目前，使用较多的高性能DSP 主要有TI 的C66X 系列，其片上集成8 个DSP 核心，单核浮点运算能力可达20 GFlops［1-2］。近年来，我国高性能DSP 的相关研究也取得了一定的成果，其中，由国防科技大学独立研制的FT-M7002性能较为突出。FT 处理器片上集成2 个DSP 核心和1 个CPU 核心，浮点运算能力达200 GFlops［3-4］。但是，在目前硬件发展较快的同时也显现出国产DSP平台缺乏相应软件支撑的问题。因此，对国产高性能DSP 处理器相应的软件环境以及函数库进行适配与调优，充分发挥国产DSP 的特殊硬件架构优势具有重大意义。

边缘检测是图像处理和计算机视觉中的重要研究课题，其目的是识别出图像中那些亮度发生明显变化的点。目前，图像边缘检测［5］广泛应用于图像识别、医学影像处理、机器学习等［6-8］领域。传统边缘检测算子包括Roberts 算子、Sobel 算子、Canny 算子、Prewitt 算子等［9］。Sobel 算子因其耗时短、具有一定的抗噪性、边缘检测效果好而得到广泛应用。近年来，很多学者基于硬件特性对Sobel 算法进行改进，并取得了一定的成果。文献［10］基于FPGA 提出一种多核矩阵处理器，其采用同构多核结构使数据并行传输和运算。文献［11］基于CUDA 架构，根据GPU 的并行结构和硬件特点优化数据存储结构。文献［12］基于Zynq-7000 系列平台，将ARM 处理器与FPGA 组合起来并利用异构多核平台实现加速。但是，由于各平台体系结构存在差异性，导致上述优化算法并不适用于FT 系列的高性能DSP。

本文面向FT-M7002 高性能处理器，基于该平台特性对Sobel 边缘检测算法进行优化。具体地，分析Sobel 算法特性，判断其是否可以充分利用FT 平台架构进行优化，针对算法中密集型数据访存运算，使用向量化、循环展开等优化手段实现数据级并行性，以提高向量寄存器、向量运算部件等硬件的资源利用率。在此基础上，针对DMA 产生的数据传输开销，采用双缓冲区结构使得数据传输与数据计算实现并行，并设计对比实验来测试优化算法的正确性及检测性能。

1 Sobel算法原理与FT-M7002体系结构分析

1.1 Sobel 边缘检测算法

图像边缘即图像中灰度值变化剧烈的位置，梯度算子就是利用图像边缘灰度的突变来检测边缘［13］。Sobel 算子包含2 个3×3 的矩阵，分别对水平和垂直方向上的像素进行滑动检测。假设一副图像中的某个3×3 区域如图1 所示，则Sobel 算子水平和垂直梯度模板分别如图2（a）、图2（b）所示。

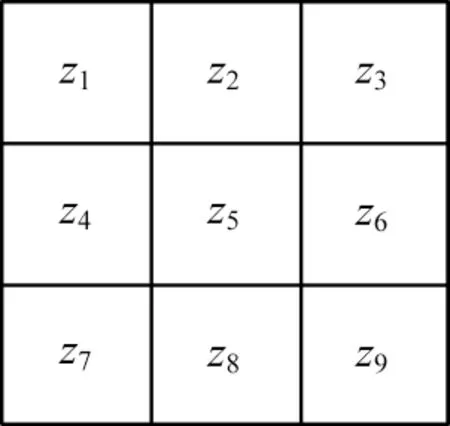
图1 3×3 区域示意图Fig.1 3×3 area schematic diagram

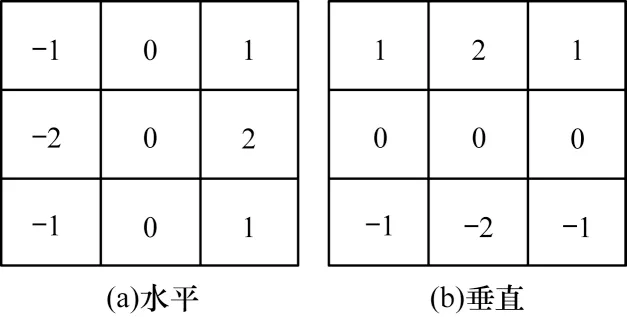
图2 Sobel 算子的水平和垂直梯度模板Fig.2 Horizontal and vertical gradient templates of Sobel operator

2 个二维梯度模板可以拆分为2 个一维卷积核，分别如下：

以X方向卷积模板为例，其中，[-1 0 1]卷积计算模板是为了计算X方向的差分，也就是得到可能的边缘点，而则用来平滑差分处理之后的像素，Y方向的横向和纵向卷积模板与X相同。根据上述2 个梯度模板，分别将其与图像像素做卷积计算，公式如下：

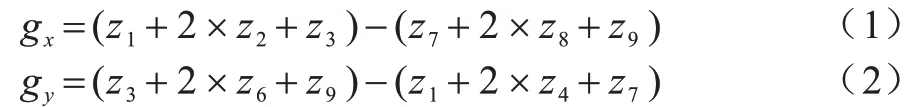
由式（1）、式（2）可以得到该点横向和纵向的亮度差分近似值，从而检测出横向和纵向的边缘。梯度向量的幅值和方向分别如下：

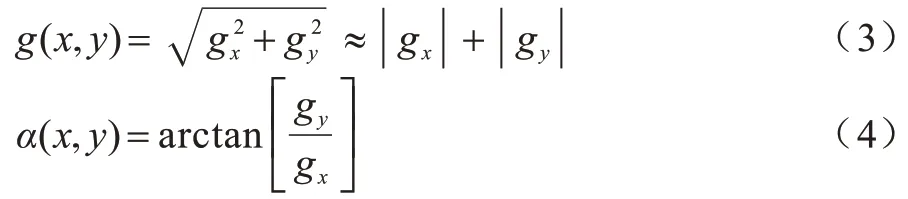
根据式（3）可以得到该像素梯度的近似值，最后选取合适的阈值，将计算得到的梯度近似值与阈值进行比较［14］，若梯度近似值大于阈值，则该点为图像的边缘点；否则，该点不是图像的边缘点［15-17］。由于Sobel算子对像素的位置影响做了加权，可以降低边缘模糊程度，因此其检测效果优于传统的Prewitt算子、Roberts算子。

1.2 FT-M7002 体系结构

FT-M7002 高性能DSP 芯片使用三级存储结构，单个计算核拥有32 KB 的一级数据缓存以及512 KB的向量存储空间（AM），所有计算核共享2 MB 的全局共享Cache，核外拥有32 GB 的大容量DDR 存储空间［18-21］。FT-MT2 内核基于超长指令字（VLIW）结构，包含一个五流出标量处理单元（SPU）以及六流出向量处理单元（VPU），2 个处理单元以紧耦合方式工作［22］。SPU 用于支持标量定点和浮点运算，主要负责数据的串行处理工作。VPU 内有16 个同构运算簇（VPE），负责对运算量大的密集型数据进行并行计算。直接存储访问（DMA）部件为内核提供了高速数据传输通路，通过配置传输参数启动对特定存储资源的访问，DMA 部件能够实现标量存储空间、向量存储空间与核外DDR 空间之间的数据交互。FT-MT2 内核结构如图3 所示。

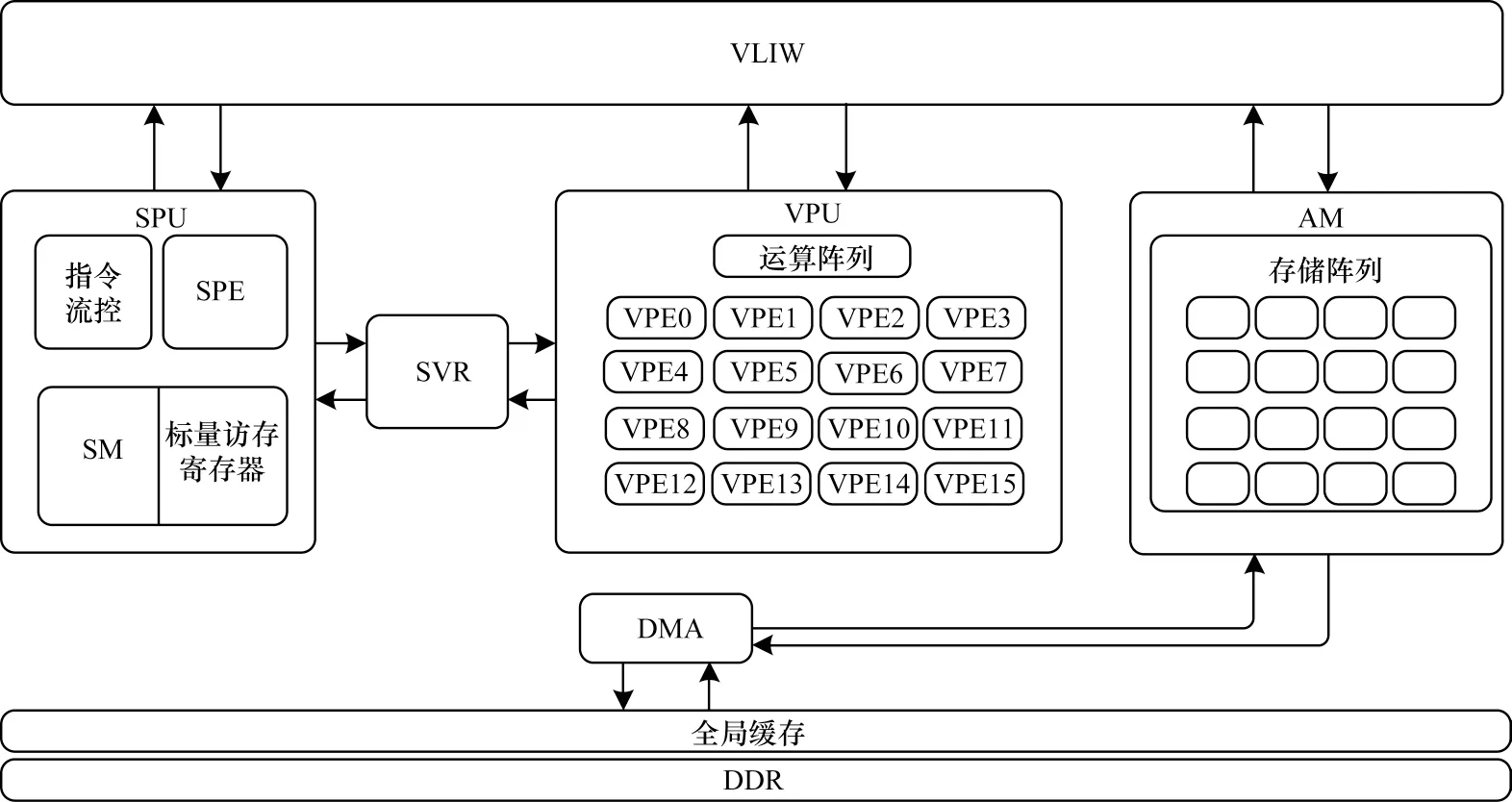
图3 FT-MT2 内核结构Fig.3 FT-MT2 kernel structure

VPE 内部集成的4 个运算部件可以支持标量定点和浮点运算，即该向量运算单元最多可以同时对16 路32 位数据进行向量运算并且支持混洗/归约操作。FT-M7002 特殊的体系结构为大宽度的向量运算提供了高效的数据存储及传输支持，能够在图像处理这种密集重复型计算中发挥优势。

2 基于FT-M7002 的Sobel 算法

2.1 算法实现

OpenCV 中通过获取Sobel边缘检测所需的卷积核进行梯度计算。Sobel 的实现是通过分离行卷积和列卷积来进行梯度计算，分别从X方向和Y方向对图片进行卷积操作，每个卷积方向又再次划分了横向卷积与纵向卷积，具体实现流程如图4 所示。在进行X方向卷积计算时，先将图像像素点与横向一维卷积模板相乘，然后再将计算之后的卷积结果与纵向一维卷积模板相乘，Y方向与之相同。使用分离的行、列卷积，能够在很大程度上减少计算量，同时又促进了对内存的连续访问。但是，当处理较大的图片时，内存访问量仍然是影响该算法性能的主要因素。

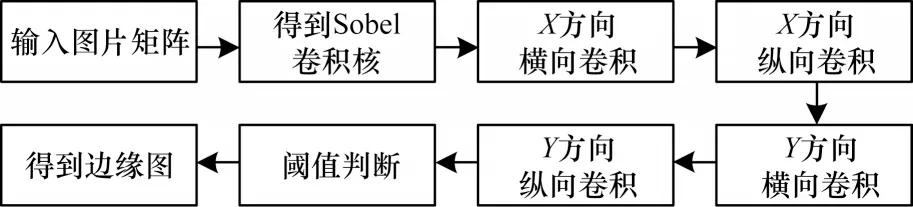
图4 Sobel 算法实现流程Fig.4 Sobel algorithm implementation procedure

2.2 算法优化

Sobel 边缘检测的主要计算过程是X方向卷积与Y方向卷积，本文先对其核心计算进行热点分析，发现该部分约占整体运行时间的1/2。因此，本文主要针对该核心计算部分使用SIMD 使其并行计算，充分利用FT 内核中的向量寄存器资源，减少卷积计算部分数据运算的访存次数，此外，利用DMA 传输机制设置双缓冲结构使数据运算与传输并行，最大程度地提高算法并行性，并通过FT 内部指令封装数据类型转换接口，从而扩展平台的兼容性。

2.2.1 向量并行优化

根据Sobel 核心计算部分的特性可知，计算过程存在数据连续访问、迭代次数多、计算量大等特点，而FT 处理器的内核向量计算特性可以很好地支持其使用SIMD 并行化。

核心计算位于循环体内，因此，首先针对循环体进行循环展开，选择适当的展开因子以保证代码体积不会过大，同时提高软件流水并行性，再利用FT内嵌的向量指令对计算过程进行向量化改写。首先，使用数据传输指令M7002_datatrans_cv 将内存中的图片数据传输到向量地址空间，通过vec_svbcast将这些数据从标量空间广播到向量空间；然后，利用vec_ld 指令从向量空间连续取出16 个数据，使用vec_add、vec_muli 每次可以完成16 个输入数据的乘加操作，计算完成后将结果保存到向量空间；最后，将结果传输回向量地址空间。以3×3 核的行卷积为例，具体核心计算部分代码如下：

2.2.2 DMA 传输优化

在Sobel 进行卷积的实际操作中，输入图片对应的矩阵规模一般大于向量存储空间，因此，输入数据需暂时置于核外DDR 中，通过DMA 将DDR 内的数据传输到AM 中。

作为数据传输的“中转站”，DMA 的传输时间会影响整个算法的效率。为了提高传输速度，本文针对Sobel行卷积操作中的数据连续访存过程，采用双缓冲区传输结构，如图5 所示，将AM 空间分成AM0 和AM1 两部分。基于此模式，数据从核外DDR 中传入AM0 空间，在判断为有效数据之后开始计算，同时，DMA 将下一块数据传给AM1。当AM1中的数据开始计算时，AM0输出上一次的计算结果并启动新数据传输，即在DMA进行传输循环检测前将数据的运算与传输并行化，减少一部分运算时间，从而达到性能优化的目的。

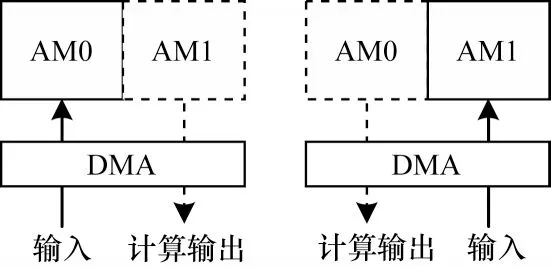
图5 双缓冲机制示意图Fig.5 Schematic diagram of double buffer mechanism

与行卷积数据传输过程不同的是，列卷积存在不连续的数据访问，无法通过向量指令进行连续存取。本文通过设置DMA 的目的索引值作为矩阵每行首元素的地址差，将行卷积矩阵中的每一行按列存储在矩阵中，最终实现矩阵转置。

2.2.3 数据类型转换

在图像处理库中，默认图片矩阵类型为8u（unsigned char），但是FT 向量处理器没有直接处理8u 类型的指令，针对该问题，本文利用VPE 内部混洗/规约等部件实现数据类型转换并封装成接口，从而实现unsigned char 和unsigned int 之间的相互转换，扩充FT 平台所支持数据的类型。

FT-M7002 向量寄存器可一次加载512 位数据到向量寄存器中。由于每个VPU 包含16 个VPE，因此每个VPE 中存放4 个unsigned char 类型数据，要转换成unsigned int 类型，即将每个VPE 中的4 个数据分别放入4 个VPE 中。如图6 所示，将每个原始VPE中的数据与0XFF 按位相与，即可得到新的VPE 中的数据存放，连续操作3 次就可实现数据转换。

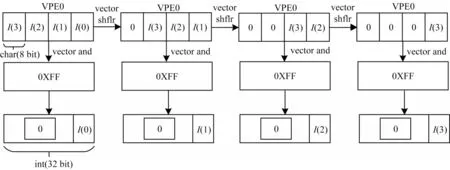
图6 char to int 类型转换（VPE0 实现）Fig.6 char to int type conversion（implementation of VPE0）

图6 只展示了VPE0 的实现，可以对VPU 中的VPE0～VPE15 分别做上述操作。值得注意的是，上述操作得到的数据并不是按序存放的，因此，需要对这些数据进行一次混洗（shuffle）操作，从而得到正确的数据排列方式。混洗单元通过合理配置混洗模式，可以实现VPE 中输入数据的按序存放。

3 实验结果与分析

本文以3×3、5×5、7×7 卷积核为例，分析不同尺寸输入图片对算法加速比的影响，同时将本文优化算法与TMS320C6678 中的Sobel 算法进行性能对比，以分析2 类处理器的单核计算能力。

3.1 实验环境

在飞腾平台的FT-M7002 开发板上实现Sobel 算法优化，调用定时器的计时函数来测试优化后程序段的执行时间，将FT-M7002 与TI 平台的高性能数字信号处理器TMS320C6678 进行对比分析。实验参数设置如表1 所示。

表1 实验平台参数设置Table 1 Experimental platform parameters setting

3.2 正确性分析

Sobel 边缘检测算法能在FT 平台上正确运行是算法优化的基础。为了验证优化算法的正确性，将不同尺寸大小的图片输入优化算法并运行于FT 平台，将其结果矩阵与OpenCV 图像库中Sobel 算法的结果矩阵进行对比，将2 个结果图片矩阵按像素点相减取绝对值，小于浮点数后6 位则认为结果正确。经验证，本文优化算法均能得到正确的处理结果。

3.3 性能分析

以Sobel 卷积核3×3、5×5、7×7 为例，分别以不同数据类型及尺寸的输入图片运行Sobel 串行算法和优化算法，在FT-M7002 处理器上的运行结果（时钟周期）如表2、表3 所示。从中可以看出，对于不同数据类型的输入矩阵，本文优化算法可取得1.66～3.14 倍的加速效果。加速效果整体趋势如图7、图8 所示，其中，横坐标表示输入矩阵规模，纵坐标表示本文优化算法相较串行算法所取得的加速比。

表2 8u 类型优化前后的性能比较Table 2 Performance comparison before and after 8u type optimization

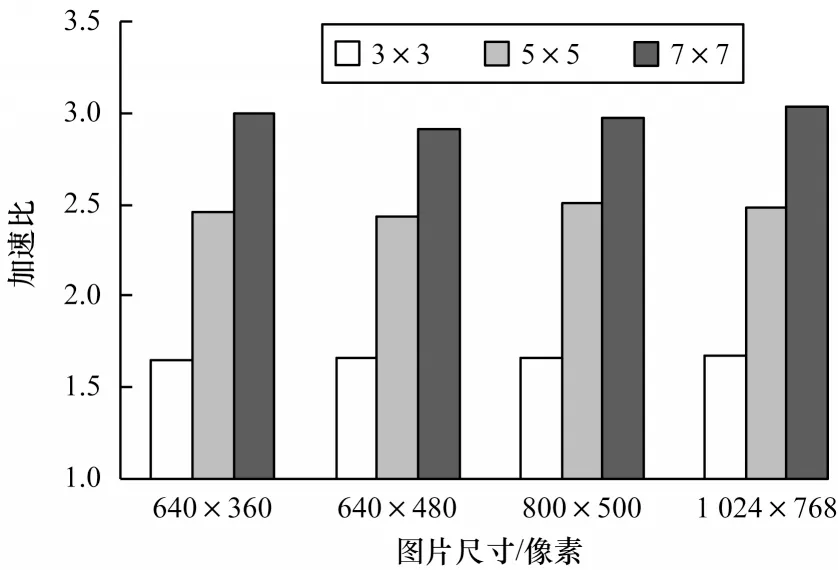
图8 32f 类型Sobel 优化算法相较串行算法的加速比Fig.8 The speedup ratio of 32f type Sobel optimization algorithm compared with serial algorithm

3.3.1 unsigned char 类型测试结果与分析

表2 所示为8u 类型不同矩阵规模分别在卷积核为3×3、5×5、7×7 上运行时的时钟周期以及加速比，图7 为其对应的加速效果柱状图。可以看出，整体加速比为1.75 左右，从趋势上来看，在同一输入矩阵规模下，随着卷积核的增大，计算量也在增大，加速比也增大；在卷积核一定的情况下，加速比随着矩阵规模的增大而缓慢增大，最后趋于平稳，这是因为数据存放在DDR 中，随着矩阵规模的增大，虽然使用了DMA 双缓冲结构，但是传输仍然耗时从而使得加速效果不明显，另外还需要进行数据类型转换，输入矩阵规模越大，类型转换也就越耗时。

3.3.2 float 类型测试结果与分析

表3 所示为float类型不同矩阵规模分别在卷积核为3×3、5×5、7×7 上运行时的时钟周期以及加速比，图8为其对应的加速效果柱状图。对比表2、表3可以看出，float类型的整体加速效果明显优于unsigned char类型，主要是因为FT 向量处理器可以直接处理float 类型的数据，不需要进行数据类型转换。对于不同的卷积核，核越大，加速效果越明显，这是因为随着核的不断增大，循环内每次计算的数据规模也就越大，因此，优化算法能更好地提升循环内数据的并行性。

3.3.3 平台对比分析

本次实验的对比测试所用图片为unsigned char 类型的三通道图片。在TMS320C6678中运行Sobel算法，在FT-M7002 中运行本文优化算法，分别使用TI 与FT平台的计时函数记录运行时间，FT 时钟周期换算为TI时钟周期时需要乘16。测试结果如表4 所示，整体加速效果如图9 所示。从中可以看出，对于不同大小的图片矩阵，FT-M7002 向量处理器比TI6678 多核处理器快了1.87～2.08 倍。因此，对于单核密集型运算，FT-M7002 平台相较TI6678 平台有一定的计算优势。

表4 FT 与TI 平台的比较Table 4 Comparison between FT and TI platforms

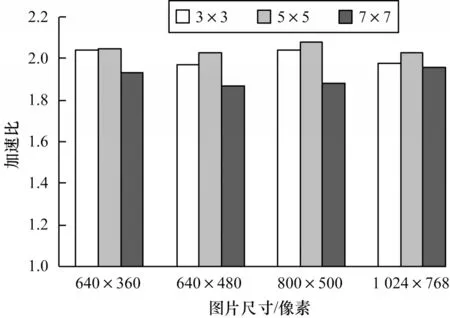
图9 FT-M7002 平台较TI6678 平台的加速比Fig.9 The speedup ratio of FT-M7002 platform compared with TI6678 platform

4 结束语

本文分析FT-M7002 硬件平台架构和Sobel边缘检测算法，基于FT内核结构特点对Sobel算法进行优化。为了充分发挥FT-M7002 平台的高性能计算特性，使用FT 内嵌指令对算法进行向量并行优化，利用循环展开的优化手段充分发掘数据级并行性。设计DMA 双缓冲区传输结构同步数据的传输与运算，对列卷积进行矩阵转置以解决其不能连续访存的不足。针对FT 平台向量部件不支持unsigned char类型访存操作的问题，设计相应的数据转换接口。对多种输入图片矩阵规模和卷积核大小进行对比测试，结果表明，在保证正确性的基础上，该优化算法相较串行算法获得了1.66～3.14倍的加速比，相较TMS320C6678处理器也取得了1.87～2.08 倍的加速效果，充分验证了本文所使用优化方法的有效性以及FT-M7002 平台的高性能计算优势。但是，本文目前仅针对单核进行了优化研究，下一步将探索多核优化问题，并在FT-M7002 平台上实现OpenCV图像算法库的整体优化。