基于最大最小距离的多中心数据综合增强方法

曹瑞阳，郭佑民，牛满宇

（兰州交通大学 机电技术研究所，兰州 730070）

0 概述

随着大数据技术的快速发展，以大数据为基础的数据分析方法进入了一个全新阶段［1］。在大数据环境下构建并训练的深度学习模型具有较优的性能。然而，数据量的缺乏［2-3］使得深度学习模型训练不充分，导致模型的泛化性能降低［4］。对于这种过拟合现象的发生［5］，正则化方法或简单收集更多的标记数据［6］能够增加数据量。此外，数据增强技术［7-8］通过特定的方法生成合成数据，通过对图像进行翻转［9-11］、旋转［12］、镜像［13］、高斯白噪声等技巧，实现数据增强，广泛应用于图像领域［14-15］。

在其他领域中也有相应的数据增强方法［16-17］。文献［18］采用随机设置部分信息缺失和增加噪声的方式对原有数据集进行扩充，在信息缺失和含噪声的情况下提高模型的鲁棒性，但是填充的数据量不好控制。如果填充的数据太少，则几乎不会改变原有数据集的分布，如果被扩充得太多，模型在该增强数据集下的检测效果呈现降低的趋势。文献［19］采用合成少数类过采样技术（Synthetic Minority Oversampling Technique，SMOTE）对少数类样本进行过采样操作，通过ENN（Edited Nearest Neighbor）算法剔除不符合要求的噪声数据。该方法能够有效解决数据不平衡所带来的问题。因SMOTE 算法存在一定的不足，多数类样本和少数类样本的边界出现模糊现象，使得检测的难度加大，甚至存在数据生成越界的问题。文献［20］通过时域重采样、能量变化、随机零填充这3 个步骤模拟数据，以提高模型的精确率，但是因对截止频率和重采样率有所限制，导致所产生模拟信号的多样性也受到了一定的限制。

现有的数据增强方法在时间序列分类方面的数据增强有限。文献［21］提出时间序列数据增强技术，能够有效解决数据增强在深度学习模型分类中存在的问题。在数据增强过程中，将所有训练集作为中心数据，延长模型的计算时间，同时由于某些中心数据选取不合适造成生成的新数据样本类别存在偏差，或者生成数据中心靠近边界，易受离散点的影响，导致生成数据越界现象的发生。在整个过程中固定近邻数k及权重函数，即生成数据所用样本的权重不变，在生成样本数据的多样性方面存在一定不足。

本文提出一种基于最大最小距离的多中心数据增强方法。通过加权密度减少离群点对最终结果的影响，将抽样方法与最大最小距离算法相结合得到多生成中心，避免了生成结果出现样本类别越界的情况。在此基础上，根据样本的相似性构建权重函数，计算加权平均得到新的样本，拓展样本数据的多样性。

1 基本概念

1.1 最大最小距离准则

最大最小距离准则［22］是基于欧氏距离，在最大程度上选取尽可能远的样本点作为生成中心，从而避免产生初始中心过于近邻的情况。数据生成类别越界示意图如图1 所示。

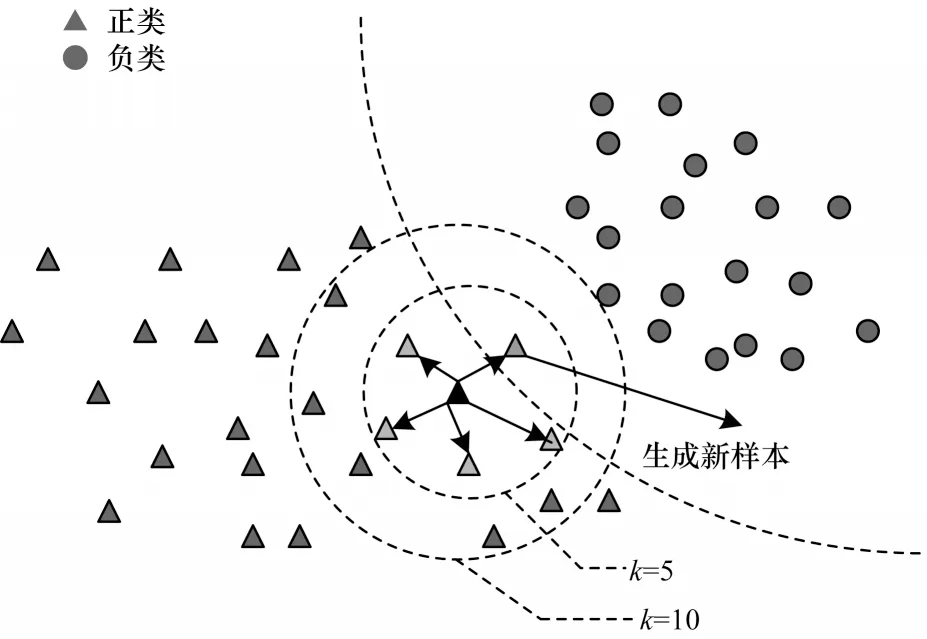
图1 数据生成类别越界示意图Fig.1 Schematic diagram of data generation categories transgression

最大最小距离算法的基本原理是首先从样本中选择1个任意样本点v1，并将其作为数据生成中心，选择距离v1最远的样本点v2作为另一个生成中心，然后再选择剩余l(l>2)时的中心点，分别计算剩余样本点到之前中心点的欧氏距离，将距离最小值依次放入集合中，同时下一个中心点为集合中最大值所对应的样本点，以此重复计算剩余所需要的中心点，过程如式（1）所示：

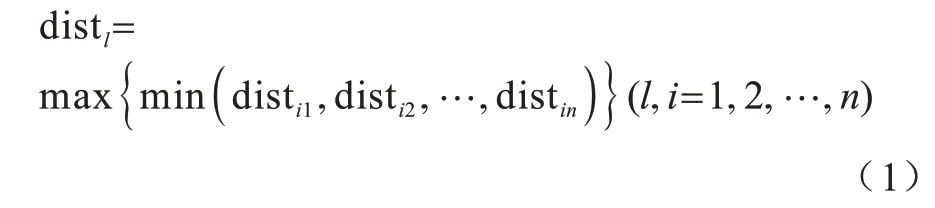
其中：disti1和disti2分别为样本i到v1和v2的欧氏距离。

1.2 最大最小距离算法改进

最大最小距离算法可以有效地解决数据生成中心处于边界的问题，从而避免出现生成样本越界的情况。传统SMOTE 算法对少数类样本进行分析和模拟后，在其近邻进行随机线性插值。如果该少数类样本位于边界处，那么随机生成的新样本就有可能出现越界的情况，而引入最大最小距离准则会重新选择生成中心。在第1 次计算过程中选取了最大的距离，在之后的计算过程中生成中心会向更小的距离接近，使得最远少数类样本点成为生成中心范围的边界，从而将最远边界控制在最远的少数类样本点之内，使得生成中心始终不会出现越界的情况，同时也带来了最大最小距离算法自身的缺点。最大最小距离算法在运行过程中要遍历两遍数据库，如果数据库很大，那么需要的计算时间将会延长。针对上述问题，本文考虑将抽样方法与最大最小距离算法相结合，通过简单随机抽样方法［23］提取原始数据库的主要特征，采用最大最小距离算法从抽样后的数据集中选取数据生成中心G1，重复该步骤得到生成中心G1，G2，…，Gn，经过多次抽样后得到多中心的数据生成中心集合G。原始数据集采样过程示意图如图2 所示。

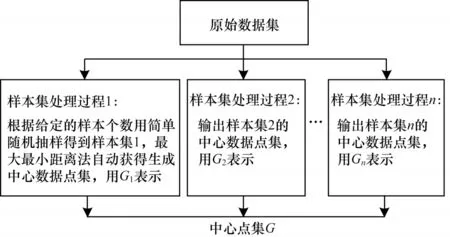
图2 原始数据集采样过程Fig.2 Sampling process of original dataset

设数据库的规模个数为105，直接采用最大最小距离算法对数据库进行计算，所需计算次数为2k×105。假设样本集的大小为103，采用最大最小距离算法对单个样本集进行计算，计算次数为2k×103。如果进行10次抽样，则共需的计算次数为2k×104，计算次数仅为前者的1/10。

简单随机抽样使得每个对象在总体中被抽到的概率相等，且每个样本集的数据生成中心点集都不同，极大丰富了数据的随机性和多样性。如果随机性过高会导致抽样样本分布不均匀。为保证一定的抽样精度，简单随机抽样必须进行多次抽样。

1.3 DTW 算法

动态时间规整（Dynamic Time Warping，DTW）算法是一个典型的优化问题，可以衡量2 个不同长度的时间序列相似度。

DTW 对序列A和B定义为A=(a1，a2，…，am)和B=(b1，b2，…，bn)。动态规整路径W=(w1，w2，…，wk)，max(m，n)≤K≤m+n-1。其中：wk对应同步点(x，y)k，k=1，2，…，k；x表示序列A元素的索引；y表示序列B元素的索引。动态规整路径需满足A和B序列上所有元素的索引与规整路径相一致，且w1=(1，1)，wk=(m，n)。假如某路径已经处于同步点(x，y)之后，那么该路径下一步只能通过点(x+1，y)、(x，y+1)、(x+1，y+1)，满足条件的路径个数为指数。动态时间规整的目的是用最少的代价找出与目标最相近的路径，其表达式如式（2）所示：

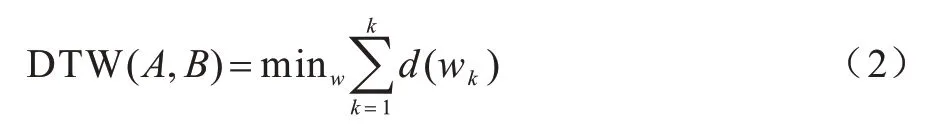
最小代价路径可以通过累计距离来计算得到，累积距离如式（3）所示：

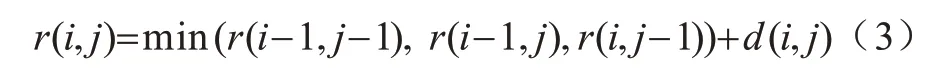
其中：d(x，y)为ax与by之间的距离。在该约束条件下最短的规整路径所对应的累计距离，便是所求2 个序列之间的DTW 距离。

2 本文方法

本文提出一种基于最大最小距离的数据增强方法MCA，基本原理是首先计算所有样本的加权密度，以排除离群点的影响，通过改进的最大最小距离算法得到中心点集G，尽可能保留有效特征；其次在每个备选中心点集中找出中心数据的k个近邻对近邻样本和非近邻样本进行赋权；最后利用加权算法计算选取样本的加权，以得到新的合成数据。

2.1 样本密度的计算

本文需要对各样本点的密度进行从大到小的排序，以减少MCA 方法的时间复杂度。样本xi的密度计算如式（4）和式（5）所示：

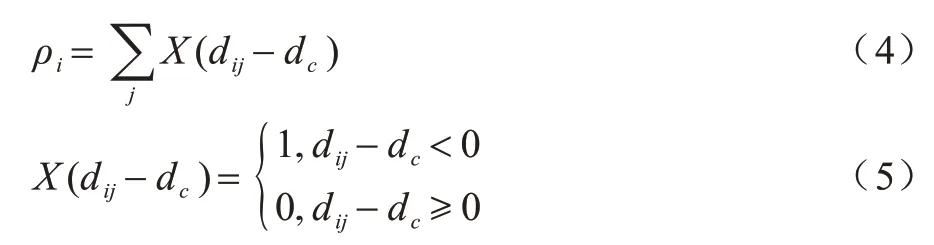
其中：dij为样本xi与样本xj之间的距离；dc为设置的阈值；ρi为落入以xi为圆心和以dc为半径的圆内样本数量。

2.2 所有样本点的平均距离

加权的欧氏距离如式（6）所示：

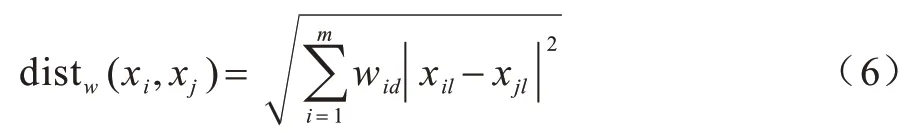
其中：distw(xi，xj)为样本xi和xj在m维空间下的加权欧氏距离；xil和xjl分别为在空间l维下的样本xi和xj；m、l为空间维数。

所有样本点的平均欧氏距离如式（7）所示：

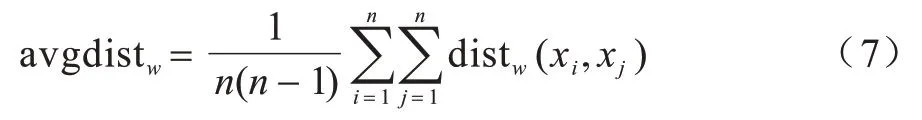
2.3 样本容量选择

本文从总体样本中抽取具有代表性的样本［24］，使得统计推断更加可靠。表1 是样本容量选取的参数。

表1 样本容量选取的参数Table 1 Parameters of sample size selection

在估算样本容量时需要给定抽样精度，一般用(α，ε)精度来表示，即在置信概率1-α下总体平均数的置信区间长度不超过2ε。在总体平均数的置信区间中，当n无限大时，近似服从正态分布，如式（8）和式（9）所示：

因此，当0<α<1 时，置信概率如式（10）所示：

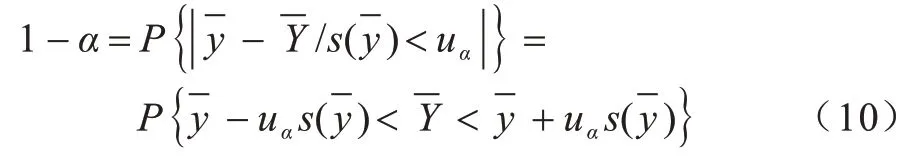
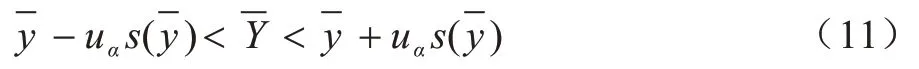
uα定义为：

其中：φ为标准正态分布N(0，1)的分布函数。

由式（11）可知，(α，ε)精度等价于：

由式（13）和式（14）可得：

因此，样本容量n的取值如式（16）所示：

在相同的总体容量中，用户可根据需求设定不同的置信区间和抽样误差。抽样误差和置信区间设置越小，所需的样本容量就越大。当总体容量增加超过一定阈值时，总体对样本容量的影响基本可以忽略不计。

2.4 权重选择

本文对权重进行赋值，选定时间序列T*和其最近邻，如果时间序列数据相对远离T*及其最近邻，则权重相对较低。本文随机选择一个中心时间序列T*，构建近邻相似权重，如式（17）所示：

虽然式（17）描述了连接Ti与T*的权重，但是未考虑Ti与T*的相关性，因此，相关权重的计算如式（18）所示：

其中：ne(T*)为Ti的k近邻。剩余样本权重的计算如式（19）所示：

其中：d*NN为T*与其近邻之间的最小距离。

2.5 MCA 方法流程

MCA 方法将样本集X 作为输入，数据增强后的数据集作为输出。MCA 方法流程如图3 所示，通过计算所有点的密度，剔除离群点，利用简单随机抽样获得小样本数据集，同时对小样本集运用最大最小距离算法得到生成中心，根据样本相似性构建权重函数，得到新的生成样本。

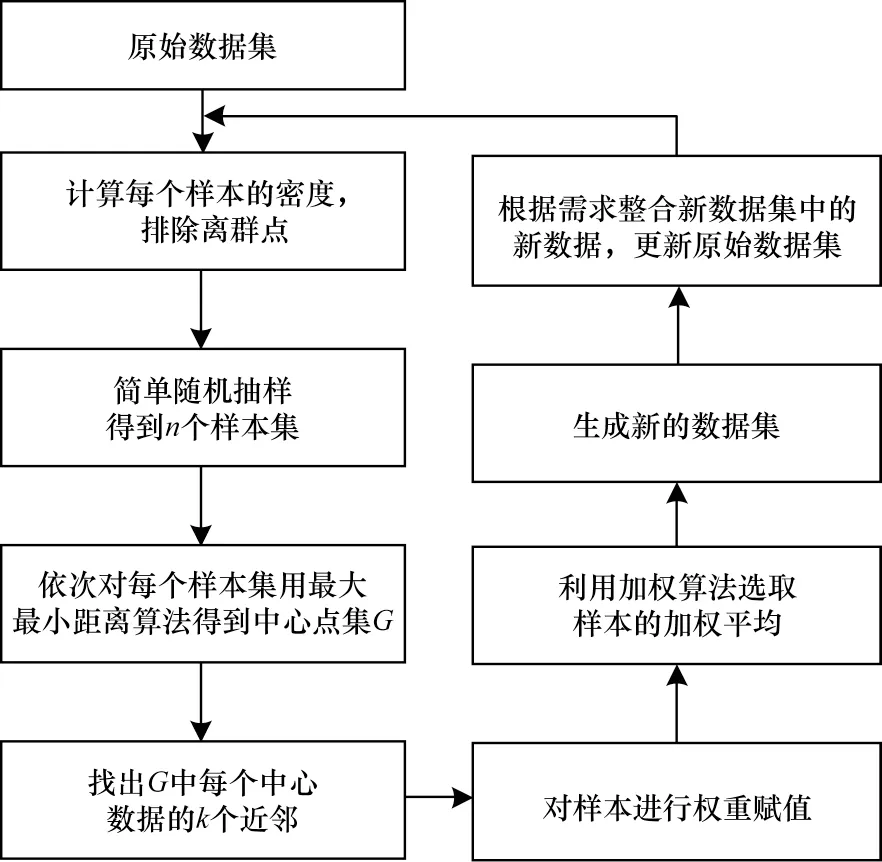
图3 MCA 方法流程Fig.3 Procedure of MCA method

2.6 深度残差网络

深度神经网络层数的加深不仅会导致出现过量的参数，还会引起网络退化。然而残差模块的引入就是为了解决网络退化的问题。深度残差网络［25］包括卷积层、池化层和全连接层等，其结构与深度神经网络结构类似。卷积层由含有若干可学习参数的卷积核构成，主要对局部信息进行计算，因此降低了计算量。池化层对主要信息进行降维处理，使原本高维计算变为低维数据的计算，有效地降低了计算量，在一定程度上避免了过拟合现象的发生。全连接层经过分类计算后，全连接层会对结果进行分类处理。

残差网络通过添加快捷连接作为恒等映射，使得网络性能不会退化。残差单元的示意图如图4所示。

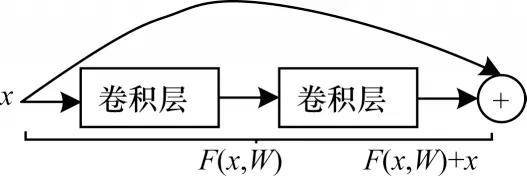
图4 残差单元示意图Fig.4 Schematic diagram of residual unit

图4 中残差单元的输入为x，残差单元中各层的参数为W。残差单元主要由2 个卷积层组成，这2 个卷积层的输出F（）表示需要学习的残差函数。跨层快捷连接和残差函数则共同构成残差单元的输出y，如式（20）和式（21）所示：

其中：σ（）为激活函数，选用线性整流单元（Rectified Linear Unit，ReLU）作为激活函数。激活函数使输入的线性组合变为非线性组合，从而解决模型梯度消失的问题，如式（22）所示：

ReLU 的输入为r，对应上一层网络的输出，ReLU 输出结果为r与0 的相对最大值。本文构建的深度残差网络用于检测生成数据的分类结果，其结构如图5 所示。

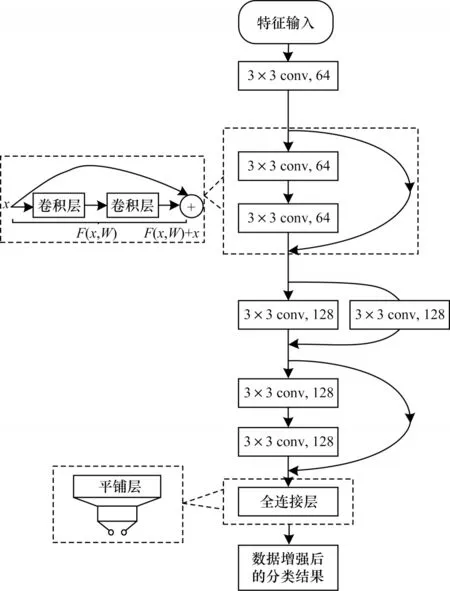
图5 深度残差网络结构Fig.5 Structure of deep residual network

从图5 可以看出，深度残差网络由卷积层、池化层和全连接层构成，激活函数为ReLU 函数，在一定程度上避免出现梯度消失的现象，且使得特征在层间传递时取值范围不变。深度残差网络采用Adma算法优化目标损失函数，其中基础学习率设置为0.1，衰减率为0.9，损失函数如式（23）所示：

其中：p为softmax 函数的输出概率值；y为样本的真实标签。在本文中，少数类样本标签为1，多数类样本标签为0。在实测数据集中轴箱振动异常样本的真实标签为1，无异常状态样本的真实标签为0。

3 实验结果与分析

3.1 数据集

为检测MCA 方法的性能，本文选取UCR 数据库中的SwedishLeaf 数据集和某高铁轴箱振动实测数据集进行实验。实测数据集为安装在高铁轴箱上振动传感器采集的数据，用于分析检测轨道平整度，同时选取领域内常用的过采样合成数据方法（SMOTE）、下采样的代表方法（Easy Ensemble）、随机简单复制样本（RR）、保结构过采样（INOS）、模型空间学习过采样（MK）及DTW 数据增强方法进行对比。数据集描述如表2 所示。

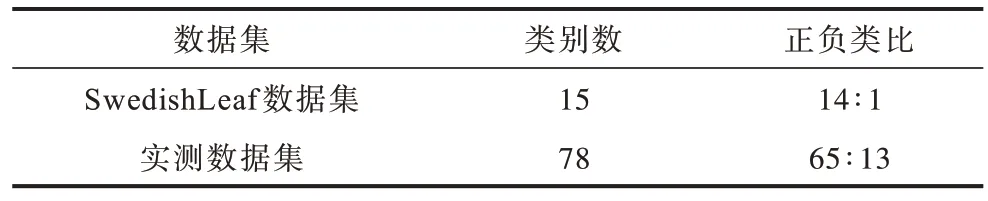
表2 数据集描述Table 2 Dataset description

3.2 实验环境

本文实验采用的软件配置为64 位window10 的操作系统，开发工具采用PyCharm 运行所提出的算法，运行环境为Intel®CoreTMi5-7200U CPU，2.50 GHz，8.00 GB。

3.3 样本容量的计算

样本容量是决定数据信息正确和计算效率的重要因素之一。样本容量越大，正确率越高，但效率会降低；样本容量越小，正确率越低，但效率会提高。本文对2.3节提出的公式进行定量分析，从SwedishLeaf 数据集中任选1 000 条数据，设置抽样误差为0.1，计算总体方差为0.368 2，利用式（16）计算在不同总体个数N发生变化时所对应的样本容量n的变化情况。样本容量计算结果如表3 所示。

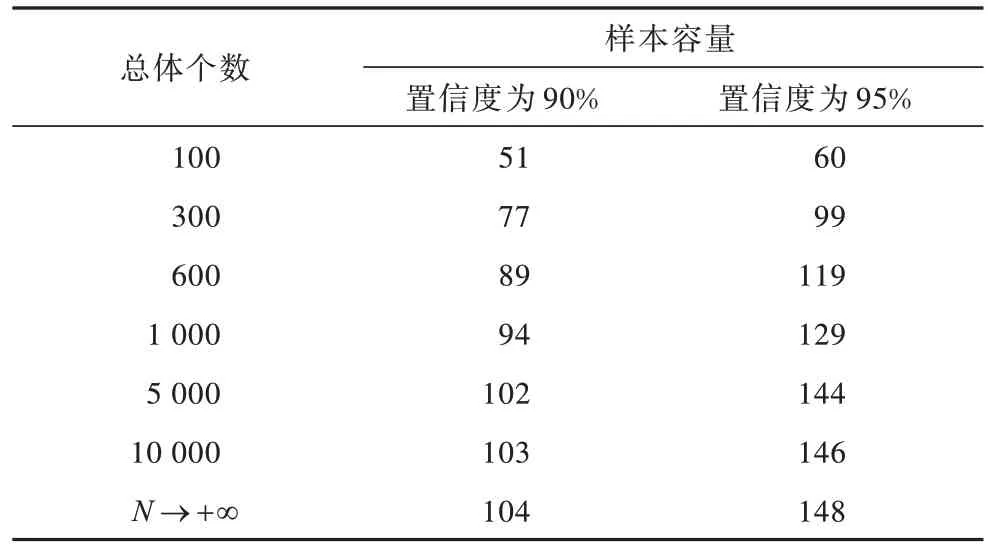
表3 样本容量计算结果Table 3 Calculation results of sample size

从表3 可以看出，在确定方差和抽样精度后，总体个数N越大，所需的样本容量n所占总体的比例越小。在置信度设置为90%的情况下，当N为100 时，n所占的比例约为51%；当N为600时，n所占的比例约为15%；当N为10 000 时，n所占的比例约为1%。在置信度设为95 的情况下，当N为100 时，n所占的比例约为60%；当N为600时，n所占的比例约为20%；当N为10 000时，n所占的比例约为1.5%。当置信度设置更高时，需要更多的样本容量来支持，抽样精度也需要相应的提高。当N达到一定阈值时，再增加N的量，n的增长呈现缓慢趋势。因此，超过一定阈值的总体个数对样本容量的影响趋向于0。

3.4 采样结果可视化

本文对不同的数据增强方法进行可视化分析，直观地展示采样后样本的分布情况。由于本文所采用的数据集维度较高，难以直接可视化，因此采取主成分分析（Principal Component Analysis，PCA）方法进行降维处理，选取贡献率排前2 的主成分，并在平面空间上进行结果可视化。在SwedishLeaf 数据集上时序采样可视化结果如图6 所示。实心点表示多数类样本，空心点表示少数类样本。

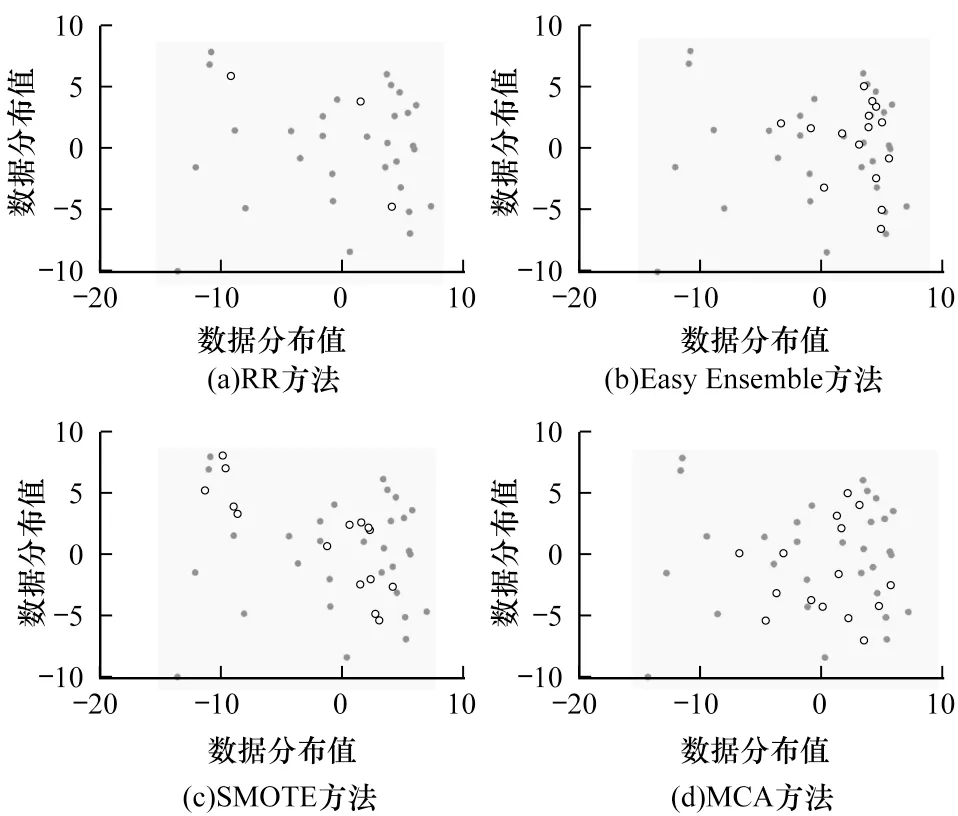
图6 时序采样可视化结果Fig.6 Visualization results of timing sampling

从图6 可以看出，SwedishLeaf 训练集由1 个少数类样本和14 个多数类样本组成，按照少数类和多数类1∶14 的关系随机选取30 条样本数据，并采用不同方法均生成15 个样本。不同方法的采样结果分析如下：

1）RR 方法仅通过随机复制少数类样本来平衡数据集，导致新生成的少数类样本与原少数类样本几乎完全重合。该方法对数据集信息量的扩充没有作用。

2）SMOTE 方法在原少数类样本周边均匀生成新的样本，生成的样本容易靠近边界，且在近邻选择时多数类样本和少数类样本的区别较模糊。

3）Easy Ensemble 方法剔除了信息量较少的数据，尽可能保留更多的有效信息，由于未考虑一些偏远点对结果的影响，生成的样本较原数据集中，缺少随机性。

4）本文提出的MCA 方法首先计算样本密度，排除噪声点的干扰，同时将最大最小距离算法与抽样方法相结合确定多生成中心，使得生成中心也远离边界，不会造成生成样本边缘化的问题，同时通过多次抽样提高样本的随机性，采用样本加权随机分配权重，使得生成样本序列多样性更丰富。

3.5 实验结果

在SwedishLeaf 数据集的少数类样本和多数类样本不平衡率（IR）下，不同方法的分类精度、召回率对比如图7 和图8 所示。

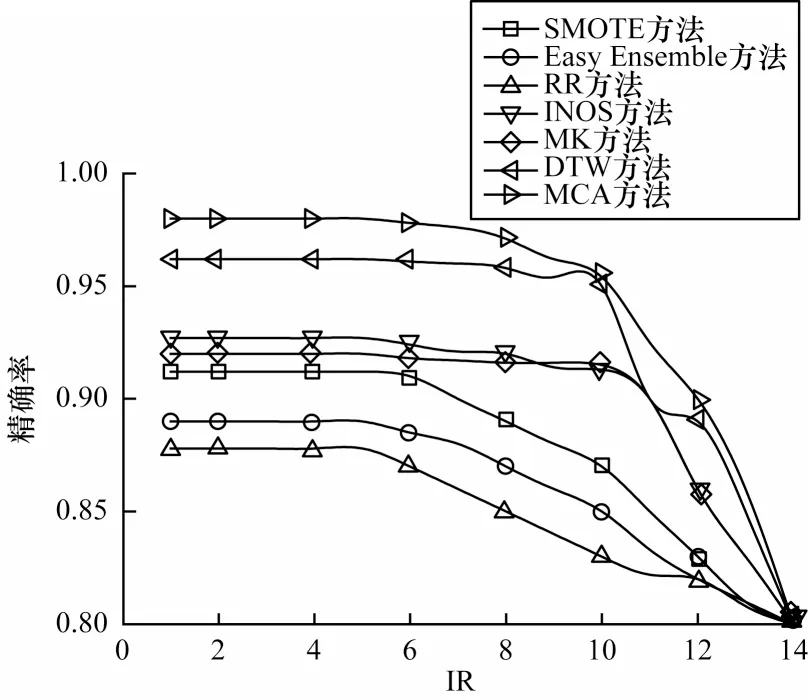
图7 在SwedishLeaf 数据集上不同方法的精确率对比Fig.7 Precision comparison among different methods on SwedishLeaf dataset

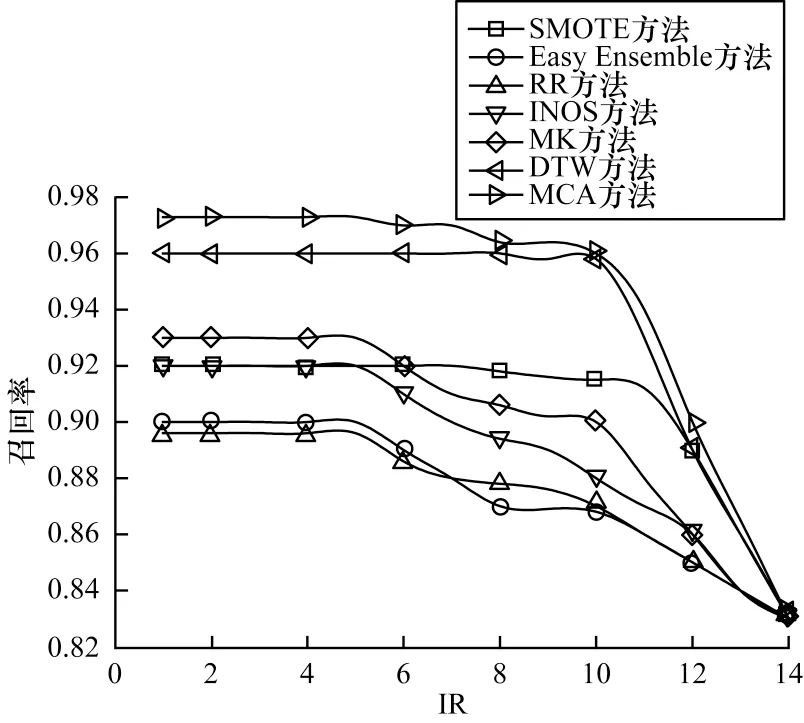
图8 在SwedishLeaf 数据集上不同方法的召回率对比Fig.8 Recall comparison among different methods on SwedishLeaf dataset

从图7 和图8 可以看出，在SwedishLeaf 数据集上，MCA 方法的精确率相较于其他6 种数据增强方法提高了7%～18%，召回率提高了4%～15%。MCA 数据增强方法较未进行增强前相比，精确度和召回率分别提高18%和15%，说明数据增强可以有效地提高数据集的分类准确度。相比SMOTE 方法，MCA 方法的精确率和召回率分别提高约6.7%和6%。SMOTE 方法只是在少数类样本周边生成新样本，未考虑整体样本的信息，在少数类样本的周围增加无用的噪声点，且可能出现样本越界的情况，从而影响分类结果。与Easy Ensemble方法相比，MCA 方法的精确率和召回率分别提高了约8.9%和8%。Easy Ensemble 方法采用降采样选取有效的样本子集，减少了整体数据量，导致模型训练量不够充分且整体数据量越小，降低了分类效果。相比RR、INOS、MK 方法，MCA 方法的精确率和召回率分别提高了5.9%和7%。RR 方法通过简单复制样本，生成的数据多样性较差，因此分类精度提升幅度较小。相比DTW 方法，MCA 方法精确率和召回率分别提高了约1.17%和2%。

为进一步验证MCA方法的有效性，在SwedishLeaf数据集上不同增强方法的F1 值对比如图9 所示。在相同的不平衡率下，MCA 方法的F1 值最高。在不平衡率较高的情况下，MCA 方法与其他方法相比提高了2%左右。

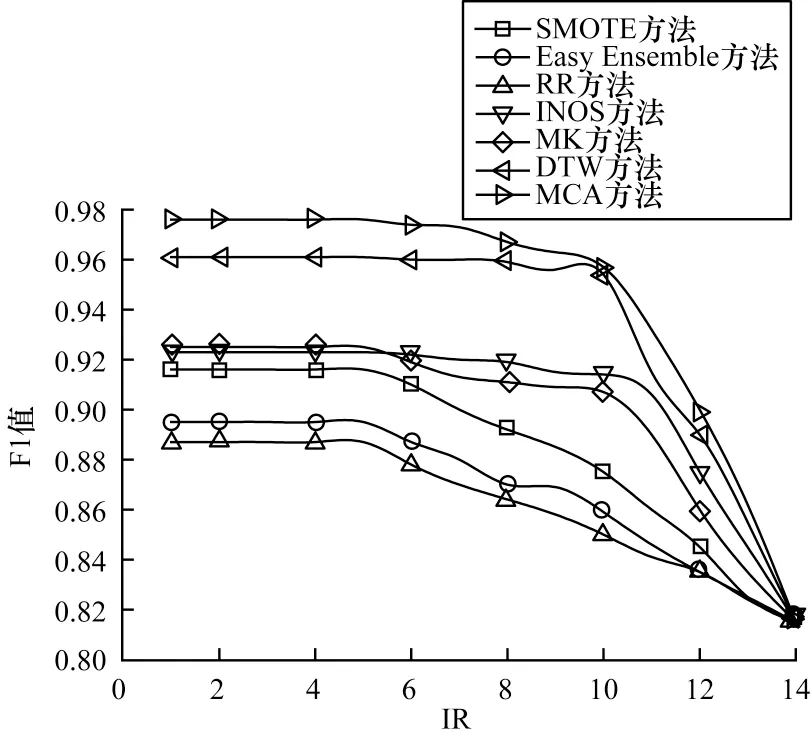
图9 在SwedishLeaf 数据集上不同方法的F1 值对比Fig.9 F1 values comparison among different methods on SwedishLeaf dataset

在实测数据集上MCA 方法与其他6 种方法的精确率和召回率对比如图10 和图11 所示。从图10和图11 可以看出，在实测数据集上MCA 方法与6 种数据增强方法相比，精确率、召回率均有大幅提升。相比Easy Ensemble、SMOTE 和RR 方法，MCA 方法的精确率提高5%左右，由于MCA 方法解决了生成数据样本类别越界的问题，提高了模型的训练准确率。MCA 方法与其他方法相比分类效果有很大提升，尤其是召回率提高了2%～6%。

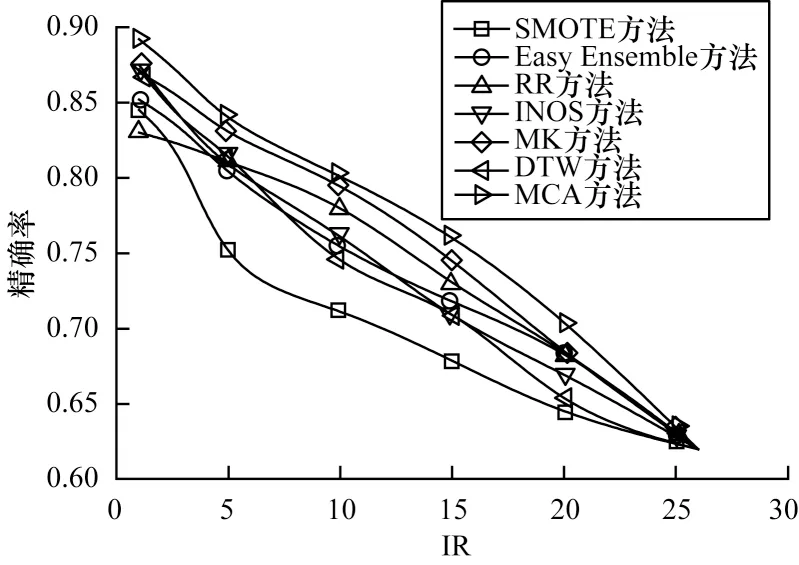
图10 在实测数据集上不同方法的精确率对比Fig.10 Precision comparison among different methods on measured dataset

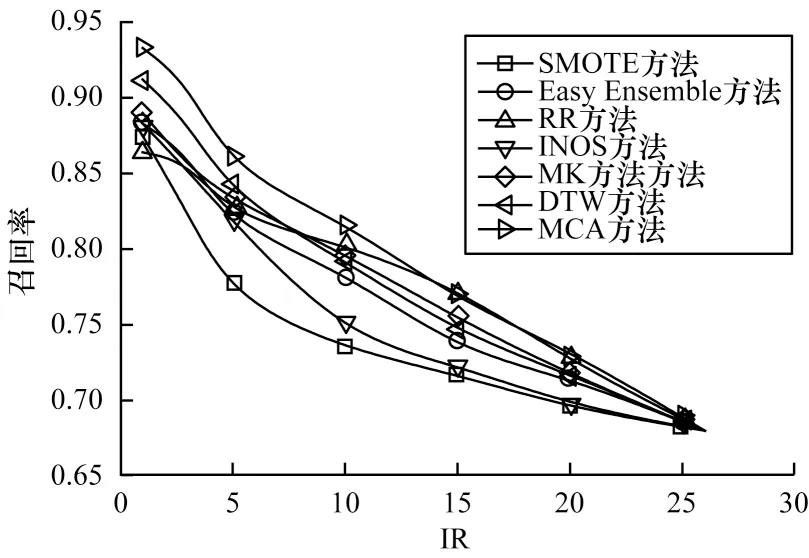
图11 在实测数据集上不同方法的召回率对比Fig.11 Recall comparison among different methods on measured dataset

在实测数据集上不同方法F1 值对比如图12 所示。从图12 可以看出，MCA 方法与其他方法相比F1 值提高了2%～5%，当不平衡率较大时，F1 值的提升速度最快，说明MCA 方法在不平衡率较大的数据集上仍具有较优的分类结果，适应不平衡数据的分类。

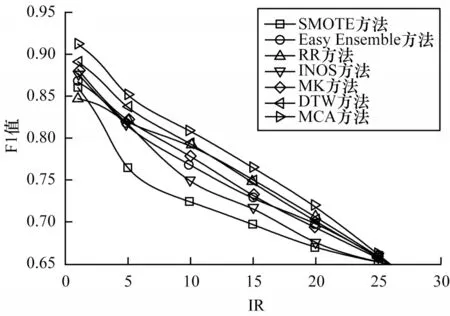
图12 在实测数据集上不同方法的F1 值对比Fig.12 F1 values comparison among different methods on measured dataset

4 结束语

本文提出一种基于最大最小距离的数据增强方法，通过考虑加权密度对排除离群点的影响，将抽样方法与最大最小距离算法相结合选取多中心，优化生成数据的中心，同时结合样本加权对多中心样本重新赋权，有效地增加生成数据的随机性。在UCR数据集和实测数据集上的实验结果表明，相比SMOTE、Easy Ensemble、RR 等方法，本文方法具有较高的精确率，并且在不平衡率较高的情况下具有较优的分类效果。下一步将通过对抽样方法和原始数据信息提取的问题进行研究，提高增强后数据集的分类精确度。