基于邻域聚合的实体对齐方法

谭元珍，李晓楠，李冠宇

（大连海事大学信息科学技术学院，辽宁大连 116026）

0 概述

随着智能信息服务应用的不断发展，知识图谱（Knowledge Graph，KG）已被广泛应用于智能问答［1］、智能信息处理［2-3］、个性化推荐［4］等领域。近年来，越来越多的知识图谱被构造以提供针对不同领域的知识，如DBpedia［5］、YAGO［6］、ConceptNet［7］、NELL［8］。研究人员发现，这些知识图谱通常不完整，相互之间包含着互补的事实，需要将不同的知识图谱整合到统一的知识图谱中，为不同的应用提供结构知识。然而，将来自不同知识图谱的实体链接到相同的真实世界知识并非易事，因为不同的知识图谱基于不同的数据源所构造，所以同一实体在不同的知识库中也有着不同的表述。

在多语言知识图谱中查找等效实体，对于集成多源知识图谱起到重要的作用。实体对齐（Entity Alignment，EA）旨在从来自多个来源构成的知识图谱中找到表示真实世界知识的同一实体。目前，比较流行的实体对齐方法是基于知识图谱嵌入的方法，此方法主要是利用知识图谱的表示学习，克服了依靠人工创建规则或特征［9］的问题。该类方法假定基于不同数据源构造的知识图谱具有相似的结构，在向量空间中具有相对相似位置的实体为对齐实体，使用TransE 等一系列模型［10-15］表示每个知识图谱中的实体和关系，然后将预对齐的实体投影至统一的向量空间。然而，基于知识图谱嵌入的实体对齐需要足够数量的种子序列，并且受不同知识图谱间不完整性和异质性的影响，对齐精确度往往不高。

图神经网络（Graph Neural Network，GNN）是学习图结构化数据的矢量表示和解决图上各种监督预测问题的强大模型［16-18］。GNN 遵循递归邻域聚合方法，每个节点聚合其邻居的特征向量以计算新的特征向量［16，18］。在聚合k次迭代之后，节点由其变换后的特征向量表示，该特征向量可以捕获节点多跳邻居附近的结构信息，然后通过合并来获得整个图的表示［19］。文献［20］证明，GNN 在识别同构子图方面具有与Weisfeiler-Leman（WL）检测［21］相同的表达能力。相似实体通常具有相似的邻域，这是GNN 实现不同知识图谱之间实体对齐的理论基础。

然而，现有基于GNN 的实体对齐模型依然面临着一个关键问题：由于不同的知识图谱具有结构异质性［22］，因此对应实体通常具有不同的邻域结构。解决此问题的关键在于要减小不同知识图谱实体邻域结构的异质性。本文提出一种邻域聚合匹配网络（Neighborhood Aggregation Matching Network，NAMN）模型，旨在从实体邻域角度对图结构信息进行编码以实现实体对齐，缓解结构异质性带来的影响。

1 相关工作

1.1 基于知识图谱嵌入的实体对齐

近年来，知识图谱嵌入学习已成功应用于实体对齐领域。当前的处理方法是将不同的知识图谱表示为嵌入，投影至同一向量空间，然后通过测量嵌入之间的相似性来进行实体对齐。MTransE［10］是基于嵌入的多语言实体对齐模型，其使用TransE 模型学习两个知识图谱中实体的嵌入，然后学习连接两个嵌入空间之间的映射函数，以实现实体对齐。IPTransE［11］和BootEA［12］是通过联合嵌入进行迭代的自我训练方法，其使用预对齐的实体种子对来进行计算，并将迭代过程中新发现的实体对添加到训练数据集中，优化对齐效果。JAPE［13］使用Skip-Gram方法，利用种子对齐方式将两个知识图谱的实体嵌入到统一的向量空间中，将结构嵌入和属性嵌入结合在一起找到相似实体。文献［14］提出了一种RSN 方法，结合递归神经网络（Recurrent Neural Network，RNN）和残差学习，以有效地捕获知识图谱内部和知识图谱之间的长期关系依赖性，优化实体对齐效果。MultiKE［15］分别从名称、属性和结构视图中学习实体的表示形式，集成3 个特定的视图嵌入组合策略以提高实体对齐性能，并使用预先训练好的词嵌入来完善属性值的学习。但是，以上方法需要足够数量的种子对，成本较高，并且不同知识图谱的结构异质性对知识图谱的嵌入质量也产生了很大的负面影响，导致对齐效果变差。

1.2 基于GNN 的实体对齐

与上述基于知识图谱嵌入的方法不同，图神经网络（GNN）使用图结构和节点特征来学习节点或整个图的表示向量，遵循邻域聚合策略，在图学习方面取得了显著进步。因此，一些工作试图将GNN 应用在实体对齐方面以取得更好的对齐性能。GCN-Align［16］是一种基于GCN 的实体对齐模型，其利用GCN 将每个知识图谱的实体嵌入统一的向量空间，传播来自邻居的信息，通过结构知识进行实体对齐。然而，GCN-Align 在训练过程中仅考虑实体之间的等效关系，没有在知识图谱中使用丰富的关系来区分共享邻居的实体。R-GCN［17］模型考虑到节点之间的关系，解决了GCN 处理图结构中关系对节点的影响，其通过为每个关系设置转换矩阵来进一步合并关系类型信息，提高对齐效果。RDGCN［18］是一种新的关系感知双图卷积网络，其通过构建用于嵌入学习的对偶关系图，使用门控机制捕获邻域结构，缓解知识图之间的异构性，以学习更好的实体表示。R-GCN 模型和RDGCN 模型将预先对齐的实体和关系作为训练数据，这可能会导致昂贵的开销。AliNet［23］模型将门控机制和注意力机制结合在一起，以聚合多跳邻域来整合GCN，从而减少图异构性对实体对齐的影响，达到更好的对齐效果。然而，AliNet 在汇总信息时将实体的所有一跳邻居同等对待，在没有仔细选择的情况下引入了噪声，影响了实体对齐性能。

2 NAMN 模型设计

2.1 基础知识

2.1.1 知识图谱的实体对齐

本文将知识图谱形式表示为Gi=(Ei，Ri，Ti)，其中，Ei、Ri、Ti分别表示为Gi中实体、关系和三元组的集合。Ne={e'|(e，r，e')∈T}∪{e'|(e'，r，e)∈T}是Gi中实体e的邻居集。对齐的实体对形式化表示为A={(e1，e2)∈E1×E2|e1↔e2}，其中，↔表示等价关系，即e1和e2所表示的为真实世界中相同的实体。实体对齐的任务就是找到G1和G2之间的等效实体对。为方便起见，本文将G1和G2放到一个大图中，即G=G1+G2，R=R1∪R2，T=T1∪T2，实体的总个数n=|E1|+|E2|。

2.1.2 图神经网络

GNN 通过递归聚合其邻居的特征向量来学习节点表示，不同的聚合策略产生了GNN 的不同变体，其中的一种变体vanilla GCN［24］在第l（l≥1）层处的节点i的隐藏表示为，如式（1）所示：

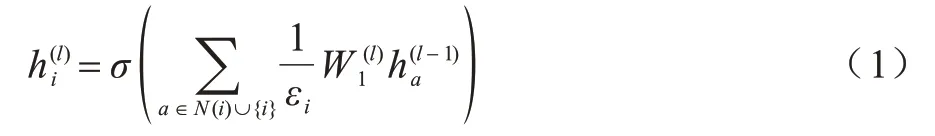
2.1.3 远距离邻居选择

为了减少邻域信息所带来的非同构影响，本文方法引入远距离邻居。如图1 所示，两个中心实体对（a，A）的一跳邻居不同，只包含对等实体对（b，B）和（c，C），而a的一跳邻居d和A的远距离邻居D对应，A的一跳邻居E和F与a的远距离邻居e和f对应。如果可以将远距离邻居e和f包含在a的邻域聚合中，并且也将A的远距离邻居D考虑在内，那么GNN 将会学习到更多关于a和A的相似表示。但是，并非所有的远距离邻居都有积极贡献，因此，本文引入注意力机制，旨在找到对中心实体有积极贡献的远距离邻域。

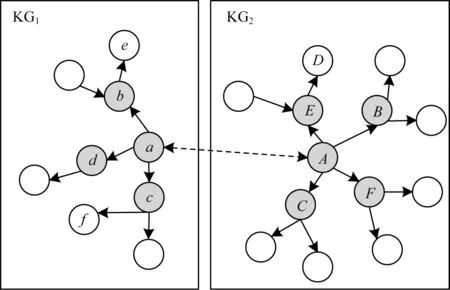
图1 远距离邻居选择示例Fig.1 Example of selecting long-distance neighbors

2.1.4 图匹配

通过图的结构信息来度量两个图的相似性，进而估计G1和G2描述的为同一实体的可能性。在近期研究中，图匹配网络（GMN）［25］引入跨图关注机制对图进行联合推理，以区分跨图的节点并识别差异，计算两个图之间的相似度得分。受GMN 模型的启发，本文也采用一跨图邻域匹配模块来识别两个实体邻域节点之间的差异。

2.1.5 距离函数

对于不同实体之间的相似性，通常采用计算实体之间的距离来度量，而计算距离的方法会直接关系到对齐的效果。表1 中列举了一些常见的距离函数。

表1 常见的距离函数Table 1 Common distance functions

2.2 NAMN 模型框架

为了缓解邻域异质性对实体对齐产生的影响，NAMN 模型利用GNN 对图结构信息进行建模，采用分层的思想对邻域信息进行区别处理。首先，对于一跳邻居进行全部采样，对于二跳及以上邻居，采用注意力机制进行局部采样；然后，引入门控机制对实体的k-hop 邻居信息进行聚合，以挖掘图结构的隐藏信息；在此基础上，考虑到实体一跳邻居结构异质性的影响，为每个实体提取一个可区分的邻域，构建邻域局部子图进行跨图邻域匹配，将匹配阶段的输出与通过门控机制所学习的图结构表示进行联合编码，以生成面向匹配的实体表示；最后，对于面向匹配的实体表示，使用距离函数进行实体的对齐预测。NAMN 模型框架如图2 所示，在不失一般性的情况下，该图展示了一跳和二跳邻居信息的情况。NAMN 遵循3 个阶段的处理流程，即门控邻域聚合、邻域匹配和对齐预测。

2.3 门控邻域聚合

按照每跳邻居对中心实体的重要性可知，实体的一跳邻居是最重要的邻域。本文使用vanilla GCN聚合实体的邻居信息，学习知识图谱结构嵌入。首先，使用预训练的词嵌入［26］来初始化GCN 的方法。将两个知识图谱G1=(E1，R1，T1)和G2=(E2，R2，T2)作为NAMN 模型的输入，使用式（1）来更新节点表示。为控制噪声的影响，还引入highway networks［27］方法，以避免噪声在GNN 层之间传播。

对于二跳邻居，若再直接采用GNN 层来聚合，会导致更多的噪声信息。为找到对中心实体有积极贡献的远距离邻域，本文引入注意力机制［23］来计算实体ei的二跳邻居信息（表示为），如式（2）所示：

其中：N2(·)代表的是实体的二跳邻居集合；W2是可训练的权重矩阵；βia是中心实体i与邻居a的一个可学习的注意力权重。

为进一步聚合邻域信息，使用门控机制将邻域信息结合在一起，以挖掘实体ei的隐藏表示：

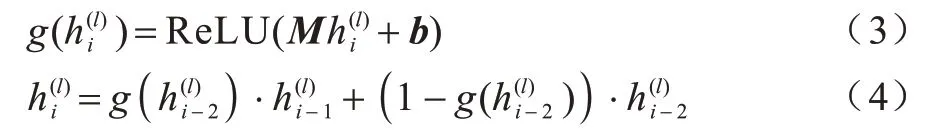
对于two-hop邻域聚合，本文引入注意力权重βia以突出重要邻居。图注意力网络（Graph Attention Network，GAT）［28］是在实体中采用共享的线性变换，但是却忽略了中心实体和邻居之间可能完全不同，这种共享的转换会导致无法正确区分。为此，本文分别使用两个矩阵M1和M2对中心实体和邻居进行线性变换［23］。形式上，中心实体i和邻居a之间的注意力权重计算方法如式（5）所示：

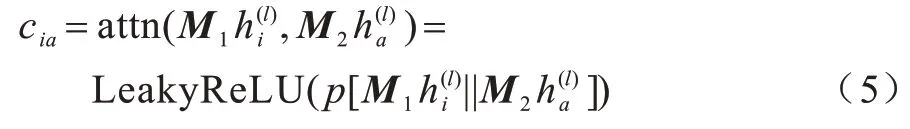
其中：p、M1和M2为可训练的参数；||表示级联；cia是衡量ei和ea重要性的注意力权重；attn(·)是注意力函数。在此基础上，使用softmax(·)函数进行标准化处理，以使其在不同实体之间具有可比性，从而有效地编码实体名称的语义信息：

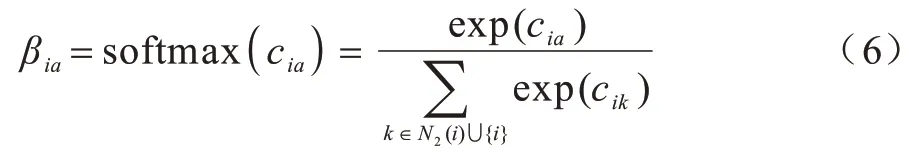
将两个知识图谱G1=(E1R1T1)和G2=(E2R2T2)作为NAMN 模型的输入，使用式（1）来更新节点表示。为控制噪声的影响，还引入highway networks［27］方法，以避免噪声GNN 层之间传播。

2.4 邻域匹配

2.4.1 邻域局部子图构建

实体的一跳邻居是决定该实体与其他实体是否对齐的关键，但是并非所有的一跳邻居都对实体对齐有着积极的影响。为此，本文引入局部子图，应用向下采样过程（down-sampling process），旨在选择对中心实体信息量最大的一跳邻居。对于每个实体对(ei，ej)，如果ei和ej有关系（例如r）直接连接，在局部子图中为其对应节点添加一有向边，但只保留r的方向。

为了选择合适的邻居，采用邻里采样策略［29］。给定实体ei，对其一跳邻居ei_1进行采样的概率如式（7）所示：

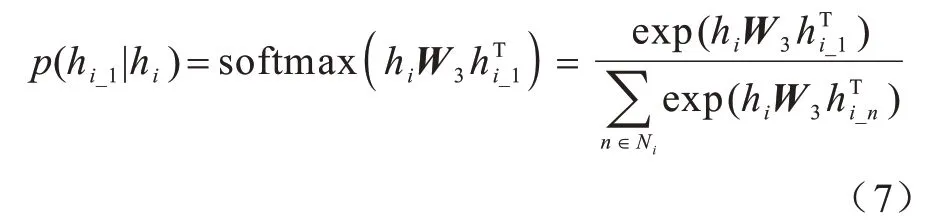
其中：W3是共享的权重矩阵；Ni是中心实体ei的一跳邻居集；hi和hi_1分别是中心实体ei和一跳邻居ei_1通过式（1）计算的学习嵌入表示。

2.4.2 跨图邻域匹配

确定对中心实体应考虑的邻居之后，也即产生了邻域局部子图。在跨图邻域匹配过程中，为减少匹配开销，首先进行的为候选人的选择。计算G1中的实体ei与G2中的所有实体{e2}在其表示空间中的相似性，找到G2在嵌入空间中最接近ei的实体，作为候选者，计算公式如式（8）～式（9）所示：

其中：sh是向量空间相似性度量，如Euclidean 或cosine；αij是注意力权重；p(hj|hi)为G2中的实体ej被采样为ei候选者的概率。

在邻域匹配模块中，G1和G2叠加在一起作为一个大的输入图，引入一匹配向量来计算G1中的实体邻域和G2中所有实体的匹配程度［25］。形式上，令(ei，)为要测量的实体对，其中ei∈E1，而∈E2为候选者之一，设定x和y分别是ei和的两个邻居，得到邻居x的匹配向量mx：

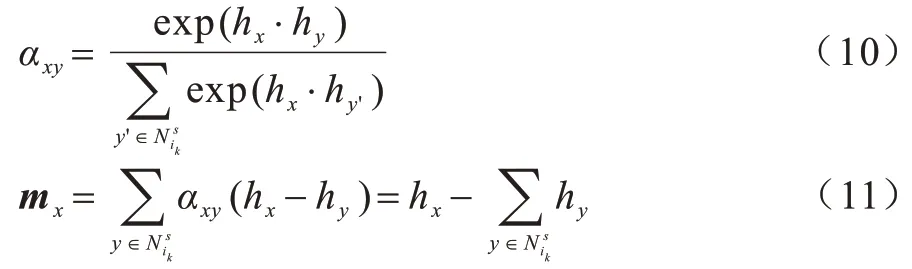
然后，将邻居x的输出嵌入与匹配向量相结合：

其中：τ是超参。此处，匹配向量mx可以区分两个邻居之间的差异。当两个邻居表示相似时，mx趋向于零向量；当邻居表示不同时，匹配向量mx将会变大。

其中：Wgate和WN分别是可学习的门控制矩阵和共享矩阵；是采样的邻居集。

2.5 对齐预测

对于最终生成的面向匹配的实体表示hmatch，可以简单地通过测量两个实体之间的距离来判定两个实体是否应该对齐：

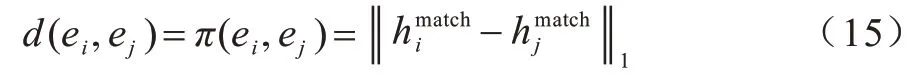
其中：||·||1表示L1范数。将基于边际的排名损失函数作为NAMN 模型的目标：

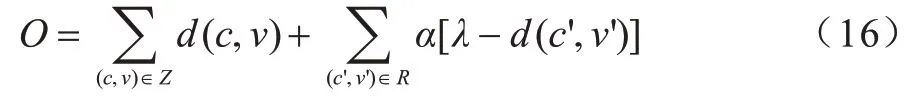
其中：c和v、Dc和Dv组成负样本的候选 集R={(c'，v')|(c'=c∩v'∈Dc)∪(v'=v∩c'∈Dv)}；Z是候选的种子集；α是平衡的超参数。本文目标是使对齐的实体具有很小的距离，未对齐实体表示具有较大的距离，即负样本的距离应该大于λ，也即d(c'，v')>λ。

此外，使用Adam 优化器［31］对目标进行优化，通过Xavier 初始化［11］对所有可学习的参数（包括实体的输入特征向量）进行初始化。

3 实验

3.1 数据集

为了评估NAMN 模型性能，参考最近的研究［12，32］，本文使用大型数据集DBpedia［33］下的子集DBP15K 作为实验数据进行验证。这些数据集包括3 个跨语言数据集，分别是英语、中文、日语和法语的不同语言版本，即DBP15KZH-EN（中文-英语）、DBP15KJA-EN（日语-英语）、DBP15KFR-EN（法语-英语），每个数据集由15 000 个对齐的实体对和约40 万个三元组组成。3 个数据集的详细信息如表2 所示。

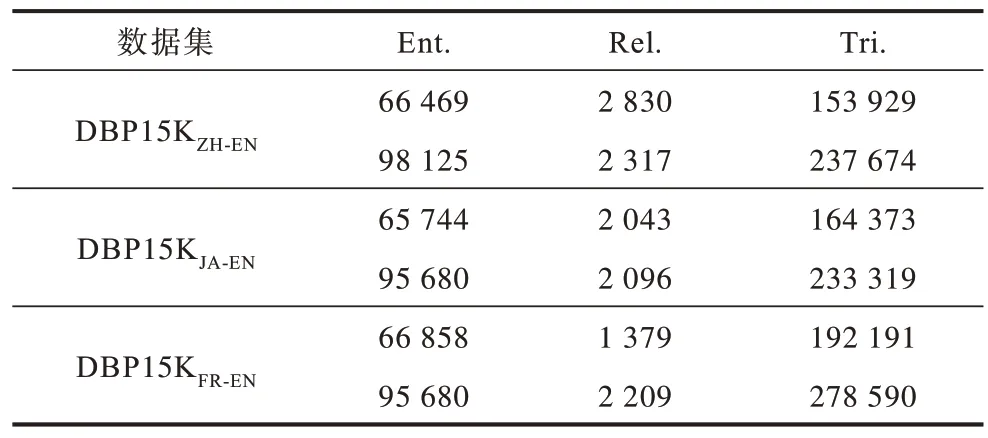
表2 数据集统计Table 2 Data set statistics

3.2 评估指标与参数设置

按照惯例，将数据集的30%作为训练数据，剩下的70%用作测试数据。在以下超参数中进行搜索：学习率Rlearning_rate={0.001，0.005，0.01}，τ={0.1，0.2，…，0.5}，α={0.01，0.05，…，0.1，0.2}，λ={1.5，1.4，…，1.0}，每层的隐藏层层数L={1，2，3，4}，维度为{100，200，300，400，500}，最终实验设置如表3 所示。此外，本文设置候选人的大小为20个，并为每个预先对齐的实体对抽取10个负样本，以简化训练。

表3 参数设置Table 3 Parameters setting

对于评估指标，使用Hits@K和平均倒数排名（Mean Reciprocal Rank，MMR）评估对齐性能。Hits@K通过排名在前K个的正确对齐实体的比例来进行计算，MRR 是指所有正确实体的平均倒数排名。这两个指标值越高，表明实体对齐模型效果越好。

3.3 对比方法与实验结果

本文将NAMN 模型与最近提出的基于嵌入的实体对齐模型进行比较，并将其分为2 类：1）基于嵌入的模型，如MTransE、IPTransE、JAPE、BootEA 和RSN；2）基于图的模型，如GCN-Align 和RDGCN。同时，引入近期考虑到知识图谱邻域异质性的两个最新成果进行比较，即MuGNN 和AliNet 模型。

表4 列出了在DBP15K 数据集上所有方法的实体对齐性能。实验结果表明，NAMN 明显优于3 个数据集上的所有基线模型。NAMN 模型可以实现Hits@1的所有值均高于75%，Hits@10 的所有值均高于85%，MRR 的所有值均不低于80%，这进一步证实了本文方法的有效性。具体来说，在基于嵌入模型中，BootEA模型表现最佳，通过引导过程可以从更多训练实例中受益。对于仅考虑结构信息的基于GNN 的模型，RDGCN 明显优于其他模型，这是因为RDGCN 模型考虑从邻域结构入手，缓解了结构异质性所带来的影响，体现出解决结构异质性的重要性。

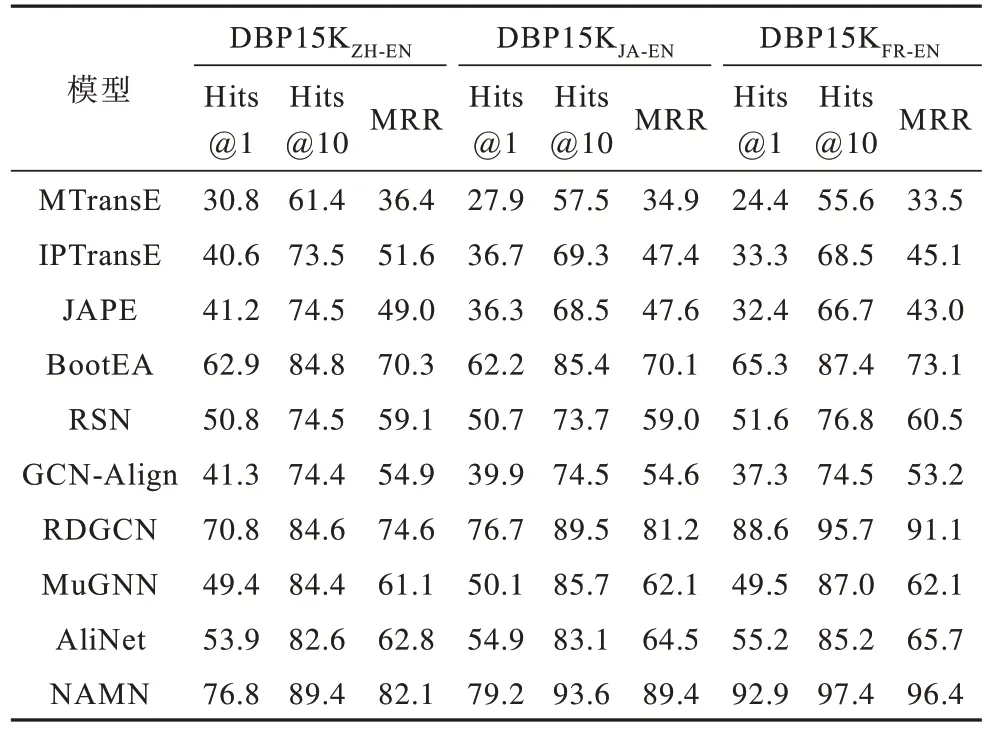
表4 不同实体对齐方法性能比较Table 4 Performance comparison of different entity alignment methods %

为进一步证明NAMN 模型的有效性，在DBP15K 的另外3 个数据集上进行对比实验。这3 个数据集分别是DBP15KEN-ZH（英语-中文），DBP15KEN-JA（英语-日语），DBP15KEN-FR（英语-法语），实体对齐的结果比对如表5 所示。可以看出，所有模型的性能都有所下降，但NAMN 模型明显优于另外3 个模型，NAMN 模型的Hits@1 的值要高于另外3 个模型约30%以上，其中，在DBP15KEN-FR数据集中Hits@1 达到了最高，充分证明了NAMN 模型的有效性和鲁棒性。

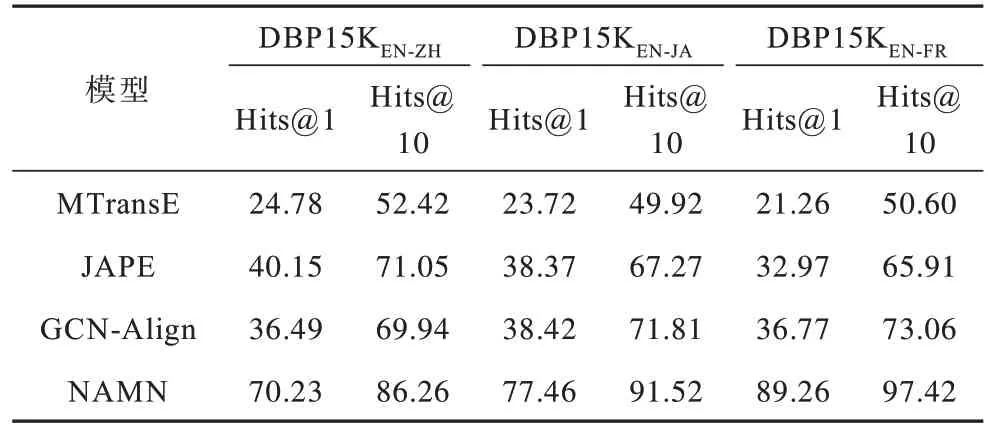
表5 实体对齐结果比较Table 5 Comparison of entity alignment results %

为更直观地表现NAMN 模型的性能，在DBP15K 数据集上，采用Hits@1 到Hits@50 以10 为步长的多个基准进行比较，选择JAPE、GCN-Align和AliNet 作为对比模型，具体如图3 所示，其中横坐标为Hits@K。可以看出：NAMN 模型的Hits@K值均高于其他模型，在DBP15KJA-EN和DBP15KFR-EN上都取得了最高的得分；AliNet 模型的Hits@K值在K取20 之后，得分接近NAMN 模型，说明缓解实体邻域结构的异质性有利于实体对齐，但AliNet 模型的Hits@1 明显低于NAMN 模型，说明NAMN 模型具有更好的对齐性能。

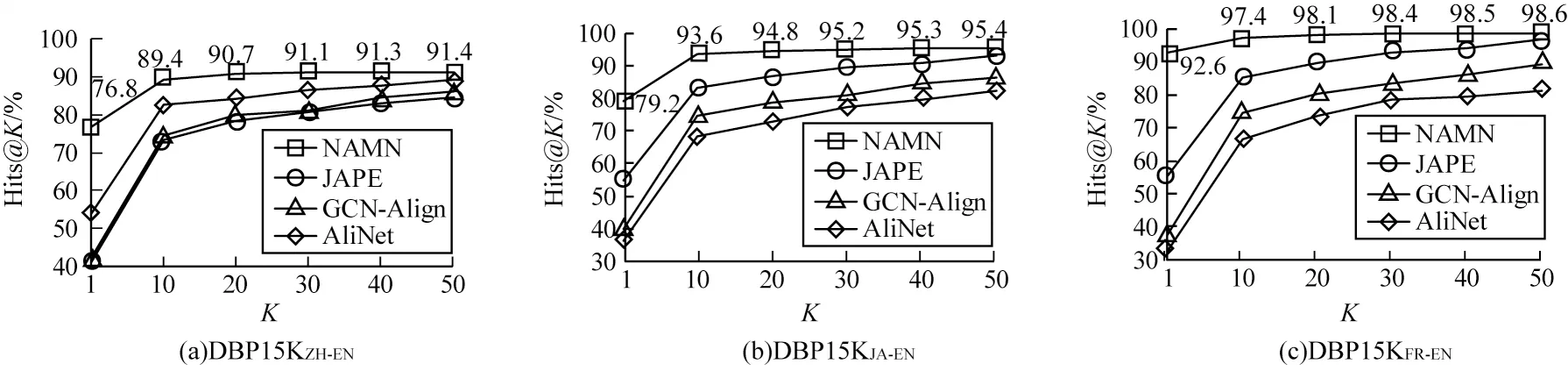
图3 DBP15K 数据集上Hits@K 得分结果比较Fig.3 Comparison of Hits@K score results on DBP15K dataset

3.4 结果分析

NAMN 模型使用门控机制和邻域采样策略来实现实体对齐，因此，分别对这两个策略进行分析。

将NAMN模型在DBP15K数据集上采用随机采样策略来进行比较，具体结果如图4所示。可以看出，NAMN模型可以提供更好的结果，本文的采样策略可以有效地选择信息量更大的邻居。对DBP15K数据集，两个模型均可达到性能平稳状态，当采样大小为3时，两个模型的性能更高。但随着采样大小的增大，性能会有所下降，说明较大的采样会引入更多的噪声。

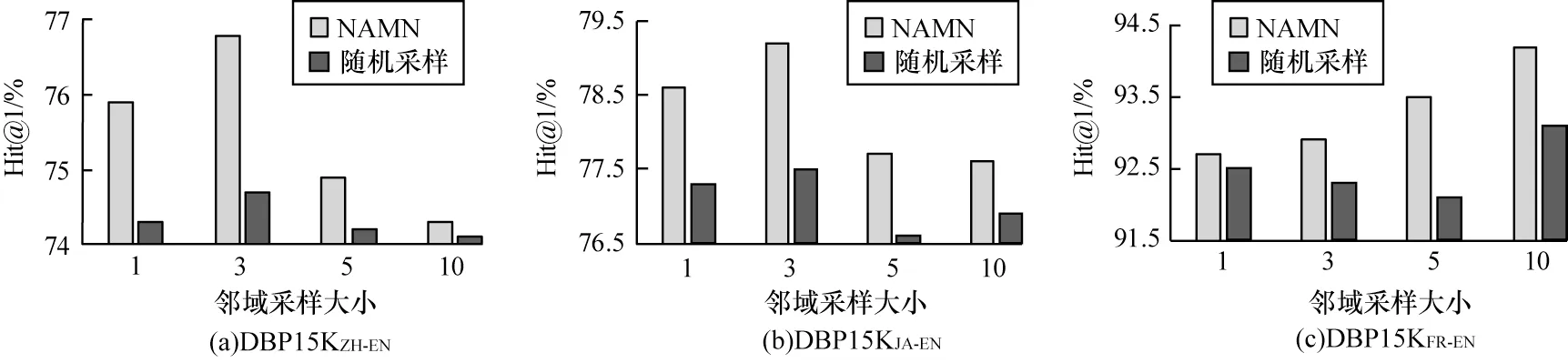
图4 DBP15K 数据集上邻域抽样策略与随机采样策略的结果比较Fig.4 Result comparison of neighborhood sampling strategy and random sampling strategy on DBP15K dataset

在聚合多跳邻居方面，本文使用不同的策略来设计NAMA 的不同变体。变体1（NAMN-1）将实体的一跳和二跳邻居平等对待，使用GNN 层直接聚合邻居信息；变体2（NAMN-2）用加法运算符替换门控机制；变体3（NAMN-3）用GAT 来替换本文所用的注意力机制。由表6 可以看出：NAMN-1 的实验结果很差，这表明使用GNN 层来直接聚合二跳邻居会引入很多的噪声信息，严重影响对齐性能；NAMN-2 的实验结果较差，这表明加法机制只是简单的将邻居信息结合，并不会像门控机制那样选择性地组合各个维度上的邻居信息表示；NAMN-3 的实验结果比NAMN 略差，这表明本文所用注意力机制能够优化对齐效果。因此，对于远距离邻居选择，门控机制和注意力机制至关重要。

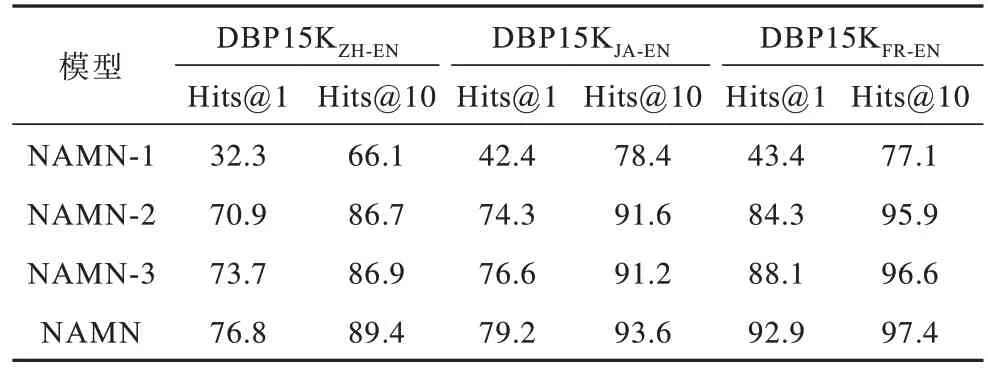
表6 NAMN 不同变体对齐结果比较Table 6 Comparison of alignment results of different variants of NAMN %

在DBP15K 数据集上1～4 层的AliNet 实验结果如图5 所示，其中横坐标为AliNet 的层数。可以看出：当AliNet 的层数为2 时，所有指标达到了最佳性能；当AliNet 具有更多层时，其性能也会下降。

图5 DBP15K 数据集上不同AliNet 层数的实验结果比较Fig.5 Experimental result comparison of different AliNet layers on DBP15K dataset

4 结束语

为提高实体对齐的准确性，本文提出邻域聚合匹配网络（NAMN）模型。从实体邻域角度出发，通过门控邻域聚合、邻域匹配和对齐预测3 个阶段判定实体是否对齐，解决知识图谱间普遍存在的结构异质性问题。实验结果表明，在DBP15K 数据集上，该模型的Hits@K指标达到75%以上。后续将利用实体的语义信息和关系的映射属性提高实体对齐的准确度，并进一步改进邻域的匹配策略，降低模型的复杂度，从而扩大模型的应用范围。