雷达辐射源信号分选识别特征性能评价的改进灰色关联模型
普运伟,吴海潇,姜 萤,余永鹏
(1.昆明理工大学信息工程与自动化学院,昆明 650500;2.昆明理工大学计算中心,昆明 650500)
引 言
雷达辐射源信号分选与识别是现代电子对抗的重要组成部分,它可截获敌方雷达参数进行分析,甄选出作战信息等关键因素,以便对战场进行势态评估和敌对风险分析,是对敌制胜的关键手段,对国防科技的发展具有重大意义。然而随着电磁环境的日趋复杂及分选识别技术的不断发展,如何对分选识别特征性能进行有效、合理的评估已成为这些特征投入战场应用的制约因素,这直接关系着电子侦察信号处理的效能改进。然而,国内外在设计合理且有效的综合评价模型上的研究仍然乏善可陈,例如:文献[1]提出了Logistic 回归模型对雷达辐射源信号进行特征评估,但只利用特征的正确识别率进行规划求解,并未提出完备的评价体系,评价结果有失偏颇;文献[2]引入雷达辐射源测试识别结果来进行模糊评判,但其模糊度由优、良等评语性等级设定,且采用层次分析法获取指标权值,整体评价框架不够客观;文献[3]采用层次分析法进行指标权重的确定,即将评价指标两两比较后根据重要程度进行权重赋值,缺乏一定的客观性;文献[4]只以参数间的距离作为评价度量,缺乏全面性;文献[5]虽从多指标角度构建了评价体系,但仅对雷达信号的熵特征进行评价,缺乏普遍适用性;文献[6]通过群体智能寻优来确定指标权重,仅从单一时间段进行分析,并未考虑到不同信噪比下信号参数的影响,评价结果不够准确。总体而言,传统的雷达辐射源信号分选识别特征评价方法多数存在评价指标单一、权重设定不合理等问题,这仅能从某些侧面反映分选识别特征性能,在复杂电磁环境中,既无法保证评估结果的科学性,也难以满足实际战场需求,并且多数方法仅对单时段(即静态)情况进行评价研究,然而实际决策中,诸多问题常需要融合不同时间段的测度信息进行探讨,因此通过动态层次分解来进行评价更具有实际意义。基于以上背景,本文提出了一种在区间直觉模糊数的形式下,基于多指标、多时段、多特征的角度将参数信息进行动态层次分解,以探索动态多指标评价模型建立的方法。
在雷达辐射源信号的分选识别过程评价中,考虑到特征参数不可避免地会受到噪声的影响,故而建立以不同信噪比为基础的动态层次分解模型;考虑到信号参数来源不够完备且受到多径效应影响,参数模型具有一定的模糊性,故在构建决策矩阵时,采取区间直觉模糊(Interval⁃valued intu⁃itionistic fuzzy,IVIF)思想[7]来反映参数信息;考虑到信号参数属于多维非线性数据,可采取改进灰色关联法对备选特征进行排序。为此,本文设计了一种结合区间直觉模糊思想和改进灰色关联法的雷达辐射源信号分选识别特征评价方法。该方法在动态信噪比层次下构建评价矩阵,进一步通过公式集结为区间直觉模糊数型的综合决策矩阵;然后建立基于多特征离差最大化的优化模型,确定指标属性;进而构建改进灰色关联评价体系求得特征方案的排序结果;最后通过实验分析验证本文模型的有效性和良好性能。区间直觉模糊和灰色关联法是根据数据信息量来进行分析的评价算法。该方法将初始数据进行模糊处理,能够有效避免因数据来源限制、背景因素等造成的信息损失。此类算法对数据没有服从线性条件的前提要求,适用于高维非线性拟合和非高斯数据的群体评价,在系统制造[8]、项目投资[9]及社交网络[10]等领域均有广泛应用。经前期研究已证明雷达辐射源信号分选识别属于多维非线性数据[6],因此灰色关联法非常适合用来研究雷达辐射源信号分选识别特征评价问题。
1 分选识别特征评价指标体系
本文通过建立一个系统性的分层聚合模型来评价雷达辐射源信号的分选识别性能,为遴选最佳特征提供全面而合理的决策支撑。考虑到特征提取的复杂性、特征提取方法的鲁棒性和所提取特征的分离能力,本文主要从3 个方面设定了6 个评价指标来反映雷达辐射源信号分选识别特征性能,构建如图1 所示的评价指标体系。图1 中,分选准确率C31为效益型指标,其余5 个指标为成本型指标。时间复杂性C11以各信噪比下进行n次特征提取实验所耗费的平均时间来度量,以区间数[aL,aU]表示;考虑到运算过程中实际问题的规模,需要对提取特征的计算量进行分析,故采取算法复杂度C12对各特征方案的算法阶数进行量化,具体评价依据可参考文献[3];噪声适应度C21反映特征参数在不同噪声下的适应情况,即在同一噪声水平下提取到各信号样本的无偏标准差,以区间数[bL,bU]表示;为描述各特征参数的抗噪性能,即特征在不同信噪比下的跃迁情况,可采用噪声稳定性C22进行计算,将相邻信噪比范围内所有调制信号分选识别后的样本数据进行差值计算,结果以区间数[cL,cU]表示;分选准确率C31以区间数[eL,eU]表示,即各固定信噪比下的所有调制信号的平均分选成功率;类间离散度C32用来衡量特征参数的聚类效果,为同一信噪比下各类调制信号聚集率的最大差值,以区间数[gL,gU]表示。

图1 雷达辐射源信号分选识别特征综合评价指标体系Fig.1 Comprehensive evaluation attribute sys⁃tem of radar emitter signal sorting and identification features
2 基于区间直觉模糊思想的改进灰色关联评价模型
2.1 动态层次分解的区间直觉模糊矩阵
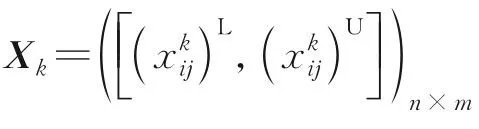

类似地,对成本型评价指标的标准化处理为

依据文献[12]可得矩阵Yk转换为区间直觉模糊数的过程如下:
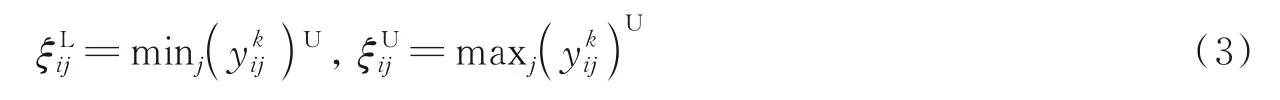
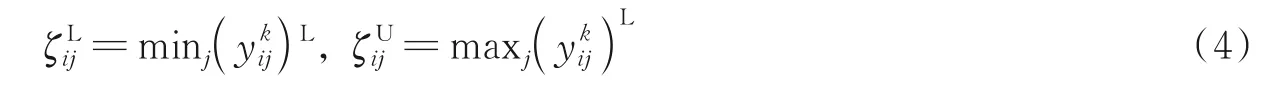


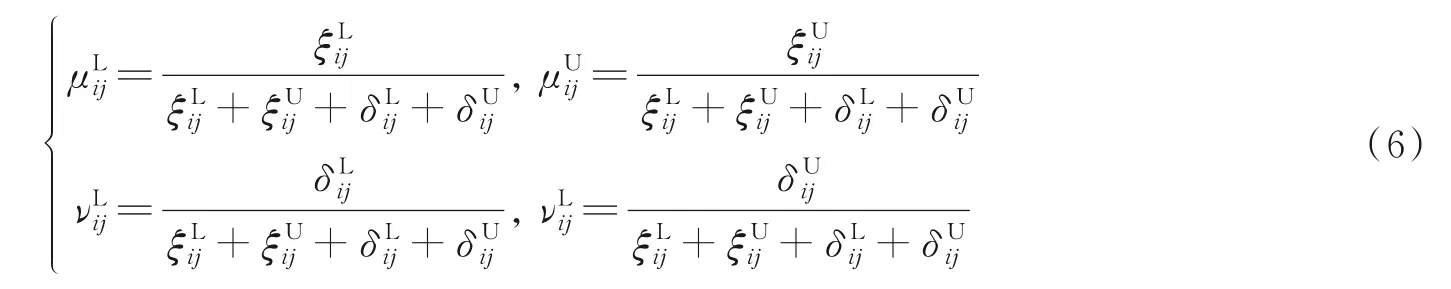
(4)集结单一区间直觉模糊数可得到综合决策矩阵为R=(rij)n×m。
2.2 改进灰色关联评价模型
逼近理想点法(Technique for order preference by similarity to ideal solution,TOPSIS)和灰色关联法是2 种典型的应用于多维数据处理的评价方法。TOPSIS 是以评价对象与正负理想方案之间的距离作为评价依据,但这仅能反映两者之间的位置关系,不能全面地反映某一评价对象的指标在整个体系中的重要程度,且此方法并未考虑到权重的影响,故无法保证结果的准确性。传统的灰色关联法同样以评价对象与理想对象的距离测度来进行衡量,但仅考虑了最佳偏好结果,并未考虑到不同备选方案相对于最差理想方案的测度信息。因此本文将TOPSIS 的评价依据引入到灰色关联法中,设计一种改进灰色关联评价模型,从而得到更稳定的评价效果,步骤如下:
步骤1确定在综合决策矩阵R中第i个特征在第j个指标下的正理想解fj+及理想解fj-[13]

步骤2确定各特征在不同指标下与正、负理想方案的关联系数分别为[13]
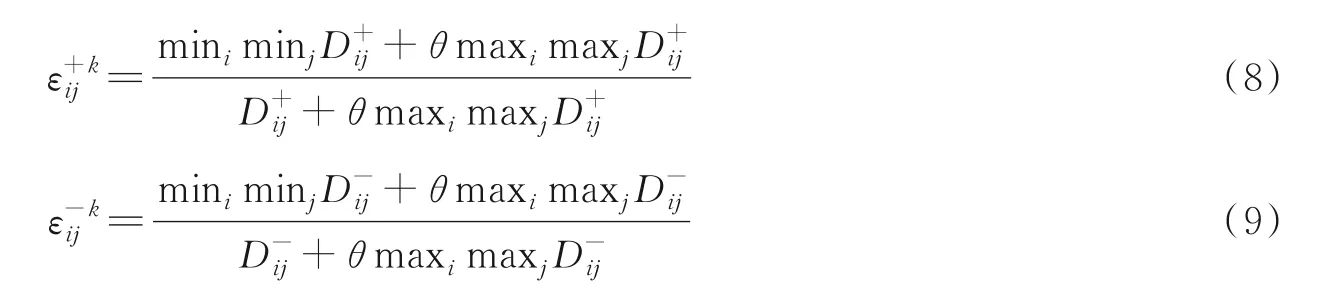


步骤3通过建立以在所有指标下特征Ai和其他特征Ak间总离差最大化为目标的数学规划模型来确定各属性权重,即求解如下优化模型
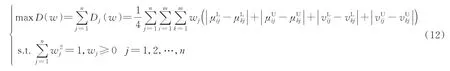
式中Dj(w)表示对指标Cj而言,所有特征方案和其他特征方案的总离差,表达式为

为求解式(13),可构造Lagrange 函数并求其偏导数,经过归一化处理后可得指标权重为

步骤4将由式(14)得到属性权重及式(8,9)得到的关联系数代入到式(15,16)中,计算出每个方案在所有指标下正、负灰色关联度为[14]

步骤5结合TOPSIS 的思想,将TOPSIS 中各特征方案与正、负理想解的距离测度转换为灰色关联度,得到综合评价值为[14]

式中:ρ为决策系数,ρ=0.5。对于模型整体,γi越大,则被评价特征距离正理想解最近,而距离负理想解最远,因此特征性能越优;反之γi越小则特征性能越差。
3 实验分析
为验证所提特征评价模型的可行性及有效性,选取雷达辐射源信号的模糊函数主脊(Ambiguity function main ridge,AFMR)切面特征A1[15]、模糊函数(Ambiguity function,AF)等高线特征A2[16]、小波脊频级联特征A3[17]共3 种典型特征提取方案来进行评价和敏感性分析,并与灰色关联法分析的结果进行对比。
3.1 特征评价结果与分析
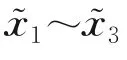
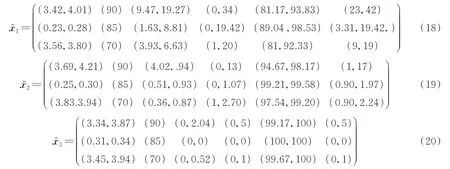
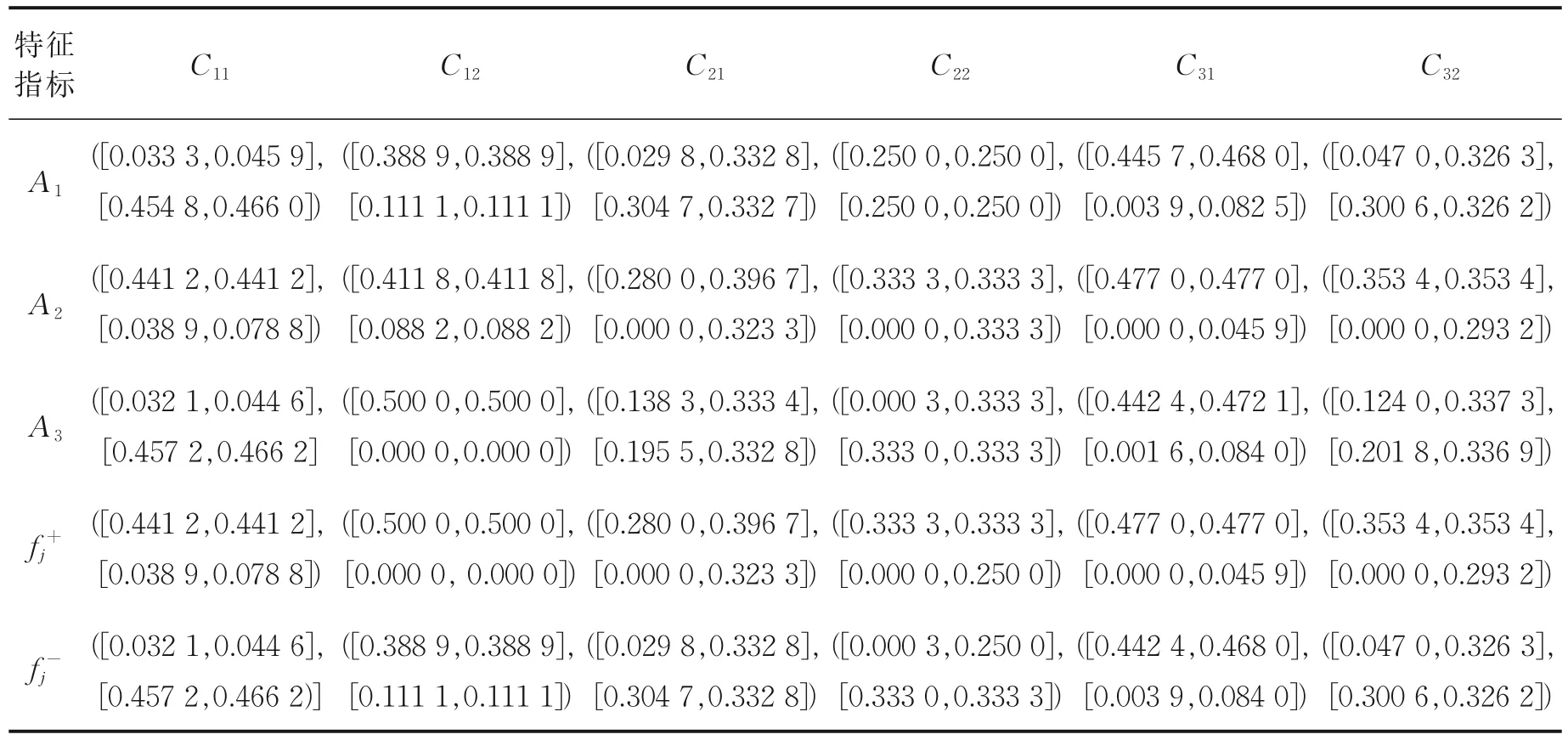
表1 区间直觉模糊综合决策矩阵Table 1 Interval intuitionistic fuzzy comprehensive decision matrix

表2 正理想解系数Table 2 Positive ideal solution coefficient

表3 负理想解系数Table 3 Negative ideal solution coefficient
依据1.2节步骤3中的模型求解出指标权重为ω=(0.376 5,0.103 8,0.146 8,0.194 5,0.020 0,0.158 4)。依据式(15,16)求出各特征在所有指标下正灰色关联度为:γ+k=0.476 1,0.935 1,0.516 2,负灰色关联度为:=0.902 1,0.901 8,0.902 1。
依据式(17),结合TOPSIS 法的思想,将TOPSIS 法中各特征与正、负理想解的距离测度转换为灰色关联度,得到综合评价值为:γ1=0.345 5,γ2=0.509 1,γ3=0.364 0,故各特征方案排序结果为A2>A3>A1。
3.2 敏感度分析
为了预测此评价模型的风险性,可采取摄动法对评价指标的系数和权重进行敏感性分析,通过权重和系数在特定范围内的微小变动对评价信息造成的干扰来观察各特征方案排序的相应变化。
3.2.1 系数敏感度分析
在式(17)中,评价系数从均衡策略考虑取值ρ=0.5。为验证结果的敏感性,在ρ=[0,1]中以步长0.1 进行取值,分析综合评价值γi随决策系数ρ变化后的性能。综合评价值随决策系数变化的敏感度分析如图2 所示。由图2 可知,在进行的9 次实验中,不论ρ如何变化,特征方案排序结果均保持一致,仍为A2>A3>A1,通过计算得出系数敏感性实验稳定性结果达到100%,验证了本实验的有效性和可行性。
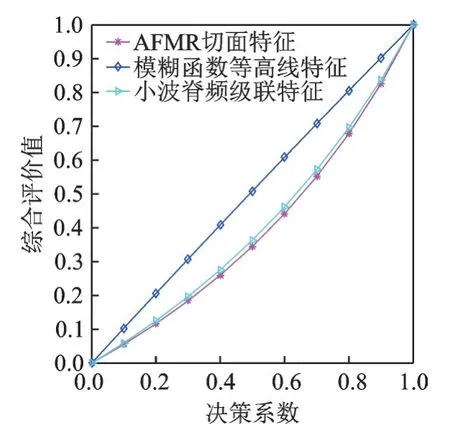
图2 综合评价值随决策系数变化的敏感度分析Fig.2 Sensitivity analysis of comprehen⁃sive evaluation value changing with decision coefficient
3.2.2 权重敏感度分析

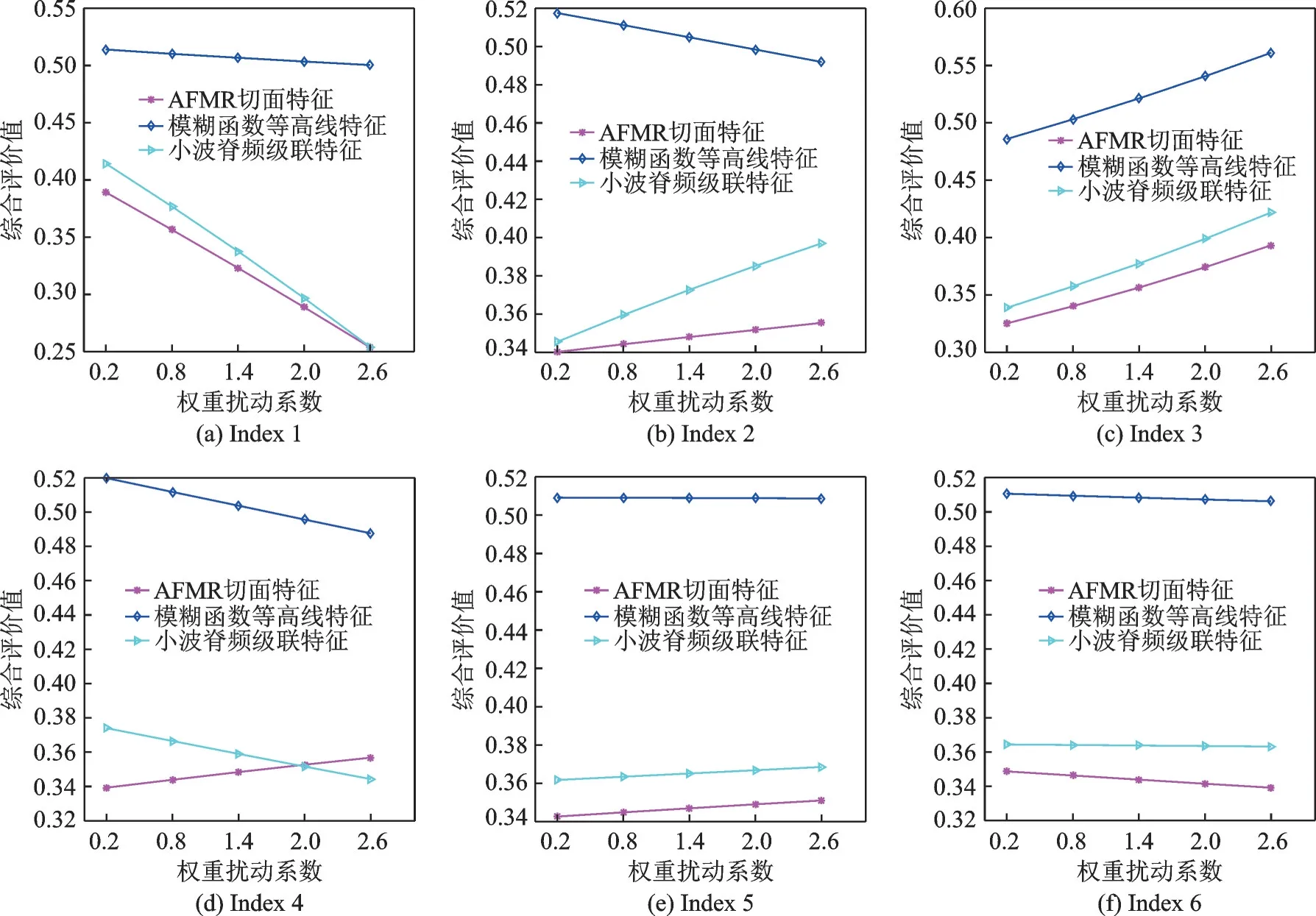
图3 综合评价值随权重变化的敏感度分析Fig.3 Sensitivity analysis of comprehensive evaluation value changing with weight
3.3 对比实验分析
3.3.1 灰色关联法对比分析
采取未改进的灰色关联法对综合决策矩阵R进行分析计算[19],并将此方法与所提方法进行对比。考虑所有特征方案在动态层次模型下获得完全肯定情况,即将特征方案的理想解均设定为([1,1],[0,0])。依据Euclidean 距离计算出各特征方案的评价信息相对于理想解的距离,构成距离矩阵为

在指标Cj的条件下,结合式(21)计算特征方案相对于理想解的接近程度,以灰色关联系数来表示,表达式为
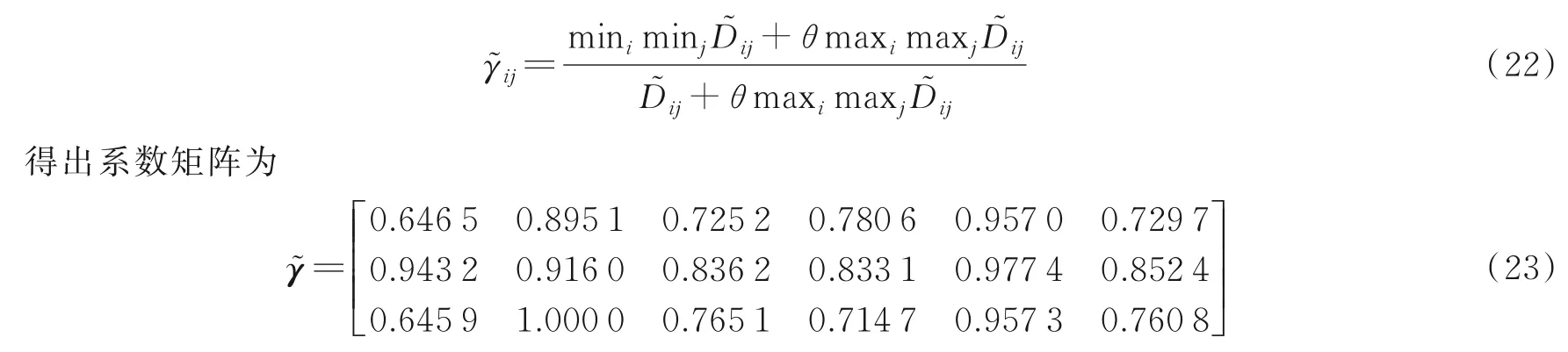
将本文已求得的指标权重并结合式(23)代入式(24),计算各特征方案在所有指标下的综合灰色关联系数并进行排序越大,排序越靠前,特征性能越佳。

利用3.2 节的权重敏感度分析方法,对灰色关联法得到的评价结果进行分析,同样对于各评价指标权重wj,当取不同参数φ时得到相应的特征性能排序。本次对比实验干扰参数取值与所提实验方法一致,共进行30 次实验,发生排序结果变化的为指标1、指标2 及指标4,图4 示例性地给出部分指标下灰色关联法权重敏感度分析。

图4 灰色关联法权重敏感度分析Fig.4 Analysis of weight sensitivity of grey correlation method
由图4 可知,在30 次实验中,A2一直为最优特征,A1与A3发生4 次排序变化,本实验的稳定性为86.67%,与所提方法相比,前者对权重改变更为敏感,不稳定性也更高。
3.3.2 得分函数法对比分析
依据文献[20]采取的得分函数法对综合决策矩阵R进行分析计算,并将此方法与所提方法进行对比。
首先,由区间直觉模糊加权平均算子(Interval⁃valued intuitionistic fuzzy weighted average,IVIF⁃WA)集成综合决策矩阵R中第i行所有特征的模糊值,结果依次为:=([0.133 8,0.228 5],[0.280 8,0.309 1])=([0.383 3,0.399 1],[0,0.158 2]),=([0.129 6,0.263 2],[0,0])。
其次,将各特征的模糊值代入式(25)中,计算出特征方案的得分值s(αi),并对特性性能依次排序[20]。设=([a,b],[c,d])为一个区间直觉模糊数,则称为的得分值,其中s为的得分函数,

依据式(25)所示的得分函数可知,各特征性能排序为A2>A3>A1。此方法的排序结果与本文提出的改进灰色关联法得到的结果一致,证明了所提方法的有效性和良好性能。但因其未考虑到指标权重的影响,且不同区间直觉模糊数的得分函数可能会相同,进而影响评价结果。故从多数据样本的角度看,采用改进灰色关联法得到的结果更为合理。
综合以上实验可知,改进灰色关联法结合了TOPSIS 的思想,既考虑了不同指标下的权重,也兼顾了评价特征与最优及最劣解之间距离的均衡性,得到的可行解在理论实验、实际环境及敏感性分析中均表现出较为可靠的评价结果,证明了所提方法的有效性和良好性能。
4 结束语
在对雷达辐射源信号分选识别特征的研究中,构建有效的特征综合评价机制是一项具有实际意义的研究。为此,本文创新性地将雷达辐射源信号参数特征转换为区间直觉模糊评价问题,同时在模糊情形下建立区间数型的评价指标体系,并将引入不同信噪比作为分析维度,提出一种基于改进灰色关联的雷达辐射源信号特征评价模型与方法。该方法采用区间模糊的思想构建动态层次分解的评价矩阵,有效提高了评估精度;然后融合不同层次下的评价信息,实现群决策矩阵的集成,使其更具有现实意义;进而采取离差最大化求解群矩阵中各指标权值;最后基于改进的灰色关联法对方案进行评估,使得评估结果更为准确和客观。仿真实验与对比分析结果表明,该方法能够对所提取的特征进行相对合理的评价,为雷达辐射源信号分选识别特征评价研究提供切实可行的研究思路,对电子对抗中信号特征提取与性能分析具有一定的指导意义。下一步,将进一步完善综合特征评价指标体系并优化评价流程,以便更加科学、客观及合理地对雷达辐射源信号分选识别特征进行综合评价。

