基于全空间误差补偿的钻孔轨迹测量系统的研究

李 渊， 燕 斌

(中煤科工集团西安研究院有限公司，陕西 西安 710077)

0 引言

保障煤矿安全生产是一切煤矿工作的前提，其中瓦斯事故是其主要的致灾因素之一。钻孔轨迹测量系统是支撑瓦斯治理的有力武器，它可以有效测量瓦斯抽放孔的实际钻进轨迹，对于评价瓦斯抽采效果具有重要的支撑作用，因此可以说它是保障矿工安全生产的重要设备，是抵挡煤矿灾害的“定海神针”。

通常煤矿井下瓦斯抽采孔的钻孔尺寸有限，钻孔直径为Φ73 mm，因此虽然基于光纤陀螺的惯性导航技术的精度较高，但由于其尺寸较大导致不适用于煤矿井下钻孔轨迹测量，因此目前煤矿井下应用的轨迹测量系统大多是基于磁性传感器的姿态测量技术。基于磁性传感器的姿态测量技术依靠测量地球磁场和重力场实现钻孔倾角和方位角测量，虽然精度较基于光纤陀螺的惯性导航技术稍差，但由于其体积较小，功耗较低，因此普遍应用于煤矿井下轨迹测量领域[1-7]。

由于钻孔轨迹测量系统存在诸如安装结构、传感器误差以及周围测量环境磁场因素的影响，会导致测量地球磁场和重力场出现偏差，进而导致钻孔轨迹测量结果出现误差，严重影响测量系统的测量精度，因此需要对系统中存在的传感器制造误差、机械安装误差以及环境误差进行校正。基于上述目的，该文将分析基于磁性传感器的煤矿井下轨迹测量系统中的测量原理，研制基于PNI磁传感器和MEMS加速度计的钻孔轨迹测量系统，经过详细分析系统误差来源，建立高精度、全空间误差补偿模型对系统中的各种误差进行修正，进而提高钻孔轨迹测量的精度，为精准实现瓦斯抽采提供可靠的技术支撑。

1 测量原理

测量钻孔倾角和方位角是钻孔轨迹测量系统的最终目的，基于磁性传感器的姿态测量技术为了达到该目的通常需要通过三维正交的磁性传感器来感知地磁场分量，通过三维正交的加速度传感器来感知地球重力场分量，然后通过相关计算实现钻孔倾角和方位角测量，其简易结构示意图如图1所示。

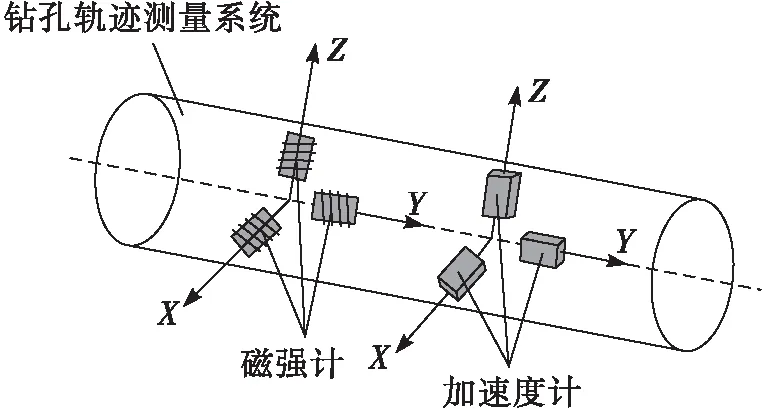
图1 钻孔轨迹测量系统简易结构示意图

钻孔倾角的计算表达式如下：

(1)

式中：Gx代表仪器坐标系中地球重力场在X轴方向的分量；Gy代表仪器坐标系中地球重力场在Y轴方向的分量；Gz代表仪器坐标系中地球重力场在Z轴方向的分量；G0代表地理坐标系中地球重力场在Z轴方向的分量。

钻孔方位角的计算表达式如下：

(2)

式中：Bx代表仪器坐标系中地球磁力场在X轴方向的分量；By代表仪器坐标系中地球磁力场在Y轴方向的分量；Bz代表仪器坐标系中地球磁力场在Z轴方向的分量。

2 硬件设计

根据测量原理可知，为了求解钻孔倾角和方位角需要通过磁性传感器和加速度传感器，因此该文设计了基于PNI磁传感器和MEMS加速度计的钻孔轨迹测量系统硬件方案，主要包括测量探管和防爆手机两部分，其中测量探管完成钻孔倾角和方位角测量功能，防爆手机完成人机交互和数据显示功能，总体方案如图2所示。

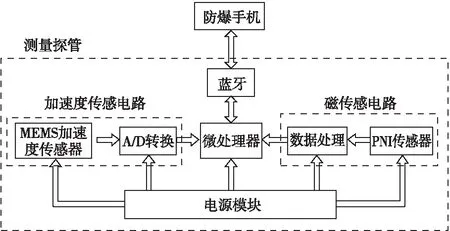
图2 钻孔轨迹测量系统总体方案

测量探管主要包括数据采集、数据处理以及数据传输三个部分，其中数据采集包括使用MEMS加速度传感器测量地球重力场三个分量，以及使用PNI磁性传感器测量地球磁场三个分量[8-10]；数据处理是利用微处理器对采集的三轴加速度值和三分量地磁信息进行解算，进而通过式(1)和式(2)分别计算出此刻钻孔对应的倾角和方位角；数据传输是微处理器通过蓝牙接口将解算的倾角和方位角按照规定的协议无线输出至防爆手机[11-14]。

为了获取地球重力场信息，该文采用了KXR94三轴MEMS加速度计。该芯片芯能优越，零加速度漂移仅为±150 mg，±2 g的测量范围满足测量需求，并且非线性度仅为0.1%，正常工作温度范围为-40 ℃至85 ℃。此外，该芯片功耗较低，驱动电压范围为2.8～3.3 V，工作电流仅为1.03 mA。KXR94芯片输出信号为电压值，为了将此信号采集至微处理器，需要设计相应的A/D采集方案。该文采用了凌特16位A/D转换器LTC1865L实现模拟信号数字化，由于加速度信息为三路，而LTC1865L为双通道采集，因此该文采用了2片LTC1865L实现加速度信息采集。该文设计的加速度传感电路的电气原理图如图3所示。

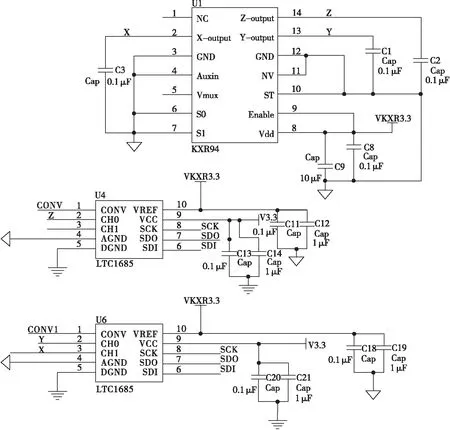
图3 加速度传感电路的电气原理图

为了获取地球磁场信息，该文采用了美国PNI公司生产的SEN-R65/Z65磁传感器和PNI12927驱动模块，其中2个SEN-R65磁传感器用于感知X轴和Y轴，SEN-Z65磁传感器用于感知Z轴。SEN-R65/Z65磁传感器采用螺旋管缠绕高磁导率磁芯结构，与外部电阻形成LR振荡电路，通过对比和计算正向电压和负向电压时相同数量的波形周期时间得到外部的磁场强度。该芯片的分辨率高达10 nT，并且功耗较低，在8 Hz采样率时功耗低至1.5 mW左右，满足磁场测量需求。该文设计的PNI磁传感电路电气原理图如图4所示。

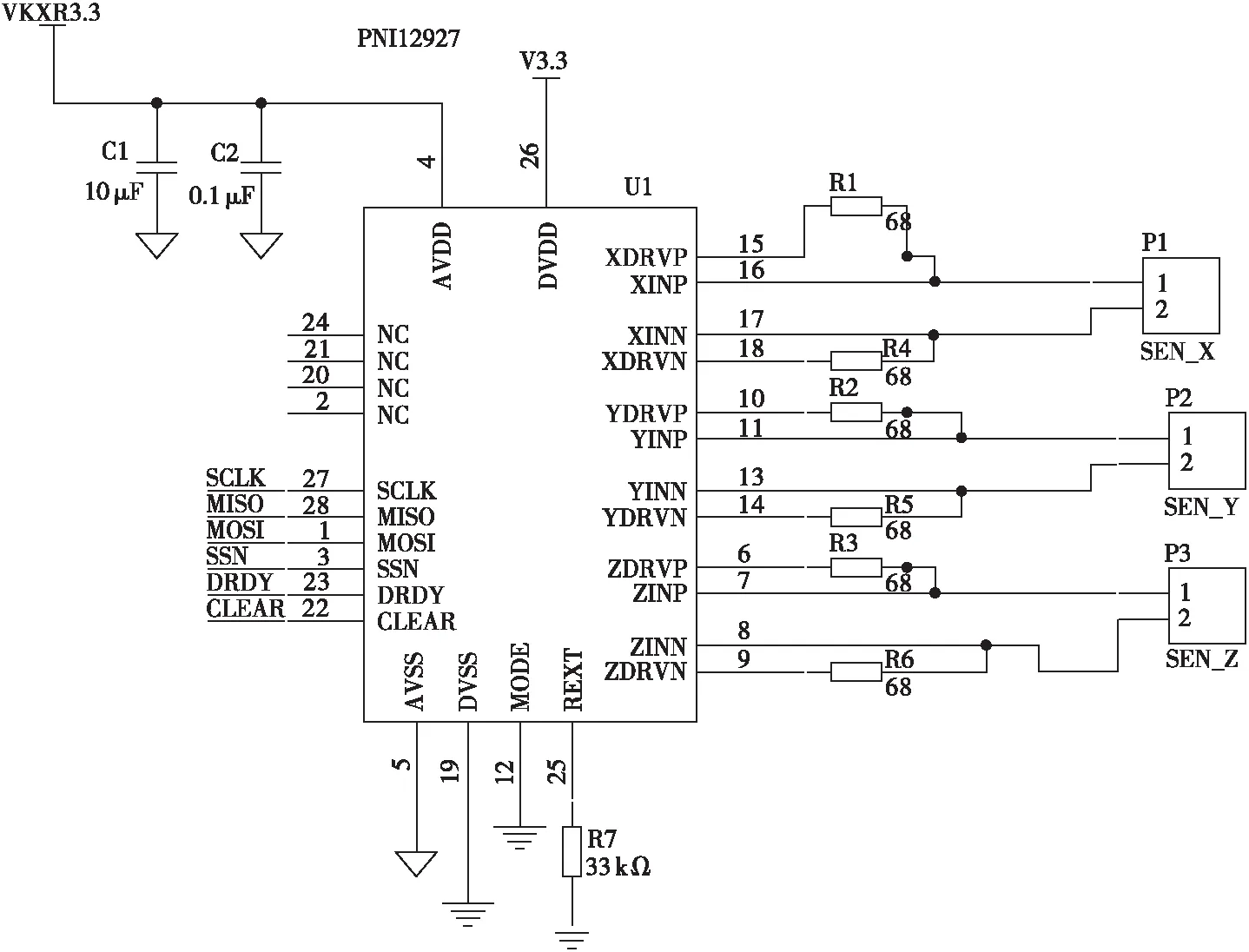
图4 磁传感电路的电气原理图

此外，由于测量探管需要随钻测量，最高承受水压不超过20 MPa，并且考虑探管材质不能带来磁性干扰，因此该文采用了铍铜进行探管外壳加工。为了完成数据显示和人工交互，该文采用了市场成熟的防爆手机。该文设计的钻孔轨迹测量系统如图5所示。

图5 钻孔轨迹测量系统实物照片

3 误差分析

根据误差的特点和性质，经过分析后该文设计的钻孔轨迹测量系统的误差由随机误差和系统误差构成[15-17]。

(1)随机误差是钻孔轨迹测量系统在使用过程中因为一系列有关因素的微小随机波动进而造成的测量误差，无明显变化规律，具有相互抵偿性，影响较小。

(2)系统误差是钻孔轨迹测量系统本身存在的误差，通常由很多因素造成，主要分为传感器制造误差、传感器安装误差以及应用环境误差三大类[18-20]。

传感器制造误差是传感器芯片在生产制造过程中形成的固有误差，主要包括零位误差、灵敏度误差以及正交误差，其中零位误差产生主要是由于传感器测量电路和A/D转换电路中不可避免存在的零点残余电压或零点漂移。灵敏度误差是由于传感器在三轴方向上灵敏度存在差异引起的测量误差，正交误差是指传感器的三个敏感轴之间存在不正交现象所引起的测量误差。

由于传感器在进行系统安装时会出现由于壳体存在机械加工误差导致传感器的三个敏感轴与整个系统的仪器坐标系三个坐标轴之间存在不重合现象，或者由于人为安装因素导致传感器的三个敏感轴与整个系统的仪器坐标系三个坐标轴之间存在不重合现象，进而产生传感器安装误差。该种误差是造成轨迹测量系统测量误差的主要因素。

环境误差是指当周围环境磁场存在干扰时，会对钻孔轨迹测量系统的磁性传感器产生影响，进而会使得方位角的测量产生误差。该种误差可以通过在使用过程中避开铁磁干扰实现消除。

综上所述，安装误差是造成轨迹测量系统测量误差的主要因素。为了提高钻孔轨迹测量系统的测量精度，该文将通过建立两种不同的误差模型对系统误差进行补偿。

4 误差补偿

根据该文对钻孔轨迹测量系统的误差分析可知，为了实现钻孔轨迹的高精度测量，必须对系统误差进行有效修正。针对这类误差，该文分别建立了三阶正交矩阵配合零偏系数以及三阶正交矩阵配合高次多项式的修正模型实现误差校正，其中三阶正交矩阵配合零偏系数的修正模型包括加速度修正模型和磁传感器修正模型。

加速度传感器的修正模型表达式如下：

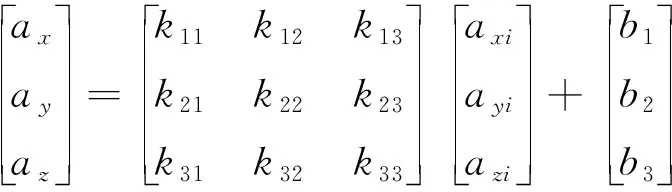
(3)

式中：ax为加速度传感器在X轴方向上的实际测量值；ay为加速度传感器在Y轴方向上的实际测量值；az为为加速度传感器在Z轴方向上的实际测量值，单位均为g；b1，b2，b3分别为加速度传感器的零偏，单位为g；axi为加速度传感器在X轴方向上的理论值值；ayi为加速度传感器在Y轴方向上的理论值值；azi为为加速度传感器在Z轴方向上的理论值；k12，k21，k31，k13，k23，k32为加速度传感器的正交误差系数；k11，k22，k33为加速度传感器的灵敏度误差。

磁传感器修正模型表达式如下：

(4)

式中：Hx0，Hy0，Hz0为磁性传感器的实际测量值(Gs)；t1，t2，t3分别代表磁性传感器零偏误差与硬磁材料测量误差在X轴方向、Y轴方向和Z轴方向的各自分量(Gs)；M矩阵为灵敏度误差、正交误差以及安装误差引起的综合误差。

由于传感器零位误差具有非线性特点，为了更好的补偿系统误差中的传感器零位误差和灵敏度误差，该文提出了采用高次多项式数值表达式对其进行高精度补偿，三阶正交矩阵配合高次多项式的加速度传感器修正模型表达式如下：

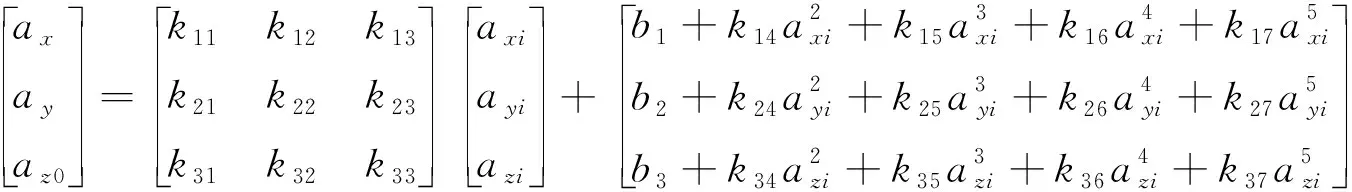
(5)

式中：kx4，kx5，kx6，kx7(x=1，…，3)为一到五次方有关的误差系数。

三阶正交矩阵配合高次多项式的磁传感器修正模型表达式如下：

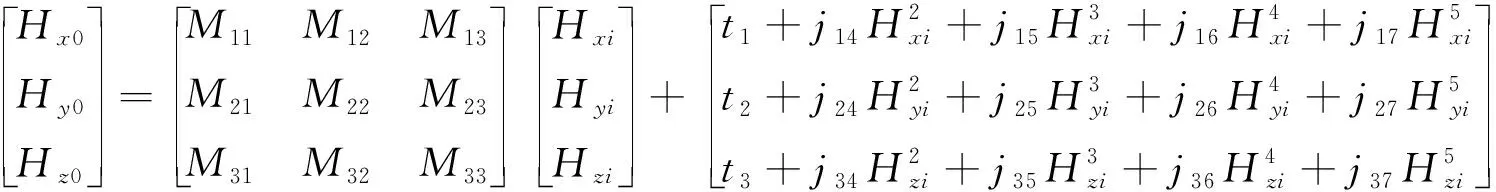
(6)

式中：jx4，jx5，jx6，jx7(x=1，…，3)为一到五次方有关的误差系数。

5 补偿测试

三阶正交矩阵配合零偏系数的修正模型包含24个系数，由于单一位置可提供三个方程组，因此为了求解公式(3)和公式(4)中的24个系数，理论上至少需要采集8个位置的数据进行求解。三阶正交矩阵配合高次多项式的修正模型包含48个系数，由于单一位置可提供三个方程组，因此为了求解公式(5)和公式(6)中的48个系数，理论上至少需要采集16个位置的数据进行求解。

为了测试误差补偿算法的实际应用效果，该文将从不同模型和不同点数两个方面进行测试。测试装置为大连华天精密仪器有限公司生产的TX-3S测斜仪调校装置，其三轴姿态角测量精度为≤±0.05°，三轴正交度为≤0.1°，三轴相交度为≤1 mm，完全满足钻孔轨迹测量系统的测试需求，测试装置如图6所示。

图6 TX-3S测斜仪调校装置

5.1 不同模型测试

该文针对三阶正交矩阵配合零偏系数的修正模型和三阶正交矩阵配合高次多项式的修正模型分别进行了测试，求解前者至少需要采集8个位置传感器数据，求解后者至少需要采集16个位置传感器数据。为了确保模型求解的合理性，该文在全空间均匀选取36个标定位置并利用最小二乘法拟合的原理求解误差模型的超定方程组。采集36位置时传感器相对应数据，通过公式(3)和公式(4)计算三阶正交矩阵配合零偏系数修正模型的误差修正系数，通过公式(5)和公式(6)计算三阶正交矩阵配合高次多项式修正模型的误差修正系数，然后通过求解公式(1)可计算得到钻孔倾角，通过求解公式(2)可计算得到钻孔方位角。

图7给出了36位置时采用两种误差模型求解倾角在不同角度时的误差对比。经过对比可知，采用三阶正交矩阵配合高次多项式修正模型的测量精度要显著高于三阶正交矩阵配合零偏系数修正模型的测量精度。

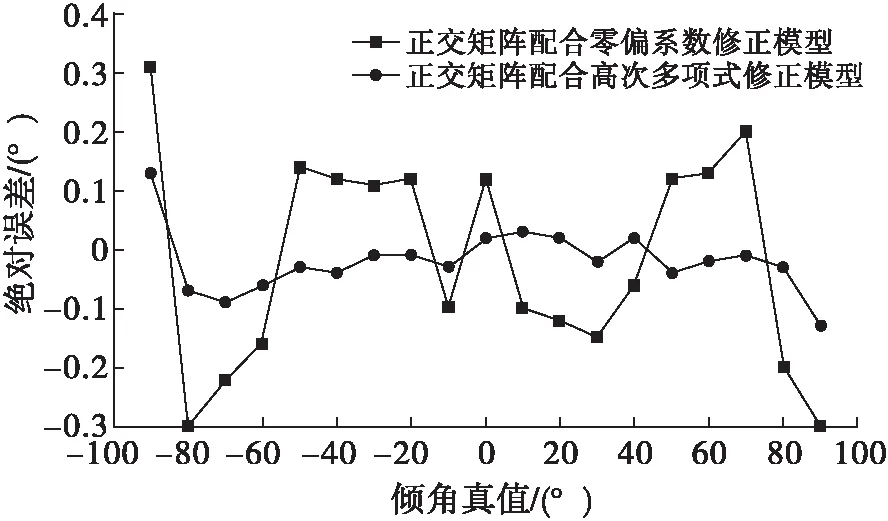
图7 两种误差模型求解倾角的误差对比

图8给出了36位置时采用两种误差模型求解方位角在不同角度时的误差对比。经过对比可知，采用三阶正交矩阵配合高次多项式修正模型的测量精度要显著高于三阶正交矩阵配合零偏系数修正模型的测量精度。

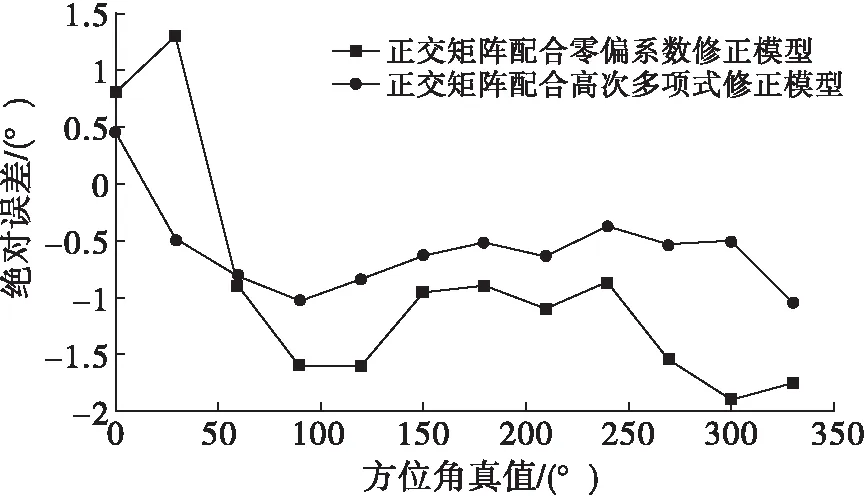
图8 两种误差模型求解方位角的误差对比

5.2 不同点数测试

该文在全空间范围内均匀选取不同数量的位置进行数据采集，用以解算两种模型中的修正系数，分别包括36、48和144标定位置。图9给出了均匀分布于全空间的36、48、144标定位置时倾角的测量结果，经过分析可以得出如下结论：小角度情况下，倾角采用36、48、144标定位置的测量精度变化不大；当倾角值较大时，虽然标定位置增加会提高测量精度，但是144标定位置相较于48标定位置的测量精度并没有发生显著提高，并且0.2°以内的倾角测量误差完全满足煤矿轨迹测量要求。

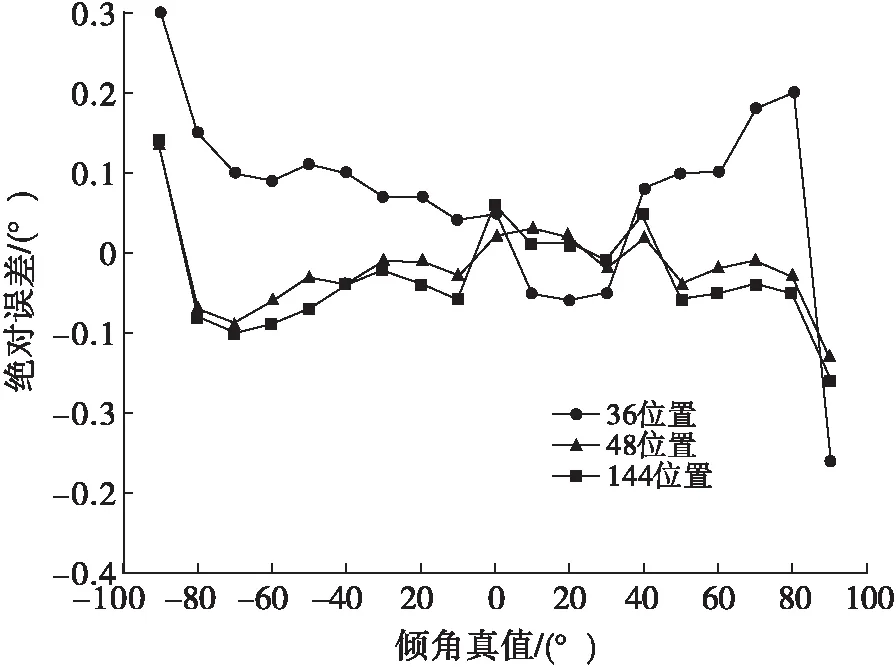
图9 不同位置点数时倾角的测量结果

图10给出了均匀分布于全空间的36、48、144标定位置时方位角的测量结果，经过分析可以得出如下结论：在0°～360°全范围内，随着标定位置增加方位角的测量误差减小，但标定位置数增大到48之后，精度并没有随着标定位置数的增加而显著提高，并且该点数位置下方位角误差能够控制在1.5°以内，完全满足煤矿测量要求。

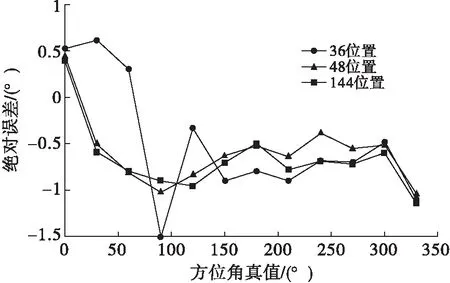
图10 不同位置点数时方位角的测量结果

6 井下试验

为了验证该文研制的钻孔轨迹测量系统的实际工作性能，2021年5月该仪器在晋能集团长治三元公司某矿进行了现场工业性试验，对钻场的探放水钻孔进行了钻孔轨迹测量。试验时实际钻进20米，每次间隔1米进行测量，测量数据如表1所示，钻孔轨迹三维空间示意图如图12所示。

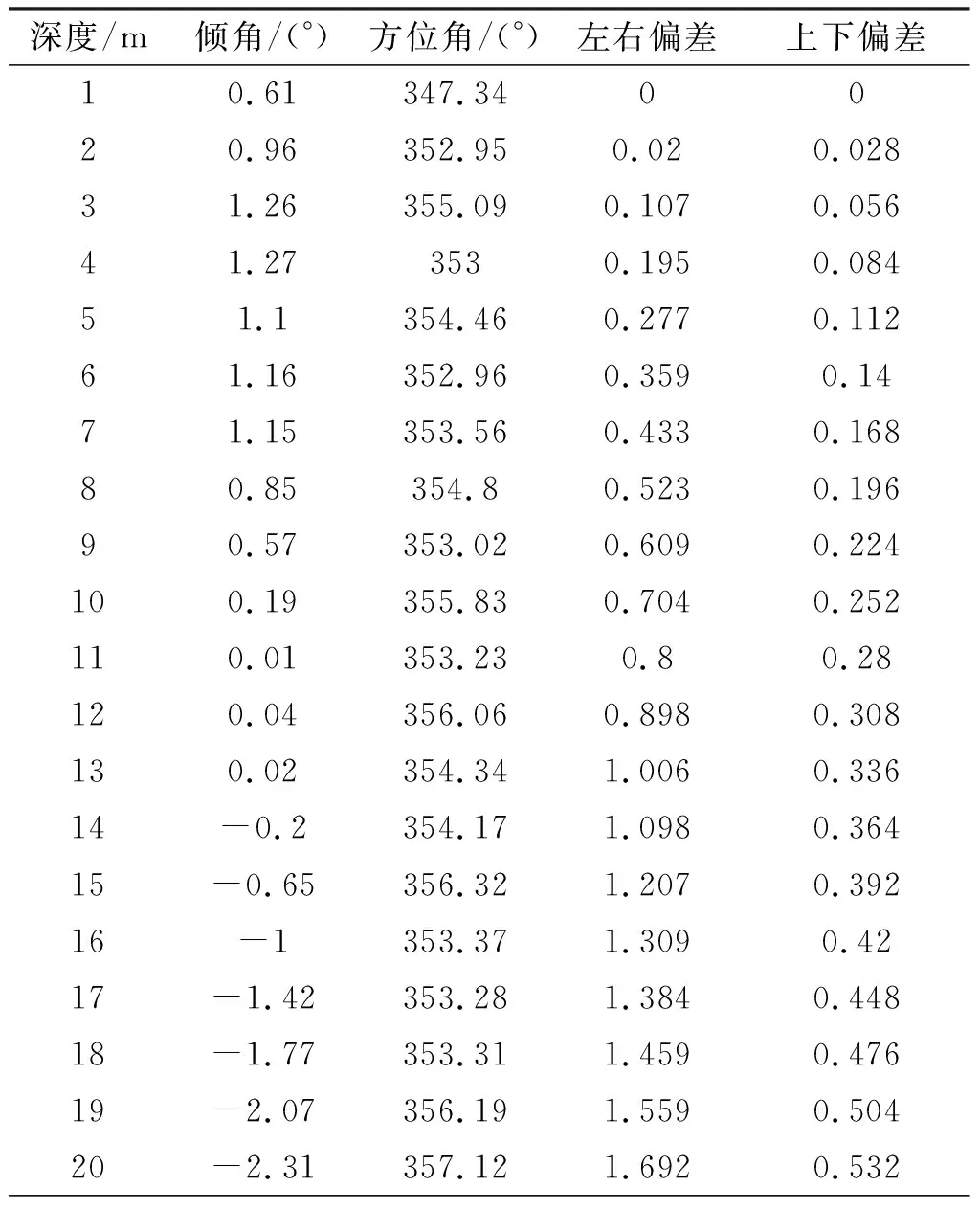
表1 钻孔数据

从图11中可以看出实钻终孔位置和设计终孔位置存在明显偏差，其中左右偏差从开始阶段就向右偏转，最终在终孔位置偏离1.692 m；上下偏差从起始阶段始相差0.028 m，至终点即20 m位置处相差0.532 m，在此过程中呈现递增趋势，表示实际钻孔轨迹从开始位置一直缓慢向下，逐渐偏离设计轨迹。上述测量数据与矿方已知数据完全一致，真实反映了钻孔轨迹的实际走势，对于矿方后续评价瓦斯抽采效果具有重要的实用价值。

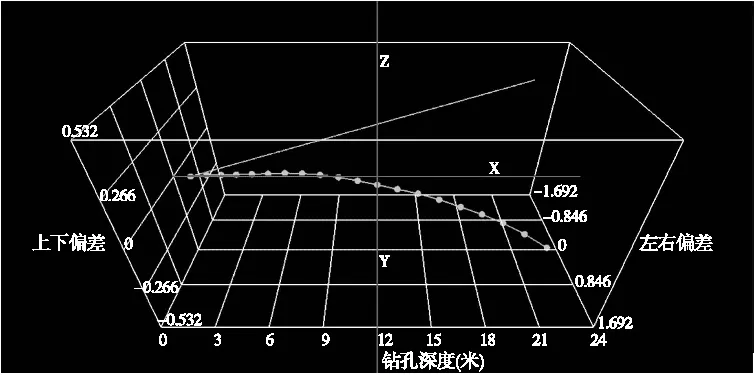
图11 三维钻孔轨迹空间示意图

7 结论

基于钻孔轨迹测量系统的工作原理，该文研制了基于PNI磁性传感器和MEMS加速度计的钻孔轨迹测量系统；为了提高钻孔轨迹测量系统的测量精度，该文分析了影响测量精度的误差类型、来源以及重要程度，并建立了两种加速度传感器和磁性传感器的误差修正模型实现钻孔轨迹测量系统系统的误差补偿。为了测试误差补偿算法的实际应用效果，分别采用了两种误差模型和不同点数对固定在测斜仪调校装置上的钻孔轨迹测量系统进行了误差补偿测试，验证了三阶正交矩阵配合高次多项式修正模型补偿效果要优于三阶正交矩阵配合零偏系数修正模型，且选用48位置时可兼顾精度和标定时间，倾角在-90°～90°的测量范围内达到±0.2°的测量精度，方位角在0°～360°范围内达到±1.5°。最后，为了测试钻孔轨迹测量系统的实际工作性能，该系统在晋能集团长治三元公司某矿进行了现场工业性试验，测量数据与矿方已知数据完全一致，真实的反映了钻孔轨迹的实际走势，得到了矿方的认可与好评，证明了该文研制的基于全空间误差补偿的钻孔轨迹测量系统完全满足煤矿市场的测量要求。