爆破片装置流阻系数数值仿真研究

孙少辰，叶 陈，丁信伟，许国锋

（1.沈阳特种设备检测研究院，辽宁 沈阳 110179；2.辽宁省安全科学研究院，辽宁 沈阳 110016；3.大连理工大学 化工学院，辽宁 大连 116024；4.哈尔滨商业大学 能源与建筑工程学院，黑龙江 哈尔滨 150028）

爆破片装置泄放量计算的方法主要有2种，分别为泄放系数法与流体阻力系数法（或称流阻系数法）。泄放系数法计算过程简单明了，但其使用限制条件多，未得到广泛应用［1-3］。流阻系数法计算过程考虑的影响因素比较全面，具有更加广泛的通用性和研究价值［4］。目前国外学者对爆破片装置流阻系数法的研究较多，研究的方法以理论和试验为主［5-12］。试验研究优点突出，只要给定输入条件就可通过测试直接得到结果。试验研究的缺点也很明显，在实验室建立试验装置进行试验，装置的规模和试验的温度、压力等条件都会受到限制。目前，大尺寸、高压力爆破片装置的流阻测试还无法在实验室完成。

近些年，计算机流体力学（CFD）发展迅速，应用CFD方法建模、通过模型进行数值仿真取得了多领域的技术进步和研究成果，但应用数值仿真方法研究爆破片装置流阻系数还未见报道。文中针对爆破片装置在管道内的泄放过程，进行了物理模型、数学模型、求解方法的研究和选择以及边界条件的设置，通过有效性验证研究论证了数值仿真方法的可行性，完成了管道内压力分布、速度分布和温度分布分析，总结了流体阻力产生的主要原因及其对爆破片装置动作的影响。利用数值仿真计算结果对不同类别、规格的爆破片装置的流阻系数值进行计算。

1 爆破片装置泄放过程数值模型及求解方法

1.1 物理模型研究

模拟爆破片装置在管道内泄放过程，首先要选择适合的湍流模型。选择时，不仅要考虑管内流体的湍流运动，还需要重视管道内壁面与流体之间的摩擦。管内壁面与流体之间边界层内流动是影响管内流体能量损失的重要因素之一。

出于多方面的需要，包括更好地对管内流体进行数值仿真计算、更准确地获得管内流体运动情况以及为爆破片设计提供精确的参数，模拟的过程中还需要考虑流体边界层与湍流区过渡过程的模拟。

连续性方程、N-S方程和能量守恒方程联用可以描述管内可压缩流体运动的详细过程，但是N-S方程的封闭求解需要先简化方程，减少未知参数，使方程数量与未知数量一致。简化可以采用多种方法，由此也产生了多种湍流模型。早期出现的湍流模型，例如k-ε湍流模型和k-ω湍流模型［13-15］，可以实现流体湍流流动的描述，但这些方程过度简化了N-S方程，造成对边界层的模拟误差较大，所以对边界层内流体运动的模拟效果不佳。之后出现的大涡模拟和雷诺应力等模型，不仅形式复杂而且需要进行多流体区域的网格划分，划分后的网格数量比较大，最终使得计算效率下降，时间消耗增大。

Transition SST模型［16-17］（又称为γ-Reθ转捩模型，以下简称转捩模型）将经验关联和间歇因子结合，将转捩动量厚度雷诺数Reθ作为控制边界层间歇因子γ的关联函数。由γ控制湍流生成，回避动量厚度的计算，通过输运方程实现计算当地化。

爆破片泄放过程涉及层流-湍流转捩、极强的逆压梯度和分离流问题，导致传统湍流模型无法对其准确预测。转捩模型对分离流动模拟的准确性较好，对于流场的压力分布具有更高的模拟精度［18-19］。因此，本文采用转捩模型对长管内流体运动进行分析，着重考虑管内几何尺寸突变时流体流动变化对能量损失的影响。

1.2 数学模型

1.2.1 控制方程［20］

可压缩稳态管内流动连续性方程表示为：

动量方程表示为：

能量方程表示为：

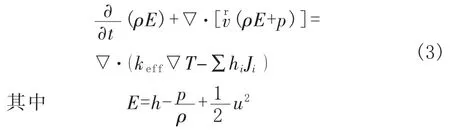
1.2.2 湍流模型

（1）SST k-ω湍流模型［21］SST k-ω湍流模型中关于湍流能k和比耗散率ω的输运方程表示为：

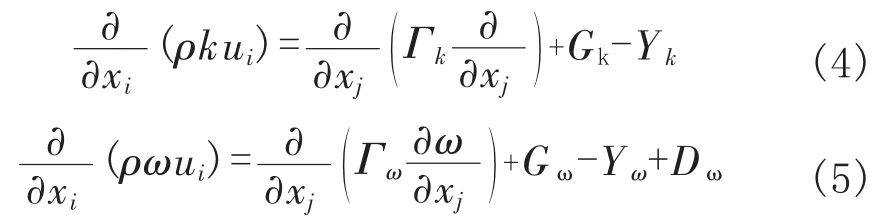
有效扩散系数可以表示为：

式（4）～式（7）中，k为湍流能，m2/s2；ω为比耗散率；ui为i坐标方向上的速度，m/s；Γk为 k的有效扩散系数，kg/（m·s）；Gk为湍流能的速度梯度，Gω为比耗散率的速度梯度,kg/（m·s3）；Yk为关于k的湍流耗散项；Γω为ω的有效扩散系数，μk为k湍流黏性系数，kg/（m·s）；Yω为关于ω的湍流耗散项；Dω是交叉扩散项；σk为k的湍流普朗特数，σω为ω的湍流普朗特数，具体各项定义详见文献［21］。

（2）转捩模型 转捩模型由流动间歇因子γ的输运方程及经验公式结合SST k-ω湍流模型构成。将流体处于湍流状态和层流状态的时间比例定义为流动间歇因子，用符号γ表示。用γ值控制湍流生成，γ=0时为层流，γ=1时为湍流。当转捩开始时，γ开始增加。

1.3 数值求解方法

爆破片的泄放过程为可压缩稳态管内流动，而且求解问题时网格要比较密，因此采用密度基的隐式方法进行求解，通量用Roe-FDS格式，可以耦合求解能量和动量方程，能比较快地得到收敛解。

1.4 边界条件设置

爆破片装置泄放过程比较快，流体与管壁之间的摩擦剧烈，流动的动能将会转化为热能，但是热能在比较短的时间内无法及时释放到大气中，因而在壁面附近累积。据此，设置管壁表面为绝热壁面，热流量为0 W/m2。入口设置为压力入口，具体数值由仿真条件给定。出口设置为压力出口，泄放管道出口的实际条件压力为大气压力。

2 爆破片流体阻力测试系统数值模型及其有效性验证

2.1 系统构成

根据GB/T 567.4—2012《爆破片安全装置第4部分：型式试验》［24］中的要求建立由缓冲罐、测试管路和泄放管路等组成的流阻测试系统，见图1［25］。

图1 爆破片流体阻力测试系统图

其中，缓冲罐为立式储罐，封头顶部有导流板，罐体安装了温度计和压力表。测试管路由圆形管道以及安装在其上的收集容器、压力传感器、补偿器、音速喷嘴、温度传感器、滞止容器、排污阀、开关阀、调压器等组成。泄放管路入口到取压口A的距离为60倍管径D，取压口A与取压口B的距离为30倍管径，爆破片装置安装在取压口B与取压口C之间，取压口C到取压口D的距离为30倍管径，取压口D到出口距离为15倍管径。

缓冲罐与泄放试验管道通过过渡管连接。过渡管具有减少连接口局部阻力的作用，其结构见图2。

图2 过渡连接管示图

2.2 模型及网格

对泄放管道及爆破片建模，见图3。对爆破片及泄放管到进行网格划分，见图4。

图3 泄放管路几何模型示图

图4 爆破片和泄放管模型及网格示图

图4中，泄放管道采用六面体网格划分，爆破片采用四面体网格划分。爆破片采用不同的网格划分，主要是基于其几何形状考虑。爆破片的几何形状不规则，很难生成规则六面体网格，而四面体网格的生成却不受几何形状的限制，只要通过简单设置即可生成比较好的网格。四面体网格的使用会使网格总数增加，但还不足以造成计算速度的降低。

2.3 有效性验证

以理论计算值［7］和试验值为对比项进行数值模型有效性验证。按照爆破片流阻系数法计算理论值，用流阻试验系统测定试验值。为了提高管内压力分布的可比性，将爆破片装置安装到过渡管与泄放试验管之间。

2.3.1 初始条件

数值仿真计算初始条件设置见表1。其中，比热比为绝热指数，即定压比热容与定容比热容之比。表1中的容器对应图1的缓冲罐。

表1 数值仿真计算初始条件设置

2.3.2 泄放管内压力分布比较

泄放管入口压力p=1.72×105Pa和p=2.78×105Pa时，管道内部压力分布的模拟值、试验值与理论值对比结果见图5。

从图5中可观察到，试验结果与数值仿真结果的拟合度非常好。4个测压点，取压口A、B、C、D的数值仿真结果和理论分析结果之间误差不大于0.1%。在不同入口压力条件下，数值计算能够模拟出实际管内流体运动情况。

从图5中还可观察到，理论计算与数值仿真结果有误差，根据图5计算的误差保持在15%以内，更大的误差出现在爆破片装置所在的位置。理论计算数据不能直观表现出局部阻力损失情况，但是，数值仿真能够很好地体现爆破片装置产生的局部阻力损失。

图5 不同入口压力条件下模拟值、试验值与理论值比较

总体上讲，数值仿真结果和试验结果吻合较好，所得数据能够反应出管内的压力变化情况，进而可以将数值仿真计算推广到更大直径管道或更高压力情况下的爆破片装置流阻系数计算中。

3 爆破片装置流阻分析

3.1 压力分布

泄放管路内流体压力分布见图6。由图6a的总体分布图可以看到，泄放管路入口段的流体压力变化明显。这种变化与泄放管路入口段安装了爆破片装置有关。由图7b的局部放大图可以看到，爆破片装置所在位置（黑色竖线所示位置）压力突然减小，流体通过爆破片装置后，压力会逐渐下降，直至在出口压力降为大气压。

结合图6与流体在泄放管道内的流动过程进行分析可知，破裂后的爆破片贴附在管壁上，改变了管道形状，造成管道内流道变窄，形成局部阻力，阻碍流体运动，进而改变流动状态，形成紊流。在没有管件阻碍流体运动情况下出现管内压力降低，是管内流体与沿程壁面之间的摩擦损失造成的。

图6 泄放管路内部流体压力分布

3.2 速度分布

泄放管路内流体流速分布见图7。由图7a的总体分布图可以看到，泄放管路入口段的流体速度变化明显。这种变化与泄放管路入口段安装了爆破片装置有关。由图7b的局部放大图可以看到，在爆破片装置区流体流速快速增大，经过爆破片后流体流速增幅变小。

结合图7与流体在泄放管道内的流动过程进行分析可知，流体经过爆破片时，管径的突然减小，使得流体速度增加，流速增加将改变流体运动方向，增加粒子之间的相互碰撞，降低流体的能量。流体在泄放管路出口位置的流动速达到了246.9 m/s，对应的马赫数为0.77，未达到超音速，但此条件下管内流体已经表现出了较强的可压缩性，因此在计算过程中需要考虑气体密度的变化引起的其他物理量的改变。

图7 泄放管路内部流体速度分布

3.3 温度分布

泄放管路及管内流体温度分布见图8。由图8a可以看到，泄放管路入口段的温度变化明显。这种变化与泄放管路入口段安装了爆破片装置有关。由图8b可以看到，在爆破片装置位置，管内流体温度显著低于管壁温度。

结合图8与流体在泄放管道内的流动过程进行分析可知，在爆破片位置，流体速度突然变大，管内流体能量损失随之增大，而管壁选用的壁面条件为绝热壁面，不与环境有能量交换，损失的能量在管壁附近累积，同时管内流体速度高于管内壁流体运动速度，管壁处累积的能力对管内流体加热效果不明显，造成爆破片装置区管内流速大、温度低、管壁温度较高。当流体到出口附近时，虽然流体速度在增加，但是经过较长时间的加热，管内流体的温度会有所增加，但增加幅度较小。

图8 泄放管路内部流体温度分布

3.4 爆破片装置流阻系数计算

爆破片装置流阻系数计算程序为，先采用数值仿真方法对指定型式爆破片装置泄放过程进行研究，获得取压口处的压力和质量流量等参数值，然后使用 GB/T 567.4—2012［24］中的公式对爆破片装置的流阻系数进行计算，最后根据数值仿真结果对不同类别、规格爆破片装置的流阻系数进行计算。

基于表1参数、数值仿真结果，应用流阻系数计算公式计算的不同类别、规格爆破片装置流阻系数见表2。

表2 爆破片装置数值仿真计算结果

4 结语

爆破片装置种类繁多，流阻试验系统不能对大尺寸、高压力的爆破片装置进行测试。研究了建立爆破片装置泄放过程数值模型，通过模型仿真管道内爆破片装置泄放过程，利用模型仿真结果计算爆破片装置流阻系数的可行性和可靠性。研究结果表明，计算的爆破片装置流阻系数可对试验测试范围进行扩充，弥补试验条件的限制，为爆破片装置泄放能力的判定提供有效依据。