基于Timoshenko梁的温度力作用下的钢轨振动特性研究

王轲，蔡有杰，孙庆明，常焱森

基于Timoshenko梁的温度力作用下的钢轨振动特性研究

王轲，蔡有杰，孙庆明，常焱森

（齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006）

根据Timoshenko梁理论及车辆-轨道耦合动力学理论考虑剪切变形所引起的转动惯量，建立轴向载荷作用下无砟轨道钢轨振动有限元模型。并在理论分析的基础上, 通过建立的实验模型对不同温度力作用下钢轨振动特性进行了实验研究。结果表明，所建立的理论模型能够比较准确地反映无砟轨道钢轨在温度力作用下的主要振动特征，以及温度力和振动特征之间的关系。对应用振动特性研究无砟轨道钢轨的温度力和评估轨道安全可靠性有一定的指导意义。

无砟轨道；Timoshenko梁；温度力；钢轨

随着列车运行速度日益提高，以“高平顺”和“少维修”为目的的无砟轨道应用越来越广泛，已成为高速铁路的主要结构形式。然而，由于该类结构原因，线路运营过程中钢轨温度发生改变，导致了无砟轨道钢轨内产生较高的纵向温度力。在这种情况下，钢轨温度力的检测在铁路安全监测中显得越来越重要。

在研究轨道结构特性时，一般通过一定的简化，将钢轨描述为离散为等间距弹性支承上质量均匀分布的无限长的Euler梁或Timshenko梁。国内外学者对于梁[1,2]和有轴向力的梁[3,4]结构进行了大量的研究，并在轨道振动分析中引入钢轨梁模型研究无温度力轨道的振动[5-7]。罗[8]采用能量法研究了温度应力影响下的轨道振动特性。高[9]将钢轨处理为Euler简支梁后建立钢轨子系统和轨下结构子系统的三维有限元模型并计算动力响应。雷[10]的轨道结构模型中分别将钢轨、轨道板和混凝土支承层简化为Euler梁和Timshenko梁，对模型进行振动分析认为Timshenko梁模型在中高频范围适应性更好。左[11]以Timoshenko梁钢轨建立基于格林函数法的车辆-轨道耦合振动分析模型，分析车辆、轨道各子系统振动响应。由以上可知，国内外针对不同梁模型的轨道结构振动响应变化方面的研究较多，但从结构动力响应的角度开展对钢轨温度应力进行分析的研究鲜见。

针对无砟轨道结构，由于钢轨支承刚度较大且间距较短，一般为0.6～0.65m，故而需要考虑剪切变形和转动惯量对振动响应的影响，采用 Timoshe-nko 梁作为钢轨模型比 Euler 梁轨道模型可以获得更为精确的结果[12]。本文以Timoshenko梁的理论为基础，采用有限元方法从理论上来分析内部温度力作用下钢轨的振动特性，并以1∶1实尺模型进行了模拟试验对比分析。针对轨道结构钢轨温度力的检测，通过对轨道结构施加脉冲激励，根据钢轨在不同温度力状态下的振动响应特性，研究振动响应与钢轨温度力之间的关系，并为温度力检测提供技术支持。

1 振动分析

1.1 力学分析

本文模型采用Timshenko梁的理论为基础，分析温度力作用下钢轨的振动模型。研究过程做如下假设：（1）松开拉伸钢轨后，钢轨的位移小且在平面内。（2）钢轨横截面始终保持平面。（3）冲击振动试验时内部温度应力保持不变。

考虑到车轮和轨道是一个大的耦合系统，轨道结构中将钢轨简化为位于弹性点支承上的Timoshenko梁，扣件系统则以离散分布的阻尼弹簧表示[3]。如图1，()为单位长度动荷载，()为扣件处支反力，则钢轨整体受力如图1(a)，第跨微段d受力如图1(b)及变形如图1(c)，图示中的负号表示与图示箭头标示方向相反。

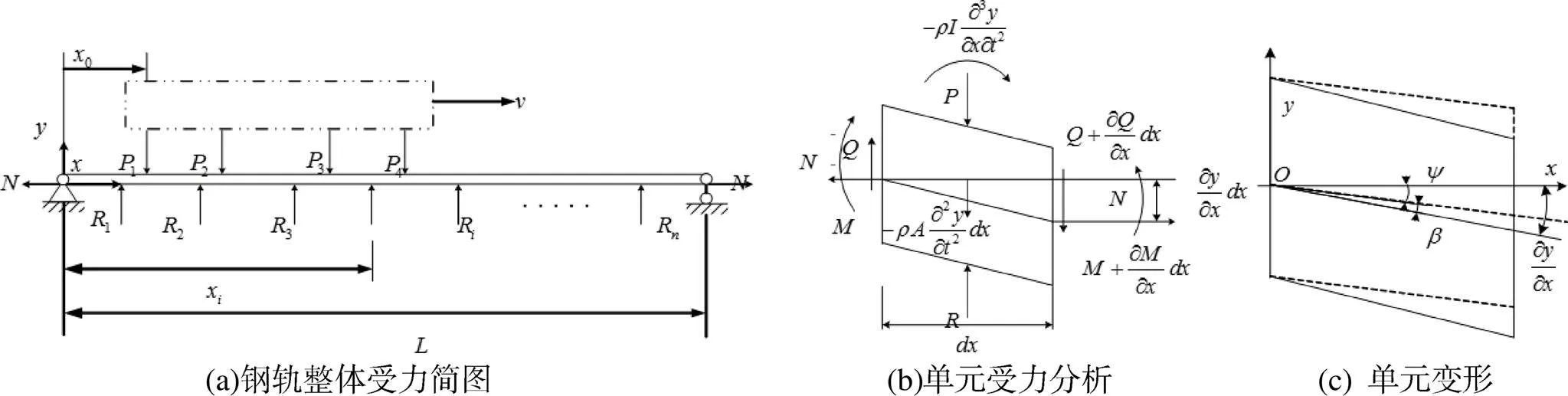
图1 钢轨单元受力简图

根据材料力学和结构力学理论有：

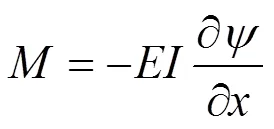
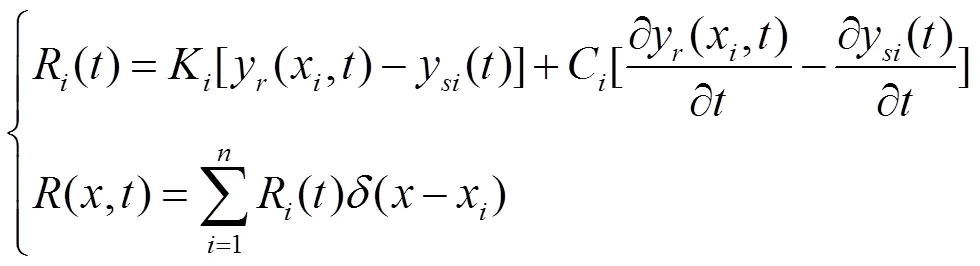
1.2 振动方程

由图1，可得微元段转动和平动微分方程分别为

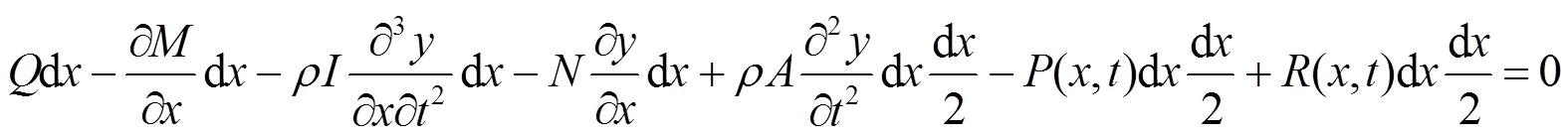
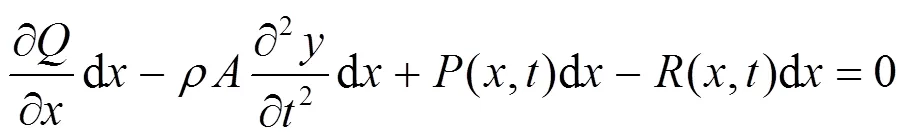
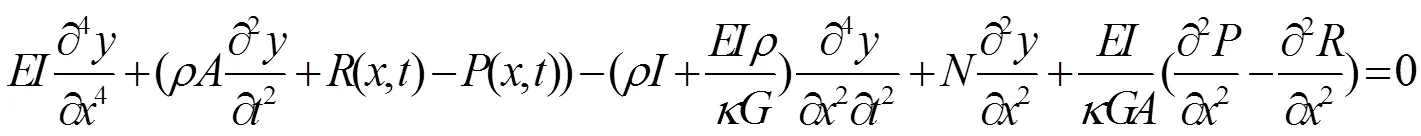
则轴向力作用下钢轨自由振动微分方程为

无轴向力作用即=0时，可得

式(9)为经典Timoshenko梁振动微分方程。可见略去剪切变形引起的转动惯量后将会产生关于时间的四次导数项，计算自振频率时会出现与剪切变形有关的固有频率[13]。

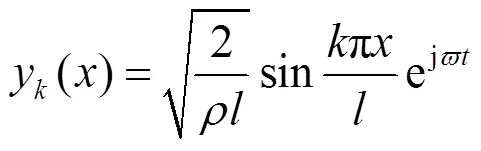
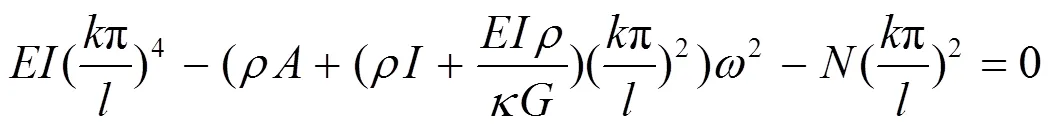
解之得Timoshenko梁固有频率为

2 模拟实验

2.1 实验原理

由于约束钢轨伸缩，当轨温变化时钢轨无法自由伸缩而产生内部温度力；钢轨受到拉力时，长度发生变化，其内部产生拉应力。如此，可以拉伸钢轨，使得其内部产生拉应力，用来模拟温度应力。为了确保拉伸力准确，则读取钢轨拉伸机油压表应尽可能准确，故而分别采用10, 20, 30MPa的压力进行拉伸，对应钢轨拉伸力为180, 360, 540kN。

拉伸力和温度变化量计算公式：。

式中，为钢轨线性膨胀系数，为温度变化量。计算结果如表1。

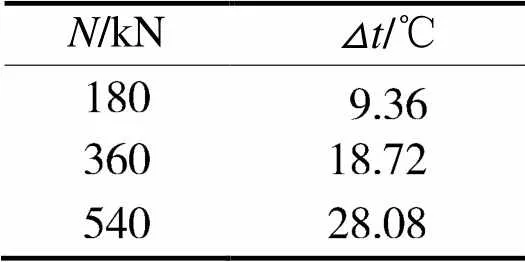
表1 温度力与温度变化量

2.2 实验方案

地面以下铺设钢筋骨架后灌注混凝土制成混凝土基座，基座凝固后铺设四块CRTS—I型轨道板，调平后灌注CA砂浆，并在轨道板接缝处灌注树脂，再铺设钢轨，用WJ-7型扣件锁紧钢轨，并在钢轨两端设置固定机构控制位移。试验台不仅采用高铁专用的构件而且依据TB10621：2009和TB10754：2010进行安装和检查。切割钢轨并使断缝宽度大于30mm。在轨缝处安装钢轨拉伸机，施加一定的拉力拉伸钢轨后锁紧扣件并将拉伸机保压来模拟钢轨产生内部温度应力。该方案模拟了无砟轨道结构，不仅减小了现场试验成本，而且保证了实验的可控性和可重复性。

图2 钢轨力学实验平台

2.3 实验步骤

如图3所示对钢轨进行锤击实验。激励点在轨中轨顶，传感器数据采集位置应避开钢轨振动节点处，采样频率为12800Hz。

图3 锤击实验

实验分为4个步骤：

（1）释放温度施力装置和所有钢轨扣件，释放钢轨内部温度应力。

（2）使用规定的拉力（分别为0, 180, 360, 540kN）拉伸钢轨，并保持恒定，以模拟钢轨中的温度力。

（3）当轨道稳定时，锁定所有轨道紧固件。钢轨内应力可以模拟钢轨在温度变化时产生的温度力。

（4）在保持拉力恒定的情况下进行试验。在不同拉力下重复上述步骤，可以得到钢轨在不同温度力下的振动数据。

3 结果分析

3.1 计算参数

利用建立的理论模型进行分析，采用轨道参数如下：钢轨类型=60kg/m，弹性模量=2.1×108kN/m2，剪切模量=78.48×106kN/m2，惯性矩=32.17×10-6m4，剪切系数=0.34[14]，截面面积=77.45×10-4m2。

利用理论模型计算分析和实验装置模拟实验可获得钢轨在不同轴向力下各阶模态。

3.2 实验结果与计算结果分析

如图4，不同轴向力下频率变化率((不同温度力)–(无温度力))/(无温度力)），纵向拉力逐渐升高过程中即轨温变化量逐渐增大过程中一阶频率变化率分别为44.22%, 77.76%和105.9%，三阶频率变化率分别为5.83%, 11.35%和16.62%而十阶频率变化率分别为0.538%, 1.074%和1.607%。随着模态阶数的升高，频率的变化越来越小。对比实验结果可知，温度力对钢轨低频影响较为显著，高频较弱。

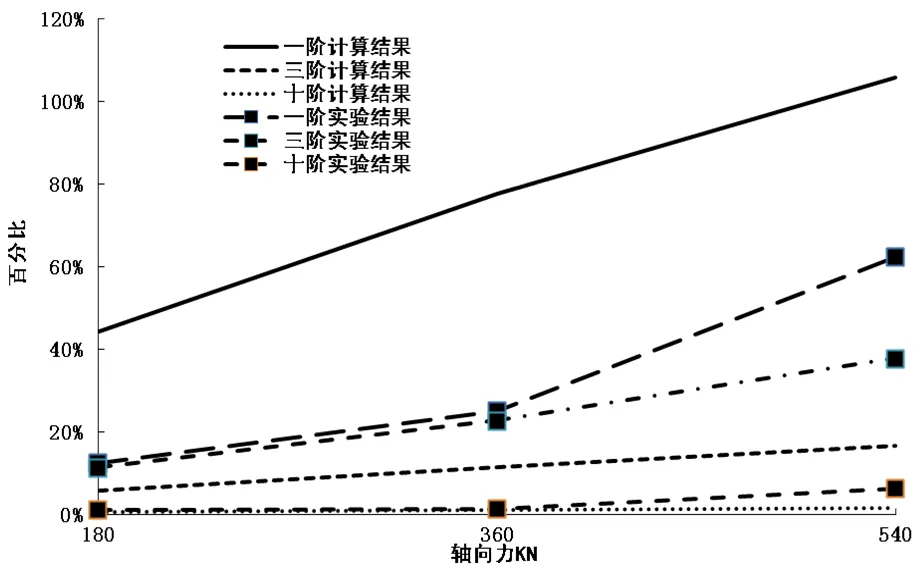
图4 不同轴向力下频率变化率

如图5，不同温度力作用下，理论分析结果与实验结果相似，钢轨自振频率随着温度力的变化而发生改变，温度力增加时其自振频率也会相应增高，反映了结构的基本特性，且无论从计算公式还是实验结果都表明其自振频率与温度力的变化的是近似线性关系。

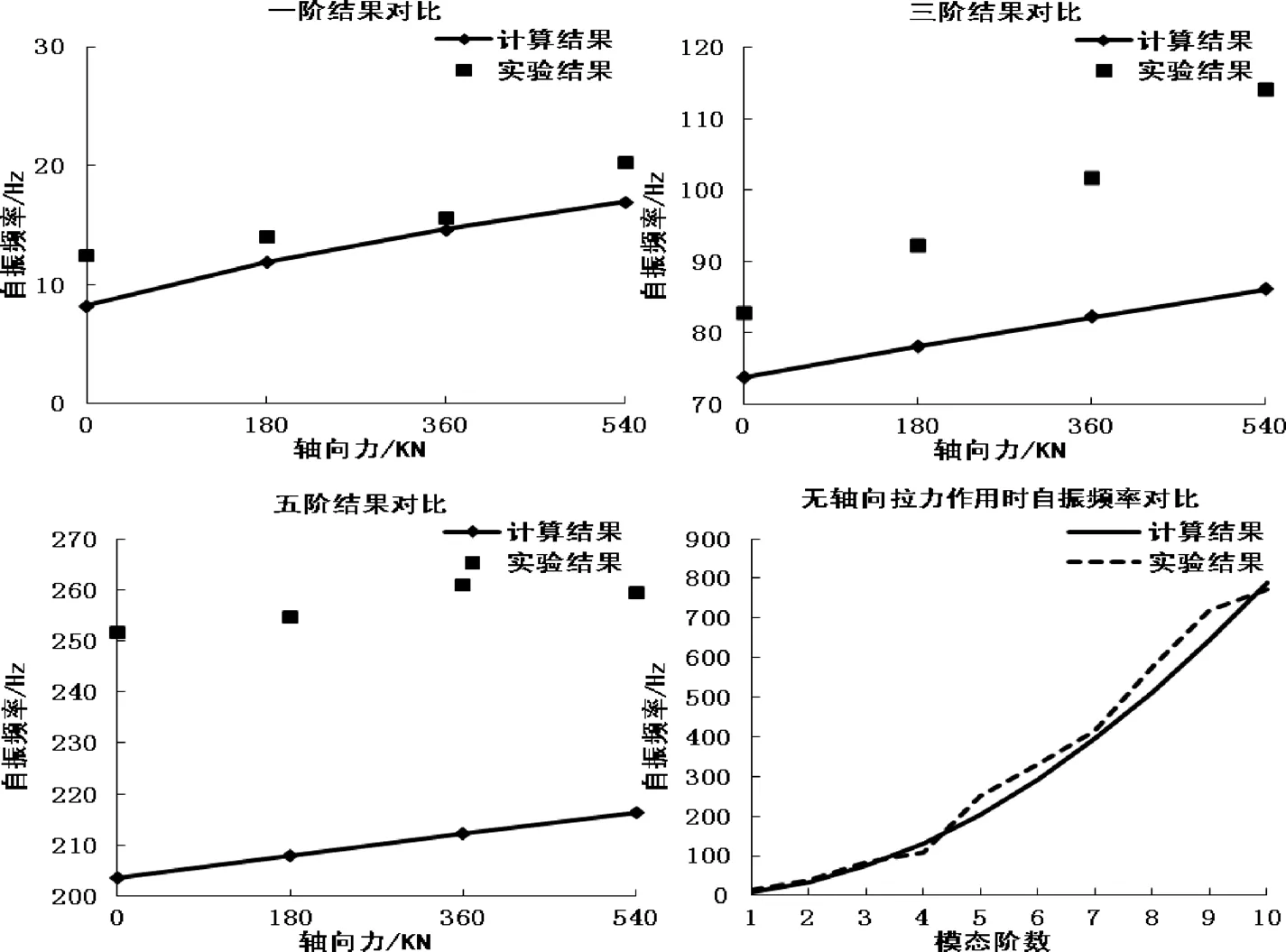
图5 不同轴向力时各阶频率

4 结论

本文在Timoshenko梁理论及车辆-轨道耦合动力学理论的基础上，建立了考虑梁剪切变形引起的转动惯量的轴向拉力作用下钢轨振动模型，通过理论分析结果和模拟实验对温度力作用下钢轨动态特性进行了研究。结果表明，随着轴向拉力的增大即温度力增加使得各阶频率增高，尤其是低频阶段增幅更为明显，温度力的变化对钢轨低频振动特性影响显著，两者呈非线性关系；轴向拉力的增大即温度力增加使得同阶频率增高，且与温度力增加呈现近似线性关系。综上，本文所建立的理论计算模型能够较为准确的反映无砟轨道结构在温度力作用下的振动特性，可为研究钢轨温度力检测和安全监测提供一定的技术支持，为进一步开展研究无砟轨道稳定与安全性提供帮助。

[1] R.克拉夫. 结构动力学[M]. 2版.北京：高等教育出版社，2006: 284-286.

[2] HAN SM, BENAROYA H, WEI T. Dynamics of transversely vibrating beam using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988

[3] I. SVENSSON. Dynamic response of a constrained axially loaded beam[J]. Journal of Sound and Vibration, 2002, 252(4): 739-749.

[4] YUSUF YESILCE, OKTAY DEMIRDAG. Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems[J]. International Journal of Mechanical Sciences, 2008, 50: 995-1003.

[5] WU TX，THOMPSON DJ. A double timosh enko beam model for vertical vibration analysis of railway track at high fr equencies[J]. Journal of Sound and Vibration, 1999,219( 5): 881-904.

[6] Chen, YH; Huang, YH; Shih, CT. Response of an infinite timoshenko beam on a viscoelastic foundation to a harmonic moving load[J]. Journal of Sound and Vibration, 2001,241( 5): 809-824.

[7] 翟婉明. 车辆-轨道耦合动力学[M]. 2版. 北京：中国铁道出版社，2002: 20-33.

[8] 罗雁云，朱剑月，冯奇. 不同温度力下无缝线路钢轨振动特性分析[J]. 力学季刊，2006, 27(2): 279-285.

[9] 高芒芒，李国龙，杨飞，等. 基于强迫振动的列车-轨道-轨下结构垂向耦合动力分析方法及工程应用[J]. 中国铁道科学，2021, 42(2): 50-58.

[10] 雷晓燕，邢聪聪，吴神花. 轨道结构中高频振动特性分析[J]. 振动工程学报，2020, 33(6): 1245-1252.

[11] 左志远，刘林芽，秦佳良，等. 扣件胶垫温变特性对车辆-轨道垂向耦合动力响应的影响分析[J]. 噪声与振动控制，2020, 40(3): 194-199,206.

[12] HAMET J F. Railway noise: Use of theTimoshenko model in rail vibration studies[J]. Acustica, 1999, 85: 54-62.

[13] 陈镕. Timoshenko梁运动方程的修正及其影响[J]. 同济大学学报（自然科学版），2005, 33(6): 711-715.

[14]K. KORO, K. ABE, M. ISHIDA, et al. Timoshenko beam finite element for vehicle-track vibration analysis and its application to jointed railway track[J]. Proceedings of the Institution of Mechanical Engineers, Part F. Journal of rail and rapid transit, 2004, 218(f2): 159-172.

Influence of temperature stress to rail vibration characteristics based on Timoshenko beam

WANG Ke，CAI You-jie，SUN Qing-ming，CHANG Yan-sheng

(School of Mechanical and Electrical Engineering, Qiqihar University, Heilongjiang Qiqihar 161006, China)

Based on the theory of Timoshenko beam and vehicle-track coupling dynamics, considering the rotational inertia caused by the shear deformations of the beam, a finite element model of axial loads on rail in ballastless track was established.On the basis of theoretical analysis, experimental study of the rail vibration characteristics of ballastless track under different axial force was carried out through an experimental model. The results reflected basically the main vibration characteristics of the rail under different temperature force. The model is useful for the research of the relationship between the temperature stress and the vibration characteristics of rail. It can be applied to predict the safety and reliability of rail under different temperature stress using rail vibration characteristics.

ballastless track；Timoshenko beam；temperature force；rail

2021-11-17

2019年度黑龙江省省属本科高校基本科研业务费面上项目（135409226）；2019年齐齐哈尔大学教育科学研究项目（Z201903）

王轲（1980-），男，河南新乡人，讲师，博士，主要从事振动分析应用研究，wangke@qqhru.edu.cn。

U270

A

1007-984X(2022)05-0052-05