对一道解析几何联考试题的拓展探索
2022-06-16 06:30:30江苏省徐州市第一中学221004江苏省高中数学名师工作室213001张培强
中学数学研究(广东) 2022年9期
江苏省徐州市第一中学(221004)江苏省高中数学名师工作室(213001)张培强
1 问题呈现

2 解法探究




3 拓展探索
3.1 将双曲线一般化



3.2 将直线一般化



(1)求C的方程;(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
考题1 中,由直线P2A与P2B的斜率的和为-1 可得直线AB过定点;考题2 中,由直线AB过定点可得直线MA与MB的斜率的和为0;考题3 中,由直线AM与AN的斜率的积为-1 可得直线MN过定点.那么,在命题3 中,M,N两点关于坐标原点对称的背后是否有直线AP与AQ的斜率之间存在某种关系?
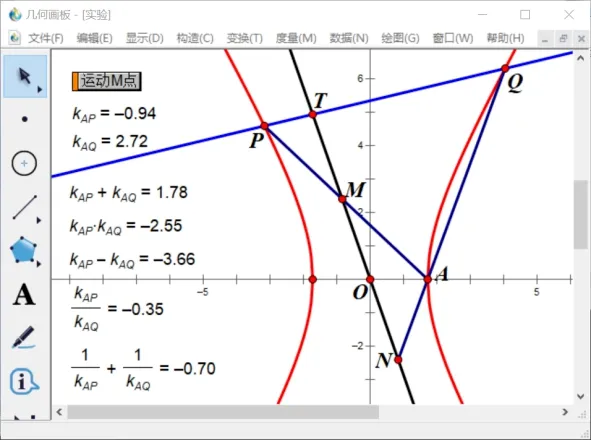


3.3 将点一般化



3.4 圆锥曲线的统一性质

猜你喜欢
中学生数理化·自主招生(2022年2期)2022-05-30 10:48:04
中学生数理化(高中版.高考理化)(2022年2期)2022-04-26 14:01:52
中学生数理化·中考版(2021年12期)2021-12-31 03:24:36
中学生数理化·中考版(2021年11期)2021-12-06 07:29:12
中等数学(2020年4期)2020-08-24 08:08:40
中学数学杂志(2019年1期)2019-04-03 00:35:36
高中生·天天向上(2018年3期)2018-04-14 09:39:52
学生天地(2017年4期)2017-05-17 05:48:29
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16 05:33:43
高中生·天天向上(2016年8期)2016-11-22 09:22:46

