等积变换在圆锥曲线中的应用

浙江省兰溪市第一中学(321102)张城兵

一、问题提出

在圆锥曲线解答题中除了求一些基本量如斜率(直线方程)、参数范围,证明直线恒过定点外,还有一类涉及单个图形面积或多个图形面积的和、差、积、商的最值或取值范围问题“上镜率”较高,难度较大.因为面积的求解牵涉到的知识点面广且错综复杂,计算量大,如果讲求技巧,硬算到底会费时费力,得不偿失;若能适时适地用上等积变换知识,可以将难求的图形面积转化为易求图形的面积,大大减少运算量,提高解题正确率.

由于教学的侧重点和中考要求,等积变换知识在初中里有所提及,甚至也是考试的重点,但有些就比较偏,学生相对陌生.进入高中时衔接教学可能顾及不到,还有高中课程涉及平面几何教学内容较少,偶尔碰到也就题论题,不见得系统化,即使圆锥曲线中要用到,也不会专门组织教学.笔者发现这类涉及面积的题目若能用上等积变换知识,如虎添翼.现将基础知识作一介绍再选取各具特色的7 道例题逐一剖析:

二、基础知识

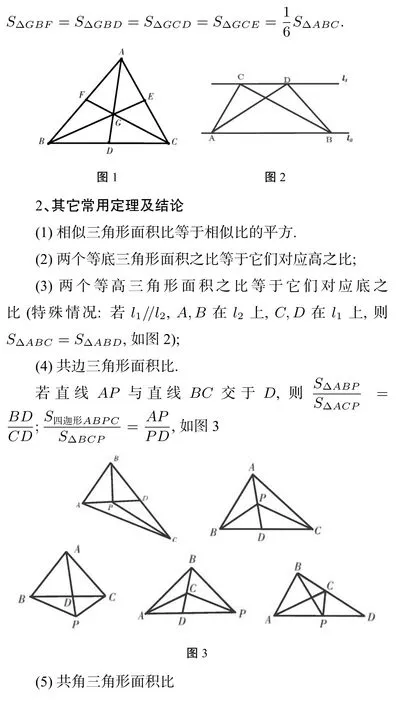
三、精选例题

四、结束语

笔者收集剖析的7 个例题,囊括了常见有关面积的解答题,若能在平时训练中“先用几何眼光观察与思考,再用坐标法解决的策略”,举一反三,解决这类问题就容易上手.当然用了等积变换知识还必须具备设参、用参、消参及其计算能力等综合素养,否则也难到达成功彼岸,另外求三角形面积有各种方法,可以参见笔者拙文[1].