热喷干扰气体模型对飞行器气动特性影响分析1)

傅杨奥骁 刘庆宗 丁明松 江 涛 李 鹏 董维中 许 勇 高铁锁

(中国空气动力研究与发展中心,计算空气动力研究所,四川绵阳 621000)

引言

喷流反作用控制系统(reaction control system,RCS)是目前很多高超声速飞行器进行跨流域飞行时所采用的气动控制方法,相比于常规的气动舵面控制技术,具有响应快、不受空域限制的优点[1-2],可明显提升高超声速飞行器跨流域飞行的控制和机动能力.

当喷流反作用控制系统工作时,发动机产生的喷流将与来流发生强烈的相互作用,产生一系列复杂的流场结构,这种现象被称为喷流干扰效应[3-4],会对飞行器气动力热特性产生很大影响.在实际工程应用中,喷流反作用控制系统一般采用小型火箭发动机,喷管出口为高温燃气,一般称之为“热喷”,与之相对的是在风洞试验中,出于成本和可实现性的考虑,常常采用空气作为喷流气体进行试验,由于其温度一般较低,因此被称为“冷喷”.喷流燃气的气体性质与常温空气有较大差别,同时,喷流燃气中未完全燃烧的组分进入主流后还会发生二次燃烧现象[5-6],使喷流干扰问题更加复杂,这些现象可统称为热喷干扰效应.

目前,已有一些学者针对热喷干扰效应开展了相关研究.在这些研究中,很大一部分采用了二元等效比热比异质流模型进行计算:如文献[7]采用二元等效比热比异质流模型,研究了尖锥外形的热喷干扰问题;Shingo 等[8]针对火星着陆器外形,采用此类模型研究了着陆器RCS 喷流干扰对气动力特性的影响;赵弘睿等[9]针对拦截弹外形,采用类似方法研究了高空环境下的侧向喷流干扰问题.还有部分学者采用化学反应冻结流对热喷干扰问题进行了研究:如Votta 等[10]采用化学反应冻结流数值模拟了火星着陆器的喷流干扰问题;DeSpirito[11]采用此模型研究了热喷干扰问题中湍流模型的影响.由于在风洞中采用空气进行冷喷试验成本低、重复性好、易于实现,部分学者尝试采用空气喷流来模拟燃气热喷流,如林薄希等[12]采用空气完全气体模型,研究了喷流干扰气动热数值模拟的相似准则问题.以上研究中采用的多种气体模型,均对实际的燃气热喷干扰问题进行了不同程度的简化,可以明显提高计算效率,但在一定条件下,同样可能引入误差,不能准确反映真实的物理情况.因此,一些学者采用了较为精细的气体模型进行研究,如Li 等[13-14]采用化学反应流模型对火箭级间热分离流场进行了数值模拟,结果显示喷流燃气的化学反应对喷流干扰区范围有很大影响,但文中同样指出,采用该种模型计算需要巨大的计算资源;Dong 等[15]采用类似模型对锥柱裙外形的热喷干扰流场进行了数值模拟,结果显示燃气化学反应对分离区长度具有重要影响;赵法明等[16]基于类似模型对钝锥外形的喷流干扰流场进行数值模拟,结果显示热喷燃烧效应会引起喷流干扰流场结构变化,进而影响飞行器的气动力特性.

可见,目前对于热喷干扰问题的研究,从提高计算效率的角度出发而采用各种简化模型,可以解决大规模计算的问题,但在某些条件下可能引入误差;从更加全面地考虑问题的角度出发而采用精细模型计算时,其计算效率往往很低.在各种条件下,综合考虑计算效率和计算精度而对气体模型做出选择,是工程应用中所面临的问题,因此有必要系统地考察不同气体模型对热喷干扰流场数值模拟结果的影响,为实际工程应用提供参考.

本文针对典型外形的RCS 热喷干扰问题,基于自主研发的气动物理流场计算软件AEROPHFlow 以及喷流燃气物理化学模型,分别采用化学反应流、反应冻结流、二元异质流以及空气喷流四种气体模型进行了数值模拟,分析了不同气体模型对热喷干扰流场结构及飞行器气动力热特性的影响,同时考察了不同马赫数、飞行高度下的变化规律.

1 数值计算方法

流场控制方程采用包含化学反应源项的三维Navier-Stokes 方程,其无量纲化形式如下[17]

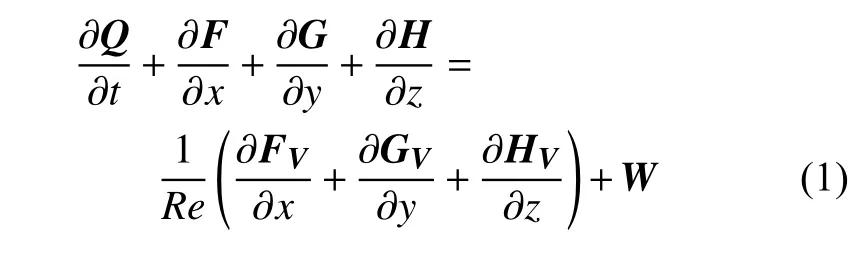
式中Q是守恒变量,完全气体模型Q=(ρ,ρu,ρv,ρw,ρE)T,化学反应流、反应冻结流及二元异质气体模型.其中ρ是混合气体总密度,ρi是组分i的密度,u,v,w为直角坐标下三个方向的速度,Et为气体内能,Re是雷诺数,F,G,H和FV,GV,HV分别对应了三个方向的对流项和黏性项,W为化学反应源项.

采用结构网格的有限差分方法离散控制方程(1),对流项采用AUSMPW+格式离散,黏性项采用中心差分格式离散,湍流模型采用k-ωSST 模型[18],时间离散采用LU-SGS 隐式方法.具体处理方法详见文献[17,19].

2 气体模型

2.1 化学反应流模型

RCS 发动机产生的高温燃气进入外流空气流场后,首先需要考虑高温下空气组分发生的离解、复合和置换等化学反应,同时,由于燃气中含有一些易燃组分,其进入空气后还会发生一系列复杂的二次燃烧反应,而本文采用的化学反应流模型则考虑了上述复杂化学反应.

由于喷流燃气中的液体相杂质占比很小,对干扰流场的影响很小,因此这里忽略燃气喷流中少量液体相杂质的影响.采用的化学反应模型如表1 所示,其中包含了空气以及燃气组分在高温下发生的离解、复合、置换等化学反应,表中M 代表碰撞体.各反应的反应速率通过Arrhenius 公式计算,系数常数取自文献[20-25].

表1 化学反应模型Table 1 Chemical reaction model

流动过程中,化学反应的模拟通过流动方程与化学反应源项的强耦合自动实现,源项中i组分生成源项wi可写为

式中,Nr为模型中化学反应个数,Mi和Qj分别为第i组分的分子量和第j化学反应的生成源项,和γij分别为第j反应中第i组分的生成物系数和反应物系数.

2.2 化学反应冻结流模型

本文采用的化学反应冻结流冻结了燃气组分相关的化学反应,即将喷流燃气视为不反应的多组分化学惰性气体,只考虑来流空气组分在高温下发生的各种化学反应,以简化问题并提高计算速率,这种处理方法在热喷干扰研究中比较常见[10-11].

在计算中,该模型的输运系数计算方法与化学反应流一致:混合气体的输运系数采用Wilke 半经验公式计算,单个组分的输运系数采用气体动理论计算[25].该模型的状态方程及能量关系式同样与化学反应流一致,考虑了气体在高温下的热力学激发,包括各组分的束缚电子激发效应和分子组分振动能量激发效应[26].具体处理方法详见文献[17,19,27].

2.3 二元异质流模型

二元异质流模型中,将来流空气与RCS 喷流工质当作两种具有不同分子量和比热比的完全气体,流场介质可看作两组分量热完全气体混合物,它们之间无化学反应,但存在扩散现象.相比于化学反应冻结流,该模型的处理更加简化,因此计算效率更高,在热喷干扰研究中被广泛应用[7-9].

在该模型中,来流空气及喷流工质均采用了量热完全气体假设,输运系数采用Sutherland 公式计算,气体内能只是温度的线性关系式,即

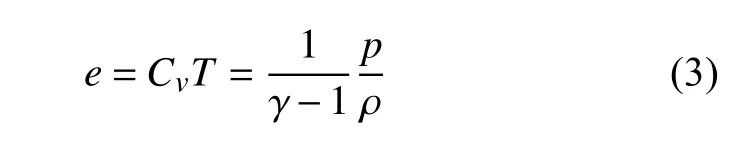
式中,e为气体内能,Cv为气体定容比热,T为气体温度,γ为气体比热比,p为压力,ρ为密度.本文中喷流工质比热比为1.27,来流空气为1.4.

2.4 空气喷流模型

由于在风洞试验中采用空气喷流重复性好、容易实现,因此有许多学者试图通过一些相似准则,以实现空气喷流对燃气喷流的替代模拟[12],这种模型同样采用量热完全气体假设,并且不需要考虑喷流和来流气体性质差异,因此可以极大提升计算效率.

本文采用与多数文献中相同的做法[12,28-29],即在空气、燃气喷流的喷管出口形状与面积保持一致的条件下,保证二者的压力比、动量比和质量流量比一致,如下

式中,p为静压,ρ 为密度,V为速度,下标j表示喷管出口参数,air 代表空气喷流,gas 代表燃气喷流.

3 计算方法的验证

这里采用文献[30]中的侧喷干扰风洞试验,来对本文的计算方法进行验证,计算外形如图1 所示,该外形由头部、身部和尾裙三部分组成,身部直径D=90 mm,长度为3.2D,头部长2.8D,尾部长3D,底部直径为1.66D,喷管出口直径4.6 mm,位于X/D=4.3 处.

图1 试验模型外形Fig.1 Configuration of the test model

该风洞试验包括冷喷和热喷两组状态,两组状态下的风洞来流均为空气,来流静压0.923 bar (1 bar=1 × 105Pa),来流静温105 K,来流马赫数3.0,攻角0°,喷流总压120 bar,喷流压比130.冷喷时喷流气体为空气,喷流总温293 K,喷流出口温度244 K;热喷时喷流气体为燃气,喷流总温2300 K,喷流出口温度2058 K,喷流出口比热比1.235,喷口处组分及质量分数为:CO2(38.21%),H2(1.73%),H2O(10.47%),CO(35.47%),N2(14.12%).

冷喷状态采用完全气体模型计算(比热比1.4),热喷状态采用前述的化学反应流模型计算.壁面处取绝热壁、无滑移、零压力梯度、非催化条件.

图2 给出了流场参数分布云图(其中流场对称面为Ma云图,模型表面为Cp云图),图3 给出了计算得到的模型表面压差系数分布与文献中冷喷试验数据的对比(ΔCP=CP,jet-CP,nojet),可以看出,本文的计算结果与试验数据吻合较好,计算结果准确地捕捉到了模型表面流向和周向的流动分离位置,对表面整个喷流干扰区域的压力系数分布预测也较为准确.

图2 流场参数分布云图Fig.2 Flow field parameters distribution contour

图3 模型表面表面压力系数分布对比Fig.3 Comparison of surface pressure coefficient distribution

4 计算结果与分析

4.1 研究对象及网格无关性验证

本文的研究对象为典型的锥柱裙外形,计算网格如图4 所示,该外形总长为2250 mm,身部直径386 mm,底部直径502 mm,RCS 系统喷管位于质心,距头部1177 mm.

图4 计算网格Fig.4 Sketch of computation grid

RCS 系统发动机为典型的小型火箭发动机,推进剂为N2O4/MMH,燃烧室总温3200 K,总压4 MPa,总推力为6800 N,喷管出口直径78 mm,喷管出口马赫数Ma=2.796,出口静压P=133.3 kPa,出口静温T=1596 K,出口燃气比热比y=1.27,气体常数R=400 J/(kg·K),组分质量分数见表2.

表2 喷管出口燃气组分质量分数Table 2 Hot gas species mass fraction at nozzle exit

为了验证网格收敛性,分别采用稀疏(网格高度5 μm,结果用coarse 表示),中等加密(网格高度1 μm,结果用medium 表示),加密网格(网格高度0.5 μm,结果用dense 表示)三套网格进行对比计算,计算状态为H=20 km,Ma=5,攻角a=0°的热喷干扰流场.表3 给出了气动力系数对比,其中CA为轴向力系数,CN为法向力系数,CMZ为俯仰力矩系数,图5 给出了喷口前方高热流区域的热流分布对比.可以看出,三套网格得到的气动力系数相差不大;稀疏网格得到的热流峰值偏低,加密网格与中等加密网格的热流分布差异较小,满足网格无关性要求,为了兼顾计算效率和精度,本文采用中等加密网格进行计算.

图5 不同网格得到的热流分布对比Fig.5 Comparison of heat flux

表3 不同网格计算得到的气动力系数对比Table 3 Comparison of aerodynamic characteristics computed by different grid

本文采用工程上常用的喷流干扰附加力、力矩以及放大因子来表征喷流控制效果.定义无喷时的气动力Fjetoff,力矩Mjetoff,喷流开启时的气动力Fjeton,力矩Mjeton,则喷流干扰附加力Fji、附加力矩Mji为

在本文条件下,喷流沿法向喷出,因此定义推力放大因子

由于本文选取的计算外形,喷管中心轴线位于飞行器质心位置,因此采用文献[31]中的方法定义力矩放大因子

式中,Fjet是喷管推力,D是弹体身部直径.

在本文计算中,气动力参考面积取飞行器最大截面积Sref=0.198 m2,参考长度lref=1.0 m,力矩参考点为质心位置Xref=1.177 m,Yref=0.0 m,Zref=0.0 m,俯仰力矩以抬头为正.

4.2 气体模型对热喷干扰流场的影响

这里首先采用前述的化学反应流(reacting)、反应冻结流(froz)、二元异质流(binary)以及空气喷流(air)模型对本文第3 节中的热喷试验状态进行了数值模拟,并与试验数据进行了对比.

图6 给出了计算得到的模型表面压差系数分布与文献中热喷试验数据的对比,可见,化学反应流得到的表面压力分布与试验数据吻合较好,其余三种模型预测的分离区范围均明显小于试验数据.这说明在该试验条件下,为了反映真实物理环境,有必要更加全面地考虑干扰流场中的详细化学反应机制,采用化学反应流模型进行计算.

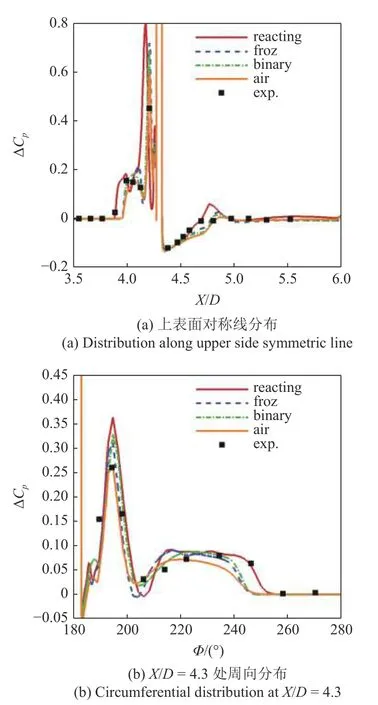
图6 模型表面压力系数分布对比Fig.6 Comparison of surface pressure coefficient distribution

为了进一步分析气体模型对热喷干扰流场数值模拟的影响,这里针对前述的锥柱裙外形,选取H=20 km,Ma=5,a=0°状态,开展了不同气体模型的对比分析.在计算中,采用k-ωSST 湍流模型,对壁面处取等温壁300 K、无滑移、非催化、零压力梯度条件,喷口处取为喷管出口条件(表3).

表4 给出了不同模型得到的飞行器表面气动力结果对比.从表中可以看出,在该计算状态下,不同计算模型得到的轴向力系数差别较小,最大差别在1.3%以内,但不同模型得到的喷流附加推力和附加力矩差异较大,从而导致法向力系数和俯仰力矩系数差异较大.具体来看,当前计算状态下的喷流干扰效应会产生向下的喷流附加推力以及附加低头力矩,与化学反应流的结果相比,其余三种模型的附加推力明显更小,附加力矩明显更大,下面将分析产生这种现象的原因.

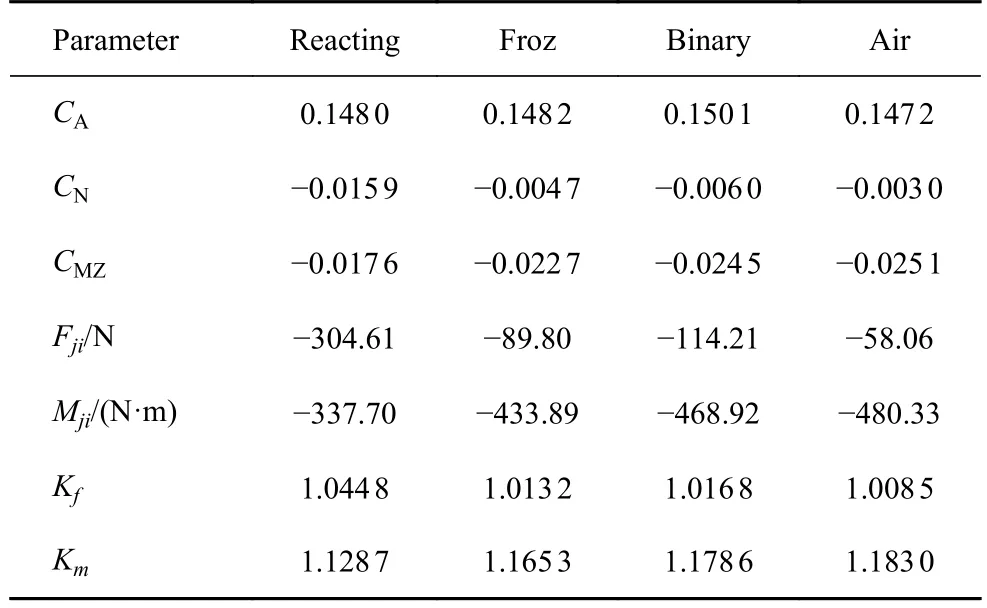
表4 不同计算模型得到的气动力特性对比Table 4 Comparison of aerodynamic characteristics by different gas model

图7 给出了飞行器表面不同位置的压力分布对比,从图中可以看出,化学反应流相比于其他三种模型,得到的表面喷流干扰区范围增大,同时干扰区内压力明显升高,这是由于喷流燃气中含有未反应完全的CO 和H2等组分,其进入主流后会与来流发生二次燃烧反应,如图8 所示,在喷口附近区域,流场中的O2组分质量分数下降,CO2和H2O 组分质量分数升高,而CO2和H2O 正是二次燃烧反应的主要产物,由于这些反应均为放热反应,其释放的化学能使得喷流气体进一步膨胀,进而导致喷流干扰区范围变大,干扰区压力升高.

表5 给出了飞行器的局部区域气动力系数对比,表中下标up 表示弹体上表面的气动力积分结果,下标down 表示下表面,upstream 表示喷口上游部分的气动力积分结果,downstream 表示喷口下游部分.结合图7 可知,化学反应流得到的喷流干扰区范围变大,干扰区压力升高,由于喷流干扰区主要位于弹体上表面,从而导致弹体上表面的气动力积分结果CN,up绝对值增大,同时,由于喷流干扰效应对下表面压力分布影响较小,各气体模型得到的下表面积分结果CN,down相差不大,因此,整体的积分效果表现为化学反应流的法向力系数CN绝对值增大,喷流附加推力增大.从表5 还可以看出,喷口上下游部分的积分效果均表现为低头力矩,但由于喷流干扰区大部分位于喷口下游,因此力矩主要由下游部分贡献,从图8(a)和8(b)可知,喷口下游上表面对称线附近存在较强的二次燃烧反应,导致这一区域压力明显升高(如图7(b)所示),这一部分的压力积分表现为一个抬头力矩,因此化学反应流得到的CMZ,downstream绝对值明显偏小,从而导致其附加低头力矩明显偏小.

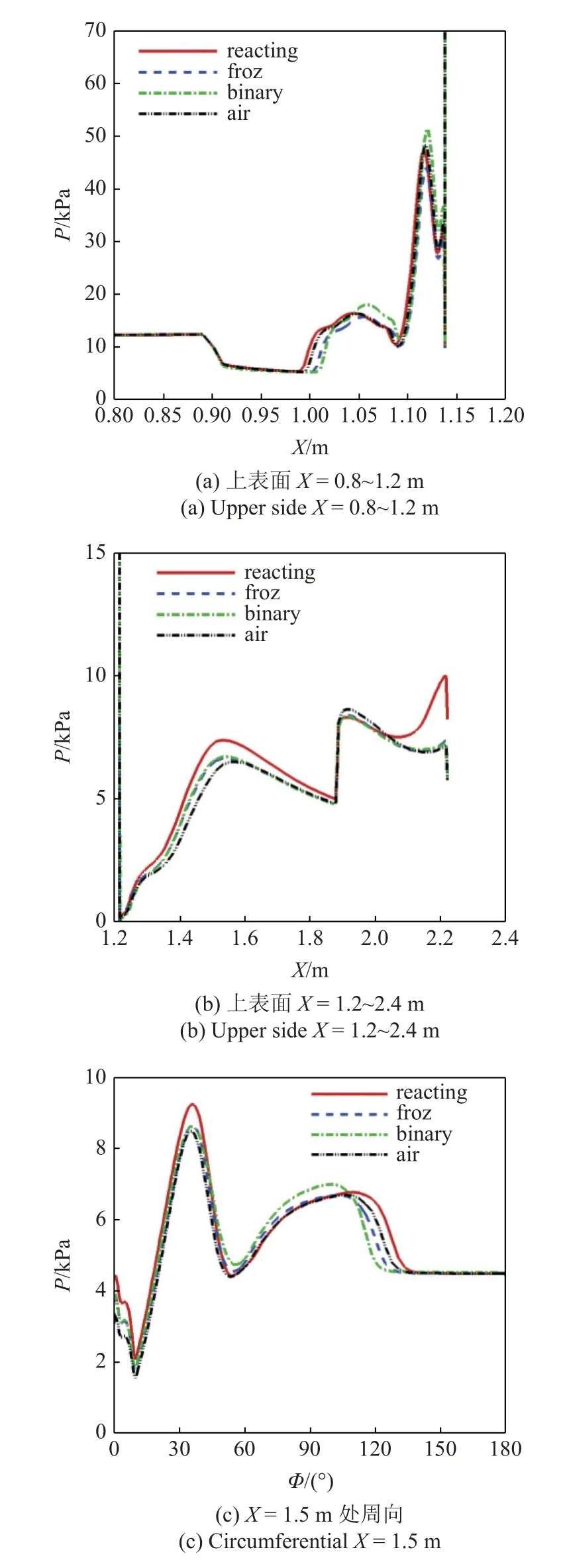
图7 表面压力分布对比Fig.7 Comparison of surface pressure distribution

图8 喷口附近的组分质量分数分布对比Fig.8 Species mass fraction distribution near nozzle outlet

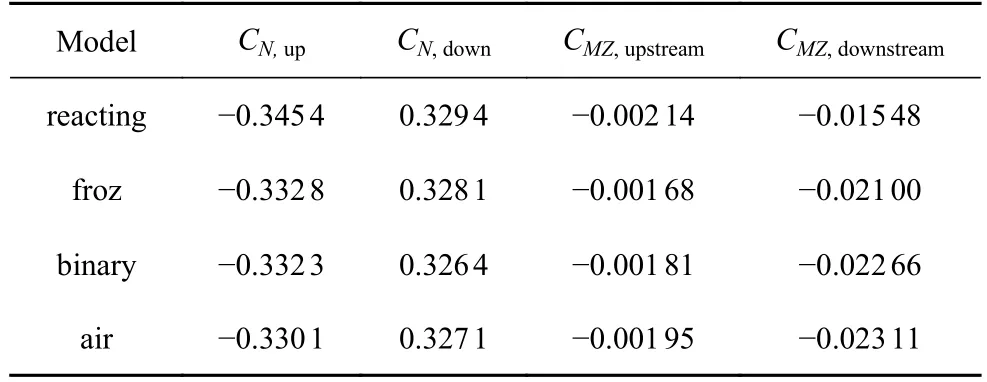
表5 飞行器局部区域气动力系数对比Table 5 Comparison of part aerodynamic coefficient

从表4 和图7 还可以看出,三种简化模型之间的表面压力分布和气动力特性差异相对较小,说明在当前计算状态下,气体热力学激发和喷流工质比热比差别的影响相对较小.

图9 给出了上表面对称线上的热流分布对比,可见三种简化模型得到的热流峰值差异不大,但与化学反应流的结果相比,其热流峰值低约22%,结合图8 可知,该区域是生成CO2和H2O 反应较剧烈的区域,二次燃烧反应释放的化学能造成了该区域表面热流升高,这也说明若采用简化模型进行计算,将低估飞行器表面的热流值,对防热系统设计不利.

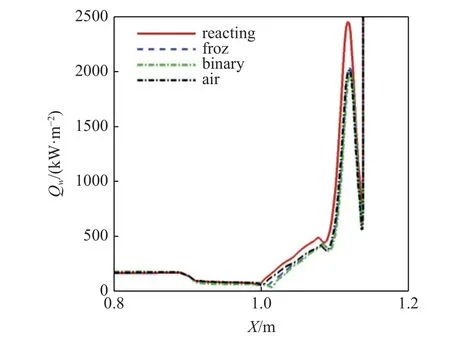
图9 上表面对称线上热流分布对比Fig.9 Comparison of heat flux distribution along upper side symmetric line

图10 给出了不同气体模型的残差收敛曲线和CPU 计算时间对比,综合来看,采用空气喷流模型的计算效率明显最高,二元异质流次之,而由于采用了多组分气体描述喷流燃气,化学反应流和反应冻结流不仅收敛较慢、在同样步数下的CPU 计算时间明显更长,计算效率较低.

图10 不同气体模型的计算效率对比Fig.10 Comparison of efficiency for different model

总的来看,在当前计算条件下,采用简化模型进行热喷干扰流场的数值模拟时,飞行器的气动力热特性预测将出现一定偏差;若采用更加复杂的化学反应流模型进行计算,其计算效率较低.

更进一步来看,当飞行条件变化时,流场中化学反应和热力学激发等物理化学现象的剧烈程度也会发生改变,在一些条件下,采用合适的气体模型可以实现计算效率和精度的兼顾.因此,本文接下来将开展不同飞行条件下气体模型对热喷干扰流场数值模拟的影响分析.

图11 给出了高度H=20 km,攻角a=0°,马赫数Ma=4～ 10 状态下的气动力热特性对比.可见,随着马赫数增大,化学反应流与简化模型得到的结果差异逐渐增大,同时,在高马赫数条件下,三种简化模型相互之间的差异也明显增大.以下从三个方面分析其原因:(1)随着飞行马赫数增大,来流的氧气质量流量增大,使得二次燃烧反应更加充分,同时,高马赫数下喷流与来流相互干扰作用更强,类似于激波诱导燃烧,在更强的激波作用影响下会诱导发生更强的二次燃烧反应,因此化学反应流与简化模型得到的结果差异逐渐增大;(2)随着马赫数增大,喷流与来流相互干扰作用增强,造成喷流干扰区内温度升高(如图12 所示),由于冻结流考虑了多组分气体内能各个模态的激发,在高温状态下,将更加偏离完全气体状态,此时虽然喷口处燃气比热比是一致的,但相比于低马赫数状态,高马赫数下整个干扰区内气体比热比出现了明显变化(如图13 所示),而这将导致气体热力学特性发生变化,从而导致冻结流与二元异质流的差异增大;(3)在高温条件下,由喷流工质的比热比差别所导致的气体膨胀特性差异将会更加明显,因此二元异质流与空气喷流的差异随着飞行马赫数增大而增大.

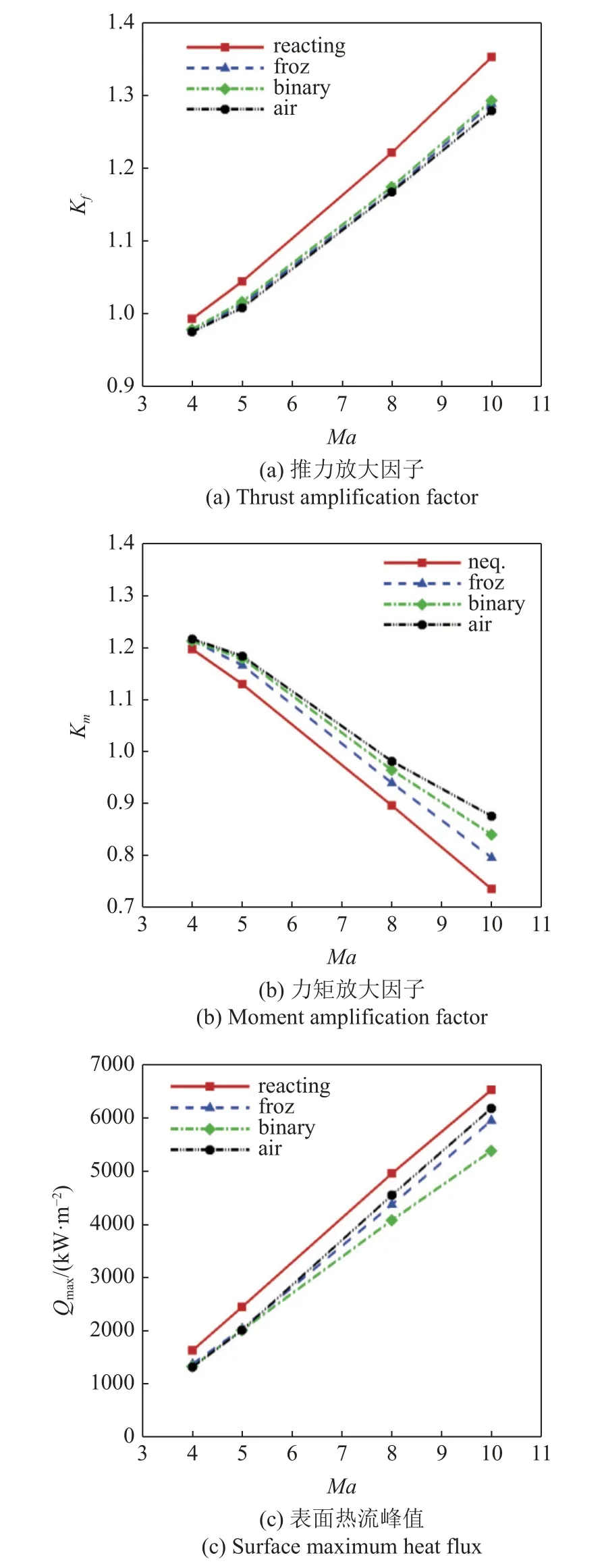
图11 不同马赫数下的气动力热特性对比(H=20 km,a=0°)Fig.11 Comparison of aerodynamic and aerothermal characteristics for different flight Mach number (H=20 km,a=0°)

图12 反应冻结流温度云图对比(H=20 km,a=0°)Fig.12 Comparison of specific heat ratio contour for chemical frozen flow (H=20 km,a=0°)

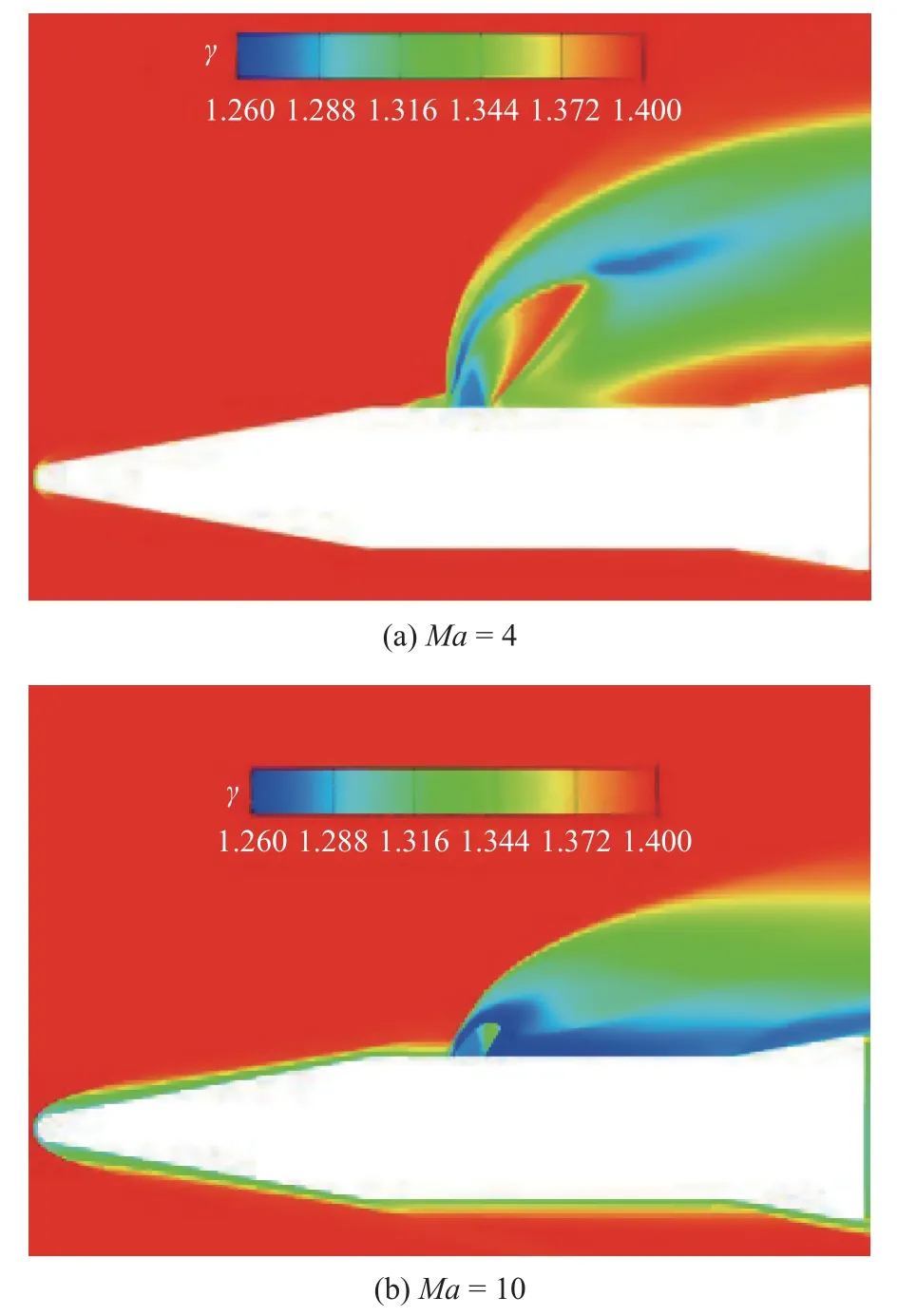
图13 反应冻结流比热比云图对比(H=20 km,a=0°)Fig.13 Comparison of specific heat ratio contour for chemical frozen flow (H=20 km,a=0°)

总的来看,随着飞行马赫数增加,简化模型对热喷干扰气动力热特性预估的误差增大,同时不同简化模型之间的差异也将增大,此时有必要更加全面地考虑问题的物理本质,采用化学反应流模型进行计算.

图14 给出了高度H=20～ 50 km,马赫数Ma=5,攻角0°状态下的气动力热特性对比.可见,随着飞行高度增加,化学反应流与简化模型之间的差异迅速减小,在高度30 km 以上时,不同计算模型得到的飞行器气动力热特性差别已经较小.下面分析其原因:随着飞行高度增加,来流密度迅速降低(从高度20 km 到50 km,来流密度下降了两个量级),因此来流氧气质量流量迅速降低,当来流氧气质量流量过低时,由于缺乏氧化物,流场中二次燃烧反应将明显减弱,因此化学反应流与简化模型的差异明显减小;同时,高空条件下,喷流与来流相互干扰作用将会减弱,喷流干扰区内温度降低,此时气体内能模态激发以及喷流工质比热比差别的影响将减小,因此三种简化模型相互之间的差别进一步减小.

图14 不同高度下的气动力热特性对比(Ma=5,a=0°)Fig.14 Comparison of aerodynamic and aerothermal characteristics for different flight altitude (Ma=5,a=0°)

图15 给出了高度H=20～ 50 km,马赫数Ma=10,攻角0°状态下的气动力热特性对比.可见,即使在较高马赫数条件下,随着高度增加,气体模型的影响同样迅速减小,说明此时飞行高度仍然是主要影响因素,类似地,在30 km 以上时,不同计算模型得到的飞行器气动力热特性差别已经较小.需要补充说明的是在Ma=10 状态下,由于飞行速度很高、喷流干扰作用很强,在低高度条件下俯仰力矩出现了反向的现象(由低头变为抬头),因此图15(b)中的变化趋势与图14(b)有所不同.

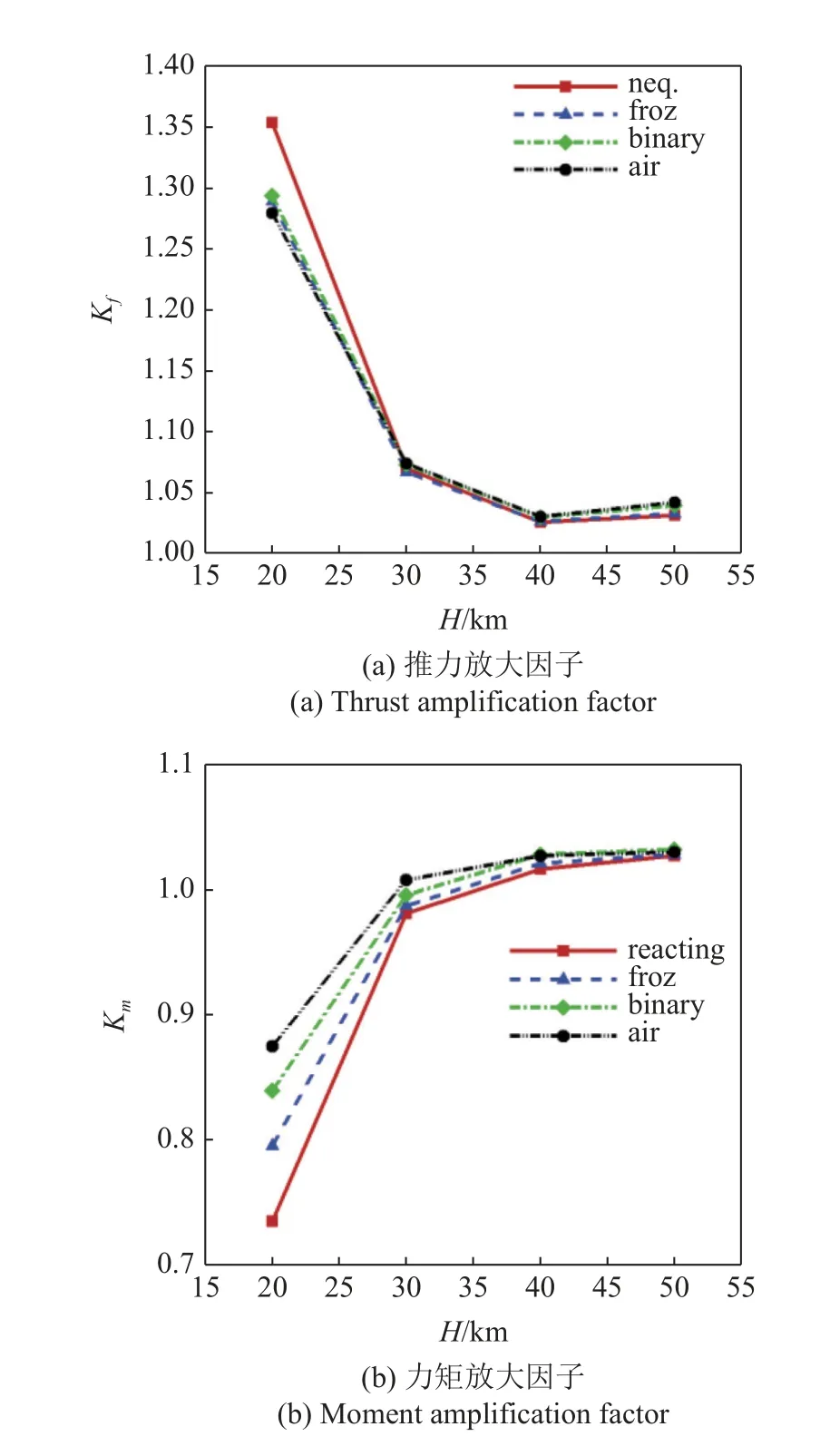
图15 不同高度下的气动力热特性对比(Ma=10,a=0°)Fig.15 Comparison of aerodynamic and aerothermal characteristics for different flight altitude (Ma=10,a=0°)

总的来看,简化模型对飞行器热喷干扰气动力热特性预估的偏差,在低飞行高度状态下较明显,当飞行高度较高时,这种偏差明显减小,此时可以采用简化模型进行计算,在提高计算效率的同时也可以保持较高的预测精度.

5 结论

本文针对锥柱裙外形,分别采用化学反应流、反应冻结流、二元异质流以及空气喷流四种气体模型开展了RCS 热喷干扰流场的数值模拟,开展了不同气体模型对热喷干扰流场结构、飞行器气动力热特性的影响特性和规律研究,得到以下结论.

(1)从与风洞试验数据的对比来看,化学反应流模型与试验数据的吻合程度优于三种简化模型,要准确反映热喷干扰流场特性,应尽量采用化学反应流模型进行计算.

(2)在本文条件下(高度H=20～ 50 km,Ma=4～10),飞行高度较低时(约30 km 以下),采用简化模型进行热喷干扰流场数值模拟,会低估分离区大小,使飞行器气动力特性预测出现偏差,同时也会低估表面热环境,对防热系统设计不利;随着马赫数增加,这种偏差将会进一步增大,同时不同简化模型之间的结果差异也进一步增大.

(3)飞行高度较高时(约30 km 以上),简化模型对飞行器热喷干扰气动力热特性预估的偏差明显减小,此时可采用简化模型进行计算,在保证精度的同时大幅提升计算效率.

本文选取的外形和计算状态仍相对有限,在更高飞行高度及更高马赫数状态下,流场中会进一步出现离解/电离效应、热化学非平衡效应、稀薄滑移效应等复杂的物理化学现象,因此在后续的研究中,有必要进一步探索多种外形、多种飞行状态下热喷干扰效应对飞行器气动特性的影响特征及规律.