混合课程学生成绩预测模型的可解释性探究*
□ 罗杨洋 韩锡斌
一、引言
近年来,人工智能技术与教育教学融合应用受到各方关注。已有许多研究在实验环境中提出智能评价方案、智能学习模型、智能教学决策推荐方法,然而真正应用到实践并为教育教学带来变革的智能技术还很少(韩锡斌,等,2017;赵帅,等,2019)。产生这种现象的原因包括技术壁垒、开发成本、模型和结果的解释困难等(刘三女牙,等,2019;孟翀,等,2021;肖睿,等,2020)。人工智能为教育提供服务的核心是机器学习算法构建的各种模型(蒋鑫,等,2020)。机器学习构建模型的可解释性是教学实践者信任人工智能服务的前提(孙众,等,2021),然而通过机器学习算法构建的模型包含着不确定性,构建模型的过程不透明,大多数结果与教育教学规律关联薄弱,导致教学实践者难以信任这些模型(Niels,2020)。在机器学习构建的众多模型之中,学习成绩预测模型最受关注,它可以支持师生动态调整教学策略,提供变更学习路径的有效方法,切实优化教育教学。探究学习成绩预测模型的可解释性有助于揭示不同场景下的学习规律,帮助教师理解不同学生的学习经历、信任预测结果并依此为学生提供个性化帮助(郑勤华,等,2019)。本研究旨在分析近年来学习分析领域和计算机科学领域对预测模型的可解释性研究,利用计算机科学领域解释预测模型的研究基础,以混合课程场景下基于学生在线行为的成绩预测模型为例,分析成绩预测模型结构所代表的教育意义,其内在推理机制所揭示的学习行为与学习成绩之间的预测关系,以及预测结果为教学实践提供的启示,对教师应用成绩预测模型提出建议。希望本研究有助于教学实践者理解、应用成绩预测模型,为研究者提供解释混合课程场景中成绩预测模型的研究思路和分析框架。
二、研究现状与问题
当前学界对机器学习的可解释性还没有统一的界定。Miller(2017)指出,可解释性是指人类理解机器学习做出决策原因的程度。Lipton(2018)将可解释性定义为人类使用机器学习模型从数据中揭示出知识时所揭示的知识彼此之间的关联性。陈珂锐等(2020)认为机器学习的可解释性即使用可理解的术语表达机器学习过程和结果中所包含的概念。在教育领域,多个研究将可解释性概括为参与教学的人在以下三个方面对预测模型的理解程度:知晓模型收集数据的目标,理解模型处理数据的过程,应用模型预测的结果(Xing,et al.,2015;Zhang,et al.,2019;Jeon,et al.,2019)。正如Villagrá-Arnedo等人(2017)所指出的,提升预测模型的可解释性是一个将“黑箱”透明化的过程,需要在数据解释、过程解释和预测结果解释等多方面做出努力。探索学习成绩预测模型可解释性的研究主要涉及学习分析和计算机科学两个领域。
(一)学习分析领域内的预测模型可解释性研究
学习分析领域内的学者尝试过多种解释机器学习模型及其结果的方法。如Xing等(2015)解释了基于决策树预测完全在线学习中学生成绩的过程和结果,该研究将学生在网络教学平台中的学习过程视为一种活动,依据活动理论(activity theory)构建学习过程数据与学习成绩的联系,选择遗传算法调参后的各种决策树算法构建学习成绩预测模型,根据遗传算法确定的参数和决策树的结构解释了学习过程数据和学习成绩结果之间的预测规则。Sorour等人(2016)为了构建可解释的学习成绩预测模型,同样使用了树状结构的算法。该研究将学生的行为标签化,使用学习行为—标签属性—情境的规则,解释了随机森林算法将学生的学习过程数据转化为预测结果的过程和路径。Zhang等人(2019)同样采用了遗传算法构建学习成绩预测模型,并使用树状结构的预测变量与结果变量规则解释整个预测过程,说明了在研究情境下预测学习成绩需要的重要变量以及这些变量之间的关联。树状结构的预测模型还可转化为“if……then……”条件判断语句,该表达方式也有利于教师将预测模型中提供的信息转化为教学策略或教学干预。
基于决策树算法构建的预测模型只是成绩预测模型中的一小部分。随着学习情境的复杂化,许多研究都使用了多层神经网络的深度学习模型以提升预测结果精度,但为成绩预测模型的可解释性带来了更大挑战 (胡航,等,2019)。Villagrá-Arnedo等人(2017)指出,在解释“黑箱”算法构建的预测模型时,解构模型的结构、描述预测模型内在推理机制揭示的预测关系,以及解释预测结果对教学实践的启示是有效手段。Donda等人(2020)通过特征工程、算法比较和预测过程的时序分析,应用了Villagrá-Arnedo等人(2017)提出的成绩预测模型的解释框架。
(二)计算机科学领域内的预测模型可解释性研究
预测模型早期的可解释性主要通过事前的数据分布假设和建模时人工限制模型的复杂性来保证(Lei,et al.,2018)。然而,随着机器学习模型逐渐非线性化和非参数化,模型的可解释性逐渐降低。有学者指出,相较于整合树(tree ensemble)模型或深度神经网络模型,回归模型和关联规则模型的可解释性更强(王亮,2021;Zeileis,et al.,2008)。随着应用场景的复杂化,对预测精确性的要求不断提高,解释非参数、非线性的复杂机器学习模型成为学界和社会关注的焦点。
当前计算机科学领域中的模型可解释性研究大多围绕解释框架研究和解释技术研究两个方面展开。
解释框架是解释特定模型时必须解释的内容。预测模型的解释框架由以下三部分构成:预测模型结构的解释,预测模型内在推理机制的解释,以及预测结果的解释(Murdoch,et al.,2019)。其中,预测模型结构的解释是说明预测模型的构成要素及要素之间的关系;预测模型内在推理机制的解释是说明数据输入预测模型后会经由何种处理方法转变为何种形态,对预测结果产生的影响是什么;预测结果的解释包括预测结果与预测变量之间的关系解释和预测结果在特定场景中表达的意义等(Molnar,2019)。
解释技术是指分析、诊断和可视化机器学习过程的技术和方法(Vidovic,2017,p.18)。这些技术和方法对应解释框架的每个方面。如在解释模型组成方面,有研究采用特征工程(feature engineering)技术提取输入变量的意义,结合模型的数学基础描绘模型可能形成的结构(Montavon,et al.,2018);在解释预测模型内在推理机制方面,有学者(Cherkassky,et al.,2015)建议根据预测模型处理数据的方法,采用抽象的理论模型替代具体的预测模型;在预测结果的解释方面,有针对特定场景的结果可视化技术将数字和概率转换为更形象的图形(Hall,et al.,2018,pp.14-27)。
综上所述,当前学习分析领域内解释预测模型的框架和技术均借鉴计算机科学领域对预测模型的可解释性研究。在成绩预测模型的解释研究中,学界倾向于回归教学场景,以计算机科学领域的方法为基础,结合学习分析领域的实践,形成了包含分析预测模型的结构、解释内在推理机制和提出预测结果的应用建议这三部分内容的解释框架,也为本研究解释预测模型提供了基础。然而,这些研究还局限在完全在线课程场景中,大多基于决策树算法,只解释了准确率较高的结果,忽略了对预测错误产生原因的解释,也缺乏对学生整体预测结果和个体预测结果之间存在差异这一现象的解释。
混合课程是结合在线与面授两种教学场景授课的课程,且其中有较大比例的教学是通过在线授课实现的(韩锡斌,等,2016,pp.320-323)。有关混合课程中学生成绩预测的研究大多采用学生线上学习过程数据来构建预测模型。在缺失学生线下学习过程数据的情况下,依赖不完整的学习过程数据构建的学生成绩预测模型与完全在线课程中学生成绩预测模型在解释性上有较大差异,当前尚缺乏解释此类成绩预测模型的研究。
基于上述文献分析,本研究提出两个问题:
问题1:如何解释混合课程中学生成绩预测模型?
问题2:在混合课程中构建学生成绩预测模型能为教师提供哪些帮助?
三、研究方法和结果
(一)混合课程数据收集和预处理
依据数据可获得性和研究可行性,以往研究均推荐采用学生在网络教学平台中的学习日志构建混合课程中学生成绩预测模型(Hellas,et al.,2018;Conijn,et al.,2018)。选择一所学校一学期的学生网络教学平台学习日志,将学生对网络教学平台的操作与学习活动对应,依据Moore(1989)提出的教学交互对象划分和陈丽(2004)提出的交互活动类型划分理论,尽量收集囊括所有交互对象和交互类型的教学活动,并依据以往研究中使用过的学生在线行为指标,从学生在线学习日志中提取学生在线学习活动指标作为预测变量(predictor variable,PV)。采用最大值—最小值归一化方法处理混合课程中的学生在线行为数据,去除数据量纲;从学校教务系统中提取每门课程的学生成绩,以学校的学分绩转换方式将百分制的学生成绩转化为A(100~90)、B(89~80)、C(79~70)、D(69~60)、F(60分以下)五等。去除学生学分绩完全相同的课程数据,获得本研究所需结果变量(outcome variable,OV)(见表1)。
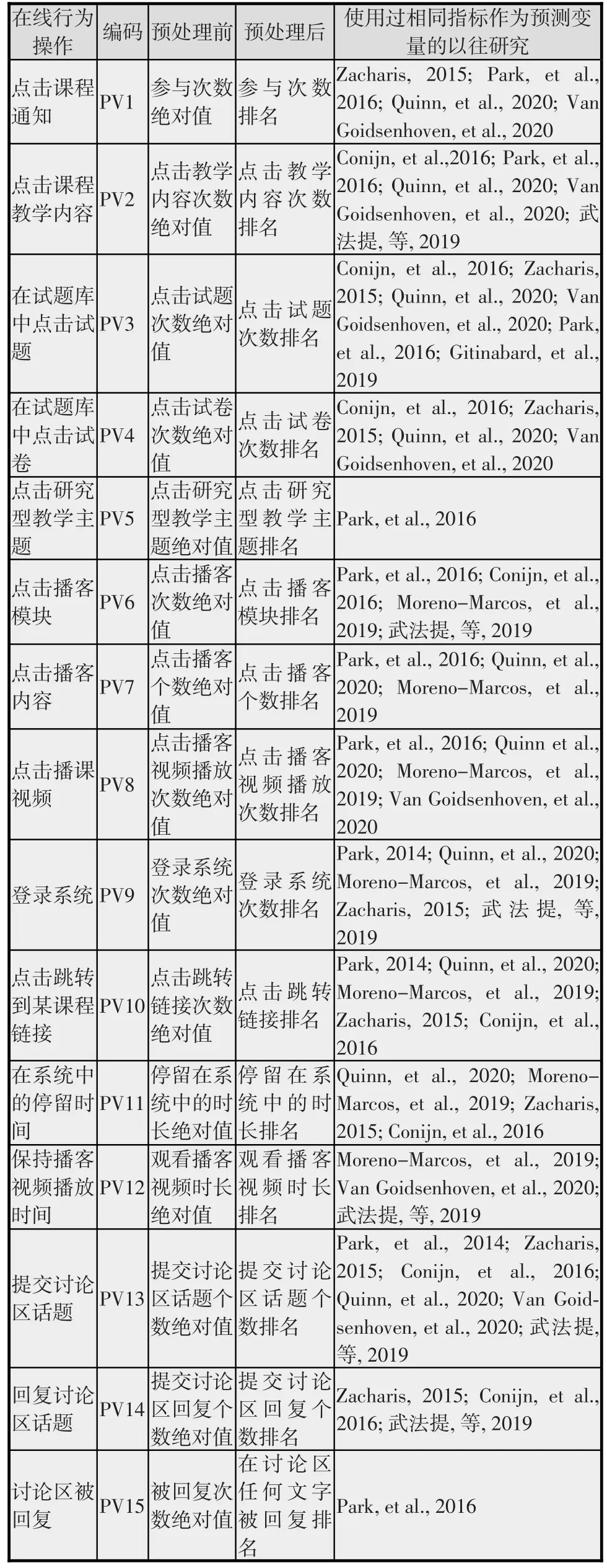
表1 学生成绩预测模型输入变量表
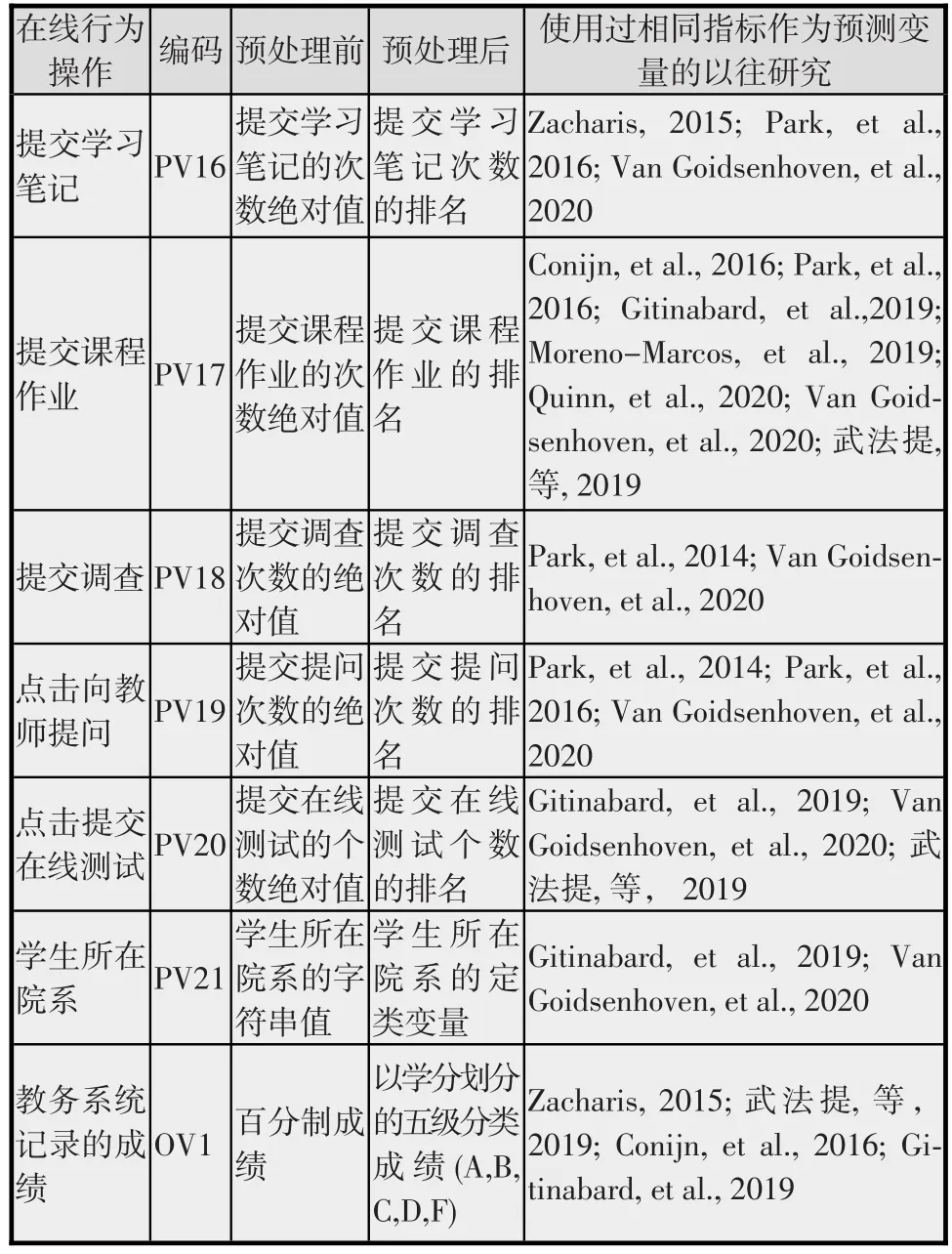
续表
采用本团队以往提出的混合课程分类方法(Luo,et al.,2020),选择学生在线行为活跃度较高的混合课程(共22门,2,348名学生),这类课程来自于生命科学、电气与电子工程、法学、计算机科学和外语五个专业,每门课程学生数量差异小于20人,均采用线上线下混合教学。参与该类课程的学习者为攻读本科学位的学生,在参与课程方面的典型特征是:整体在线行为活跃度较高,几乎全面参与各类交互学习活动;在各种在线行为指标上有较大个性化差异;学生成绩分布与全校学生成绩分布相似。
(二)解析混合课程的学生学习成绩模型
使用当前研究中常见的五种机器学习算法构建学习成绩预测模型,分别是逻辑回归、多层感知器、随机森林、多核支持向量机和朴素贝叶斯。在构建学习成绩预测模型的过程中,记录算法输出的中间结果作为解释模型的依据。步骤如下:
首先,将混合课程数据分为11份,其中10份作为开发集,1份作为测试集。
其次,在开发集中采用上述五种算法分别构建预测模型,在构建模型时采用超参数调试法优化算法参数。采用10折交叉验证分析预测模型,在交叉验证中将开发集划分为1份验证集和9份训练集,并进行迭代验证。输出构建预测模型的中间结果。
再次,将测试集输入预测模型中,比较预测结果的差异。
最后,依据中间结果、预测结果和混合课程的场景,解释不同算法所构建的预测模型结构所代表的教育意义,其内在推理机制所解释的学习行为对成绩的预测关系,以及预测结果对实施混合课程带来的启示。
研究流程如图1所示。

图1 成绩预测模型可解释性研究流程图
(三)混合课程学生学习成绩预测模型的比较
在本研究中混合课程学生成绩是一个五级定类变量,且混合课程中的学生数量在各成绩等级中具有较大差异,属于非平衡数据的多分类问题。通常评价多分类问题的指标包括权重准确率(weighted accuracy)、权重查全率(weighted recall)和权重F1值(weighted F1 measure)评价。这些指标从二分类预测结果评价公式推理得出,指标的值会受到不同分类数量的影响(Hossin,et al.,2015)。为综合评价各预测算法构建的模型及其预测结果,研究在上述指标基础上加入了平均准确率(average accuracy)、平均查全率(average recall)和宏F1值(Macro-F1 measure)等适用于非平衡数据的多分类问题评价的指标(Shmueli,2020),从而更准确地描述每个等级成绩的预测结果,为优化教学实践提供更有意义的数据。根据各预测模型的测试数据和交叉验证的评价结果(见表2)可知,以随机森林算法构建的预测模型不但具有较高的预测结果准确率,而且在查准率和查全率等指标中都有较好表现。
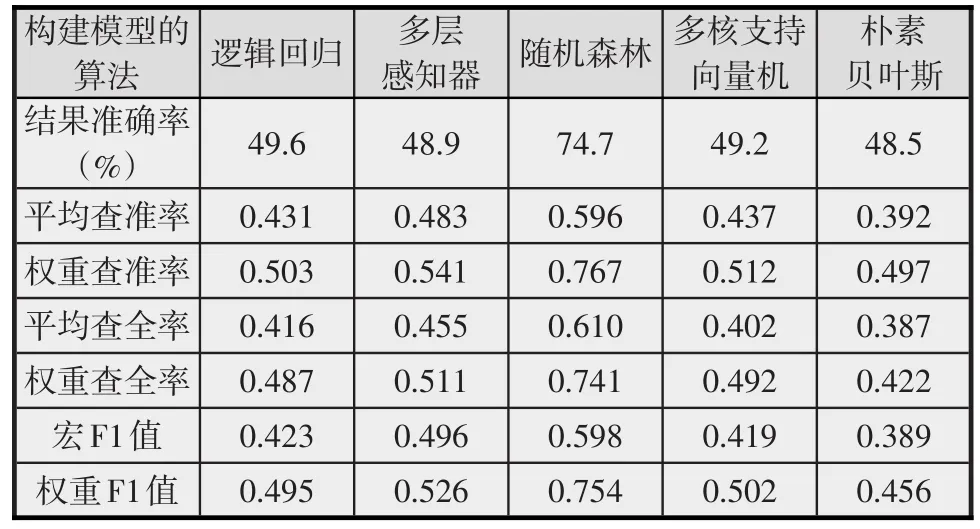
表2 各模型预测结果评价指标
四、结果讨论
(一)以机器学习算法构建的成绩预测模型结构所代表的教育意义
机器学习算法在数学原理上的差异导致以这些算法构建的成绩预测模型在结构上代表了不同的教育含义。
在本研究中,逻辑回归算法找出在混合课程中预测学生学习成绩最准确的在线学习行为指标及其权重。在该预测模型中,不同于单门混合课程,在多门混合课程场景下,这种结构表示了每种学生成绩等级下大多数学生的学习行为模式(Donda,et al.,2020),这些行为模式可能跨课程出现。该预测模型通过发现大多数学生在线学习行为与学习成绩的关联关系中最显著的那对关联关系,给出对最终成绩影响最大的在线学习行为指标及其权重。该模型可帮助教师在学习结束时点预测每位学生的学习成绩(Balle,etal.,2018)。
多层感知器算法关注的是学生的在线学习行为与其成绩等级在对应上的误差及修正该误差的指标及其权重,因此整个预测模型表示的是学生的在线学习行为指标与其成绩等级之间的唯一映射关系。在多门混合课程场景中,学生在线学习行为指标中预测每个成绩等级最准确的指标被选出,表示各混合课程中影响学生获得每类最终成绩的共通性在线学习活动。该模型可帮助教师在任意学习时点预测每位学生的成绩。
随机森林算法构建的是多种学生在线学习行为指标模式对学习成绩的预测关系。在该模型中,在线学习行为指标的值会被划分为不同的区间,形成多种在线学习行为指标序列对应的一类学习成绩(方匡南,等,2011)。这种结构说明,当只采用在线学习行为预测学习成绩时,在不同的混合课程中可用于预测学习成绩的最显著的在线学习行为模式有多种。该模型可帮助教师在任意学习时点预测每位学生在不同课程中的成绩。
多核支持向量机构建的是所有学生在线学习行为指标对应每类学习成绩的关系模型,该模型表示的是在不同混合课程中,以学生在线学习行为预测五类学习成绩的结果(刘方园,等,2018)。该模型可帮助教师在任意学习时点预测每位学生的学习成绩,但该模型无法区分不同课程中学生在线学习行为预测学习成绩的差异。
朴素贝叶斯算法关注的是当学生的在线学习行为达到某种条件时所对应的学习成绩,因此该模型表示的是在混合课程学习结束时点达成某种值的在线学习行为所得到的学习成绩。该模型能帮助教师在学习结束时点只观察几项在线学习行为就可以预测学生的学习成绩。
(二)不同成绩预测模型内在推理机制揭示的预测关系
从逻辑回归模型结构代表的教育意义讨论可知,逻辑回归模型预测的推理机制是,寻找新学生与模型最匹配的在线学习行为模式所对应的学习成绩。但在本研究的混合课程场景下,学生的学习过程包含线上和线下两部分,仅使用在线学习过程数据预测学习成绩可能出现两种逻辑回归无法区分的情况:一是学生的在线学习行为数据相似而学习成绩不同;二是学生的在线学习行为数据不同而学习成绩相似。因此,逻辑回归模型的预测结果无法区分学生参与不同混合课程时的在线学习行为差异,由表2可知该模型预测效果较差。
多层感知器预测的推理机制是通过比较所预测的学生成绩与学生实际成绩之间的差异来不断修正学生在线学习行为指标的权重(Dreyfus,et al.,1990),并计算新加入学生的在线学习行为所对应的学习成绩。在本研究中,存在相同学生参与多门混合课程的情况,在不同要求下学生的在线学习行为与学习成绩之间的关联存在多种对应关系,因此预测结果准确率较差。例如,当神经网络模型学习一门课程中成绩为A的学生的在线学习行为数据时,其他成绩等级学生的在线学习行为都会被认为是非A的数据,而当该学生在其他课程中成绩为非A,但其在线学习行为数据与本课程相似时,模型对该学生在线学习行为模式的识别就会出现二义性。在混合课程中,在线学习行为只代表学生的部分学习参与,与学习成绩的关联也存在多重对应关系,因此如表2所示,多层感知器模型会出现较多预测错误。
随机森林模型预测的推理机制是,依据混合课程中不同学生群体的在线学习行为与学习成绩之间的预测关系对新加入的学生进行划分,在此机制下模型可识别某类成绩等级下的多种学生在线学习行为模式,切割由于学生成绩跨等级而在线学习行为模式又相似所产生的交互影响。例如,当某位成绩为A的学生的在线学习行为与其他成绩分类的学生相似时,模型会寻找该学生所属的群体,并使用投票的方式预测该学生的成绩。虽然在混合课程中在线学习行为只是部分学习行为,但每类成绩的学生其行为模式不会过于分散,通过每门课程中大多数学生的在线学习行为即可分辨新加入学生的成绩。只有某门课程中学生的学习成绩与在线学习行为都十分相似时,随机森林模型的推理才会出现错误。例如,成绩为A的学生与成绩为F的学生其在线学习行为数据相近,同时该课程中学习成绩分别为B、C、D的学生中有相近行为的学生数量也较多,但这种情况不符合混合教学规律。由表2可以看出,该模型的预测结果各项指标较高。
多核支持向量机模型预测的推理机制是,判断新加入学生的在线学习行为数据与模型中在线学习行为数据的一致性,从而获得对该学生成绩的预测。在该模型构建过程中不同批次输入的数据所产生的错误会逐步累积,即当某门课程中存在将F成绩的学生识别为A成绩的学生时,其他课程中与错误识别学生相关的在线学习行为都将被识别为A成绩。另外,支持向量机会发生“拒绝分类”错误(Arun,et al.,2011)。在本研究中,每个成绩等级下的学生数量不同,各混合课程中学生成绩等级对应的学生在线学习行为模式也有差异。在某门课程中建立的各成绩等级与在线学习行为的对应关系错误会随着迭代而累积,导致最后在预测时出现巨大偏差。同时,各成绩等级内部在预测时出现“拒绝分类”后,被拒绝的学生会被划分到最接近的成绩等级中。这种划分方法对学生在线学习行为模式接近但成绩等级有差异的样本会产生大量错误的分类,因此在表2中该模型预测结果的各项指标较差。
朴素贝叶斯模型预测的推理机制是,根据模型所得条件概率计算学生在线学习行为属于每一等级学习成绩的概率,并将概率最高的学习成绩作为预测结果。与逻辑回归相似,这种预测方法难以识别相同的学生在线学习行为数据(相同条件)对应不同成绩等级(不同结果)时发生的错误。从表2可知,朴素贝叶斯模型在本研究中也无法获得较好的预测结果。
(三)预测结果的解释及其对教学实践的启示
根据表2,本研究中预测准确率较高的混合课程学生成绩预测模型是随机森林预测模型。图2展示了随机森林模型预测某位学生成绩为A的流程,其中PVn代表学生在线学习行为各指标数据(预测变量),OV(N)代表输出的学生成绩等级(预测结果),xn代表决策树叶子节点进行下一步判断的学生在线学习行为数据阈值(依据变量),该变量根据训练过程中学生在线学习行为对学习成绩的信息量贡献不断优化获得。
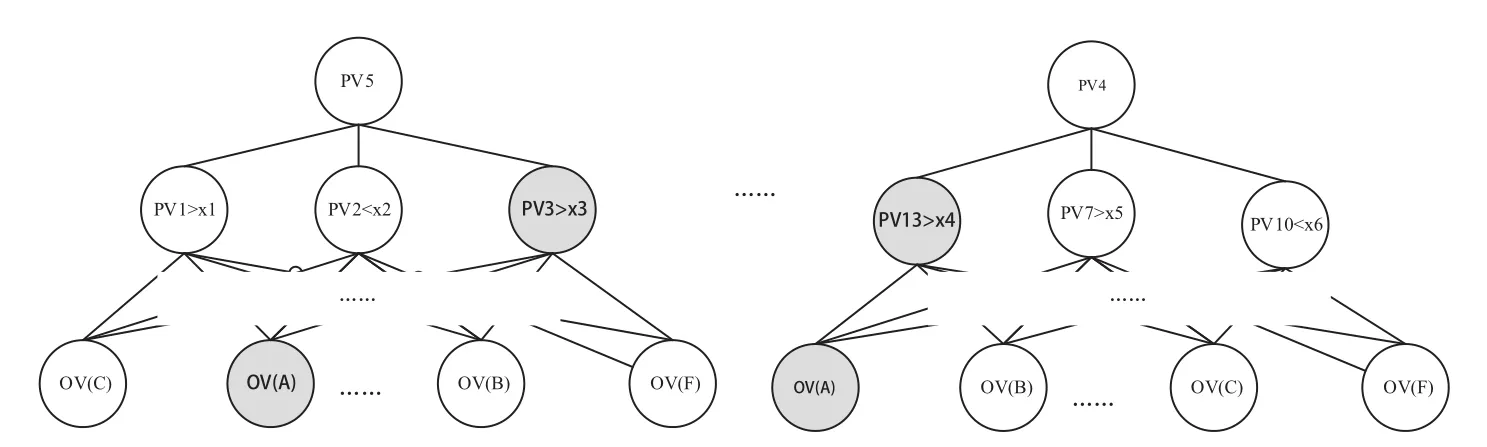
图2 随机森林模型预测流程示意图
从图2可知,当两位学生的在线行为数据较为相似而学习成绩分类不同时,某一数据的细微差距可导致决策树中对两位学生的预测结果不同。随机森林模型通过划分学生和建立多棵决策树识别这种差异。表2的结果为教师提供的信息是,教师可使用该预测模型判断班级所有学生在当前在线学习状态下可能取得的最终成绩,且预测正确的学生数量为全班学生总数的74.7%。
混合课程学生成绩的整体预测准确率不能直接引导教师优化混合教学,本研究将学生成绩分为五类后进一步提升了预测结果的可解释性。如表3所示,在对每个学生个体成绩等级进行评价时,评价方法采用二分类评价,即只判断预测结果是否属于当前成绩等级,因此表3中各等级成绩的预测查准率就是模型对当前成绩等级的预测结果。在本研究中,混合课程中成绩为A和B的学生被预测准确率最高,分别达到80.6%和85.3%。同时,成绩为A和B的学生其预测查全率也有很高数值,分别达到74.8%和85.3%,说明其他成绩的学生被预测为A或B成绩的错误率较低。此项结果表明,当教师使用该模型对全班学生的学习成绩进行预测时,可识别大多数成绩为A和B的学生,从而将精力更多放在成绩较低的学生中。
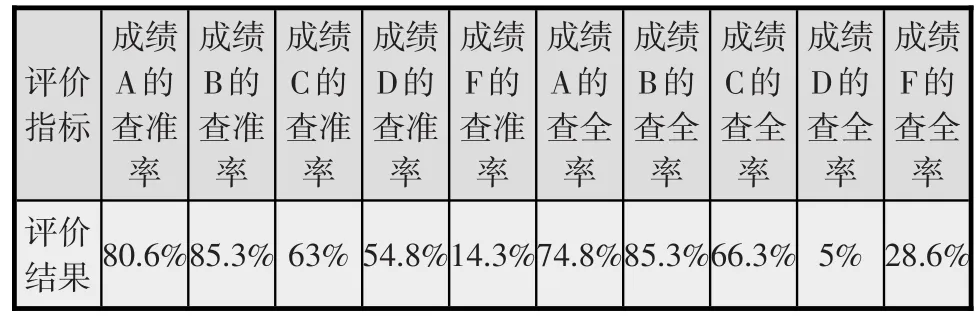
表3 混合课程中各成绩等级学生预测结果评价
为进一步解释本研究中学生在线学习行为各指标对学习成绩预测的影响,记录了学生在线学习行为对学习成绩预测的重要性(如图3所示)。在随机森林模型中,预测变量重要性是指预测变量对结果变量预测准确率的贡献,而非对结果变量的解释(Du,et al.,2021)。通过比对样本的变量和重要预测变量可判断当前样本的预测结果是否可信(Ribeiro,et al.,2016)。如图3所示,学生在线学习行为指标作为预测变量时,各项指标之间在重要性上的差异都小于0.2,且没有任何一项或几项指标对成绩预测结果产生了显著影响。此项结果表明学生所有在线学习行为对学习成绩预测的影响较为平均,当学生个体在所有在线学习活动中均有较多行为数据时,本研究模型所得预测结果具有较高可信度;当学生个体在某项或某几项在线学习行为指标上没有数据时,模型对其预测的结果可信度较低。
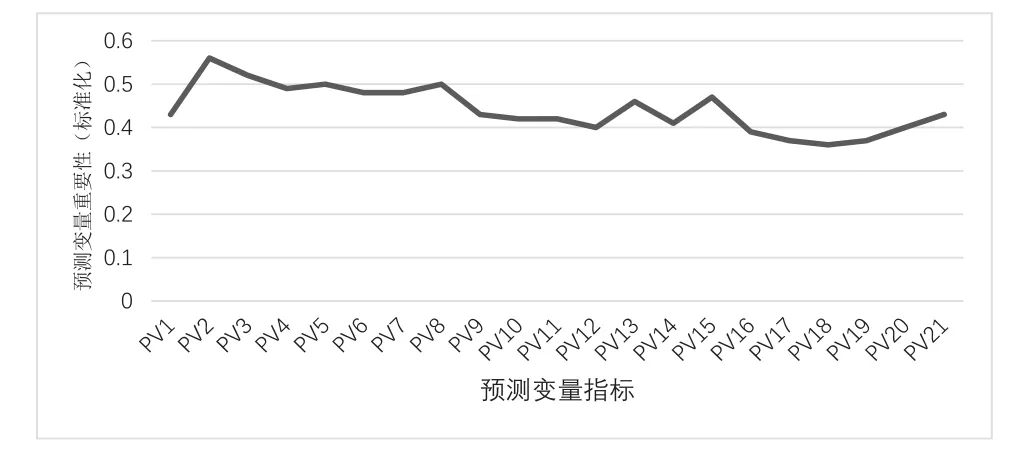
图3 预测变量重要性折线图
五、研究结论
(一)研究结论
应用人工智能变革教育教学实践的关键问题是人工智能的可解释性(孙众,等,2021)。作为人工智能基础的机器学习是在教育教学场景中应用的主要技术(蒋鑫,等,2020;郑勤华,等,2019),探究如何解释基于机器学习的学生成绩预测模型可为人工智能教育应用的可解释性研究和实践提供参考。
本研究综合学习分析和计算机科学两个领域对机器学习技术可解释性的研究发现,在教学场景中解释基于机器学习的学生成绩预测模型主要关注三个方面:预测模型结构所代表的教育意义、预测模型内在推理机制所揭示的预测关系和预测结果对教学实践的启示。基于一所高校一学期的混合课程数据,构建基于学生在线学习行为的学习成绩预测模型,并解释了五种以机器学习算法构建的学习成绩预测模型。结果表明:①只采用学生的部分学习过程数据预测学习成绩时,学生的行为模式与学习成绩的映射关系存在多种模式,试图构建学生在线学习行为与学生成绩一一对应预测关系的预测模型难以获得较好的预测结果。②本研究中的预测模型最高可预测正确所有混合课程中74.7%的学生,不同学习成绩等级学生的预测准确率差异较大,成绩为A和B的学生其被预测准确率较高,达到80.6%和85.3%,成绩为C及以下的学生其被预测准确率最高只达到63%。③本研究对学生个体的预测结果只有当学生积极参加所有在线学习活动时才具有较高可信度,当学生个体出现在线学习活动缺失时预测结果可信度较低。
(二)在混合课程场景下应用成绩预测模型的建议
2016年,在混沌计算机俱乐部第33届会议上,有人提出通过将人脸或车牌印刷到衣服上“伪装”自己从而反制当前零售行业生物数据收集以及政府隐私数据收集的方法(EDRi,2016)。学生在混合课程中的学习过程包括线上和线下两方面,从本研究仅基于学生在线学习行为数据预测学习成绩的结果可发现,当学生的在线学习行为较少,或只做出单一种类的在线学习行为时,更容易“伪装”自己的学习成绩,无论使用何种机器学习算法构建预测模型,预测结果都是不可信的。
在当前使用机器学习算法预测学生成绩的研究中,学者们关注的重点仍是收集什么数据,怎样优化算法以获得更高的预测结果准确率(Baker,2019;吴永和,等,2020)。混合课程场景的多样性和灵活性不可能被几种数据完全描述(牟智佳,等,2018),解释当前研究中准确率较高的预测模型从而促进教学实践的关键在于,发现混合课程中对成绩影响最为显著的学习行为,发现学习行为与成绩的多重对应关系,从而丰富教师实施混合教学时的个性化教学方案。
本研究通过比较多种以机器学习算法构建的基于学生在线学习行为的混合课程学生成绩预测模型,为教师在混合课程场景下应用成绩预测模型提出如下建议:
1.针对混合课程特点应用预测结果
本研究中的样本均来源于学生在线学习行为活跃度较高的混合课程,但从不同预测模型得到的结果来看只有随机森林模型预测结果较好。这说明混合教学中学生可通过多样化的在线学习获得较好成绩,达成教学目标的在线学习行为模式不止一种。教师应建设多样化的在线课程活动,给学生提供更多学习机会,从而满足不同学习偏好学生的学习需求,达成混合课程目标。同时,教师应关注预测成绩较差的学生,具有较高的在线学习活跃度却被预测成绩较差表明学生可能在学习方法或心理等其他方面出现了问题。
2.理解模型的推理机制以灵活切换预测模型
当前在完全在线课程和混合课程情境中,多种以机器学习算法构建的成绩预测模型都被证明有较高准确率。然而,本研究的结果表明相同混合课程中以不同算法构建的预测模型具有不同的预测结果准确率。这说明教师应对机器学习算法的预测推理机制有基本的了解,从而分辨所使用的成绩预测模型是否可持续优化教学。在混合课程的教学设计发生变化时,灵活使用依据不同预测推理机制构建的预测模型有助于获取更准确的教学干预依据。
3.依据学生在线学习行为的完整性判断预测结果是否可信
通过成绩预测模型呈现班级或课程所有学生的预测结果为教师带来的信息有限,教师更希望了解每个学生的独特学习模式以实现个性化教学。因此,使用成绩将学生分为多个类别并实现预测,相较于将学生分为合格/不合格更具有教学意义。另外,在预测模型中,预测变量的重要性并非对结果变量形成的解释,而是对得到准确预测结果的贡献(Ribeiro,et al.,2016)。本研究发现,若学生个体未参与某种或某几种在线学习活动时,对其的预测结果可信度较低。教师可依据学生在线学习行为数据是否有缺失来判断是否依据学生个体的预测结果为学生提供个性化的帮助和支持。

