公路基坑降水引起邻近地下管线变形性状

文 / 北京市政建设集团有限责任公司 付天宇 包余阳

引言

城市发展中很多大基坑应运而生，开挖过程中对地下管道带来很大的影响，要有效的避免地下管道遭到破坏，必须对其采取合理的加固措施，分析基坑降水对地下管线的变形性状有应用的现实意义。

地下管道变形状态的相关指标

进行地下管道的施工中，管线安装的安全性其主要的决定因素是其沉降的差异及线管的应力，其中柔性管道的接头可以进行转动，会经常会因为接头变形的因素出现变形度情况。而刚性管道不能进行转动，则不容易发生变形的情况。

作者通过利用管线沉降梯度与管线接头的张开度数值的因素来进行科学的判定，通过合理指标对管线的变形状态进行分析。

管线沉降所需求的梯度

利用换代分析法作为参考进行坐标的建立，其管线一侧的端点设置为O 点，沿管线的方向作为 X 轴，管线沉降方向作为 Y 轴，将管线沉降后的每个点都看出单独的坐标（如图1 所示），将O 点当成原来的起点，每隔0． 2S沿X 轴取新的坐标( X，X) ( j = 1，2，3……n)，从而得到相邻两个纵横坐标差的比值，我们将它看作管线沉降的梯度。

管线接头的张开度数值

（见图2 所示），将地基沉降曲率的半径设为R，其管道节的长度为L，将管线接头的张开度数值设为Δ，通过几何关系计算而得出：Δ/D = L/R，将管线的允许张开度数值设为[Δ]，通过公式（2）可以得出允许的曲率为：1 /［R］=［Δ］/( L·D)，并通过基坑降水中管线的沉降曲线求出管线的接头曲率，以此来对管线的破损程度进行预判，如图3 所示。

建立有限元的分析模型

工程概况

某市有一深基坑的长度是156m，宽度是65m，深度为14m，深坑外围的静止水位是7m，预埋管线位于基坑的西侧，预埋方向与基坑保持平行，中心处的埋深为3m，中心线与坑边缘的距离为6m。

计算的相关参数

通过岩石的工程勘验报告显示，计算出土层的分布与模拟参数的取值如表1 所示。此次计算的土体材料的屈服性借助了Drucker － Prage 的屈服标准，并充分结合当地的施工经验，将自重应力下5 别的压缩模量当成土层的弹性基础来进行计算。还考虑了接触面管道与土壤的相互性作用，将其摩擦系数取值为0．25。

模拟结果的分析

管道基坑的开挖过程中会面临众多影响地下管道导致其变形的形状，其中包含了降水的静止深度、埋管位置的土壤性质、地表的沉降问题、管线的直径大小、开挖法计算方法与土壤的弹性模量等因素，因为基坑的降水深度给管道的变形影响效果比较大，因此选择此因素进行对应的数值模拟。

进行数值模拟的过程中，取其降水深度为8～28m范围内，间隔4m 选取其中一个深度值，选择6 个深度值来对降水深度的基坑给地下管道带来的影响进行分析。

管线沉降

当降水深度在8m 位置时，测试柔性管道的管线沉降曲线图形如图4 所示，由图4 可以看出，当降水深度在8m 位置的时候，降水漏斗的中轴线与柔性管线的位置进行了重合，其管线的沉降量处于最大的位置，当漏斗的中轴线与管线的间距逐渐拉开，其管线的沉降量会持续的下降，随即其下降的速度呈现先增后减的形态。当管线的沉降变成“s”型时，当中拐点处于降水漏斗中轴线与管线的间距在98m的位置上。

当基坑的降水深度处于8～28m 米范围内，基坑临近的地下管线沉降范围如图5 所示，当底下管线的总沉降量不能均衡时，沉降量会由于降水深度的增大而提高。

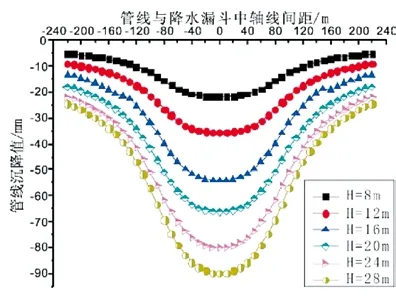
管线的沉降梯度

当降水量为8m 的位置时，其管线的梯度处于最小值，当管线逐渐与降水漏斗的间距拉开时，管线的沉降梯度也得到了不断地增大，在简约处于70m 左右的位置其梯度处于最大值，随后间距的增加中其梯度又逐渐的变小。

结语

加固区是基坑相邻管线的受力变形最大的位置，其中与柔性管线相邻的重点加固区域在降水区域边界线范围内，其降水面积的深度越小，其加固区域与降水区域的边界线越近；而刚性管线的重点加固范围则是降水漏斗的中轴线附近。当降水区域的边界线处于40m 时，柔性管线的接头曲率出现了极值，所以将此区域看成柔性管线的重点加固区域。而刚性管线的降水区域边界线是周边40m 范围内为受压区域，而其它区域则会承受拉力。