流体力学教学中课程思政的融入与探讨

樊艳红，常超，贾有，张俊婷，陈静

（1. 太原科技大学 应用科学学院，山西 太原；2.山西省教育科学研究院，山西 太原）

一 引言

当今时代，高等教育至关重要。以立德树人为任务，高校所有课程，引入“课程思政”。其中有不少成果[1-6]。流体力学是很多工科专业，一门的技术基础课。在其教学中，加强“课程思政”较关键。本文着重进行：课程思政融入流体力学教学的实施与探讨，具体如下：首先，优化流体力学知识体系，将零散的知识点模块化，使学生容易掌握流体力学知识内容，对内容触类旁通，激发学习兴趣。其次，通过穿插历史名人、引入著名工程以及阐述基本理论和方法等等，润物无声地穿插思政元素，让学生崇尚科学，尊重科学，要有科学的家国情怀。使学生在掌握基础知识的同时，提高能力，激发学习兴趣、探索精神。

二 优化流体力学内容知识体系

流体力学课程知识面广、内容多，包含许多理论及公式。本课程由流体的宏观、微观、静动结合等方面出发，理论知识，提高能力，激发兴趣、增强创新意识。笔者讲授流体力学课程，在讲授知识点，引入课程思政之前，先优化流体力学知识体系，具体如下：针对流体力学知识，以三大守恒定律出发，建立内容体系，如图1所示，将零散的知识有序化，将内容进行梳理，形成模块化的课程体系，让学生能够对流体力学内容触类旁通[7]。

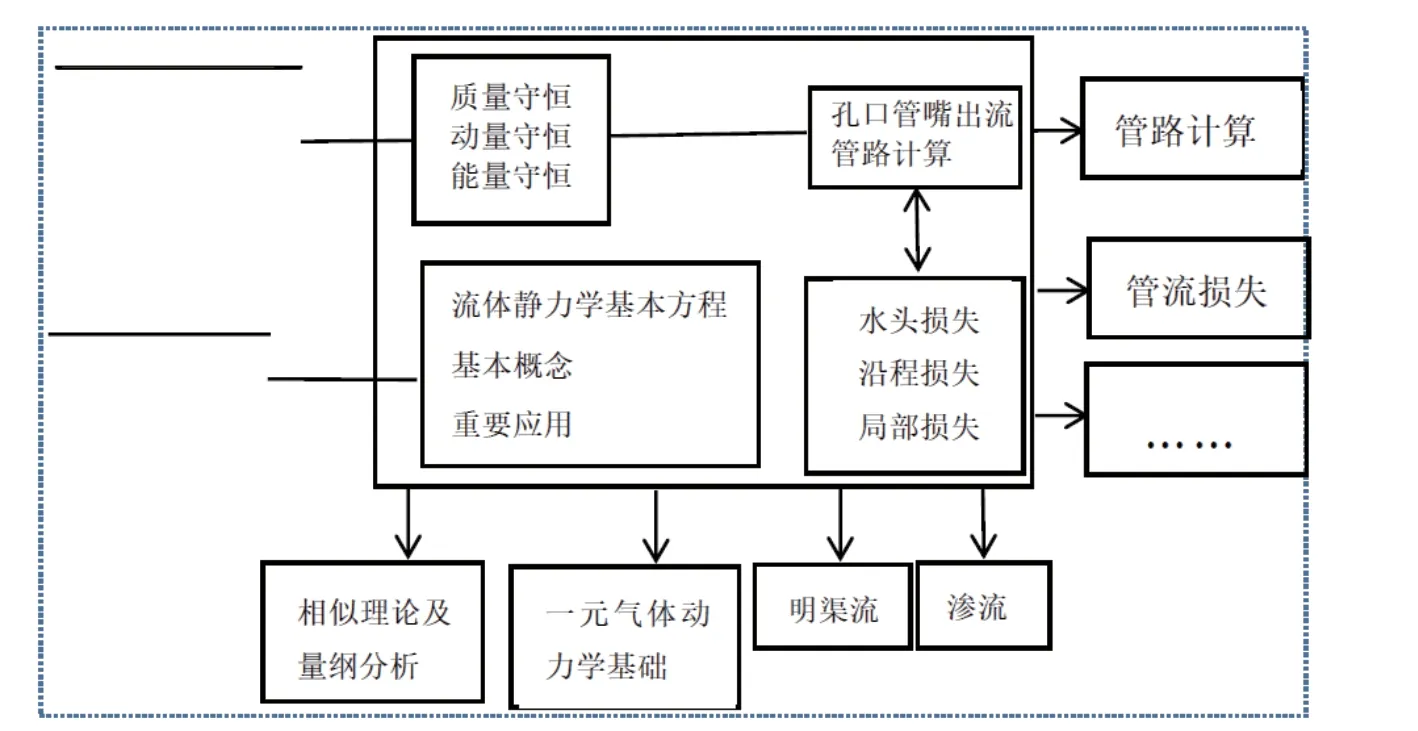
图1 流体力学内容知识体系图

针对流体力学实验，利用杭州奔流科技有限公司[8]研制的虚拟设备进行实验，该公司利用浙江大学原有流体力学实验技术，结合自主研发的流体力学技术，研发出功能更加完善的流体力学水力学实验设备，无缝承接并延续推广全国多所高校流体力学实验室的设备及售后服务。本课程因为课时的限制，主要开设了流体静力学、雷诺、能量方程、动量方程等实验。通过实验：一方面、可以更深入掌握理论及方法；另一方面、可以提高学生解决问题能力，调动其积极性，激发其潜能。

三 流体力学课程思政元素的融入

流体力学课程思政元素的融入，仍需以流体力学知识的主菜烹调工序（授课顺序）为主线[9]，但是在主菜处于不同火候的时候，根据主菜的特点，添加思政元素的调料，料的量既不能多，也不能少，只有做到适时和适度，才能烹调出流体力学专业知识的“美味”。相同的菜品和调料，在不同级别厨师的手中，很可能会做出不同的味道。如果教师是“厨师”，备课和上课就是烹调技能和思想美食的过程，学生则是美食的享用者。流体力学教学，也如此。只要用心挖掘、提炼，坚持知识传授、能力培养结合，“思政之盐”，必将融入“育人之汤”。流体力学教学中，课程思政，一直在路上，任重道远。本文在流体力学课堂上，从思政角度，对流体力学内容从深度的精准把握，要求教师不仅要有思政意识，具备精心备课的工匠精神，而且对流体力学内容要有深度挖掘的能力。流体力学课程思政元素的融入具体做法如下：

（一） 通过历史名人讲授课程思政元素

伟大的科学家牛顿（Newton）探讨了：粘滞力的计算。帕斯卡（Pascal）、阿基米德（Archimedes）分别给出了液体压强的求法、浮力的计算公式。约瑟夫·路易斯·拉格朗日（Joseph-Louis Lagrange）给出了理想液体的平衡微分方程式，他还运用动能定理推导出了著名的能量方程（伯努利方程）。这些科学家通过辛勤工作，不怕艰难险阻，取得显著成果。我们应该铭记他们，尊重其科学成果，在实践中发扬光大该科学精神[10]。应该好好研究其理论内容，而且要在此基础上有所启发，有所突破，有所创新。

我国科学家湍流理论奠基人周培源[11]在湍流研究方面做了巨大贡献。他给出了“湍流模式理论”，其理论扎实，功底深厚。其不怕吃苦，认真钻研的精神值得我们深入学习，并好好研究其理论内容，而且要在此基础上有所启发，有所创新。另外，为了纪念周老，有了每两年一次的“周培源”力学竞赛。我国著名科学家钱学森，在火箭和导弹发射贡献巨大。由此，让学生有民族自豪感，自信起来，树立爱国热情，启发学生对科学的家国情怀。

（二） 通过典型工程引入思政元素

在课堂上，当学生了解到四川的都江堰[12]神奇的结构设计，看到在汶川大地震中二王庙已坍塌、受损严重，但经历两千余年的都江堰却安然无恙、依然正常运转时，无不惊叹于都江堰所创造的千古奇迹，惊叹于中国古代人民改造自然的神奇力量，民族自豪感油然而生。

陕西郑国渠、广西的灵渠，赵州桥[13]都是人类智慧结晶，其工程闻名中外，可见，其可以提升民族自豪感，树立自信，激发爱国热情。这些工程，体现了中国民族的智慧，展现了他们的勇敢、勤劳，在科技迅速发展的当今，我们仍要继承、发扬中华民族勤劳、勇敢等优良传统，并发扬光大，更加勤奋、刻苦学习，努力工作，这样才有利于我们个人的发展、集体的发展、乃至整个国家的发展，不断进步。这样讲解，让学生有民族自豪感，自信起来，树立爱国热情。另外，掌握专业课同时，要有意识保护好历史瑰宝[14]。

（三） 通过基本理论和计算方法的讲解引入思政元素

首先、针对提高逻辑思维能力，精心设计，推导连续性方程。推导中，引入思政元素。具体如下：

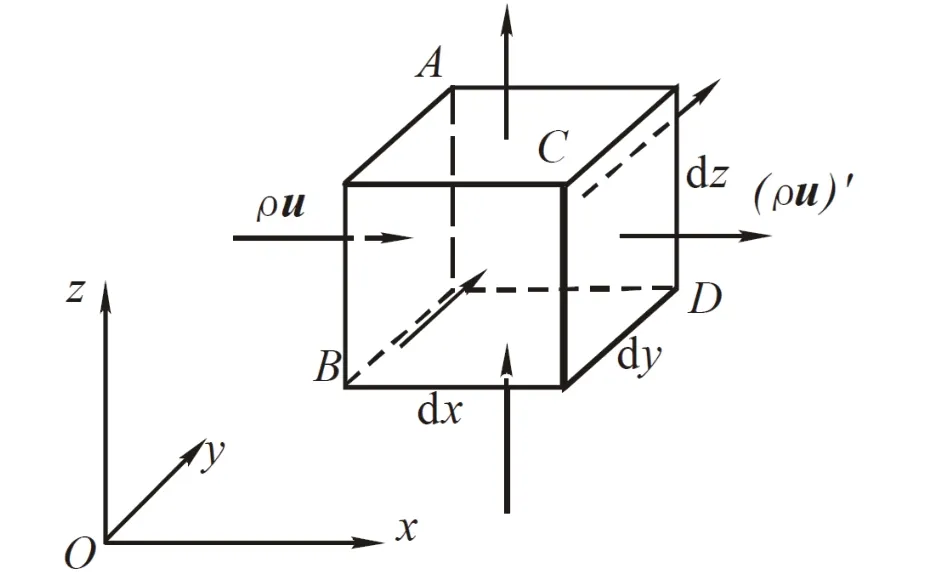
图2 六面体单元示意图

进一步简化，二维时，方程为

上式理想流体、实际流体都适用。进一步简化，对于管道中流动的流体，其属于一维流动的问题。取一微元流束，如图3所示，设定常、连续流动，则

图3 微元流束示意图

讲解流体阻力和能量损失[15]时，沿程阻力系数的计算：

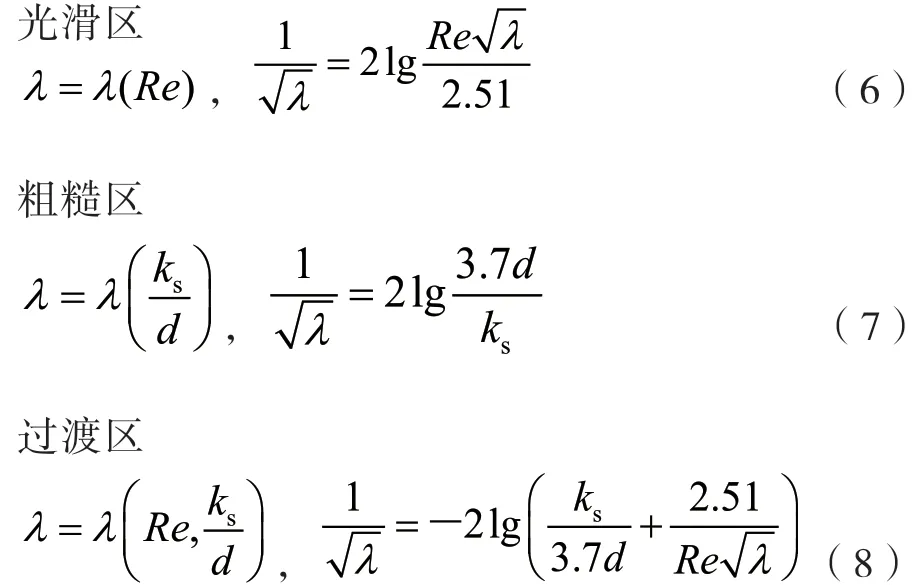
以上函数均为隐函数，无解析解。通常采用迭代法求解。迭代时，初值选取不同，迭代过程不同，不会影响最终结果。因此，可引导学生，不要看重入学的成绩，不要太介意之前课程的成绩，只要选定本课程学习目标，好好学习，不怕刻苦，努力拼搏，坚持不懈，认认真真，不断总结做错题的经验和教训，一定能实现目标。

推荐理由:在《老照片》陆续出版20年之余，编辑了这套温情系列图书。其中有些文章从已刊《老照片》中精心挑选适合青少年读者阅读的温暖篇章，文字质朴平实，感情自然真挚。还有一些文章，按照《老照片》的一贯格调，另约稿、辑录了众多名家的作品。冀望与更多的青少年读者一起成长，通过共同翻看《老照片》，开阔阅读视野，增长人生阅历，增添人文情怀。

粘流中，边界层理论非常重要。湍流理论属于世界难题之一，其著名的研究成果有卡门涡街现象。对其研究，在此基础上，有所创新。解决问题时，要采用辩证思维，思维要有逻辑性，不能绝对，要静观其变，在变化中找普遍规律，从整体发现其局部变化的规律。

描述明渠流或其他流道，采用圣维南方程组，其由质量守恒定律、动量守恒定律推导得到。时间不同位置不同水力要素不同。采用该方程组求解结果准确。可见，解决问题时，要从整体把握解决问题的关键方面，抓住主要方面，整体分层递进把该问题解决，其实，解决任何问题，抓住主要方面是解决问题的关键。

工程中很多问题的求解，常常无解析解，通常需要求解偏微分方程组，故，用数值模拟方法分析。工程中广泛用到求解三维可压缩Navier-Stokes（简称N-S方程）方程如下：

其中，Q、F、Fv分别为流动守恒变量、无粘（对流）通量、粘性通量，各项具体如下：

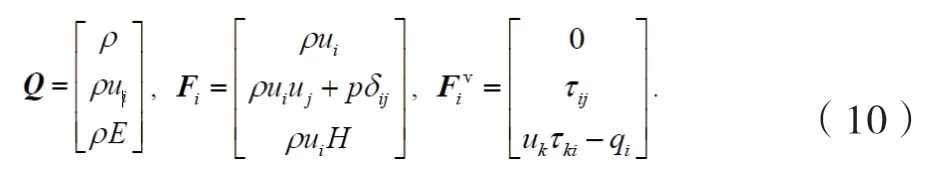
这里，流入流体的密度（ρ）、流体的速度分量（ui）、系统的总能（E）、流体的表面压强（p）、系统的总焓（H）。总能与总焓满足：

对于完全气体，温度和压强满足：

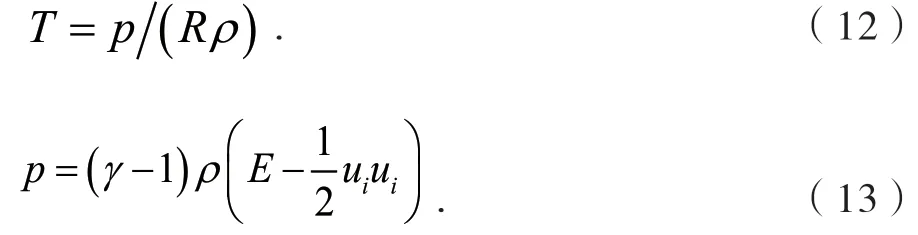
式中，γ为比热比，空气取1.4，R为气体常数。此外，对于牛顿流体，粘性应力和热传导分别为：

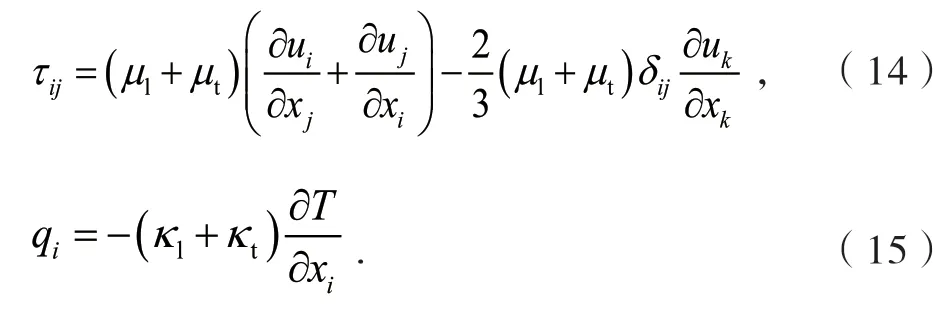
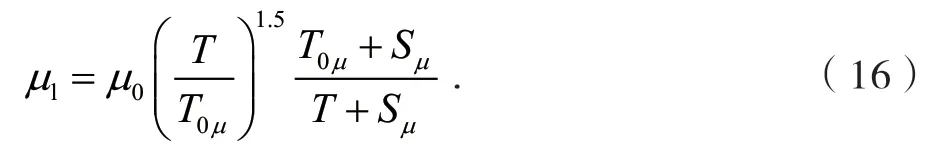
μ0是参考温度T0μ下的粘性系数，Sμ为Sutherland常数。κl、κt满足：

这里，Prt、Prl分别为湍流、层流普朗特数。对上述方程进行时间、空间离散。采用二阶迎风格式得到合理的数值模拟结果，如图4、图5分别为机翼1、2的压力云图、等值线图。可见：所有事情都应按照客观规律办理；要个人利益服从集体利益，要有团队意识，注重集体的力量，才能取得更好发展、更大进步。

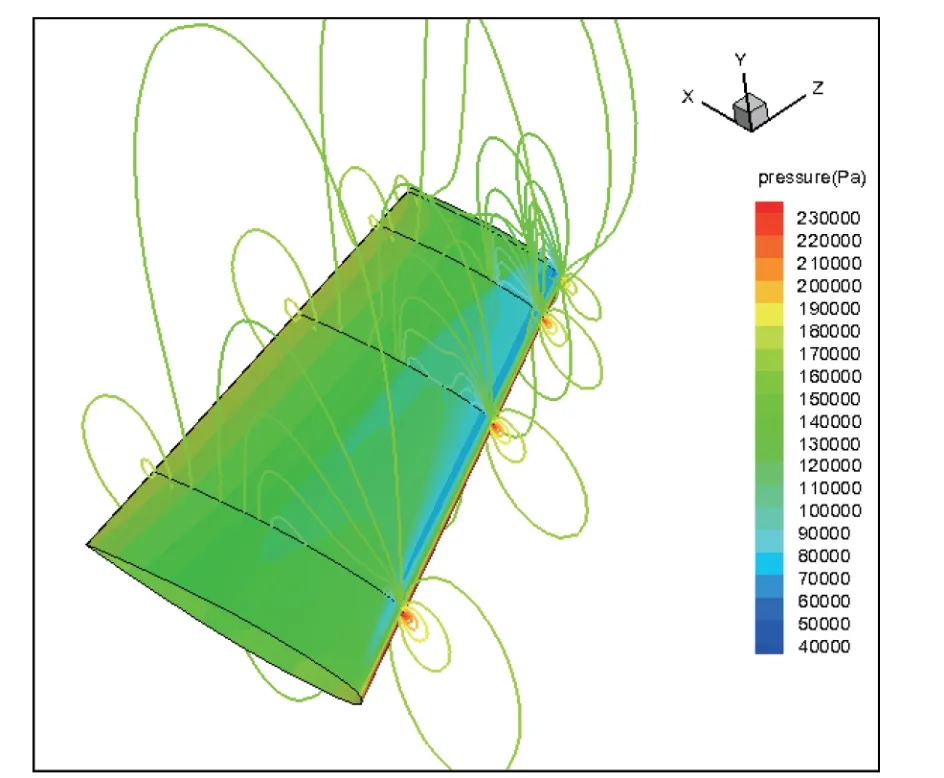
图4 机翼1表面的压力云图及典型等值线图

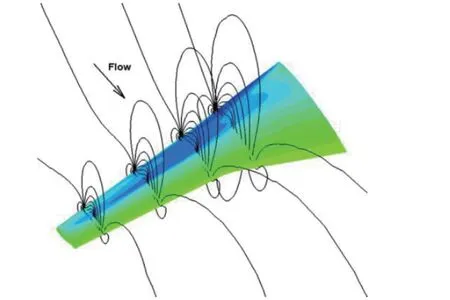
图5 机翼2表面的压力云图及典型剖面等值线图

讲授“气体动力学”时，首先，介绍高超声速飞行器的知识[16]，其次，为学生展示荷兰代尔夫特大学所设计的低粗糙度敏感性的某翼型，状态（马赫数Ma=0.2，雷诺数Re=9.0×106，两种攻角：a)α=6°、b)α=15°）的压力系数等值线、流线，如图6所示，学生可以对典型外形的流场有清晰的认识，通过讲解，可以激发其好奇心，培养其科学兴趣及探索精神。

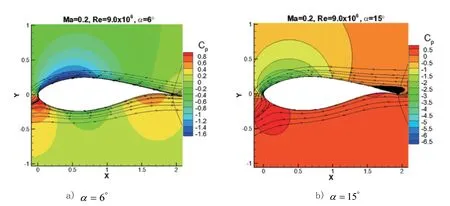
图6 某翼型的压力系数等值线和流线(α=6°、α=15°）

四 结语

本文结合流体力学内容，首先，对教学内容，进行梳理，模块化整理，优化内容，其次，通过穿插历史名人、引入著名工程以及阐述基本理论和方法等等，润物无声地，引入思政元素，尊重科学成果，要有科学的家国情怀。使学生以民族为自豪感，自信起来，树立爱国热情，启发他们对科学的家国情怀，在掌握基础知识的同时，提高能力，激发学习兴趣、培养探索精神。