基于GA改进BP神经网络预测热变形流变应力模型的建立
汪雅婷,黎俊良,袁楷峰,陈广义*
(1 佛山科学技术学院 机电工程与自动化学院,广东 佛山 528200;2 西安热工研究院有限公司,西安 710054)

与传统的BP神经网络模型相比,遗传算法(genetic algorithm,GA)的添加能在有限的训练数据中进行数据优化,通过优化输入层、隐含层和输出层的初始权值、阈值,减少了收敛到局部最优的可能性[15],增强实验数据与预测数据的相关性,避免如BP神经网络模型在训练学习新样本数据时遗忘旧样本及输出结果可能趋于局部最优解的缺点。而与蒙特卡罗的随机模拟相比,GA通过重组和变异的方式,使得数据信息“繁衍进化”,优化预测结果。本实验通过分析应力-应变曲线,采用GA对BP神经网络预测应力-应变模型进行改进优化,对比了BP神经网络模型和改进优化后的BP神经网络模型的准确性。GA改进型BP神经网络模型的建立有助于预测金属不同变形温度下的应力-应变曲线,为实际热加工提供优化工艺、提高产品质量的理论指导。
1 实验材料与方法
实验材料为结构用钢普遍采用的Nb-Ti-V微合金钢,其主要化学成分(质量分数/%)为:0.12 C,1.47 Mn,0.01 Ti,0.007 V,0.042 Nb,0.25 Si,0.018 P,0.009 S,0.0039 N,Fe余量。利用线切割机对铸造样坯切割出圆柱状试样(φ10 mm×15 mm),使用Gleeble-3500热模拟机对试样进行等温恒应变速率压缩实验,压缩变形量均为60%,变形温度分别为1000,1050,1100,1150,1200 ℃;应变速率分别为0.01,0.1,0.5,1,3 s-1。将试样放置热模拟机中,以10 ℃/s的升温速率加热至变形温度后保温30 s,然后以不同的应变速率进行压缩实验,变形结束后立即水冷至室温。实验过程中,热模拟机内需保持真空环境,试样两端添加金属垫片,以减少由于端面摩擦而对测试数据产生的影响。实验数据通过热模拟机中自带的数据采集系统软件采集,从而得到不同应变量下的流动应力值。
2 应力-应变曲线分析
金属的热变形过程中必然存在着加工硬化、动态回复甚至动态再结晶。图1为不同应变速率下Nb-Ti-V微合金钢的应力-应变曲线,从图中可以明显看出,随着应变量的增加,变形过程中应力急剧升高然后减缓,最后应力随着材料的变形量增加而下降。这是由于在变形的初始阶段(ε<0.1),加工硬化随着应变量增加而增强,从而导致应力的上升;随着应力达到峰值应力后,动态回复与动态再结晶的相“较量”会导致不同应力-应变曲线出现。当动态软化弱于加工硬化时,应力会随着应变的增加而持续上升并无峰值应力的出现;当动态再结晶和动态回复的软化效果强于加工硬化时,应力会随着应变的增加而下降并出现峰值应力,应变的持续增加,材料中的软化效果会与加工硬化达到平衡,应力-应变曲线趋于平稳,进入稳态流变阶段。图1(e)中Nb-Ti-V微合金钢的部分应力-应变曲线的应力值随着应变在0.7之后的增加而呈现上升趋势。这是由于在具有较高层错能的Nb-Ti钢中,动态再结晶的回复效果发生一定程度上的减弱,从而导致加工硬化再次占据主导地位,应力-应变曲线出现“上翘”[16]。Nb-Ti-V微合金钢在同一变形温度不同应变速率下的应力-应变曲线如图2所示。由图中可以看出,同一应变、同一温度下流变应力随着应变速率的增加而增大,应力-应变曲线中峰值应力随着应变速率的增加而增大,其对应的应变值也增大;而在同一应变和应变速率下,流变应力随着变形温度的升高而降低,峰值应力随着变形温度的升高而降低,峰值应力对应的应变值减小。应变速率的提高意味着完成相同变形量的时间减少,位错的湮灭速率小于增殖速率,位错累积导致流变应力提高;变形温度越高,原子的扩散和运动越剧烈,代表着Nb-Ti-V微合金钢中的位错更轻易摆脱第二相粒子的钉扎作用,致使流变应力随着变形温度的升高而明显降低。

图1 不同应变速率下不同温度的应力-应变曲线
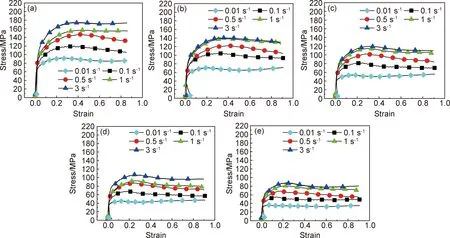
图2 不同变形温度下不同变形速率的应力-应变曲线
3 GA改进型BP神经网络模型的建立
3.1 样本的选取

(1)
(2)
式中:Z为Zener-Hollomon参数;Qdef为热变形激活能,J·mol-1;R为气体常数,J·mol-1·K-1;T为绝对温度,K;α,A,n均为材料常数。
在现有的人工神经网络模型中,BP神经网络是一种预测金属高温变形行为的有效方法。而温度、应变速率和应变作为金属热变形过程中影响流变应力大小的重要参数,在神经网络模型中需作为输入层参数,输出层为流变应力。GA算法在全局范围内搜索得到训练所需的最优权值和阈值,再输回BP神经网络模型中进行局部搜索从而得到误差更小的预测值。本实验工作所建立的GA改进型BP神经网络模型的运行结构示意图如图3所示,其中隐藏层结点个数为i,输入层到隐藏层的权重为U,隐藏层到输出层的权重为W。

图3 GA改进型BP神经网络模型结构
Nb-Ti-V微合金钢的25组热模拟数据中,为了保证训练数据量,选取23组数据作为模型训练数据,2组作为测试数据。其中,训练数据包含了应变速率0.01~3 s-1、变形温度1000~1200 ℃,而测试数据为应变速率0.5 s-1、变形温度1050 ℃和应变速率1 s-1、变形温度1100 ℃的热模拟数据,具体数据划分如表1所示。
3.2 归一化处理
(3)
式中:X′为归一化得到的数据;ymin,ymax为归一化处理中的两边界值,即为0和1;x为样本数据;xmin,xmax分别为样本数据中的最小值与最大值。而在模型输出结果后,需要将其进行反归一化后,结果转换为应力值再进行误差分析,数据反归一化遵循:
y′=(y-ymin)(xmax-xmin)+xmin
(4)
式中:y′为反归一化后得到的数据。
3.3 训练参数设置
在评估模型数据的多样性时,均方误差(RMSE)越低,可显示模型预测效果越好。而确定隐藏层的神经元数量是至关重要的,设置“合适”的神经元数量能提高模型的计算精度。本模型在确定隐含层神经元个数n1时,遵循的经验公式为[20]:
(5)
式中:m为输入层节点数目;n为输出层节点数目;a在[1,10]范围内取任意自然数。控制模型训练次数为2000,学习速率为0.01,目标训练误差为0.0001的条件下,根据经验公式进行穷举运算,得出隐含层神经元个数取[3,12]之间自然数时的均方根误差,确定最佳隐含层节点数,其中均方根误差(RMSE)公式为:
(6)
式中:Ei为实验值样本;Pi为预测值样本;N为样本的总数。模型运行所得均方差结果如图4所示,可以看出,随着神经元个数的增加,训练集均方根误差显著减小,当隐含层神经元个数为12时,RMSE值达到最小。因此,可确定最佳BP神经网络模型的网络结构为3-12-1。
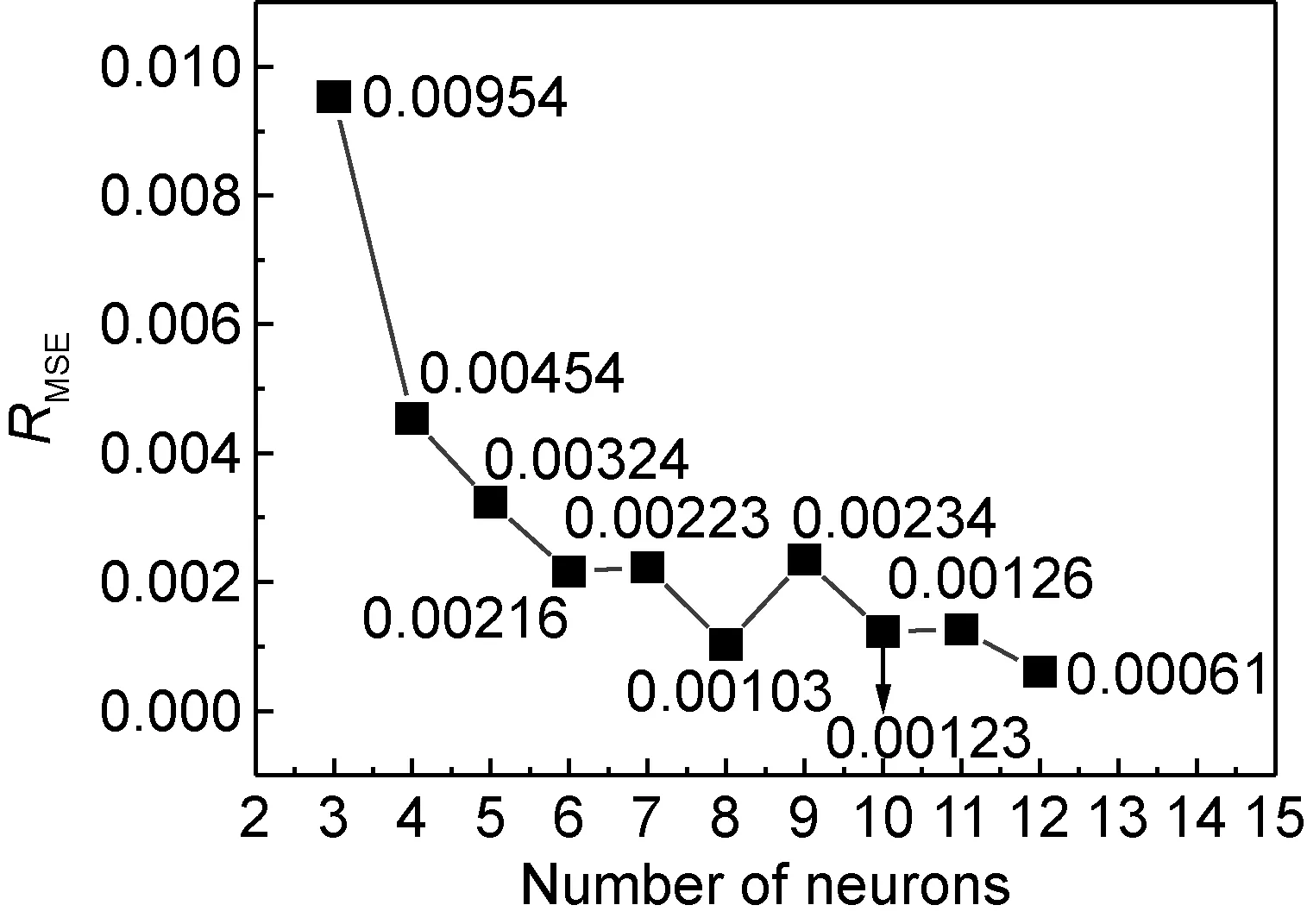
图4 确定过程中隐含层节点数与训练集均方根误差的关系曲线
构建出最佳BP神经网络模型后进行训练,设置训练次数为2000,学习速率为0.01,动量因子为0.01,训练误差设置为0.0001。
3.4 误差反向传播过程
各输出层神经元的输出误差被计算记录后,模型会通过误差梯度下降法对各层的权值和各层的节点阈值进行调整,会得到较为优异的输出值,且接近期望值。
每个输入层的二次型误差准则函数为[15]:
(7)
式中:p为训练数据样本;Ep为神经网络在第p个样本输入下的偏差;L为输入结点总数;Tk为第k个节点的实验值;Ok为第k个节点的输出值。
模型对p个训练数据的总误差准则函数为:
(8)

则输出层权值的调整公式为:
(9)
式中:wni为连接输出层的第n个神经元和稳藏层的第i个神经元的权值;Δwni为wni的变化量;η为学习速率;φ′为输出层的激励函数导数;netk为第k层网络;yi为输出层第i个神经元的值。
输出层阈值调整公式为:
(10)
式中:ak为输出层阈值;Δak为ak的变化值。
隐含层权值调整公式为:
φ′(netk)·wni·ϑ′(netk)·xj
(11)
式中:wij为连接隐藏层的第i个神经元和上一个隐藏层的第j个神经元的权值;Δwij为wij的变化量;ϑ′为隐含层的激励函数导数;xj为隐藏层第j个神经元的值。
隐含层阈值调整公式为:
φ′(netk)wni·ϑ′(netk)
(12)
式中:θ为隐藏层的阈值;Δθ为隐藏层阈值的变化值。
遗传算法寻最优值阈值参数设置为:训练次数2000,学习速率为0.01,动量因子为0.01,训练目标误差0.0001,种族群规模为30,进化迭代次数为50,交叉概率与变异概率分别为0.8和0.2。
4 模型对比及实验验证结果
测试数据根据式(3)输入神经网络热变形预测模型后,应变速率为0.5 s-1、变形温度1050 ℃和应变速率为1 s-1、变形温度1100 ℃两组测试数据经不同模型输出的预测数据误差结果如图5所示。由图可明显看出,经GA算法改进型BP神经网络模型预测的数据误差基本以0参考线上下波动,并且波动幅度明显小于经BP神经网络模型预测的误差曲线。

图5 不同样本中BP神经网络模型和GA改进型BP神经网络模型输出值的训练误差曲线
测试数据经BP神经网络和GA改进型BP神经网络预测后输出预测结果,并与实验结果相比较,如图6所示。由图6可以明显看出,经实验验证,GA优化改进后BP神经网络模型预测的应力值与实验值有较好的重合度,应力应变曲线动态趋势一致,其重合度要明显优于BP神经网络模型的预测结果。证明采用GA优化改进后的BP神经网络所预测的应力应变曲线具有更优异的精度,能为工业生产轧制工艺提供更好的理论指导,能够大大降低重复做实验的时间成本和材料成本。

图6 BP神经网络(a)及GA改进型BP神经网络(b)预测应力值与实验数据曲线对比曲线
相关系数(R)常用于表示预测数据和实验数据之间的线性关系。R的计算如下式所示:
(13)
式中:N为采集的分析数据点个数;σe为试样热压缩实验所得到的应力值;σp为BP神经网络模型或GA改进型BP神经网络模型所预测的应力值。通过式(13)对GA改进型BP神经网络模型预测结果与BP神经网络模型预测结果进行相关系数计算,得到结果如图7所示,预测数据与实验数据的相对误差分布如图中矩形分布图。模型经GA优化改进后,应变速率为0.5 s-1、变形温度1050 ℃和应变速率为1 s-1、变形温度1100 ℃的预测应力值与实验应力值的相关系数分别为0.99202和0.99734,较BP神经网络模型预测结果的相关系数要更优异。在相对误差分布上,传统BP神经网络所预测的两组热模拟数据的应力值相对误差范围较广,分别在[-2,6]和[-2,4]之间;经GA优化改进后预测的两组数据预测应力值的相对误差主要处在[-2,2]范围内,占70%以上,且相对误差平均值均小于BP神经网络模型的相对误差平均值。

图7 不同条件时,BP神经网络(1)和GA改进BP神经网络(2)预测的应力值与实验值线性关系图、相对误差比值与相对误差值分布图
由于预测值与其实验值相比,部分数据会出现偏高或者偏低的现象,因此需要引入平均相对误差(δMRE)作为模型的评估条件之一,其可以被认为是用于确认模型可信度的无偏统计量,评估预测的准确性和可靠性[21-22]。平均相对误差值(δMRE)[11,23]的计算公式为:
(14)
与预测值和实验值的拟合相关系数相比,平均相对误差更能体现基于GA改进BP神经网络预测模型预测的应力值与实际实验得到的应力值之间的偏差,也能定量评价模型的预测准确性。由式(14)计算得到由BP神经网络模型预测两组测试数据的平均相对误差分别为3.5346%和11.4829%,而由GA改进型BP神经网络预测模型所预测的平均相对误差仅为2.7816%和2.1703%,结合上述拟合相关系数和相对误差的分布可说明所建立的GA改进型BP神经网络预测模型具有良好的预测能力。
5 结论
(1)从BP神经网络模型和GA改进型BP神经网络模型预测的数据与实验数据对比来看,BP神经网络模型经GA优化改进后,预测应力值与实验应力值的相对误差在[-2,2]区间内的数据占比达70%,相关系数分别达到0.99202和0.99734,平均相对误差仅为2.7816%和2.17034%,说明遗传算法(GA)对BP神经网络模型有着良好的优化改进,大大提高了模型的预测精度。
(2)通过测试数据与实验数据的对比分析得出,在较大应变范围内,模型预测结果与实验结果只有较小的误差,经GA优化改进后的模型具有良好的稳定性和预测性,能较好地预测不同热变形参数下的应力应变曲线。

