地震作用下某上游式尾矿坝动力响应分析
龚兴勇,王铭明,杨双钢,胡圣明,苟 超
(1.昆明理工大学 电力工程学院,昆明 650500;2.湖南省水利水电勘测设计规划研究总院有限公司,长沙 410007)
尾矿库是矿山企业储存尾矿渣及澄清尾矿水的重要生产设施[1],我国90%以上的尾矿坝均采用方式简单、管理方便的上游式堆筑。由于特殊的筑坝方式和筑坝材料,使得尾矿坝在地震荷载作用下非常敏感[2],在地震作用下容易坝体失稳,对下游居民的生命和财产造成威胁。因此研究尾矿坝在地震作用下的动力特性尤为重要。
地震的随机性与突发性和坝体空间结构的非均匀性及变异性,致使尾矿坝抗震问题十分复杂,国内外学者主要就地震液化、动位移、加速度等方面进行了研究。AMBRASEYS[3]采用剪切楔理论进行尾矿坝动力分析,分析中只考虑了土体材料的剪切畸变,计算结果不够准确,只能看作近似。汪闻韶[4]分析了不同机理下的砂土液化,分析得出土体处于极限平衡状态下将先于土体液化的发生。因此,本研究以某上游式尾矿坝为研究对象,借助ABAQUS有限元软件运用等效线性原理进行尾矿坝动力分析,通过Fortran语言编写孔压应力模型,对尾矿坝在地震作用下坝体的加速度、动位移、动应力及孔隙水压力进行计算,通过计算结果采用有效应力判别法对尾矿坝的液化区进行判定。
1 静动力分析基本理论
1.1 邓肯—张E-B
静力分析选用国内外许多工程实例证明有效的邓肯—张模型[5]。其切线模量Et为:
(1)
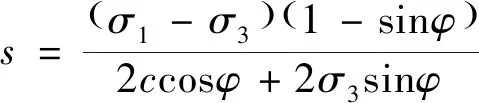
考虑土体材料强度的非线性,内摩擦角可视为随围压变化的函数:
(2)
切向体积模量:
(3)
邓肯—张E-B模型公式中共有9个模型参数:Kb、K、n、m均为实验常数;c为黏聚力;Δφ为对φ进行修正的系数;Rf为破坏比;Pa为大气压。
1.2 等效线性模型
等效线性模型在周期荷载下的滞回性是通过黏弹性Kelvin模型来反映的[6],其应力应变关系为:
τ=Gγ+ηGγ
(4)
式中:τ为剪应力;G为剪切模量;ηG为剪切黏滞系数;γ为剪应变。
剪切黏滞系数ηG为:
(5)
式中:λ为阻尼比,ω为圆频率。
动力反应分析采用沈珠江提出的如下形式:
(6)
(7)
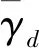
(8)
式中:γdmax为地震过程中的最大剪应变;Pa为大气压。
1.3 孔压应力模型
孔压应力模型采用徐志英和沈珠江建议的公式[7]:
(9)
将式(9)对t求导,并写成增量形式得:
(10)
式中:α为土体的试验参数,取3.0;σ′0为有效应力;τ0水平剪应力;Δug为Δt时间内孔隙水压力增量;ΔN为Δt时间内的振动周数;N为累计振动周数;m为决定孔隙水压力随着α而递减的常数,对于尾矿砂已求得m=1.1~1.2,本文取1.1;θ为试验常数,取0.7;Nt为α=0时的液化周数,其表达式为:
(11)
τav=0.65τmax
(12)
式中:τav为平均剪应力;a、b为尾矿料抗液化性能有关的常数。计算时段等效周数ΔN和累计等效周数Neq采用MARTIN等[8]研究方法,震级和振动持续时间根据表1计算得出。

表1 震级、等效振动次数和振动持续时间的关系Table 1 The relationship between magnitude,time duration,and equivalent cyclic number
1.4 液化判别法
尾矿坝的液化判别方法主要有剪应力对比法、循环应力法、有效应力法等。本研究选用许多工程实例证明有效的有效应力法来作为液化判别的标准。计算公式如下:
(13)
对于三维问题,震前平均主应力的计算采用下式:
(14)
式中:σx、σy、σz为震前应力分量;uw为孔隙水压力。计算得出ks>1,判定该单元完全发生液化;反之,该单元不液化。
1.5 计算步骤
1)采用邓肯—张E-B模型静力计算,根据静力结果算出各单元的最大剪切模量Gmax,取初始阻尼比λ0=0.05。
2)由初始剪切模量Gmax和初始阻尼比λ0形成各单元的刚度矩阵[K]、质量矩阵[M]、阻尼矩阵[C],建立动力平衡方程。
3)计算整个坝体的圆频率ω。
将输入地震时程划分为若干个时段Δt。
5)将计算出的G/Gmax和λ/λmax重新代入进行数值分析,一般迭代3~4次即可收敛。
6)计算该时段Δt内的液化周数Nl,根据表1计算等效周数ΔN和累计等效周数Neq。
7)按式(10)计算该时段的孔隙水压力增量。
8)如此一个时段接着一个时段计算,直至地震结束。
2 工程概况及有限元模型建立
2.1 工程概况
尾矿坝采用上游式筑坝方式,初期坝透水性良好,初期坝顶宽4 m,坝长84 m,上下游坡度均为1∶2,坝高20 m。堆积子坝外边坡坡比1∶4.8,干滩坡比1∶100,考虑正常工况条件,干滩长度取300 m,堆积子坝高为85 m,整个尾矿坝最终坝高为105 m,堆积坝材料分区依次为尾中砂、尾细砂、尾粉砂,具体的材料分区如图1所示,三种材料的渗透系数分别为1.25×10-5、1.85×10-6、1.25×10-6m/s。
2.2 有限元模型建立
2.2.1 边界条件
在计算中根据建设的实体模型,固定坝体底部三个方向的位移,约束其他各面法向位移。在渗流分析时,设初期坝为透水边界,按正常水位考虑干滩长度300 m,在上游边界指定随高程线性变化水头边界。
2.2.2 网格划分
坝体共划分2 720个单元,包括4 103个节点。尾矿坝单元划分情况详见图1。
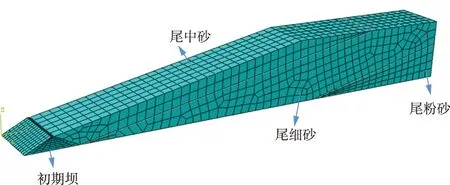
图1 尾矿坝计算模型Fig.1 Calculation model of tailings dam
2.2.3 荷载
计算中所用的荷载主要有自重荷载、水压力和地震荷载,动力时程分析中采用设计院提供的规范谱地震波,该地震波场地烈度为7级,并对其地震加速度进行修改,将地震波加速度峰值调整为0.148 g,经研究认为顺河向地震对坝体造成危害最大[9],因此在下面中值输入顺河向加速度。地震加速度时程曲线如图2所示。地震历时30 s,整个地震过程1 s一个时段,共有30个时段,每个时段采用Wilson-θ法逐步积分,积分步长取为0.01 s,每段地震数据有100个,共有3 000个数据。计算参数见表2和表3。
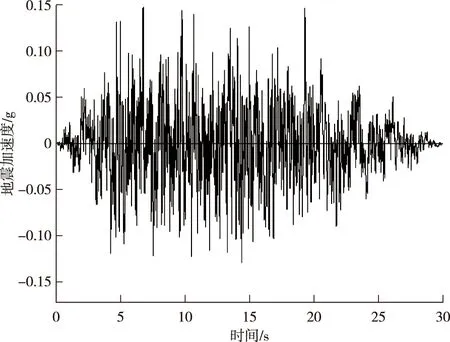
图2 地震波加速度时程曲线Fig.2 Duration curve of seismic acceleration

表2 邓肯-张E-B模型参数Table2 Duncan-Chang E-B model parameters
3 主要计算结果
3.1 静力计算结果
尾矿坝静力计算结果见图3~6。通过图3、图4应力等值线图可看出,尾矿坝的最大主应力和最小主应力均为负值,最大值出现在靠近坝基处。坝体无受拉区域,土体单元始终为受压状态。通过图5可得到,最大应力水平为0.84,其最大值出现在尾细砂与尾粉砂的交界处,最大值小于1,表明未出现剪切破坏。通过图6可得到,孔隙水压力为0的面为浸润面,等值线图可看出浸润线的逸出位置在初期坝坝脚,没有从堆积坝坝坡逸出,由于该初期坝属于透水坝,从坝脚逸出是符合实际的。综上,该尾矿坝坝体静力稳定。
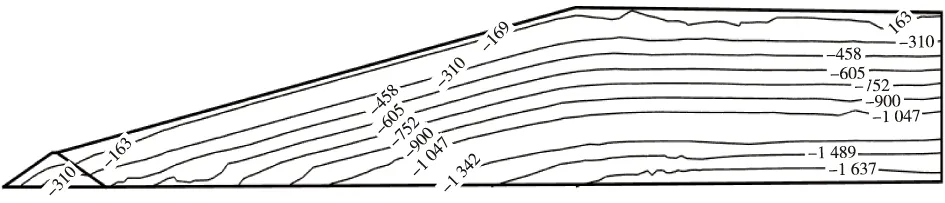
图3 最大主应力(单位:kPa)Fig.3 The maximum principal stress(unit:kPa)
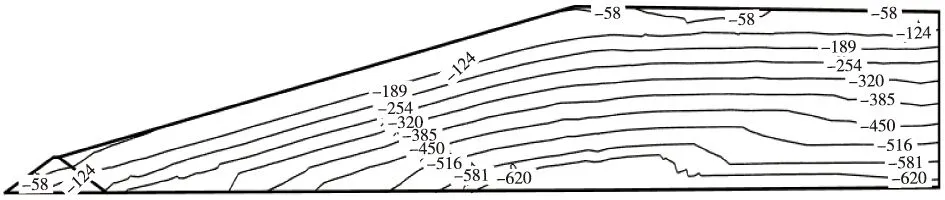
图4 最小主应力(单位:kPa)Fig.4 The minimum principal stress(unit:kPa)
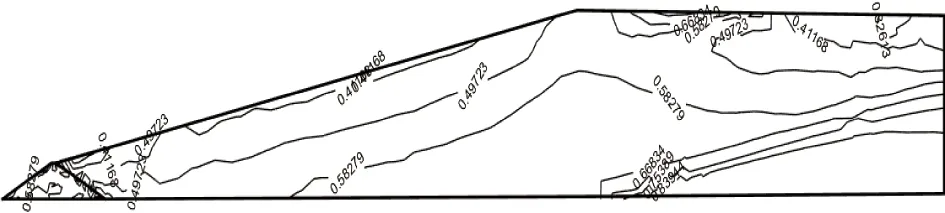
图5 坝体应力水平Fig.5 Stress level of dam body
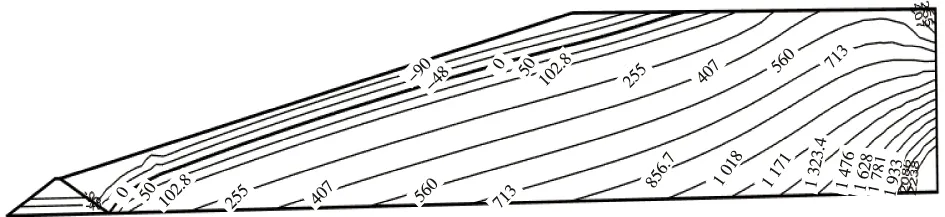
图6 孔隙水压力分布(单位:kPa)Fig.6 Pore water pressure distribution(unit:kPa)
3.2 动力响应分析
3.2.1 模态分析
本文开发的等效线性模型参数中,ω取结构的圆频率,因此首先对尾矿坝进行模态分析,提取坝体的频率,图7为尾矿坝第一阶振型(基本振型)图。
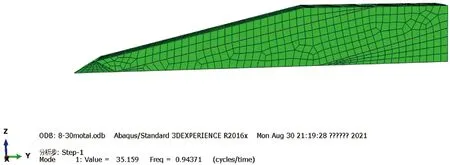
图7 尾矿坝第一阶振型(基本振型)图Fig.7 First order vibration pattern(basic vibration pattern)of tailings dam
尾矿坝坝体的自振频率计算结果如表4所示。

表4 坝体自振频率Table 4 Self-vibration frequency of dam body
研究表明:坝体动力响应的强弱并不完全取决于坝基地震的输入,还与坝体自身结构性质有关,坝体结构的自振频率和输入地震波频率越接近,说明坝体的动力反应越强烈。从表4中可以看出坝体的自振频率与输入地震波的频率相差较大,即坝体的动力响应不是很强烈。
3.2.2 动位移反应
坝体动位移反应如图8~9所示。堆积坝坝体水平向最大动位移0.47 m,垂直向最大动位移为0.037 m。堆积坝最大动位移均发生在坝顶附近,且从坝顶向下动位移逐渐减小。从动位移反应分布来看,水平向动位移相对垂直向动位移较大。
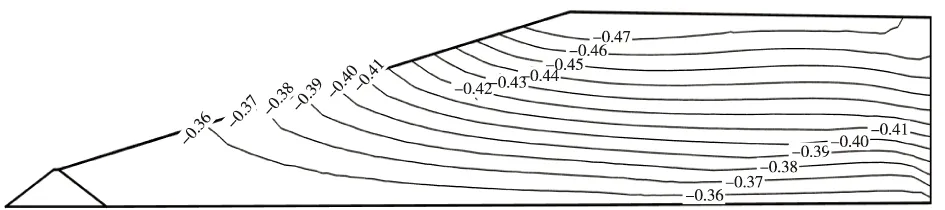
图8 水平向位移(单位:m)Fig.8 Horizontal displacement(unit:m)
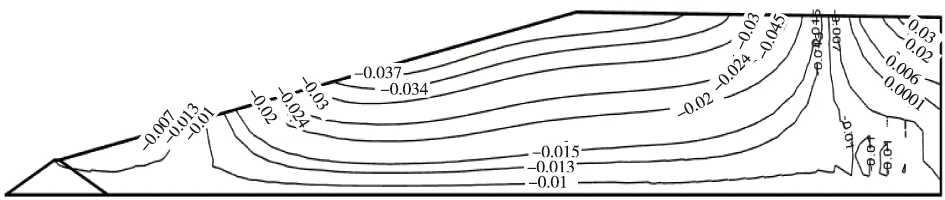
图9 垂直向位移(单位:m)Fig.9 Vertical displacement(unit:m)
3.2.3 加速度反应分析
垂直坝轴线中心剖面顺河向加速度等值线见图10,从图中可以看出水平向加速度分布不具有一定的规律,加速度最大值出现在干滩位置,最大加速度5 m/s2,相对于输入地震波峰值0.148 g,放大系数为3.38。
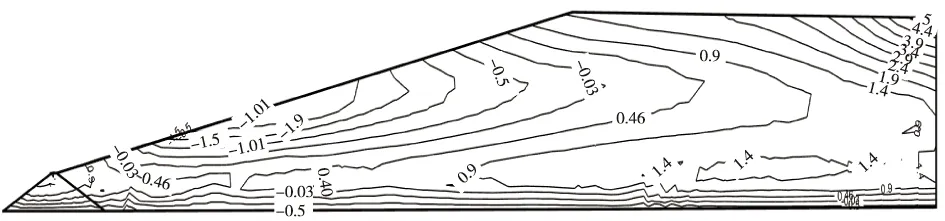
图10 中心剖面水平方向加速度等值线图Fig.10 Horizontal acceleration contour of central section
为了反映尾矿坝加速度随时间的变化趋势,通过计算得出中心截面初期坝坝顶节点、h/2坝高节点、3h/4坝坡节点、堆积坝坝顶节点四个典型位置的顺河向加速度的时程曲线,如图11所示。
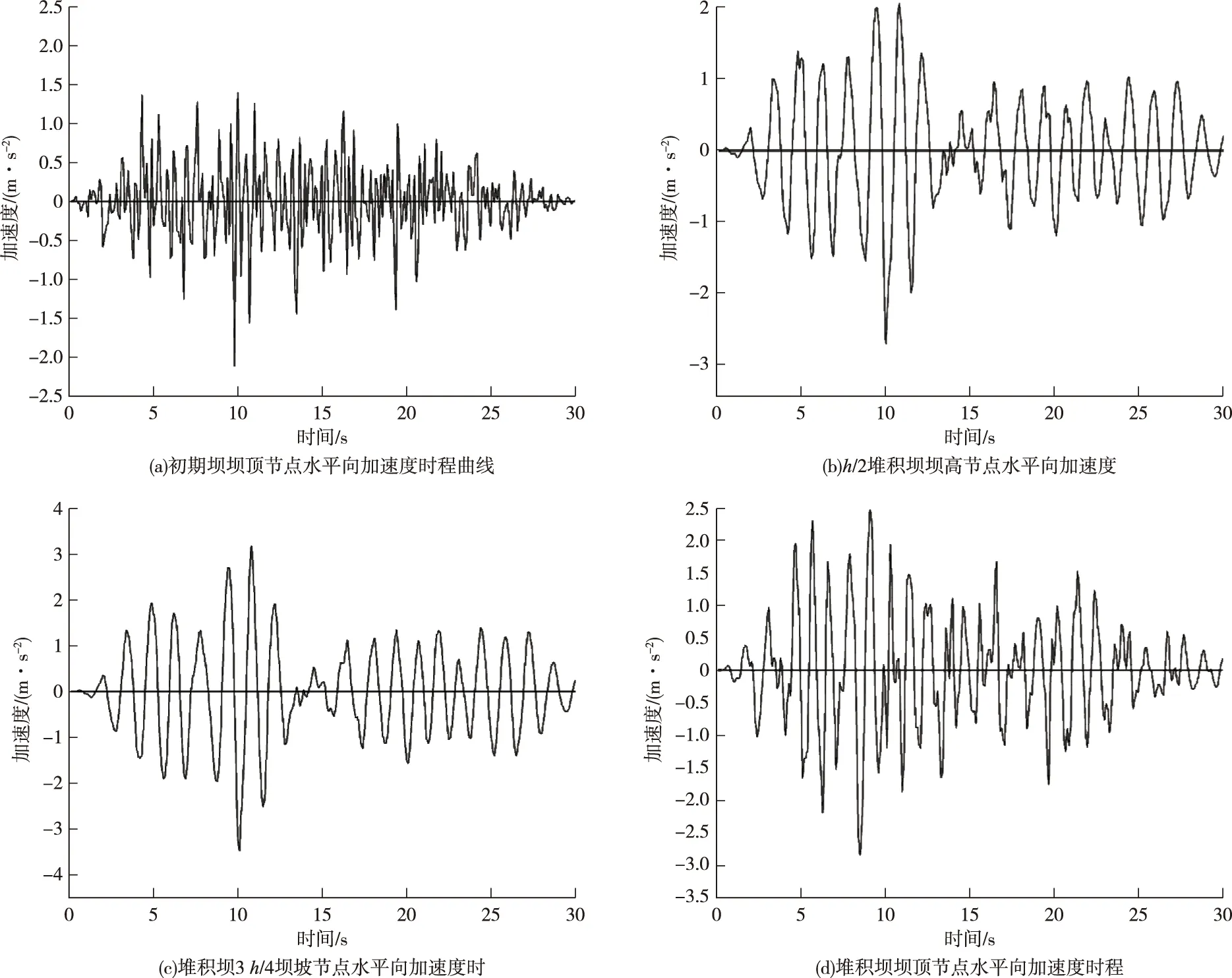
图11 加速度时程曲线Fig.11 Acceleration time history curve
由图11可以看出尾矿坝地震反应水平向最大加速度出现在5~10 s,即输入地震荷载历时的强震段,符合坝体受力的一般规律。初期坝坝顶节点最大值2.1 m/s2,放大系数为1.4;h/2坝高节点最大值2.7 m/s2,放大系数为1.8;3h/4坝高节点最大值3.4 m/s2,放大系数为2.2;堆积坝坝顶节点最大值2.8 m/s2,放大系数为1.89。其中最大值出现在3h/4坝高节点处,之后再往上加速度峰值有所减小。
3.2.4 动应力分析
尾矿坝体动应力反应如图12、13所示。从坝体中心剖面上动应力分布可知,堆积坝坝体最大动主应力为572 kPa,最小动主应力为260 kPa,动主应力分布均匀且全为压应力,最大动主应力和最小动主应力从上到下逐渐增大,极大值出现在坝基附近。
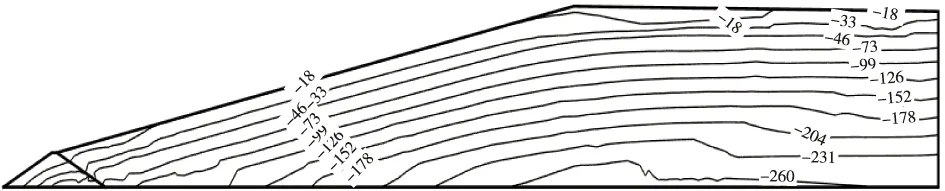
图12 最小主应力(单位:kPa)Fig.12 The minimum principal stress(unit:kPa)
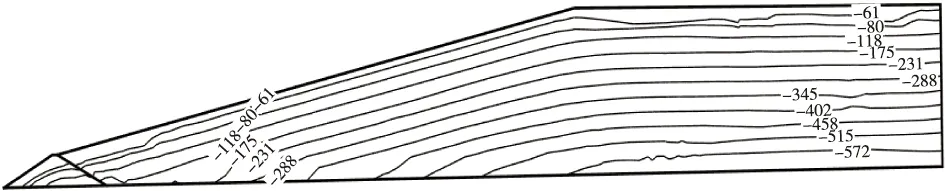
图13 最大主应力(单位:kPa)Fig.13 The maximum principal stress(unit:kPa)
3.2.5 地震液化分析
需要说明,在浸润线以上的区域为非饱和区,可直接判定为不液化,浸润线以下的区域通过孔隙水压力和震前平均应力的关系来判断。为了更加直观地观察尾矿坝是否发生液化及判断液化区域。本文基于FORTRAN语言编写孔压应力模型,计算地震过程中坝体单元的振动孔隙水压力。通过MATLAB语言编写后处理程序,生成不同地震时程下的坝体液化区域见图14所示。
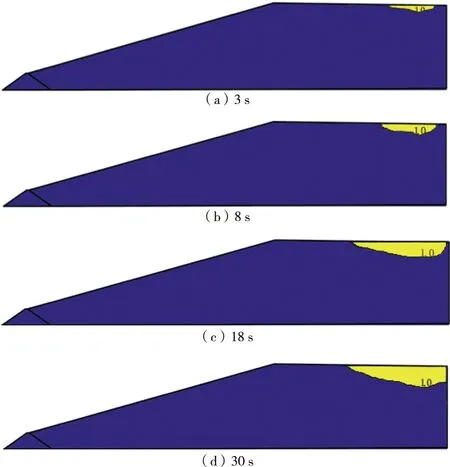
图14 不同时刻孔压比等值线云图 Fig.14 Contour cloud map of pore water pressure ratio at different times
为了更为直观地判断液化区域,图中只给出了ks≥1和ks<1的两个区域,图中可以看出黄色区域为液化区,蓝色区域为非液化区。液化结果显示:尾矿坝在地震发生3 s时局部发生液化,液化主要发生在上游积水浅层区域,其主要原因为上游积水浅层区域砂土处于饱和状态,上覆有效应力较其他区域小,在地震荷载作用下孔隙水压力在较短时间达到上覆有效应力,导致土体液化。0~18 s液化区随着地震时间的延长而增大,18~30 s液化区范围有小幅度的增加。综上所述,尾矿坝连续液化单元所形成的液化区主要集中在浸润线以下的沉积滩浅层区域,在坝顶和下游未出现明显的液化区域,且只在沉积滩区域出现小范围的液化,未形成滑移通道,但是小范围的液化区域也会对尾矿坝的稳定性造成不利影响。根据尾矿坝抗震灾害调查[10],尾矿坝沉积滩处尾矿料松散且长期处于饱和状态,在动荷载作用下容易发生液化,这表明本次计算结果合理。
4 结论
对尾矿坝进行静动力分析及坝体液化分析,得出以下结论:
1)静力分析计算得出最大主应力和最小主应力均为压应力,无拉应力出现;应力水平最大值为0.84,小于1表明未出现剪切破坏;浸润线逸出位置在初期坝坝脚,未从堆积坝坝坡逸出。故尾矿坝静力稳定。
2)在荷载作用下,坝体单元均处于受压状态;位移主要发生在坝顶附近和积水区域,顺河向最大位移0.47 m,垂直向最大位移0.037 m。坝体整体位移较小。四个典型位置在地震作用下加速度呈现相同的变化趋势,最大值均发生在强震阶段,垂直方向的振动相对水平方向反应较小,在该地震作用下反应不大。
3)尾矿坝在地震发生3 s时局部发生液化,液化主要发生在上游积水浅层区域,其主要原因在于上游积水浅层区域砂土处于饱和状态,上覆有效应力较其他区域小,在地震荷载作用下孔隙水压力在较短时间达到上覆有效应力,导致土体液化。0~18 s液化区随着地震时间的延长而增大,18~30 s液化区范围有小幅度的增加。该尾矿坝在地震时只出现小范围的液化,未形成滑移通道。

