基于深度DP搜索的穿越沙漠问题的研究

董正华 姜英姿 燕善俊

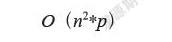
摘  要：针对特定游戏背景下穿越沙漠问题进行研究，从地图起点出发，以穿越沙漠为游戏背景在约定时间到达终点。在满足相关正负约束条件下合理利用初始资金使得到达终点时资金最多，游戏相关变量可分类为生存变量与收益变量。玩家需要在规定的负重范围内携带物资，若剩余物资不足以满足能耗要求则游戏结束。在路径最优方面，建立利用Dijskra算法实现剪枝的动态规划模型，并用C++编程求解，最后利用Lingo对结果进行检验，对促进多因素条件下路径的合理规划设计有重要意义。

关键词：动态规划;单源最短路算法;Dijskra算法;线性规划

中图分类号：TP311          文献标识码：A文章编号：2096-4706（2022）02-0111-03

Abstract： This paper studies the problem of crossing desert under the specific game background， starting from the starting point of the map， taking crossing desert as the game background and reaching the destination at the agreed time. Under the condition of satisfying the relevant positive and negative constraints， make rational use of the initial funds to maximize the funds at the end. The game related variables can be divided into survival variables and income variables. Players need to carry materials within the specified load range. If the remaining materials are not enough to meet the energy consumption requirements， the game ends. In terms of path optimization， a dynamic programming model of pruning using Dijskra algorithm is established and solved by C++ programming. Finally， lingo is used to test the results， which is of great significance to promote the rational planning and design of paths under the condition of multiple factors.

Keywords： dynamic programming; single source shortest path algorithm; Dijskra algorithm; linear programming

0  引  言

沙漠穿越問题创作思路源自2020年数学建模国赛B题，通过研究穿越沙漠游戏可得知其与TSP问题具有相似性，采用精确算法建立动态规划模型对本题进行求解。在相关变量的约束下建立状态转移方程，并通过动态规划对不同时间地点范围内的结果进行逐步寻优，最终得到使得耗费最小收益最大的可行方案。

动态规划模型重新定义问题与状态之间的联系，在满足后无效性的前提下，将主要问题分解为若干个子问题。本文在江苏省创新创业项目中通过记录子问题局部最优解来求取全局最优，在数学领域、物理层面的诸多工程技术上有着广泛的运用。

1  研究内容

从地图起点出发，以穿越沙漠为游戏背景选取不同路径在约定时间到终点。考虑到水、食物、到达终点的时间以及区域位置对问题产生影响，由此建立基于水、食物、到达终点的日期以及位置的动态规划模型。由于区域数量，携带水、食物的方案众多，需要对模型的空间限制和时限进行优化。利用Dijskra算法求取起点、村庄等关键区域的最短路径，缩小搜索范围。游戏中可能存在多个玩家，不同玩家为实现自身利益最大化，需考虑对手各种可能的行动方案。

2  全部条件已知时最优路径模型的求取

为研究穿越沙漠区域路线优化设计问题，对生存变量和收益变量进行约束同时兼顾总的收益最大目标，建立数学模型求解最优路径。

2.1  约束条件描述

假定穿越沙漠游戏中各区域内的天气情况事先已知，在保留的资金最多即消耗的水和食物的总价减去基础收益最小的情况下，求出一名玩家的最优路径。考虑到水、食物、到达终点的时间，以及区域位置对问题产生影响，由此建立基于消耗的水、食物、位置以及到达该位置的时间的动态规划模型。由于区域数量以及携带水、食物的方案众多，需要对模型的空间限制和时限进行优化[1]。

2.2  行进路线的选择

2.2.1  邻接矩阵的构建

游戏线路图中具有27个区域，两相邻区域间有一条弧，邻接矩阵中对应的元素为1;否则是0。特别的是，游戏规定可在本文域内选择停留，因此行程路线中存在自环，自环发生时的状态为1。按照邻接矩阵的定义，其邻接矩阵可以为：

单源最短路算法时间复杂度分析结果如表1所示。

2.2.2  行进中的假设

行进中起点、村庄、矿山、终点各节点变换过程中皆存在直达现象，为避免“绕路”现象的存在，对节点之间的路径采用Dijskra算法进行优化设计[2]，使得路程行进中花费的时间最短。

2.3  动态规划模型的建立

通过将穿越沙漠任务路程规划问题转化为多阶段决策问题，使用动态规划对该问题进行建模。主要依据游戏中生存变量和收益条件的要求作出约束条件，并由此建立各阶段间的状态转移方程：

2.3.1  停留休息花费代价的约束及转移方程的确定

21  return 运用公式（6），返回到达终点时资金最大值

通过算法1可以找到达终点时资金最大值，此时并没有输出最优路径，最优路径可以通过记录每个状态是由何种状态递推而来，确定路径是如何转移的。

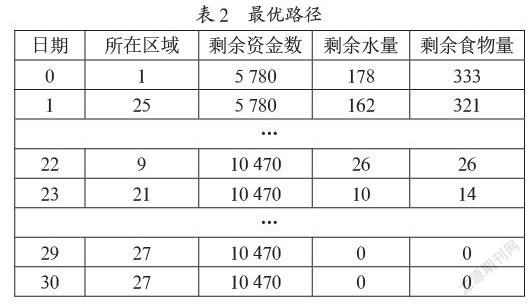
利用动态规划递推求解得出游戏结果，如表2所示。

2.5  Dijskra算法的优化

游戏路线中存在起点、村庄、矿山、终点四个关键节点，为实现收益最大化使用Dijskra算法对节点间路径进行规划。两点间路程选取与距离无关，与天气有关，可以看出途中存在大量的等效区域加大了运算的复杂度。

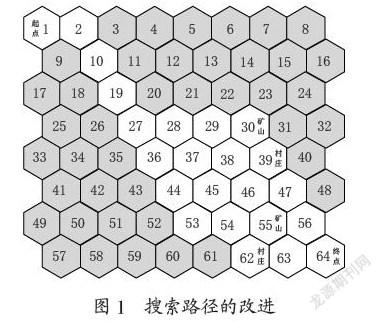
从沙漠区域图1中可以看出起点1、矿山30、村庄39、矿山55、村庄62、终点64之间直接到达路径的大致区域，选取这些点为研究对象（图中未加深区域）。

从图中可以看出，从起点经过矿山、村庄，最后到达终点的路径有多条。通过删除重复路径（图中阴影区域），降低了时间复杂度，极大了提高算法的运行效率，时间复杂度为：

O（n2*p）

3  模型的检验

首先，枚举每天的天气和路线，时间复杂度O（t！*3t）为然后利用线性规划理论[4]，在满足水、天气、挖矿收益等相关正负约束条件下合理利用初始资金使到达终点时资金最多。其中，游戏相关约束变量可分类为生存变量与收益变量。针对游戏地图问题，动态规划用于求解路径选取具有不可替代的优点，常通过记录子问题局部最优解来求取全局最优，因此可借助动态规划思想通过深度搜索若干可能情形进行求解。附录一中求出分别在第1天、第8天、第21天进行补给，运用LINGO对物资条件负荷量和需求量进行约束[5]，在此情况下求得收益函数最大。将所求结果与动态规划所求结果进行对比，验证结果的合理性，目标函数为：

运用LINGO求解得出最大收益分别为10 470，验证求解的结果正确性及模型的準确性。用线性规划求解时间过长，所以只是对确定路线和天气状态下水和食物的约束，验证了水和食物求解的正确性，总的时间复杂度为[6]：O（t！*3t*10002）。

4  结  论

本文的研究工作初步对沙漠穿越等多条件约束问题进行动态规划建模，而后建立动态规划模型对水，食物，到达终点的时间以及两个人分别所处的位置进行约束。利用Dijskra算法求得起点、村庄等关键区域的最短最优路径，使得行程中耗费最小。递归求解得出第24天到达终点时的剩余资金数为10 470，无剩余物资。并探究出了多条件约束问题在精确算法下的最优时间复杂度。

参考文献：

[1] 谢胜利，唐敏，董金祥.求解TSP问题的一种改进的遗传算法 [J].计算机工程与应用，2002（8）：58-60+245.

[2] 蔡之华，彭锦国，高伟，等.一种改进的求解TSP问题的演化算法 [J].计算机学报，2005（5）：823-828.

[3] 高海昌，冯博琴，朱利.智能优化算法求解TSP问题 [J].控制与决策，2006（3）：241-247+252.

[4] 周永权，黄正新等.求解TSP问题的离散型萤火虫群优化算法 [J].电子学报，2012，40（6）：1164-1170.

[5] 谢聪.求解TSP问题的改进离散蝴蝶优化算法 [J].数学的实践与认识，2020，50（1）：173-182.

[6] 贺亦甲，符强，朱俊杰，等.一种求解TSP问题的改进鸟群算法 [J].计算机时代，2019（5）：56-60.

作者简介：董正华（2001—），女，汉族，江苏盐城人，本科在读，研究方向：应用统计学;姜英姿（1970—），男，汉族，山东文登人，高级实验师，硕士，研究方向：数学与统计;通讯作者：燕善俊（1978—），男，汉族，江苏沛县人，副教授，硕士，研究方向：数学和信息科学。