基于机器视觉的轴承外圈表面图像拼接方法

赵春华， 贾玥泽， 谭金铃， 李香归

(1.三峡大学机械与动力学院， 宜昌 443002； 2.三峡大学水电机械设备设计与维护湖北省重点实验室， 宜昌 443002)

在实际加工过程中，生产出来的轴承不可避免地会存在一些表面缺陷，因此需要对生产线上的轴承进行表面质量检测。目前轴承质量仍主要由人工进行检测，但传统的人工检测有许多限制，如精确度低，工作强度高，受经验和主观因素影响大、需要更多人工投入、效率低等缺点[1]。以机器视觉为基础的检测技术现已取得长足进步，其无接触、无损伤、高速高效的优点弥补了人工检测的不足[2]。基于机器视觉的检测中，若要保证拍摄精度，则会受限于相机的焦距和物距，获得的单幅图像并不能涵盖整个轴承外圈表面的所有缺陷信息，通常会对一个目标轴承零件进行多次拍摄。在使用面阵CCD(charge coupled device)相机拍摄轴承外圈表面过程中，缺陷区域若位于图像边缘处，会导致单幅图片中的缺陷信息发生缺失，后续测量、缺陷识别会受到干扰[3]。为保证缺陷信息的完整性，必须进行图像拼接。轴承本身为圆柱体，其空间几何特性使得采集到的图像并不能真实反映轴承的空间信息。若不加处理直接进行拼接会使图像产生扭曲，发生严重的图像畸变，破坏轴承的实际视觉效果，不能体现其真实的空间尺寸和缺陷信息[4]。因此，必须按照一定的几何投影关系把采获的图片向同一平面映射，使图像中每个像素点和实际轴承保持对应，形成无差别的空间几何关系。在投影完成后再进行图像拼接，以获得包含实际空间位置关系和完整缺陷信息的图像。

图像预处理、配准、融合为轴承外圈表面图像拼接的3个主体环节[5]。从特征匹配算法的整体发展状态来看，具有旋转不变性和尺度不变性特征的尺度不变特征变换(scale-invariant feature transform，SIFT)[6]算法在图像拼接领域应用较为普遍。赵谦等[7]在工业管道内壁损伤检测中使用了该方法；陈月等[8]深入研究该法的应用，但其不足之处在于计算时间成本太大，需要较高的硬件配置，计算任务重，不符合实时性的要求；在多种特征检测技术分析和归纳的基础上，Bay等[9]提出了加速稳健特征算法(speeded-up robust features，SURF)，SURF算法配准效果好，并且其计算速度快三倍于SIFT。在图像融合领域，首照宇等[10]在平均融合法中加入了加权的思想，有效实现了图像无缝融合。

综上所述，虽然SURF算法已被广泛应用且发展较为完善，但在轴承外圈表面拼接领域仍未有过详细应用和说明。在前人研究的基础上，现使用面阵CCD相机作为图像采集设备拍摄轴承外圈表面，对获取到的图片进行拼接前的预处理和柱面投影变换，随后基于SURF算法进行图像配准，在引入加权平均融合算法后，即可无缝拼接图像。

1 图像采集及图像预处理

本文研究中设计的拼接方案分为4部分：图像采集和待拼接图像预处理、柱面投影、图像配准和图像融合，具体算法流程如图1所示。

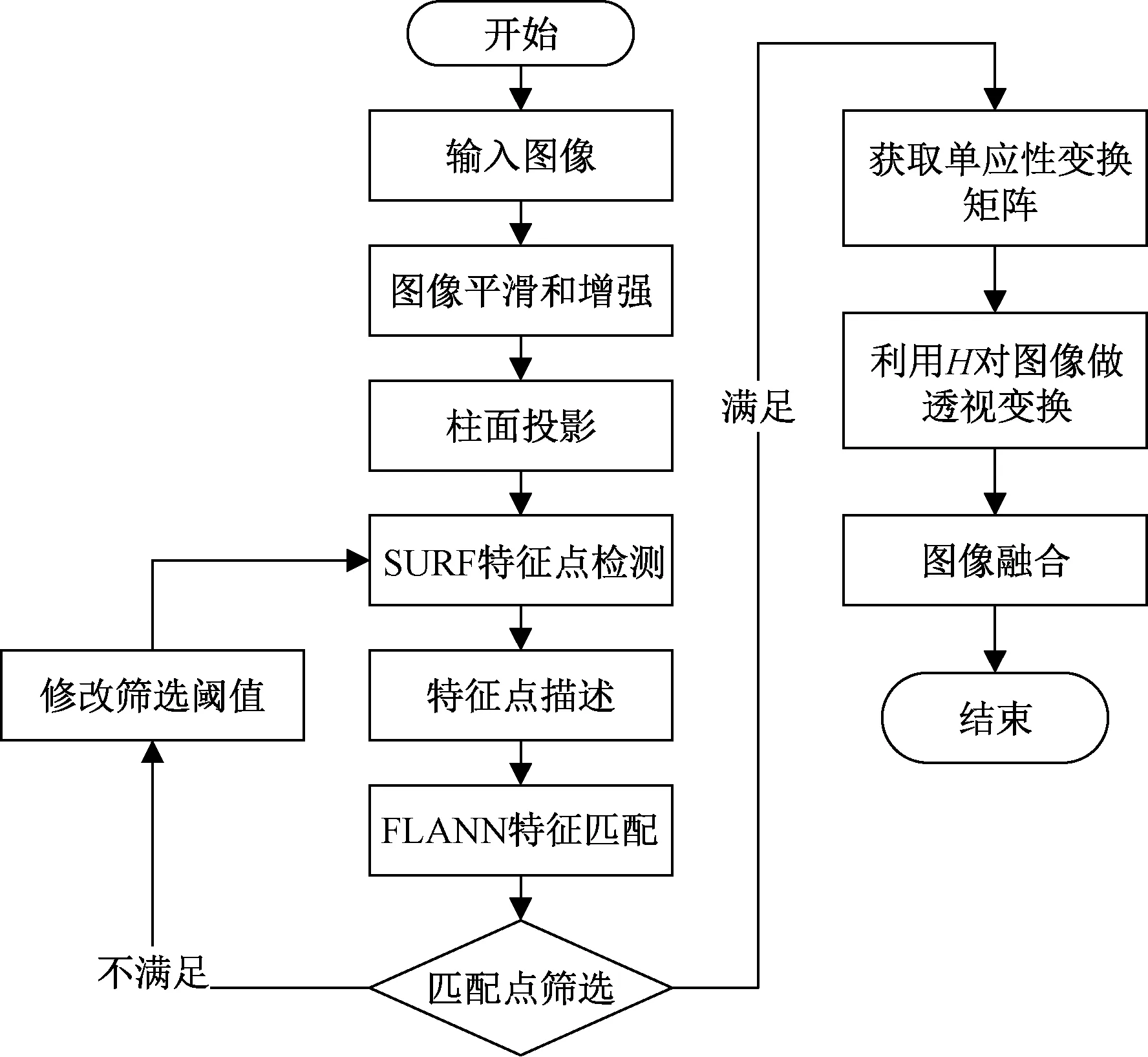
图1 拼接算法流程图Fig.1 Flow chart of stitching algorithm

1.1 图像采集

图像拼接的首要环节是图像采集，如图2所示。采用的是黑白面阵相机，型号为HikVision公司的MV-CE060。本实验采用环形LED光源照明，照明光源固定在相机镜头上，正面打光。轴承放置在实验平台上，每次旋转相同的角度，使相邻图像重合部分约为1/3，相机Z轴始终与拼接面垂直。为了确保本文所提的拼接方法对不同类型的缺陷图像均有效，实验数据选取具有代表性的3种轴承常见缺陷类型图片，分别为擦伤、磕碰和锈蚀，图片统一按照JPG格式行储存。

图2 图像采集设备Fig.2 Image acquisition equipment

1.2 待拼接图像预处理

在图像采集过程中，机器会存在震动、电路传输会造成信号波动等环境因素不可避免地会使采集到的图片产生噪声。而噪声点会影响特征点匹配的效果，也会给后续缺陷的分析和定位带来干扰。为把噪声剔除，需对轴承外圈表面图像进行滤波。

在实践和应用中，均值滤波、中值滤波、高斯滤波等是几种应用较为普遍的算法，中值滤波速度快，符合实时性的要求，并且对于小于一定尺寸的噪声点可以完全去除，对面积较大的噪声点也可以有效减少面积，同时在处理缺陷区域时能有效保留缺陷的纹理特征[11]。采用的降噪算法为中值滤波median，其原理公式为

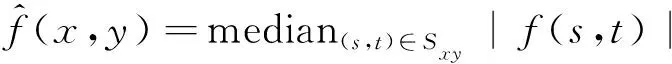
(1)

在图像增强领域中，大多采用直方图均衡化(histogram equalization,HE)作为图像预处理环节中对特征结构的增强。直方图均衡化可在整个直方图上分析亮度，一定程度上增强了局部对比度，且不会对图像整体对比度产生干扰[12]。其算法简单，无需借外因设置参数，运算速度快且效果较好，所以采用直方图均衡化实现图像增强。

2 图像柱面投影

轴承外圈表面为金属弧面，在采集到的图片中离图像中心距离越远的部位产生的图像畸变也越大。若不加以矫正，会导致图像边缘处的缺陷信息发生变形，在图像拼接时也难以使图片和实际轴承的空间约束保持一致。引入图像柱面投影原理[13]，对图像加以矫正，以便在进行拼接时得到空间约束和特征信息完整的图像。

图像柱面投影的关键主要在于投影变换公式，如图1所示，平面P是圆柱体Q的一部分，I是P展开后形成的对应平面。将图像运用柱面投影原理展开，即将圆柱图像P转换成平面I上的图像。

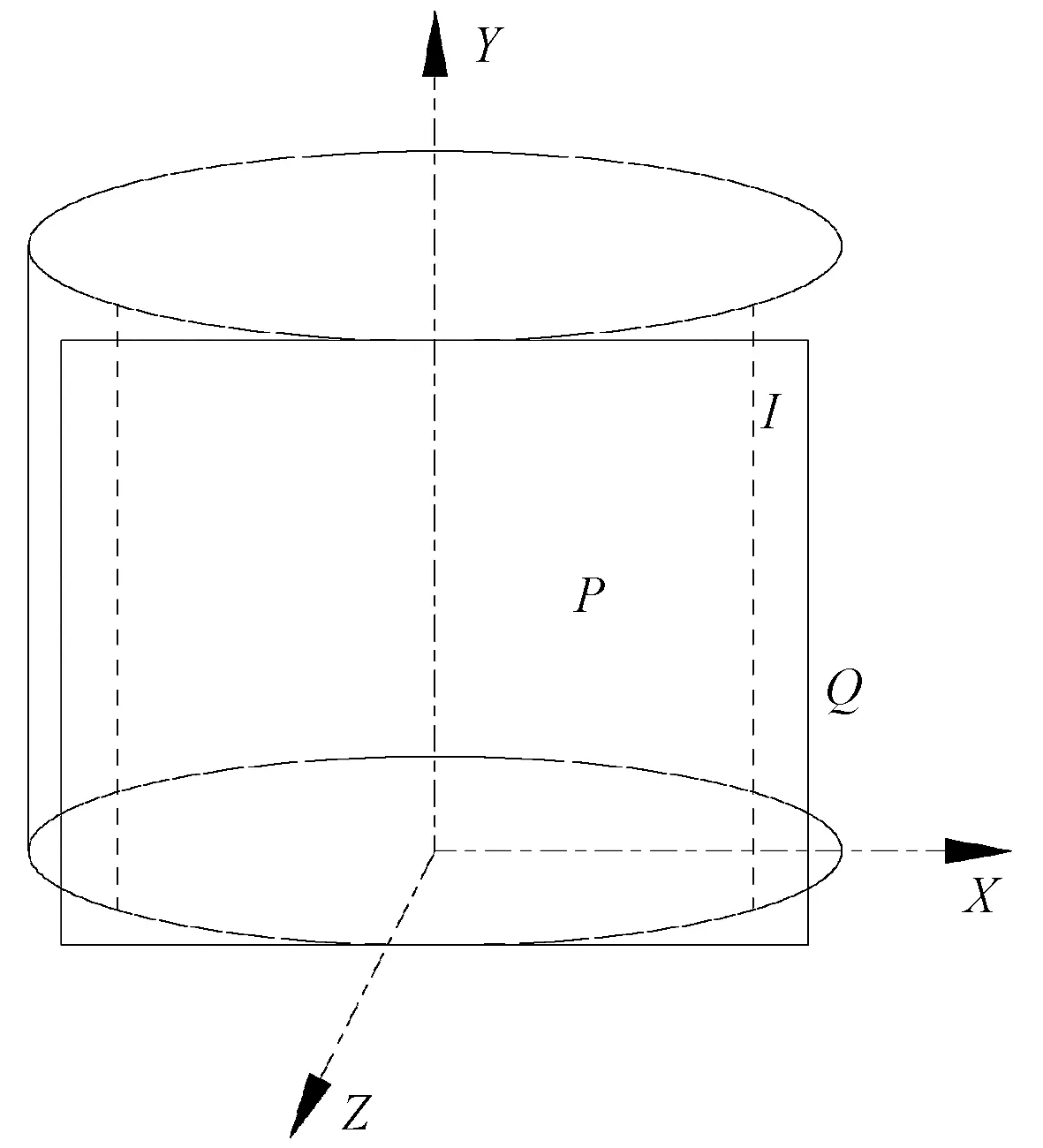
图3 柱面投影原理示意图Fig.3 The schematic diagram of cylindrical projection principle

图3中柱面P内任意一点L(x,y)由几何变换关系投影到平面I上对应的点K(x′,y′)，其变化关系可由图4和图5中的几何模型得到。任一水平方向(过点L)的截面如图4所示，图5为过点L与圆心连线的竖直方向的截面。

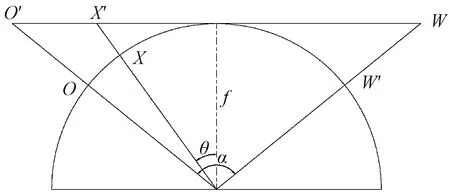
f为柱面半径；α为相机每次进行图像拍摄时对应的圆心角； θ为图像上任一点L和圆心连线与采集中心线的夹角；W为 原图像宽度；W′为投影图像宽度，H′为投影图像高度图4 柱面投影水平截面示意图Fig.4 The horizontal section diagram of cylindrical projection

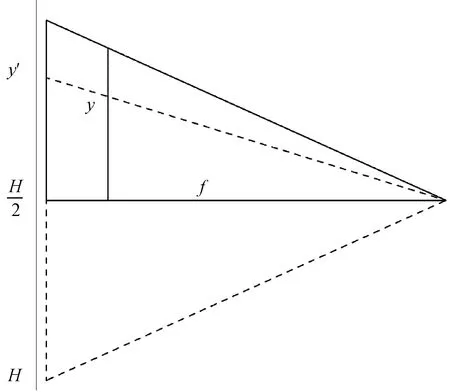
H为原图高度图5 柱面投影垂直截面示意图Fig.5 Vertical section of cylindrical projection

图4中，由几何关系可得水平坐标的映射关系：

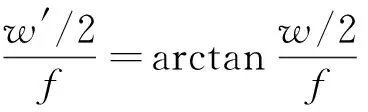
(2)

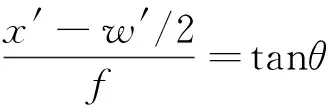
(3)

式(3)中：x′为投影图像横坐标；w′为投影图像宽度；f为柱面半径。

图5中，由相似三角形定理可得垂直坐标的映射关系：

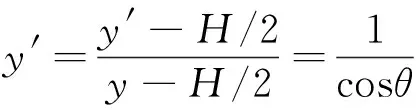
(4)

式(4)中：y′为投影图像纵坐标；y为原图像纵坐标。

L(x,y)投影至K(x′,y′)点(平面I中)的转换关系为

(5)

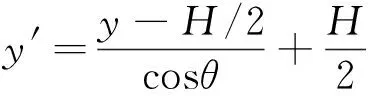
(6)

运用柱面投影原理可以一定程度的还原图像边缘区域的空间信息，对后续的图像拼接和缺陷检测具有重要意义。

3 图像拼接

3.1 图像配准

图像配准的基本步骤如下：提取经过预处理两幅图像的特征点，获得待匹配特征点；基于特定图像相似性度量寻找待拼接图像局部特征相似点对；以已匹配的特征相似点对为依据进行空间坐标变换矩阵的计算；最后以矩阵坐标变换为基础实现图像配准。采用加速稳健特征SURF算法进行特征点提取的具体流程为：依次构建积分图像、Hessian矩阵和尺度空间，定位、描述并匹配特征点。

3.1.1 建立积分图像

积分图像的构建应在特征点提取前完成[14]，积分图像思想的引入可以使SURF算法的计算量大大降低。对采集到原始灰度图像的像素坐标进行变换：从原始图像中左上角开始一直到某一点，两点之间所围成矩形区域内所有像素灰度值之和作为积分图像在该点的坐标值，且确保积分图像与原始图像无尺寸差异。积分图像原理示意图如图6所示，积分图像内建立坐标系，Y轴正向向下，X轴正向向右。

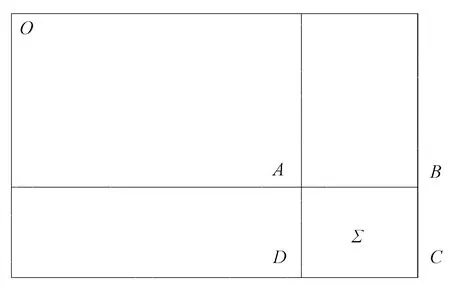
图6 积分图像原理示意图Fig.6 The schematic diagram of integral image principle

运用积分图像，可以把任意区域内像素和的累加简化为顶点坐标之间的加减，使算法整体运算量明显减少。图6中矩形区域ABCD中所有像素灰度值之和即4个坐标顶点的加减，灰度值之和Σ的计算公式为

Σ=C-B-D+A

(7)

3.1.2 构建Hessian矩阵

Hessian矩阵能有效检测图像局部特征的边缘信息，图像内各像素点对应的H[f(x,y)]为

(8)

该矩阵判别式为

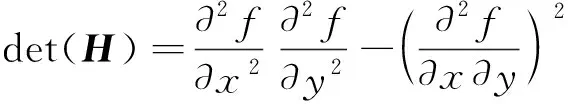
(9)

该矩阵特征值即为判别式的值。若图像中任一点的H判别式的值为局部极大值或者局部极小值，则该点为邻域内的极值点。

Hessian矩阵在图像中任一点(x,y)处尺度为σ的H(x,σ)的定义为

(10)

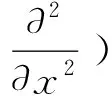
在Hessian矩阵构建之前还要进行高斯滤波，以确保获取到的特征点具备尺度不变性。但高斯滤波速度较慢，若把图像所有像素均进行滤波，则会大大拖慢算法运行速度。SURF采用盒式滤波器(Boxfilter)，以此替代高斯滤波器。在积分图像的基础上使用盒式滤波器，基本等同于先高斯滤波原始图像，然后展开Hessian矩阵计算。盒式滤波器和积分图像的使用把复杂冗余的运算简化为简单的加减问题，大大缩短了计算时间。高斯滤波器和盒式滤波器模板对比图如图7所示。

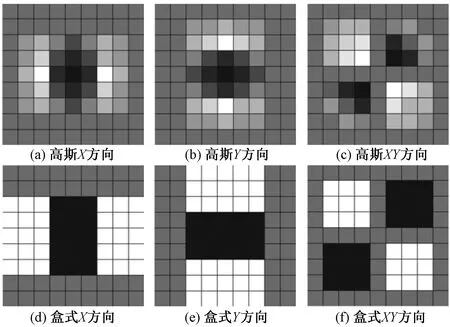
图7 高斯滤波器和盒式滤波器模板对比图Fig.7 Comparison of Gaussian filter and box filter template

滤波模板图7(a)～图7(c)分别为高斯滤波器X方向、Y方向、XY混合方向上的模板；图7(d)～图7(f)分别为盒式滤波器X方向、Y方向、XY混合方向上的模板，各类权重系数用颜色深度各不相同的网格表示。

Hessian矩阵行列式近似值为

det(H)=LxxLyy-(ωLxy)2

(11)

式(11)中：Lxx、Lxy和Lxy为图像在该点和盒式滤波器的二维卷积。引入加权系数ω(取经验值0.9)，以此消除因高斯滤波被盒式滤波器替代导致的偏差。

3.1.3 构建尺度空间

使用不同的尺寸模板，在所有尺寸模板下使用Hessian矩阵行列式近似值遍历图像中所有的像素点，形成该尺寸下的行列式图像。不同尺寸的行列式图像构成图像金字塔，也就是SURF的尺度空间。

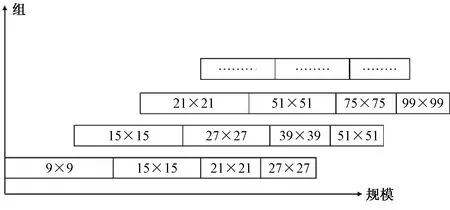
图8 尺度空间中盒子滤波器尺度分布图Fig.8 Scale distribution of box filter in scale space

3.1.4 特征点定位、描述与匹配

为定位目标特征点，每次选择SURF的尺度空间内的三层相邻行列式图像，随之对中间层各Hessian行列式的值进行比较。在以该点为中心的3×3×3邻域内，和余下26个像素点对比，确认该点是否为局部最大值或局部最小值点，做初步定位。除此之外，Hessian行列式的阈值同样需要设定，小于阈值的点剔除，高于阈值的点保留。

基于特征点方向的确定及其旋转不变属性的需要，要对其加以描述。以特征点为中心做(半径为6σ)圆。在该圆域内建立一个弧度为60°的扇形，可沿圆心转动。将扇形区域内所有像素的Haar小波特征(边长为4σ)进行计算，把水平方向和垂直方向的特征矢量进行累加，特征点主方向即为最大特征矢量方向。

以上步骤已经完成对图像特征点的提取与描述，随后应找出待拼接图像的局部相似点对，对其进行匹配。以欧氏距离为依据确定两个特征点是否匹配，分别求出特征点之间距离最近的两个点并计算比值，将比值与设定的阈值作比较，小于阈值则符合判定标准，反之则不符合。SURF还通过矩阵的迹来作为判别标准，若两个特征点矩阵的迹同号则符合，不同号则排除。为将错误匹配进一步减少，基于FLANN(快速近似最近邻搜索库)对提取到的特征点进行匹配，FLANN能够有效清除大部分错误匹配点，实现快速高效匹配。

3.1.5 图像透视变换

匹配的特征点对获取后，应对图像进行透视变换。通过求取单应性变换矩阵(homography matrix)对图像进行映射。3×3的单应性矩阵H表达式为

(12)

图像映射的前后关系式为

(13)

图像映射前任一对应点坐标(x,y)，映射后坐标(x′,y′)。经上述过程，图像配准已经完成，等待进行图像融合。

3.2 图像融合

轴承外圈表面图像拼接的最终环节是图像融合，将配准后的图像融合成一幅完整图像。

环境光线通常会对图像拍摄造成干扰，轴承不同角度和部位的图像之间往往存在着亮度的差异。本文研究中选择加权平均融合策略来完成图像融合的工作，为使图像重叠过渡区域像素变化更加平滑，降低亮度差异。加权平均融合原理公式为

I(x,y)=

(14)

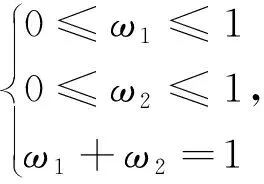
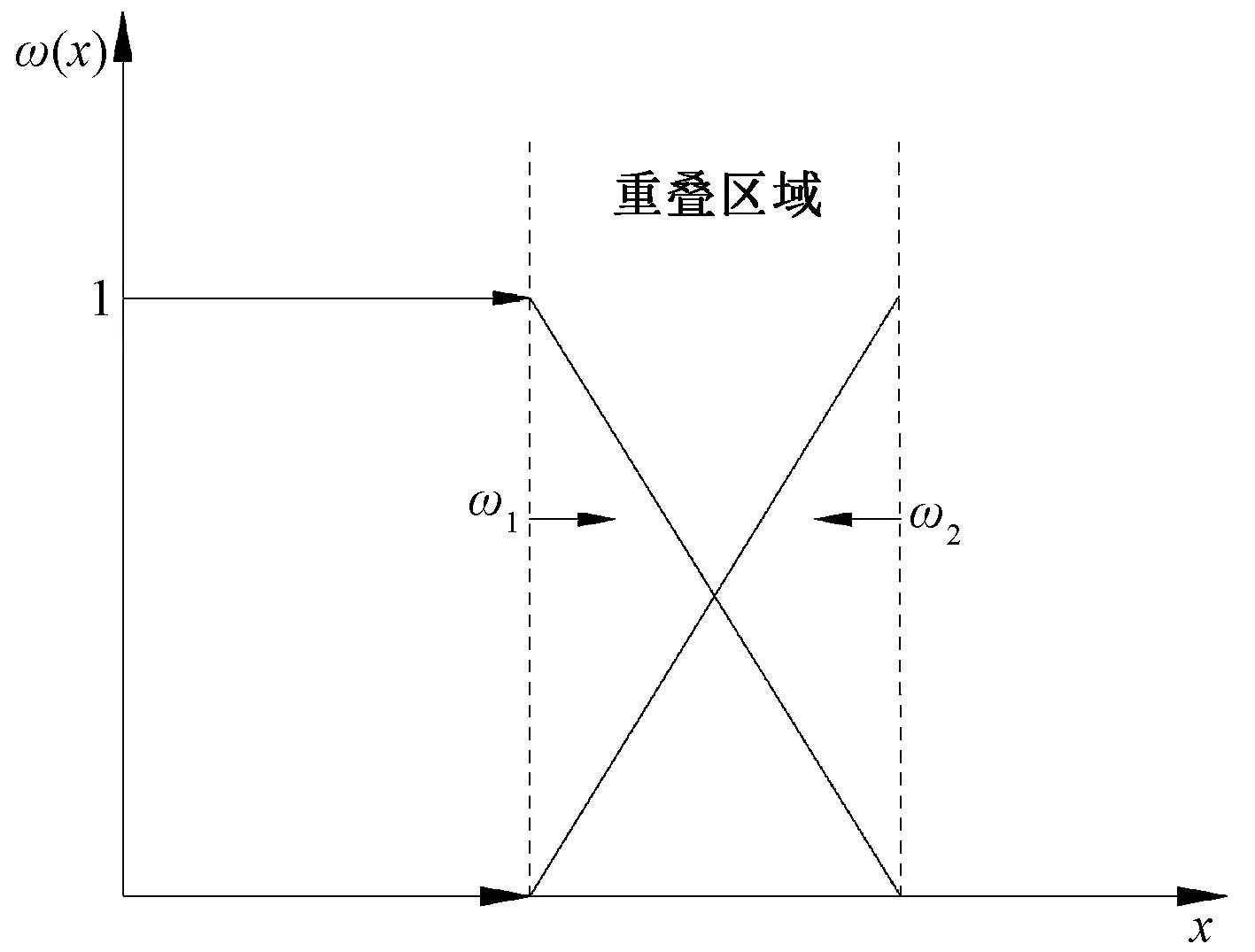
图9 加权融合原理图Fig.9 Weighted fusion principle graph

4 实验结果分析

4.1 实验过程与实验数据

本实验是在配置为Intel Core i5-9300H 2.40 GHz和8 GB RAM的个人计算机上进行实验与仿真，操作系统Windows 10，使用python语言编程，利用开源库OpneCV3.4.2为图像处理库。

将采集到的轴承外圈表面含有缺陷的图片进行筛选，挑选出需要进行拼接的图片。选择a、b、c3组分辨率640×480具有代表性的轴承外圈表面缺陷图像，故障类型分别为擦伤、磕碰和锈蚀，如图10所示。

3组不同缺陷的实验数据经预处理、柱面投影、图像拼接等流程处理后的完整拼接图像如图11所示。

图10 轴承外圈表面缺陷采样图像Fig.10 Sampling images of surface defects of bearing outer ring

图11 拼接结果Fig.11 Splicing results

4.2 评价指标

为验证柱面投影是否破坏了原图像信息、衡量图像是否失真，采用结构相似性(structural similarity,SSIM)作为评价标准。

(15)

式(15)中:μX为图像X的均值；μY为图像Y的均值；σX为图像X的方差；σY为图像Y的方差；σXY为图像X和Y的协方差。SIMM∈[0,1]，SIMM值的大小与图像失真程度呈负相关。

使用一种特征点匹配利用率来评价匹配的质量，以此确保能准确评价特征点匹配的质量。

(16)

引入峰值信噪比(peak signal to noise ratio,PSNR)[15-16]，通过计算图像噪声与有效信息二者之间的比例，以判断拼接后的图像的失真程度。PSNR的定义为

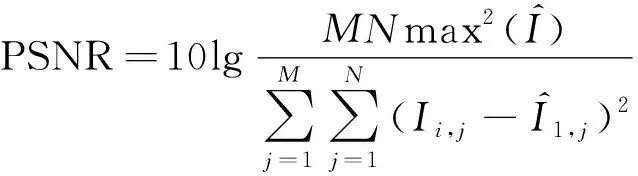
(17)

获取一幅完整的图像是图像拼接的目的，并且融合图像中应包含原图像中所有的特征信息。而轴承表面的缺陷区域包含大量的边缘特征信息，所以应采用一种从原图像传递到拼接图像的边缘信息量的计算方法作为质量评价标准。引入基于边缘信息保持度的客观评价指标，图像的边缘信息保持度(EPI)为

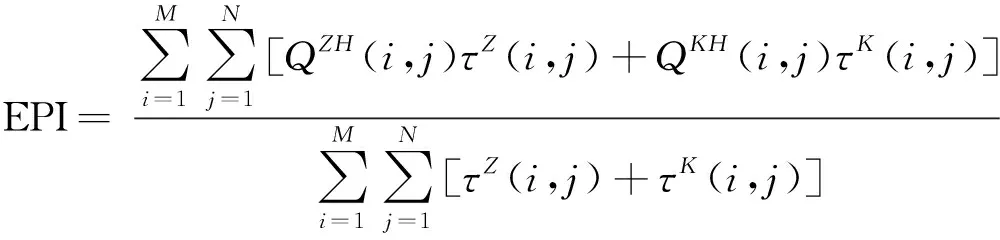
(18)

式(18)中：τZ(i,j)和τK(i,j)分别为QZH(i,j)和QKH(i,j)的权重；原图像边缘信息保持度为QZH(i,j)；拼接图像边缘信息保持度为QKH(i,j)。EPI取值为0～1，EPI值越高，表示边缘信息保留程度越大。人眼通常来说比较敏感于图像的边缘信息，所以使用EPI作为评价标准符合视觉检测的要求。使用PSNR和EPI两种指标相结合的方式来判定融合图像的质量是科学的。

4.3 图像融合质量对比实验

对采取柱面投影和未采取柱面投影的图像进行质量检测，来研究柱面投影是否会破环原图像的特征信息以致失真。表1为比较结果。

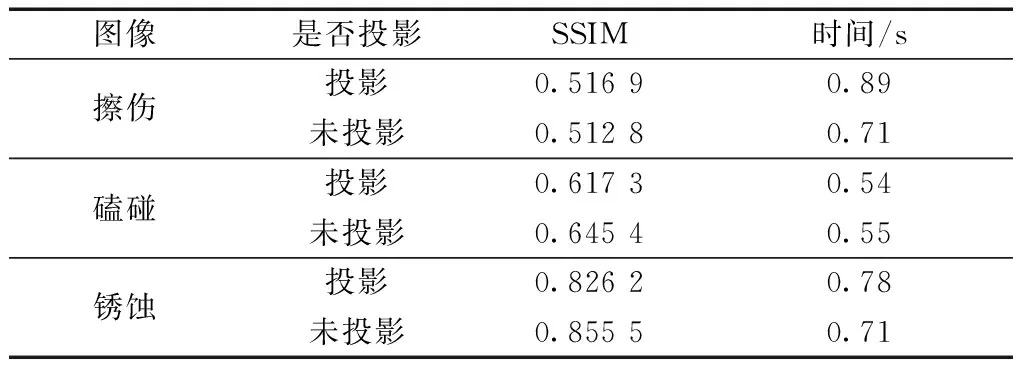
表1 柱面投影前后拼接质量对比表

由表1可知，未投影图像和投影图像的结构相似性相差很小，SSIM变化不超过5%；图像投影造成的时间消耗也可忽略不计。说明本文采取的柱面投影并不会破坏原图像的特征信息，也符合实时性的要求。

分别使用SURF算法与传统的SIFT算法对原始图像进行拼接，特征点的检测、匹配以及耗时情况具体结果如表2所示。

表2中数据表明，与SIFT算法相比，SURF算法提取和匹配数量更少的特征点，但SIFT算法特征匹配的精确度不如SURF算法，且SURF算法的时间成本更低。所以我们选择SURF算法作为轴承外圈缺陷图像配准的方法。

融合图像的PSNR和EPI结果如表3所示。

由表3可知，经过SURF算法处理后，图像的峰值信噪比和融合图像的边缘信息保持度基本上都是要高于SIFT算法，说明SURF算法的图像质量更加稳定，原图像的特征信息保留的也更加完整。

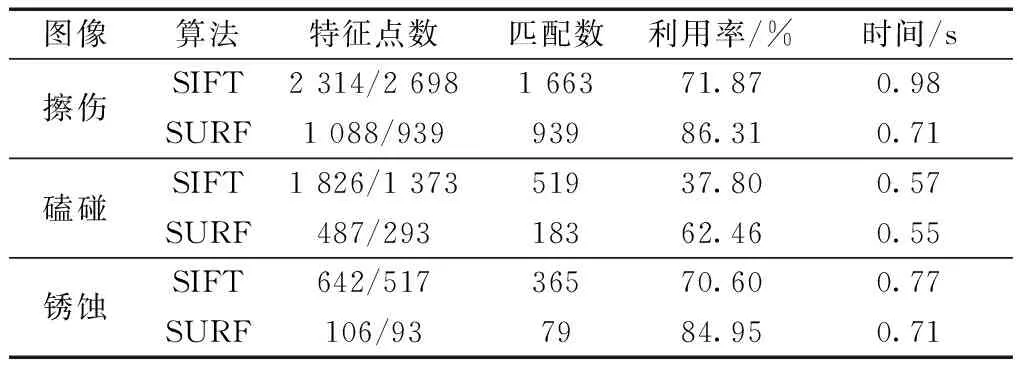
表2 基于SIFT算法和SURF算法的图像拼接比较

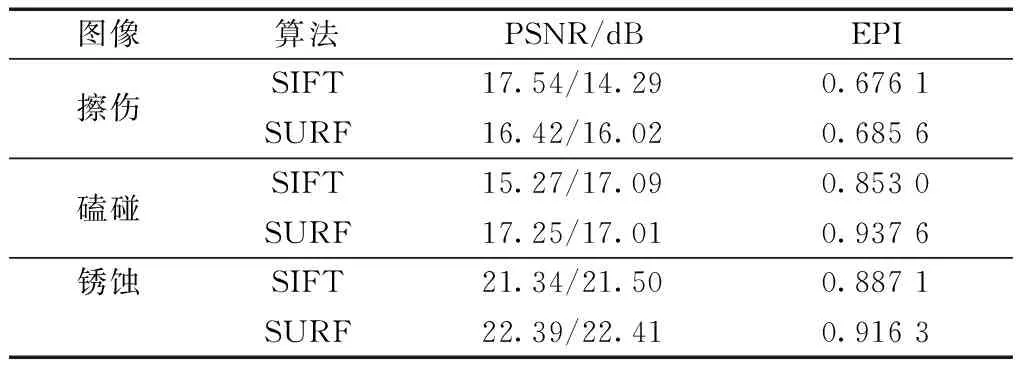
表3 基于SIFT算法和SURF算法的融合质量对比

5 结论

本文研究中所用拼接方法是在已有拼接方法的基础上，将柱面投影原理与SURF特征点检测算法相结合，还原图像边界区域真实的空间位置信息；运用SURF算法建立Hessian矩阵和尺度空间进行特征点的提取、描述和匹配；以FLANN为基础搜索匹配结果，将错误匹配点剔出；最后利用加权平均融合算法实现对轴承外圈表面图像的无缝拼接。

实验结果表明，本文所提方法可恢复轴承外圈表面图像的真实空间位置关系，将缺陷区域的特征信息有效保留，对边缘具有不完整缺陷区域的轴承图像实现有效拼接，为图像的准确性及拼接质量提供有效保障。其理论与实践意义较为明显。