盾构隧道开挖面稳定性数值模拟研究综述

张世民， 舒营， 尹鑫晟， 杨桦， 宋翔

（1.安徽理工大学土木建筑学院，安徽 淮南 232001；2.浙大城市学院土木工程系，杭州 310015；3.浙江省建设工程质量检验站有限公司，杭州 310000）

0 引言

随着我国城市化进程的加快及城市人口的激增，以铁路为代表的城市轨道交通建设量显著增长。据统计2016～2019年，轨道交通年均新增里程达628km，年均增长率为15.25%，可以看出中国城市地下空间发展之迅速［1］。盾构法凭借自身优势成为城市地下施工的主要手段，其中土压平衡式盾构目前在国内使用较为普遍。伴随地下空间“中国速度”，各类地下空间事故与灾害发生频次大幅增长。据统计2018年10月～2021年8月国内地下管线相关事故总数每年增加约600起，其中由开挖面失稳引起的安全事故约占地下管线事故总数的25%，总伤亡由200人增加到337人。因此有必要总结分析开挖面稳定问题，采取措施降低事故发生频次。

通过对盾构施工事故案例的分析，盾构施工中引发的地面塌陷等事故，主要由开挖面失稳造成，特别是当盾构隧道在渗透性较大的地层施工遇到未勘明的情况时，开挖面出现失稳事故频率更高。据统计，2019年全省平均降水量比上年多18.9%，比多年平均降水量多21.6%［2］。我国受季风气候影响，降水量年内分配不均，多集中在夏季。受降雨影响的水位变化总体呈现上升趋势，会对开挖面稳定性造成负面影响。杭州作为沿海城市，极端天气下水位变化不仅受降雨的影响还受潮汐作用的影响。

目前研究开挖面稳定性的方法分为：理论分析方法、模型试验方法、数值模拟方法。其中主要理论分析方法有极限分析法和极限平衡法。模型试验方法也被广泛用于评估开挖面稳定性。相比理论分析方法和模型试验方法，数值模拟方法因其能处理复杂的土壤模型，预测隧道开挖过程中土壤和现有结构之间的相互作用，而被应用到隧道开挖面稳定性研究中。

1 数值模拟研究现状

1.1 数值模拟方法及理论

岩土工程界常用的数值分析方法有：有限差分法、有限元法、离散元法。有限元法以连续介质为出发点，而且往往基于小变形的假定，适合研究一般弹塑性问题。离散元法克服了连续介质方法的宏观连续性假设，从细观尺度研究非连续介质的力学行为，适合研究破碎岩石和大粒径砂岩、等不连续介质问题。有限差分法比较适合研究大变形条件下弹塑性问题，被越来越多的研究人员用于评价开挖面稳定性分析。其中有限差分软件FLAC3D被许多学者使用，意味着使用该软件可以获得良好的结果。

FLAC（Fast Lagrangian Analysis of Continua）由Itasca公司研发推出的连续介质力学分析软件。作为有限差分软件，相对于其他有限元软件，在算法上具有优点：①采用“混合离散法”，使模型更接近实际情况，结果更加准确；②采用动态方程，使模拟更准确；③采用显式解，花费时间少；④没有刚度矩阵存储，节省内存。满足盾构隧道开挖面稳定性分析对计算程序的要求。

在数值模拟方法中，本构模型对稳定性分析存在影响以及简单的本构模型有其局限性，因此本构模型的选择及其参数的确定尤为重要。

表1可以看出数值模拟中研究对象多为干砂和粘性土。粘聚力范围0～10kPa，内摩擦角在18°～30°，除Yin等均未考虑弹性模量随深度的变化。目前常用的是莫尔-库仑本构模型，这比试验观察到的表面沉降槽更浅和更宽［3］。因此有必要研究不同本构模型对开挖面稳定性的影响程度，以便选取更合适的本构模型做数值模拟分析。

表1 数值模拟本构模型选择

1.2 土体失稳形状与模式

开挖面失稳模式研究是制定防止开挖面破坏措施的前提。为了明确土体失稳破坏范围见图1，统计分析了前人研究中不同隧道埋深比C/D时失稳破坏范围。

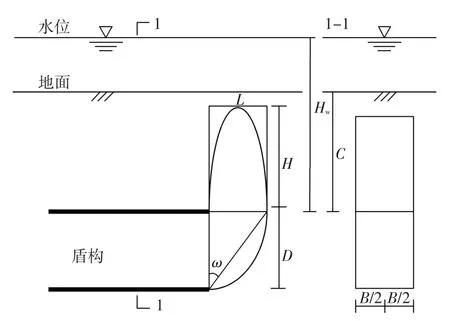
图1 开挖面失稳示意图

Chambon、Oblozinsky、汤旅军等［13-15］通过离心机试验，证明了埋深较小C/D=0.5时，破坏范围发展到地面；埋深较大C/D≥1时，土体破坏发展不到地面。破坏范围L=（0.26～0.5）D，H=（0.59～0.84）D。Chen、Takanod等［17，18］通过 1g模型试验，证明了C/D=2 时，破坏范围H=（1.18～1.5）D，由于地应力的影响，土拱效应没那么明显，土体破坏高度较大。因此，当隧道埋深比较大时（如C/D=1和2），“棱柱体”高宽比H/L=1.52～2.36，此时H/L的平均值约为2左右。也有学者通过数值模拟的方法获得了开挖面失稳破坏范围。由表2可知，埋深比较小C/D≤1时，土体破坏发展到地面。当埋深比较大C/D≥2时，土体破坏发展不到地面，破坏范围L=（0.35～1.33）D，H=（0.75～1.67）D。因此，隧道埋深比相对较大（如C/D=2）时，“棱柱体”高宽比H/L=1.2～1.78，此时H/L的平均值约为1.5左右。与模型试验的结果相比，除离散元的H/L与模型试验的接近，其他有限元和有限差分法的结果都比模型试验小，这可能与本构模型的选择有关，与Hejazi等结论一致。

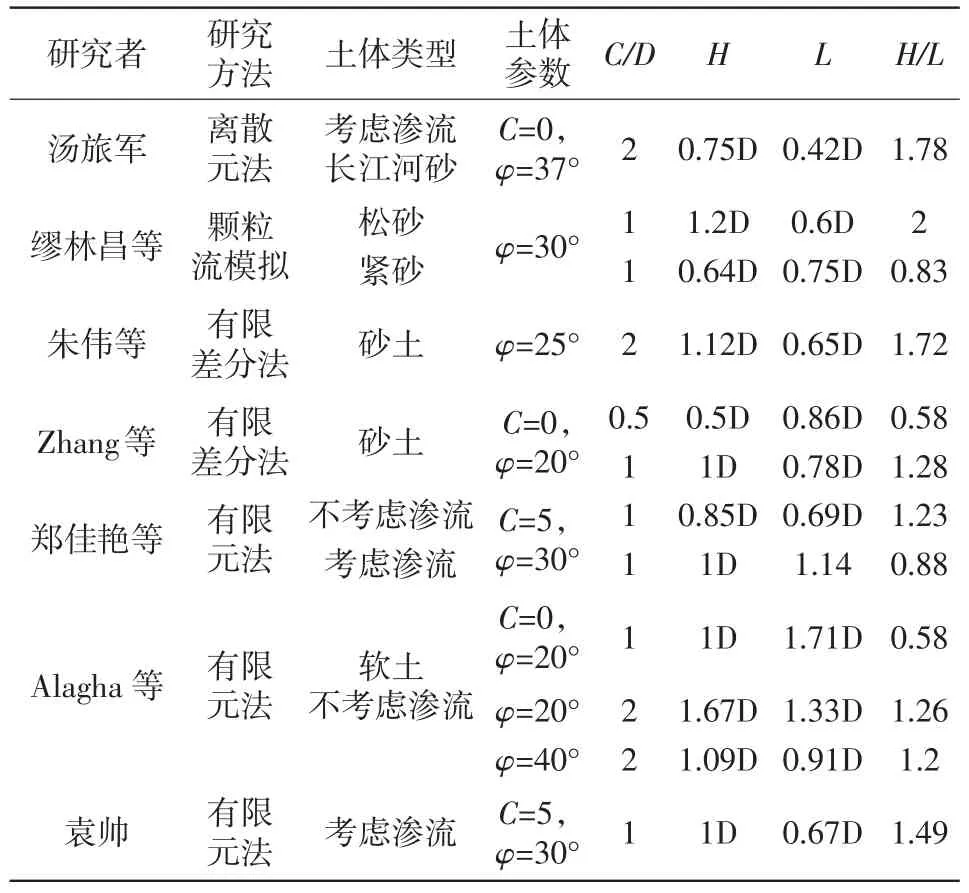
表2 盾构隧道开挖面失稳破坏范围

1.3 关于渗流的研究

前人已经用不同的方法研究渗流对开挖面稳定性的影响。Anagnistou等［22］通过三维稳态流动分析进行数值计算，他们提出了在几种水力边界条件下粘性摩擦土中所需有效支撑压力的评估列线图。有学者［23-25］应用Leca等［26］的上限解，使用数值渗流分析来确定渗透力。Buhan等［27］针对渗流力对土压平衡盾构隧道开挖面的影响，进行了三维有限元数值模拟，结果表明开挖面稳定系数主要取决于开挖面水平方向的渗透系数。有学者［28，29］得出有渗流情况下的极限支护力要比无渗流情况下大，而Yin等得出相反的结论。因此有待进一步研究出现分歧的原因。

表3中为前人研究的不同水位中的渗透力。其中Chen等［30］与Lee等的结果相似，这说明前者离心试验得到的隧道开挖面前方渗流场与后者的数值模拟结果基本一致。而Anagnostou等的渗透压力几乎是他们1.5倍，主要原因是他们不仅考虑了水平渗流压力，还考虑了竖向渗流力。Anagnostou等与黄皓［31］的结果相似，是因为后者从开挖面失稳破坏模式及极限平衡时的土拱效应出发，对考虑渗流的经典楔形体模型进行修正。楔形体上方的竖向力取决于开挖面失稳破坏模式及极限平衡时的土拱效应，作用于楔形体的渗透力取决于开挖面失稳破坏模式及开挖面附近总水头的分布情况。Perazzelli等的渗透力最小，一方面是不仅忽略了竖向渗透力的影响，还忽略了渗透力在x方向上的变化，另一方面是因为其最小值由条件V'（H）=Vsilo'确定，计算的是隧道顶部的值，因此会相比其他值偏小。

表3 渗透压力的比较

1.4 开挖面支护力的确定与分析

1.4.1 极限支护力的计算

目前，理论上主要采用Anagnostou等建立的“楔形体-棱柱体”极限平衡模型式（1）及Lee等提出的上限解式（2）来计算稳态渗流下开挖面极限有效支护力P′min。后来的学者大都在此基础上进行修正以确定开挖面极限支护力。

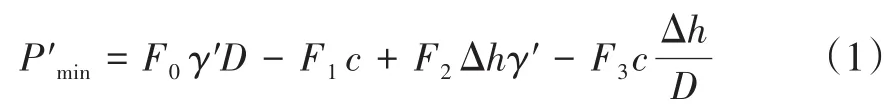
式中，γ'为土体有效重度；c为土体粘聚力；Δh为水头差；D为盾构直径；F0～F3为与摩擦角φ、隧道埋深比C/D、水深比Hw/D有关的无量纲量。

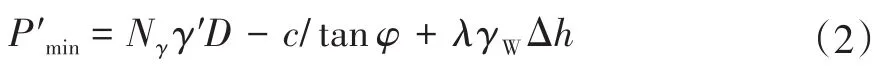
式中，λ为渗透力比值，Lee等建议近似取0.28；Nγ为与摩擦角φ、隧道埋深比C/D有关的无量纲量。

Alagha等用Midas-GTS NX进行三维有限元模拟，导出了一个新的方程式（3），计算在地下水位以上的纯摩擦土或c土的极限支护力。

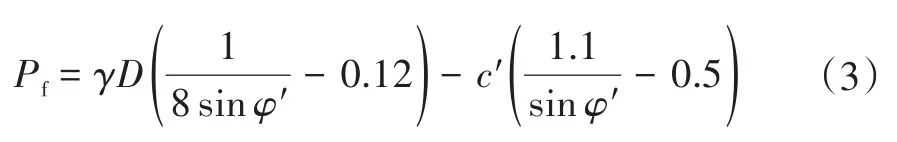
适用条件：①20°≤φ′≤40°，c≥0；②D≤10m，C/D≥0.5。

对比发现，理论分析得出的公式参数较多，而数值模拟得到的计算公式相对简洁，便于工程应用。

1.4.2 极限支护力的分析

为客观评价数值模拟方法得到的极限支护力的准确性，将数值模拟结果与理论方法、模型试验方法的结果进行对比分析见图2、图3。由图2可知，当隧道埋深比相对较小时，极限支护力随埋深比增大而增大；当隧道埋深比相对较大时，极限支护力受埋深比影响较小。离散元法、有限元法和有限差分法获得的极限支护力与经验公式预测的极限支护力较为接近。鉴于经验公式建立在大量精细有限元计算结果的基础上，因此该经验公式具有较高的可靠性，进而可以认为数值模拟方法得到的极限支护力准确性较好。其中，Anagnostou等的经典楔形体模型略高估了极限支护力。Krause［32］预测的极限支护力较为保守，这可能与其假定的开挖面破坏模式与实际存在较大差异有关。Chambon等的离心模型试验得到的极限支护力偏小，一方面是该试验中所用砂的内摩擦角φ=38°～42°略大于其他研究土体的内摩擦角，另一方面该试验所用的砂也具有微粘聚力c=0～5kPa。

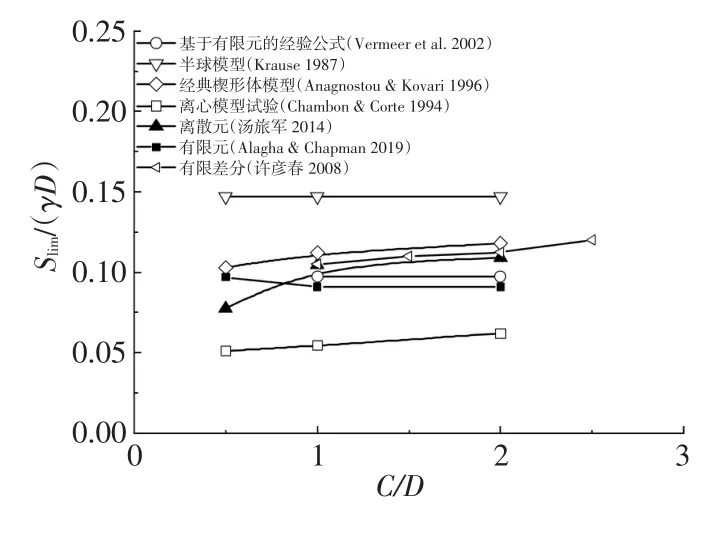
图2 开挖面极限支护力与隧道埋深比关系

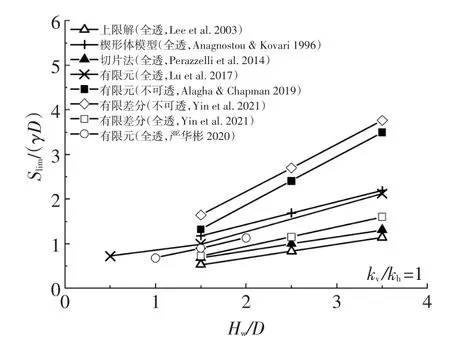
图3 开挖面极限支护力与隧道水深比关系

由图3可知，极限支护力随水深比的增大近似线性增大。当Hw/D为1.5～3.5时，开挖面全透情况下，Lee等计算的值最小，一方面是由于上限解计算出的极限支撑压力作为防止坍塌的保留荷载应该小于实际值；另一方面是低估了破坏区域的大小，忽略了竖向渗流力对破坏区域的影响。切片法的值小于数值模拟的值，这是由于在无限小切片中，滑动面面积方程不准确，对极限支护压力有较大影响，因此，切片法可能存在缺陷。Anagnostou等的值最大，因为他们提出的是计算最小支撑压力的极限平衡法，即下限解，下限估计应高于真实值。Lv等［33］的极限支护力大于其他数值模拟的结果，是因为其附加荷载为20kPa，γ'=7kPa/m，φ'=35°，c'=0，与其他数值模拟的参数存在差异。在开挖面全透条件下，严华彬的结果略大于Yin等的结果，可能是选择的数值模拟软件及土体参数存在差异造成的。在开挖面不可透条件下，Alagha等的值略小于Yin等数值模拟结果，是因为后者土壤比前者的更软，且前者的杨氏模量恒定为100MPa，而后者的杨氏模量取决于土体的应力，范围为0～57.3MPa。

综上所述，证明了数值模拟方法得到的极限支护力的可靠性。

2 不足及建议

通过文中分析可知开挖面稳定数值模拟研究中存在问题：①有对于稳态渗流的盾构开挖面稳定性分析的研究，但针对水位波动情况下的稳态渗流的盾构隧道开挖面稳定性分析还需做进一步的研究；②目前盾构开挖面稳定数值模拟研究中多假设土体为线弹性本构，本构模型的选用较为单一；③缺少通过数值模拟方法总结分析出的量化公式。针对以上问题可做如下考虑：利用数值模拟便于控制条件的优势，通过考虑渗透率等条件来实现水位波动的边界条件，进而实现非稳态渗流的工况模拟；可进一步考虑土体的塑性，在流固耦合研究中考虑更复杂的土体本构模型，选用更贴合土体特性的本构模型；考虑开挖过程中的应力释放等因素，对盾构隧道开挖面前方土体的位移以及破坏过程进行更精细的模拟，并通过大量的工况模拟总结出求解公式。

随着计算机技术的日趋成熟，数值模拟法越来越多的被应用到开挖面稳定性的研究，并取得显著成果。特别适当隧道开挖稳定性分析中边界条件复杂且地层材料不均匀时，数值模拟法更易于实现且结果易于整理分析。盾构隧道开挖面稳定性数值模拟的研究也会越来越精细化。

3 结语

文中通过总结国内外学者关于开挖面稳定性分析的研究成果，从数值模拟方法及理论、土体失稳模式、渗流作用及极限支护力的确定4个方面展开研究，得出以下结论：

（1）数值模拟对盾构开挖面稳定性研究对象多为干砂和黏性土。多选用莫尔-库伦本构模型，且弹性模量大多未考虑随深度的变化。证实了FLAC3D模拟盾构开挖面稳定性问题的可行性。

（2）通过对盾构开挖面失稳破坏范围的统计分析发现，除了离散元的H/L与模型试验的接近，有限元和有限差分方法的结果要比模型试验偏小。本构模型对失稳区域有影响。

（3）在强透水地层中，土体中的渗流力对开挖面的稳定有着较大的影响，结合土体的渗透性考虑开挖面水土作用耦合作用更为符合工程实际。

（4）通过对现有的计算开挖面极限支护压力的理论方法进行了评价。数值模拟方法可以作为分析开挖面稳定性问题的可靠替代方法。