回收旧集料评价及再生合成级配设计与检验

文凤友

（湖南国信建设集团股份有限公司，湖南 株洲 412000）

0 引言

沥青混合料材料在道路工程中大规模的建设带来了日益增长的养护任务［1，2］，道路工程中旧集料回收利用是循环发展、节能减排的有效手段［3］。原有道路中集料在服役期间由于车辆荷载等其他荷载的反复作用，导致集料颗粒出现不同程度的破碎，原混合料级配配比与初始设计配比出现较大变异，原设计级配配比已不能作为指导再生合成级配设计依据，需依据回收集料级配筛分结果进行重新配比设计。

1 旧集料评价及变异分析

1.1 旧集料评价

依托某就地热再生施工项目，按照规范结对项目RAP料进行抽提筛分试验，其集料筛分试验结果如表1所示。由表1和图1分析可知，旧集料级配曲线出现明显细化的现象，其中9.5、13.2mm筛孔的粗集料超出级配上限值，且0.075、0.15mm筛孔的细集料较大偏出配中值。这说明该级配在服役期间由于车辆荷载的长期作用导致其级配有一定程度的细化，还有部分集料细化可能与就地热再生铣刨有关。

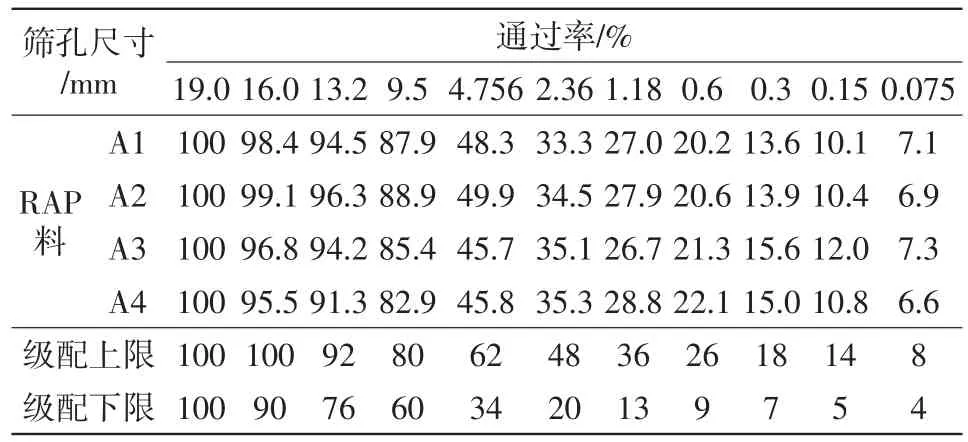
表1 RAP料筛分试验

图1 RAP料级配筛分结果

1.2 旧集料级配变异评价

旧集料变异主要来源于旧路面破损程度的差异与铣刨工艺造成取值样本间级配的变异［4］，而分析样本级配均匀程度常用方法为方差或标准差，若两者随机变量的方差相等时该方法则无法反映出两个随机变量各自的分散程度，而变异系数Cvi能反映某一变量自身的不稳定性［5］。故采用变异系数Cvi评估旧料级配的变异性。由于级配通过率是由各筛分计筛余量计算得到的，所以级配变异系数Cvi应采用分计筛余为基础进行计算，其计算公式：

式中，Pri为第i筛孔的分计筛余量，%；Pi+1为第i+1、i个筛孔的通过率，%；Cvi为第i筛孔的变异系数，%；Pv为第i筛孔分计筛余平均值，%。

由图2分析可知，13.2、16mm筛孔的粗集料其变异系数明显大于其他筛孔，说明16mm和13.2mm筛孔的变异性较大。0.075、2.36mm筛孔细集料比其他筛孔的细集料变异系数也较大，说明这两档细集料变异性较大。由图3分析可知，2.36mm筛孔的方差较大，说明该筛孔数据波动较大。

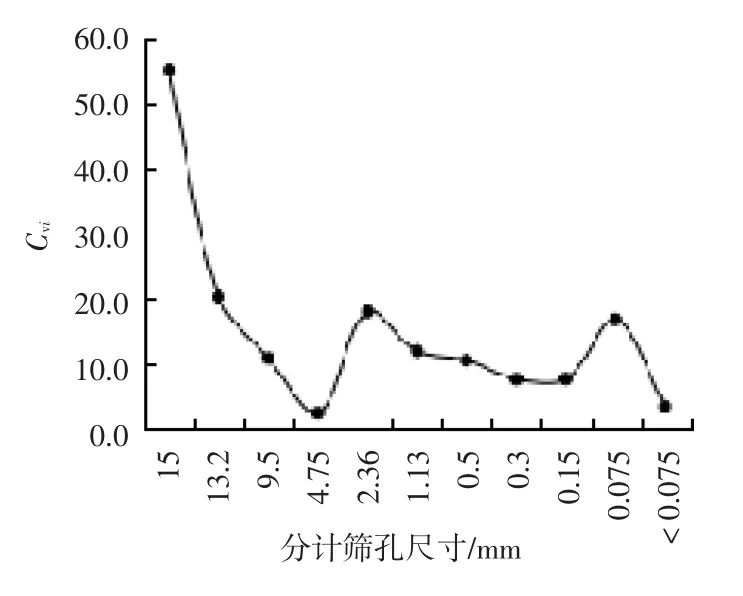
图2 变异系数Cvi变化示意图

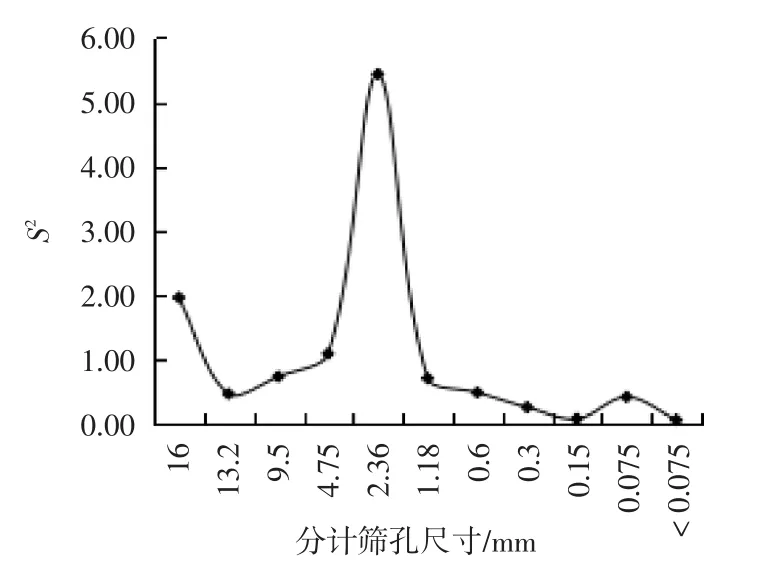
图3 方差S2变化示意图

由图4分析可知，16、2.36mm筛孔的变异性对旧集料整体的变异影响比较显著，其权重因子分别为14.62、24.32。同时，0.15mm＜0.075mm（筛底）筛孔细集料的变异性对整体变异性影响较小，其余筛孔的影响程度介于这两者之间。综合考虑级配离散性和权重明确了旧集料中变异性贡献主要筛孔为16、13.2、2.36mm和0.075mm。

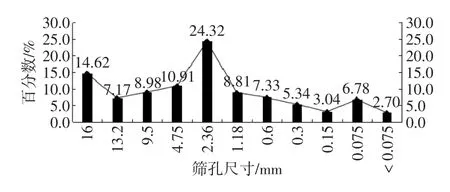
图4 各个筛孔权重因子

2 地热再生沥青混合料级配设计

2.1 表征细度模数合成级配设计

根据RAP料的级配类型是AC-16，选择新集料包括正大（13～16mm）碎石、正大（9～13mm）碎石、正大（6～9mm）碎石、正大（3～6mm）碎石、正大（0～3mm）碎石、2#机制砂、0.3#机制砂，填料为矿粉。

旧集料再生主要是旧集料级配的调整优化，通过加入一定比例新集料来改善其性能。以某就地热再生维修改造项目为依托，级配设计均采用该路面的RAP料。RAP掺量以60%、70%、80%比例进行再生料级配设计，为了合理控制旧料的变异性，选择超出级配上限最大的A2集料作为RAP料的代表级配，由于原旧料2.36mm筛孔通过率小于38%且9.5mm和13.2mm超出级配上限，目标级配以规范中值为参考结合旧集料特点设定为9.5mm以上筛孔略高于规范中值、4.75mm筛孔略低于规范中值的AC-16C型。

通过细度模数表征级配特点进行合成级配设计，该方法涵盖了0.15mm以上筛孔所有的孔径的通过率，对于级配特点有较为全面的反映。所以采用细度模数表征再生合成级配有一定的代表性。其计算公式如下：

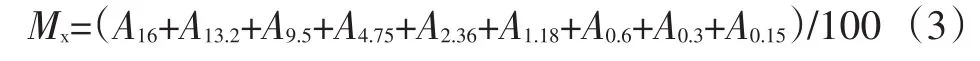
式中，Mx为细度模数；AX为各个筛孔累计筛余百分数，%。

在进行级配设计时为使不同RAP掺配比例的细度模数基本相同，对于不同RAP掺量采用不同的级配进行合成级配设计。通过对新集料级配不断的调试，各档集料筛分通过率及掺配比例分别见表2和表3，其合成级配如表4所示。

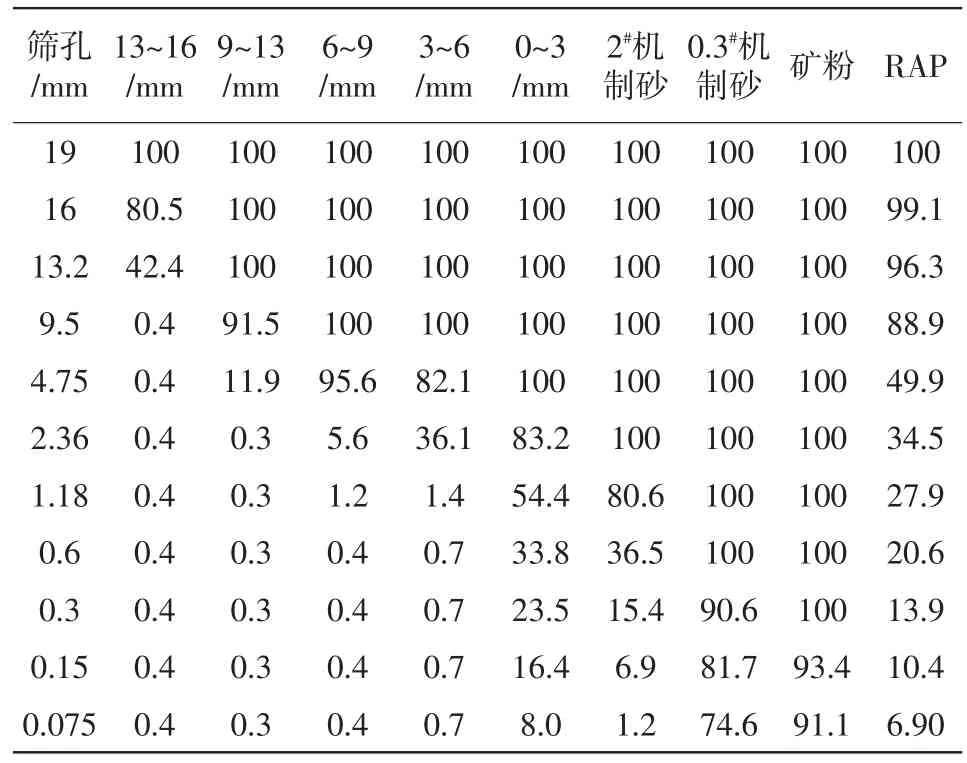
表2 各档集料筛分结果

表3 RAP料和各档料调用比例

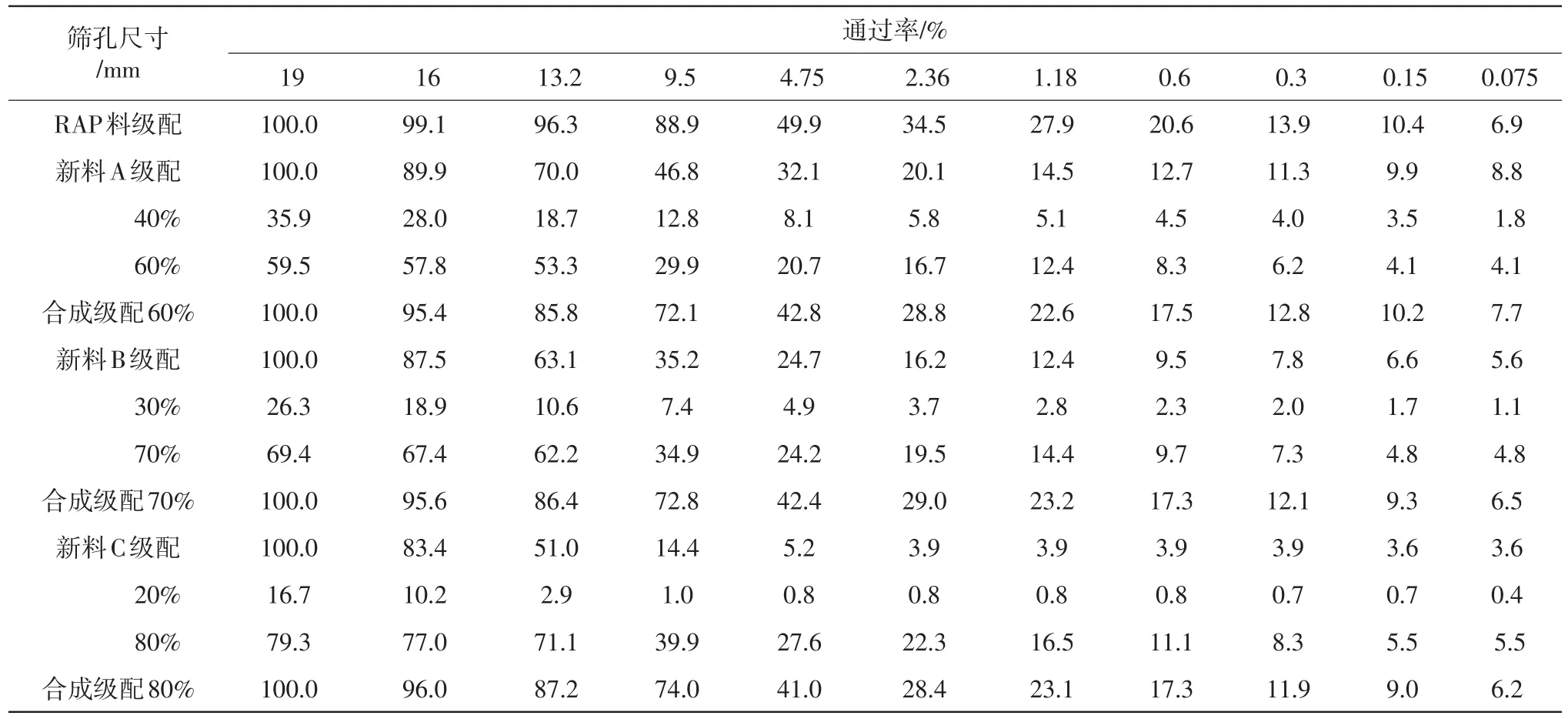
表4 各级配细度模数合成级配设计

由表3、图5分析可知，通过计算各级配的细度模数值基本相等，但80%RAP掺量的级配曲线仍稍偏离前两者。原因在于旧料掺配比例越大对其合成级配影响越发显著。新料级配A、B、C均不在AC-16级配范围内，RAP掺量越大其新料级配偏离级配下限值越大，虽其合成级配曲线基本重合。但其新料级配偏离AC-16级配范围的程度随着RAP掺量的增大而变大。故单从合成级配因素分析，RAP料掺配比例越大新料级配对旧料改善效应越差，偏离目标级配越大，导致可控变量因素增多。

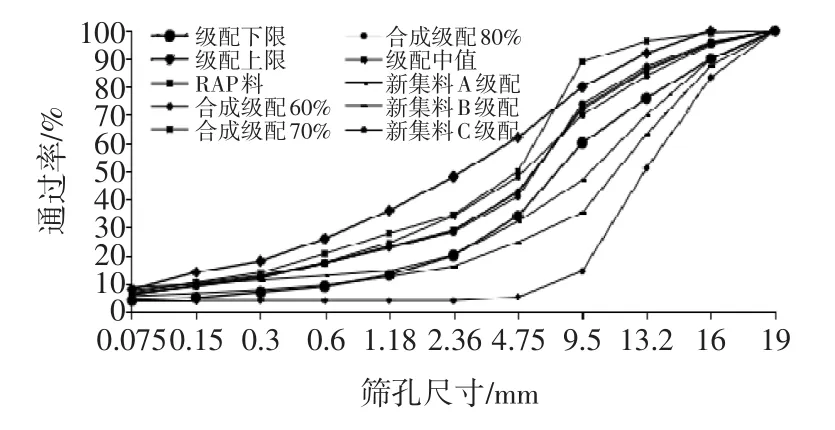
图5 细度模数合成级配设计

2.2 贝雷法检验

2.2.1 CA、FAc、FAf参数检验

对于非贝雷法设计的设计级配采用贝雷法［7］检验，一方面可以检验表征细度模数设计级配的合理性；另一方面能较好的反映出设计级配是否具有较好的粗细集料均匀性，其主体思想是采用CA、FAc、FAf这三个参数对合成级配进行分析。

（1）CA比。

式中，PD/2为D/2（D为公称最大粒径）的通过率，%；PPCS为第一控制筛孔的通过率，%。

（2）FAC比。

式中，PSCS为第二控制筛孔的通过率，%。

（3）FAf比。

式中，PTCS为第三控制筛孔的通过率，%。

上述关系中，比例因子采用0.22，PCS=0.22NMPS（NMPS为最大粒径）、SCS=PCS×0.22、TCS=SCS×0.22。参数统计结果见表5。

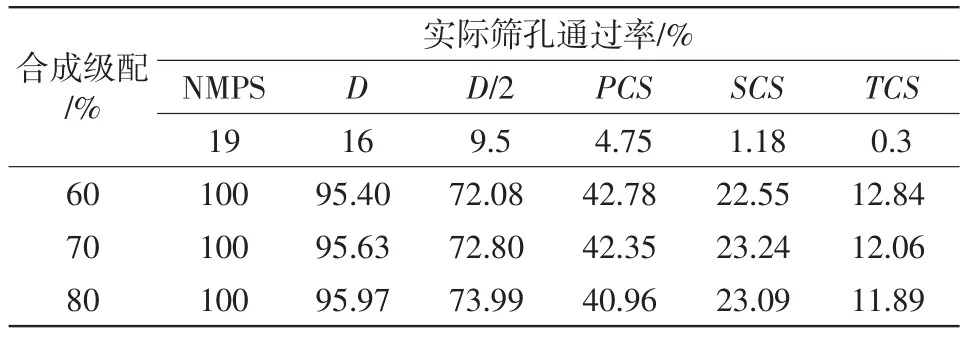
表5 参数统计

一般认为当CA比增大，D/2～PCS间的粗集料增多降低了集料压密性，而FAc比增大会导致空隙率和矿料间隙率变小，FAf则表示最细集料的嵌挤情况。由图6分析可知，掺量60%、70%和80%的合成级配其CA比均大于1，反映该级配粗集料较小粒径颗粒会悬浮在骨架结构中。而FAc和FAf均接近0.5，反映合成级配细集料均衡性较好。

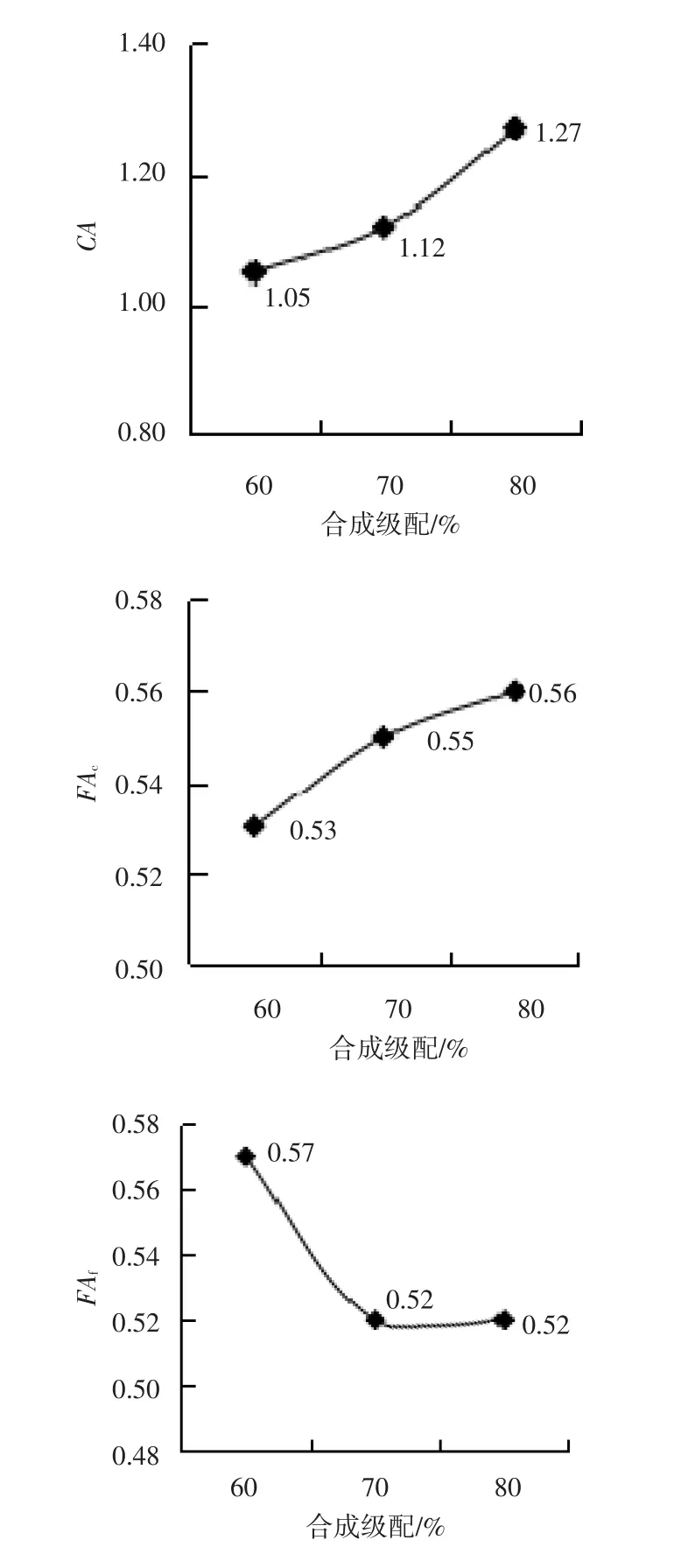
图6 合成级配掺量与检验参数关系

2.2.2 P理论筛孔修正

由以上3个参数可知，控制筛孔的尺寸并非是按0.22系数理论计算得到筛孔尺寸取值，而是按其接近筛孔尺寸的通过率来计算得到的，影响CA值的两个控制筛孔的理论值与实际值有较大差别［8］。因此，采用P理论筛孔（理论筛孔通过率）进行修正。理论筛孔的通过率值利用实际筛孔通过率的加权平均方法来计算得到。例P5.2=P4.75+（5.2-4.75）/（9.5-4.75）·（P9.5-P4.75），其计算结果见表6。

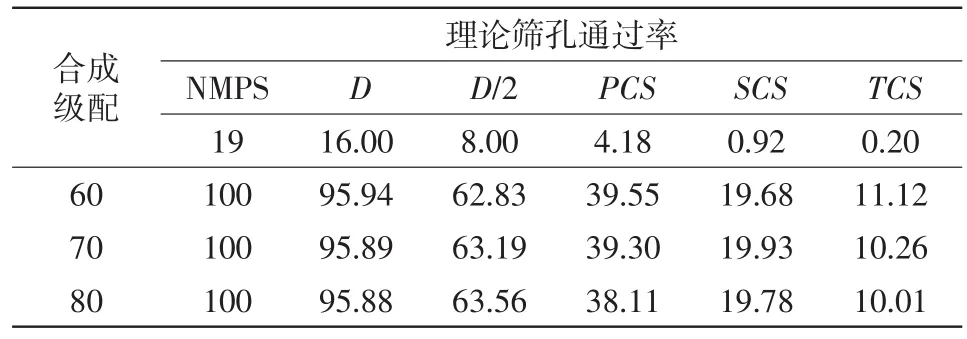
表6 理论筛孔参数计算结果%

由图7分析可知，修正后的CA值有较大的变化且比修正前明显变小，而FAc和FAf的修正前后变化较小。说明采用理论值临近的实际筛孔通过率来计算，对CA值影响较大。分析其原因在于13.2、9.5mm和4.75mm这3个实际筛孔之间孔径差值分别为3.7mm和4.75mm，可见第一控制筛孔的通过率其理论值与实际值会有较大的误差，使CA值出现明显变化。而修正后的参数除60%掺量FAf略大于0.55外，其余数值基本满足我国AC级配（CA比0.45～0.85、FAc比0.40～0.55、FAf比0.40～0.55）合理范围内，说明该合成级配粗细集料颗粒间较好的均匀性。

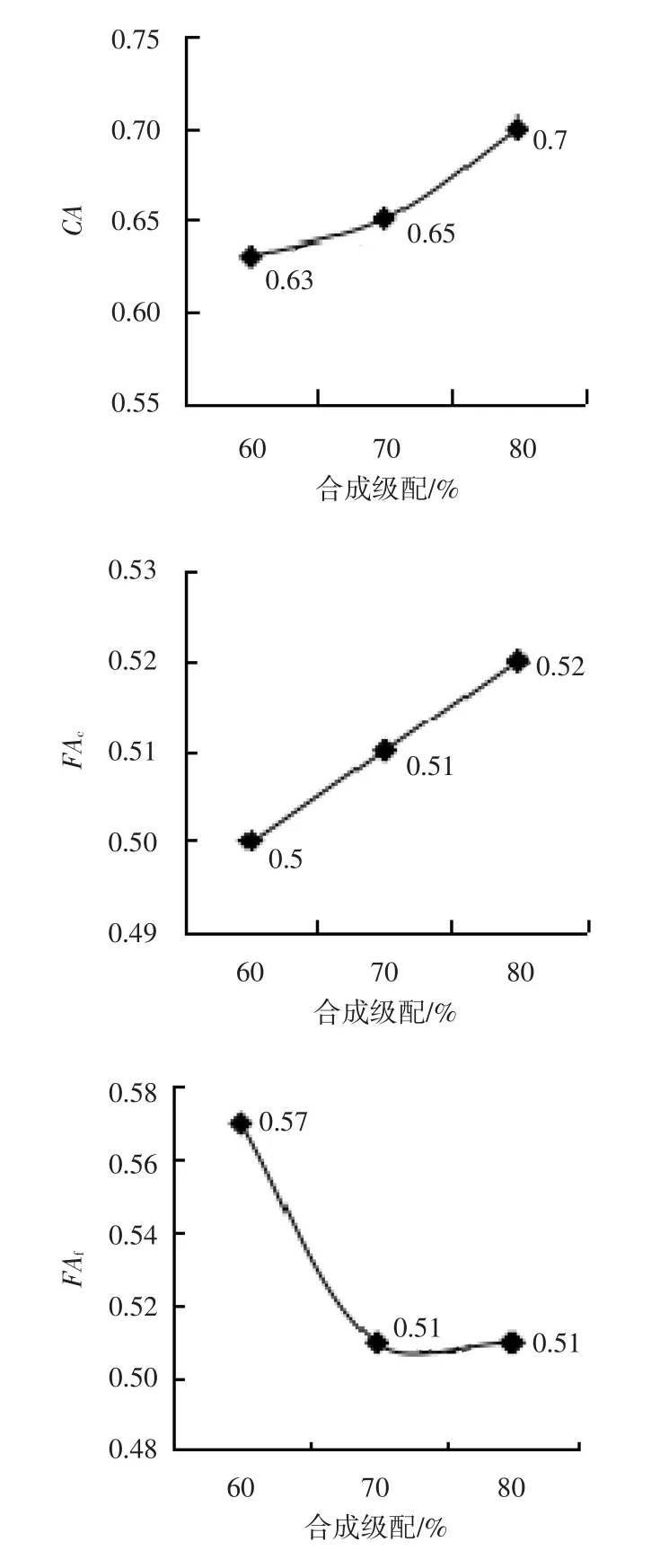
图7 合成级配掺量与修正检验参数关系

2.2.3 K值参数检验

上述贝雷法中CA反映的PCS以上筛孔粗集料的比例关系，而FAc、FAf反映的是PCS以下筛孔细集料之间的比例关系，若只采用三参数进行检验是无法反映出整个级配粗细集料比例的情况。以下例A、B级配为例进行说明见表7。

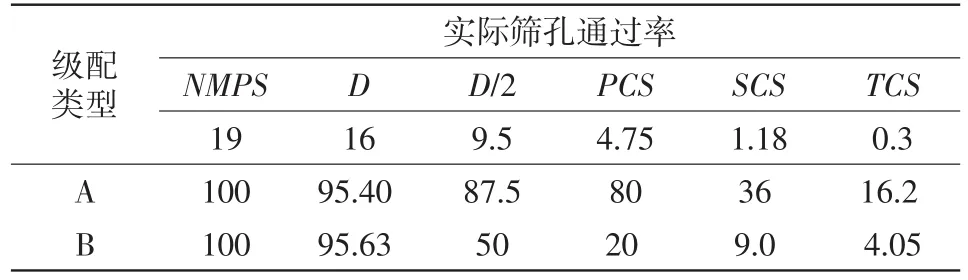
表7 A和B级配贝雷法检验示例%

表7中A和B级配CA比均为0.6、FAc比均为0.45、FAf均为0.45，其CA比、FAc比和FAf比均满足当前认为优良级配的合理范围内。但以PCS划分粗细集料，A级配粗细集料比值为2：8；B级配粗细集料比值为8：2，显然A、B级配均属于不良级配，其级配整体粗细集料比例严重失调。

贝雷法是利用设计密度（设计密度=粗集料松装密度×K，K的合理取值范围为95%～105%）［9］来控制粗细集料比例进行级配设计的，因此，在贝雷法检验三参数基础上增加一个检验参数，提出对已定级配反算松装密度的百分数K值，来分析整个级配粗细集料均匀性和级配骨架结构嵌挤情况。其公式：

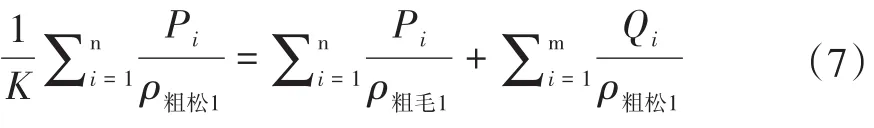
式中，K为松装密度的百分数修正值；Pi为i档粗集料用量；Qi为i档细集料用量；ρ粗松i为i档粗集料松装密度，g/cm3；ρ粗毛i为i档粗集料毛体积密度，g/cm3；ρ细捣i为i档细集料（0.075mm筛孔以下为填料）干捣密度，g/cm3。

将合成级配的粗集料各档集料分别按比例进行回配看成一档粗集料，其细集料各档料按比例进行回配看成一档细集料，上述公式简化处理见式（8）。用密度桶分别测定ρ粗松和ρ细捣，用挂篮法测定ρ粗毛。测定结果见表8和表9。

表8 ρ粗松和ρ粗毛测定结果 g/cm-3

表9 ρ细捣测定结果g/cm-3

结合表4将上述结果代入式（8）可反算K值，其结果见表10。

表10 反算K值结果 %

一般要求K值满足95%～105%区间时，其级配具有良好的压实性和骨架嵌挤结构，当K值高于105%时，粗集料颗粒嵌挤不密实使空隙率变大造成混合料难以压实；当K值低于95%时，细集料颗粒过量级配骨架结构不稳。由计算结果可知，3种掺量的合成级配满足95%～105%区间，其合成级配粗细集料有良好的均匀性和骨架嵌挤结构。

3 结语

利用CVi和Wi对旧集料进行分析，综合考虑级配离散性和权重，明确了旧集料在服役期间变异性贡献主要筛孔为16、13.2、2.36mm和0.075mm，采用细度模数进行级配设计，可改善级配变异性，用贝雷法对级配进行检验，用P理论筛孔对贝雷法检验参数进行修正，最后利用K值对合成级配进行检验分析，得出了合成级配粗细集料有良好均匀性和骨架嵌挤结构的结论。