建筑能耗异常数据的识别算法设计与仿真

赵 山，苏一帆

(华北水利水电大学土木与交通学院，河南 郑州 450045)

1 引言

建筑能耗在通常情况下是指建筑从建设前的材料、施工、到投入使用的整个过程中产生的能耗，这些能耗的计算是每个建筑企业管理过程中不可或缺的内容[1]。能耗计算是建筑的一种高级能耗分析形式，可针对建筑中的全部用能项目类别数据进行统计和计算，其可用于建筑成本的分析，掌握建筑各个项目类别的能耗情况，对建筑成本掌控具有重要意义[2]。但是在对这些数据计算时，会存在缺失或者受损，以及无效等异常数据，这些异常数据对于计算的结果存在较大影响。当数据中含有的数据类别较多时，识别的结果越容易受到影响。因此，在对各类能耗计算时，需准确识别能耗数据中的异常数据，保证计算结果的准确性。回归分析是一种用于数据分析的方法，其可通过相关的数据统计结果，针对数据间存在的某些关联构建回归分析方程，用于完成数据分析。回归分析存在两种方式，分别为线性以及非线性分析，回归分析使用过程中需要以数据为依据，构建回归方程后求解回归系数，采用相关性对其进行检验，获取相关系数，将其与实际情况相结合，确定目标的实际情况，实现需求的分析[3]。

当下用于识别建筑能耗异常数据的方法较多，例如文献[4]提出的基于分层聚合的异常数据识别算法和文献[5]提出的基于DCNDA算法的异常数据识别算法，均可完成单属性数据集中的异常数据识别，但是在多属性数据集中的异常数据识别的效果相对不够理想，异常数据数量越多，其识别效果越差，识别的相关系数较低。基于此，本文提出基于回归分析的建筑能耗异常数据识别算法，以回归分析理论为依据，构建回归模型，实现建筑能耗异常数据的识别，保证异常数据可被准确识别。

2 基于回归分析的建筑能耗异常数据识别

2.1 建筑能耗异常数据挖掘

2.1.1 数据挖掘

数据挖掘是识别的基础，为完成异常数据识别，需对建筑能耗数据进行挖掘[6]，本文采用梯度提升回归树完成建筑能耗数据挖掘，将建筑能耗数据定义为目标数据。该算法挖掘目标数据过程中，以挖掘目标数据的关联主特征为目标，则输出为

(1)

式中：f表示特征；k和k-1分别表示第k个和第k-1个数据。

为获取目标数据的密度特征，通过回归树分析方法完成，该特征属于统计分布概率，其计算公式为

(2)

式中：一个更新周期的差距存在tn+1和tn两个时刻；D表示量化特征分布集，属于本文算法进行挖掘的目标数据，求解互为信息量，且属于目标数据，采用梯度提升回归树完成[7]，其计算公式为

(3)

(4)

梯度提升回归模型的建立依据多队列调度方法完成，si={xj：d(xj，yi)≤d(xj，yl)}表示训练集，其中，d表示交互性统计数据，其属于目标数据；以其为依据获取目标数据的挖掘帧序列[8]

MinWH=min{w(cc)，h(cc)}

(5)

(6)

核函数依据式(5)和(6)的结果构建，对加权进行调整后可得出目标数据的统计输出和几何邻域[9]，分别为Nj*和NEj*(t)，同时获取目标数据挖掘的模糊聚类中心，其为

U={μik|i=1，2，…，c，k=1，2，…，n}

(7)

为获取回归树目标数据的分析目标函数，以关联规则为参考，其公式为

(8)

优化后聚类中心为

(9)

(10)

式中：适应度函数用m表示；xk表示目标数据样本；Vi表示关联数据样本；dik表示两者间的测度距离。空间聚类分布通过挖掘结果获取，其为

(11)

式(11)需满足(12)的条件：

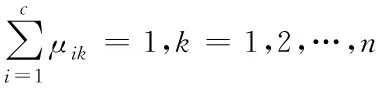
(12)

2.1.2 数据融合聚类

如果x(t)表示目标数据挖掘区域的离散序列，t=0，1，…，n-1；梯度提升基函数则用式(13)表示，且其属于设置的每一个队列范围内

u=[u1，u2，…，uN]∈RmN

(13)

目标数据挖掘最大梯度差的获取，需对目标数据的丢包率和传送延时进行分析后计算得出[10]，其公式为

(14)

关联指向性特征通过式(15)获取，且属于目标数据回归树，其为

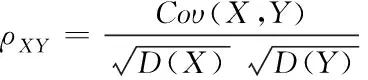
(15)

目标数据梯度差异化信息特征的提取在差异程度明显的情况下完成，且该差异属于梯度特征；为获取挖掘目标数据的输出，对挖掘到的数据进行融合[11]，得出输出结果

(16)

式中：差异化的队列融合属性数据分别用X、Y表示；密度函数分别用P(X)、P(Y)表示；概率分布用P(X∩Y)表示。

2.2 基于自回归模型的异常数据识别

2.2.1 自回归模型

基于回归分析理论构建自回归模型，其可根据变量自身存在的规律完成。为准确识别目标数据中的异常数据，本文将残差平方和(SSE)引入模型中，完成新的统计量建立，用于识别数据中的异常数据[12]。回归模型公式为

yi=β0+β1xi1+β2xi2+…+βpxip+εi，i=1，2，…，n

(17)

式中：回归系数用βj(j=0，1，…，p)表示；随机误差和阶数分别用εi和p表示。

异常数据识别变量用γi表示，将其引入各个识别数据中，引入γi后模型成为均值转移模型，其为

yi=β0+β1xi1+β2xi2+…+βpxip+δiγi+εi，

i=1，2，…，n

(18)

根据式(18)可知数据是否为异常值，可通过γi判断。

模型在进行异常数据识别时，无法确定是否存在异常数据，因此，如果异常数据不存在模型中，则模型可通过式(19)表示

Y=Xβ+ε

(19)

SSE=YT(I-H(X))Y

(20)

2.2.2 异常数据的计算和识别

将获取的差异化属性数据特征分别输入至模型中，通过模型进行异常数据的计算和识别。

如果输入模型中的数据为异常数据，则表示γk=1，δk则表示该异常数据的大小；除此之外的数据均为非异常数据，则此刻SSE的计算公式为

SSEk=(Y-δkIk)T(I-H(X))(Y-δkIk)

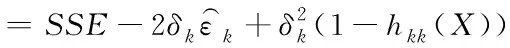
(21)

(22)

将式(22)的结果带入式(21)中进行求解后得出SSEk=SSE-Δk，其中

(23)

式中：在数据为异常数据的情况下，Δk表示残差平方和。

3 测试分析

选取某建筑企业2019年多属性建筑能耗统计数据集为测试对象，数据集数量共1550个，该数据数量中包含两种异常数据，分别为缺失数据和无效数据。数据集中包含三种属性数据，分别为建筑材料数据数量650个(异常数据24个)、施工数据550个(异常数据17个)、投入使用数据350个(异常数据5个)。采用Matlab软件完成，回归树迭代次数为200次。

数据特征分布集的挖掘是异常数据识别的基础。采用本文算法挖掘数据集，获取数据特征分布集，结果见图1。

图1 数据特征分布集

根据图1测试结果可知：获取的数据特征分布集中，分散三种数据的特征，说明本文算法具备数据特征挖掘性能，可获取数据集中不同属性的数据特征分布集，为异常数据识别提供依据。

为分析本文算法的特征挖掘效果，采用文本算法对图1获取的数据特征分布集进行挖掘，获取不同属性数据特征，用于分析本文算法数据挖掘效果，结果见图2。

图2 空间聚类分布结果

根据图2测试结果可知：本文算法可根据不同特征的聚类中心，有效完成不同属性数据特征聚类，并且实现不同属性特征的分类聚类。该结果表明：本文算法的聚类效果良好，可有效依据不同数据特征属性，可靠完成数据的特征分类聚类。

为测试本文算法对于异常数据的识别效果，进行异常数据识别，在单属性施工数据特征中第35个识别数据上引入大小为-22的缺失数据，测试本文算法对其识别效果，见图3；在单属性建筑材料数据特征中第125个和155个识别数据上，分别引入大小为19和-16的无效数据和缺失数据，测试本文算法对其识别效果，见图4；在多属性数据中，第445个识别数据上，同时引入大小为31和-34的无效数据和缺失数据、第1265个识别数据上，同时引入大小为38和-44的无效数据和缺失数据，测试本文算法的识别效果，见图5。

图3 单一属性数据中的一种异常数据识别结果

图4 单一属性数据中的多种异常数据识别结果

图5 多属性数据中的多种异常数据识别结果

根据图3、图4和图5测试结果可知：单一类型数据中只存在一种异常数据时，本文算法可较好完成异常数据的识别；当存在的异常数据为多种时，依旧可准确识别出引入的所有数据；在综合类数据中，当两种异常数据同时出现在一个识别数据上时，本文算法仍能够可靠完成异常数据的识别；同时，在识别引入的异常数据的同时，数据集中原有的异常数据均可有效识别出。该结果表明：本文算法可同时完成单一数据中已有的和引入的异常数据识别；综合数据中的已有的和引入的并发多种异常数据识别，并且识别效果良好，在不同类别的异常数据同时存在一个数据上时，依据可准确识别。

为进一步衡量本文算法对于异常数据的识别性能，将文献[4]的基于分层聚合的异常数据识别算法和文献[5]的基于DCNDA算法的异常数据识别算法作为本文算法的对比算法，以相关系数作为衡量标准，采用三种算法对数据中的异常数据进行识别，计算三种算法识别的相关系数，以此分析三种算法的异常数据识别性能，结果见图6。相关系数值越高，表示算法的识别性能越好。

相关系数计算公式为：

(24)

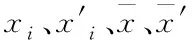
图6 三种算法的相关系数测试结果

根据图6测试结果可知：对多属性数据集的异常数据进行识别时，本文算法识别相关系数值最佳，并且异常数据量的增加，相关系数值的变化较小，没有受到数量增加的影响，呈现缓慢小幅度的增长趋势；两种对比算法异常数据识别的相关系数值明显低于本文算法，并且异常数据数量的增加，两种算法相关系数呈显著下降趋势，说明在多属性数据集中的异常数据数量越多，两种算法的识别效果降低。该测试结果表明：本文算法的异常数据识别性能良好，多属性数据集中异常数据识别的相关系数均在0.972以上，显著优于两种对比算法。

4 结论

建筑能耗数据对于建筑企业的成本预算和利润计算存在直接关联，因此，各建筑企业需依据建筑能耗数据完成能耗计算。由于数据中会存在各种异常数据，对于计算结果存在直接影响，本文提出基于回归分析的建筑能耗异常数据识别算法，识别建筑能耗数据中的异常数据。经测试：该算法具备较好的数据分类聚类效果，可根据数据属性的差异完成数据特征挖掘，并且有效完成多属性数据中异常数据的识别，识别性能优于两种对比方法，可用于建筑能耗异常数据的识别，保证识别结果具备良好的可靠性，为建筑企业的成本预算以及利润核算提供可靠依据。