起波钢筋高速动态拉伸力学性能研究*

刘思嘉，陈 力，曹铭津，周东雷，樊 源，陈 欣

（1. 东南大学爆炸安全防护教育部工程研究中心，江苏 南京 211189；2. 解放军93204 部队，北京 100068）

起波钢筋是通过冷加工方式将普通受拉纵筋局部弯折后形成波形凸起的钢筋，最初是为了改善钢筋混凝土（reinforced concrete，RC）结构在地震荷载作用下的塑性铰形成机制。最早先由冯鹏等提出，并将其应用在RC 梁底部反弯点处，目的是使RC 梁构件能在地震作用下先于柱构件破坏，实现了“强柱弱梁”以及塑性铰的转移。杨建翔等则进一步对采用起波配筋RC 梁柱子结构的抗连续性倒塌性能进行了研究。

起波钢筋除了具有转移RC 构件塑性铰的能力之外，其在受荷拉直的过程中具有极强的变形性能，如图1 所示。因此，陈力等提出了在RC 梁底配置起波钢筋来提高RC 梁抗爆性能，并基于能量法推导得到了起波配筋混凝土梁（reinforced concrete beam with kinked rebar，KRC）在爆炸荷载作用下的抗力动力系数无量纲计算公式。陈力等进一步的落锤冲击气囊加载试验工作也充分证明：起波配筋能够增加梁塑性铰数量和提高梁体变形吸能能力，并显著提高RC梁的抗冲击性能。

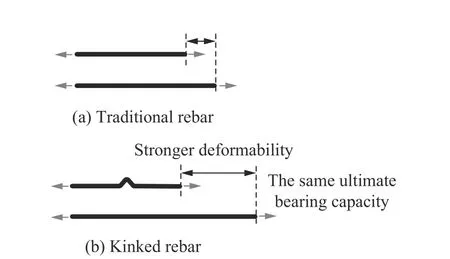
图1 传统钢筋与起波钢筋示意图Fig. 1 Kinked rebar compared with traditional rebar

爆炸荷载是一种峰值高、历时短的强动载，爆炸荷载作用下的构件会发生快速变形。钢材、混凝土等材料均具有应变率效应，其强度、弹性模量等力学性能指标均随应变率提高而增大。然而，起波钢筋在爆炸荷载作用下的快速拉伸变形效应显然与普通平直钢筋有显著不同，KRC 梁现有的抗爆研究成果均由拟静力试验、低速落锤冲击试验和理论推导得出，对起波钢筋的快速拉伸效应缺少研究。

为进一步研究KRC 梁在爆炸荷载作用下的动力响应，建立抗爆设计方法，对起波钢筋的快速变形性能进行研究十分必要。研究发现，起波纵筋在被拉直的过程中，其弯折角度会发生巨大变化，弯折点的内外表面应变和应变率差别较大，且其拉伸变形机制与弯折点的转动弯矩有较大关联，尽管已有大量文献给出了平直钢筋的应变率效应计算公式，但是仅以平直钢筋应变率效应公式来计算起波钢筋的快速变形效应误差很大。

本文中将针对起波钢筋高速动态拉伸力学性能开展实验和理论研究，提出起波钢筋等效应变率的概念，揭示起波钢筋的拉伸变形作用机制，建立起波钢筋等效应变率与平直钢筋应变率之间的关系，并进一步讨论各种因素对起波钢筋快速变形性能的影响规律。基于等效应变率建立的起波钢筋弹性极限强度动力放大系数（dynamic increase factors，DIF）模型，可为工程应用提供理论依据。

1 抗拉变形作用机制

由于起波钢筋经过了局部预先弯折，其在拉直过程中的变形机制与普通平直钢筋有很大不同。如图2 所示，起波钢筋在受力拉直过程中，钢筋两端沿轴心方向向外移动，钢筋的弯折截面位置将产生弯矩。

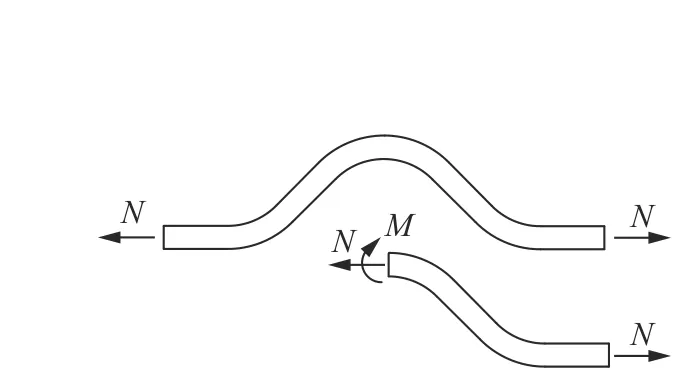
图2 弯折位置受力示意图Fig. 2 Forces at the bending position

为了降低成本，钢筋起波通常采用冷加工，钢筋弯折段会产生塑性损伤。在拉伸变形过程中，由钢筋内力产生的弯矩将会使弯折位置发生变形旋转，而钢筋的平直段弯矩很小。若将起波钢筋整体视为一种单一材料，可以根据单轴拉伸试验得到起波钢筋的等效应力-等效伸长率曲线（参见文献[1]中的图，图中的等效应力为试验机拉力与钢筋面积的比值，等效伸长率为钢筋伸长量与拉伸计两测点之间长度的比值），则该曲线可以描述为“弹性段-平台段-强化段-屈服段”四折线模型，如图3 所示。因此当拉伸力较小时，弯折位置弯矩较小，仅发生弹性变形，起波钢筋整体处于弹性工作阶段。随着拉力不断增大，弯折截面弯矩增大，根据经典塑性力学理论，待弯折截面全部纤维进入塑性后，弯折位置开始发生塑性变形，起波钢筋等效应力-等效伸长率曲线则由弹性段进入平台段。由此，本文中提出了起波钢筋静态弹性极限强度计算方法，具体内容见附录。

图3 起波钢筋四折线模型Fig. 3 Four-line model of kinked rebar

起波钢筋其实是一种微结构，其拉伸变形机制与平直钢筋不同，其拉伸力学性能受到起波形状和钢筋直径的共同影响，很难用现有的平直钢筋材料应变率效应公式来计算表征起波钢筋的快速变形性能。起波钢筋在受荷拉直过程中产生的快速变形效应主要由弯折截面材料的应变率效应产生，由此本文中提出了起波钢筋等效应变率的概念，即将起波钢筋整体视为一种等效材料，将钢筋起波弯折位置截面的平均应变速率定义为起波钢筋等效应变率。

2 等效应变率计算方法

起波钢筋端部沿轴向向外运动后，起波形状变化示意图如图4 所示。如前所述，起波钢筋在拉伸过程中，弯折位置发生变形旋转，而钢筋的其余平直段基本不发生弯曲变形，因此可以假设起波钢筋在拉直过程中，其起波斜边长度不变，钢筋端部每沿轴向拉伸运动d，其起波顶点沿轴运动d，起波顶角α 也相应增大dα，则d可表示为：

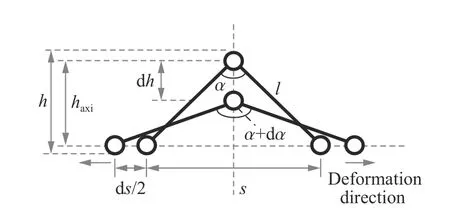
图4 起波形状变化示意图Fig. 4 Diagram of the shape change of kink

由于起波矢高=+，且钢筋直径为常数，因此d=d。

3 冲击拉伸试验

3.1 试件设计

起波钢筋的冲击拉伸试验选取防护工程中常用的直径为18 mm 的HRB400 钢筋，试件如图5 所示。共设计了3 组（共计36 根）钢筋试件，各组起波矢高分别为40、50、60 mm，每组12 根试件，其中每3 根对应4 种不同的拉伸速度，分别为2.5、5、10、15 m/s，其主要参数见表1。

表1 试验工况Table 1 Test parameters

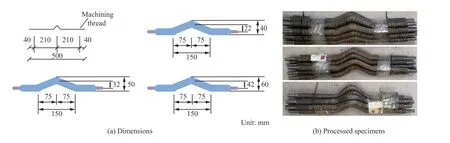
图5 起波钢筋试件Fig. 5 Specimens of the kinked rebars

考虑到冲击拉伸试验机最大拉力为100 kN 的限制，为保护试验机，需对钢筋两端进一步加工，减小钢筋截面面积。本次试验对钢筋的两端进行切削和打磨，制成直径10 mm 的细螺纹钢。由钢筋屈服强度为400 MPa、极限强度为590 MPa，计算得到屈服拉力为31.4 kN、极限抗拉力为46.315 kN，符合拉伸试验机的使用要求。

考虑到起波矢高的影响，参考附录中确定弹性极限强度的方法，代入图5 中的试件设计参数，计算得到起波钢筋的静态弹性极限强度σ 与抗拉力，见表2。结果表明，起波钢筋的弹性极限抗拉能力均小于螺纹处10 mm 直筋的极限抗拉力，考虑到钢筋的应变率效应，在动态拉伸条件下，此试件设计方案能够测得起波钢筋弹性极限拉力。

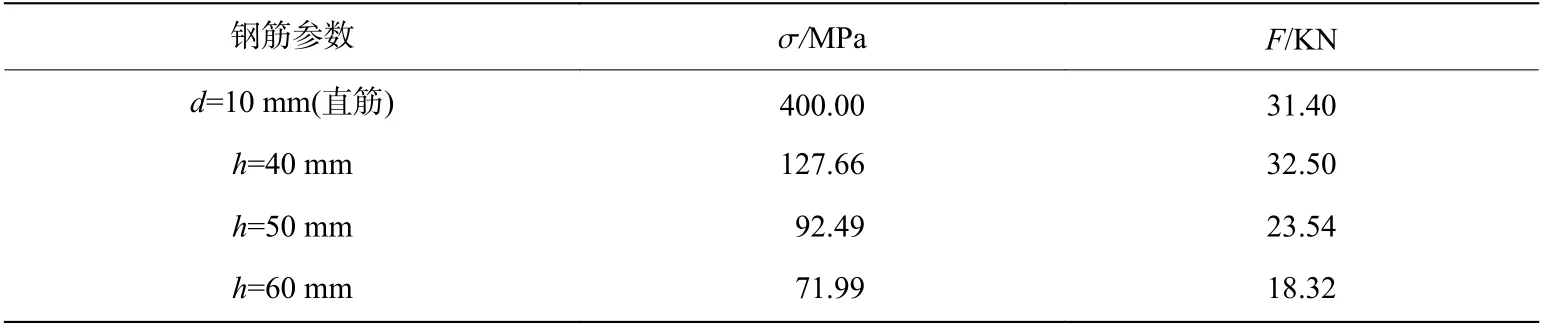
表2 起波钢筋的静态弹性极限强度和抗拉极限Table 2 Elastic ultimate strength and tensile capacity of the kinked rebar under static loading

3.2 加载系统

使用的INSTRON 高速动力冲击加载系统对起波钢筋进行高速拉伸试验。该加载系统采用先进的液压控制技术，可对试件以恒定速度进行冲击拉伸或压缩，加载速度0.1～20 m/s、荷载量程0～100 kN。图6(a)为试验装置整体布置，图6(b)为试验加载方案。

图6 试验加载系统Fig. 6 Loading system

使用加速等待装置确保作动器达到稳定的预期速度，加速等待装置由纯钢套筒和实心杆组成（见图7），实心杆允许在套筒中自由滑行一段距离。试件安装时，分别将套筒与作动器连接，钢筋通过螺栓与实心杆连接。在钢筋拉伸初期，套筒随作动器先于实心杆加速至预期速度，当实心杆达到滑行距离极限（套筒底部）后，套筒牵拉实心杆和钢筋按预期拉伸速度进行加载。此方法可以有效保证钢筋的拉伸速度稳定。

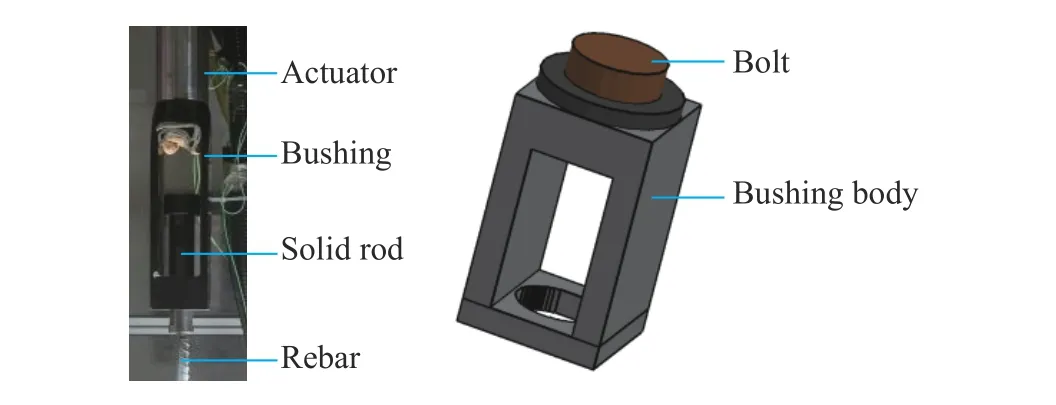
图7 加速等待装置Fig. 7 Accelerated holding device

4 试验数据分析

4.1 弹性极限强度

图8 为各组起波钢筋在各拉伸速度下的等效应力-等效伸长率散点图，其中等效应力由试验机测得的拉力除以钢筋截面面积得到，等效伸长率由伸长量除以钢筋原始标距得到。

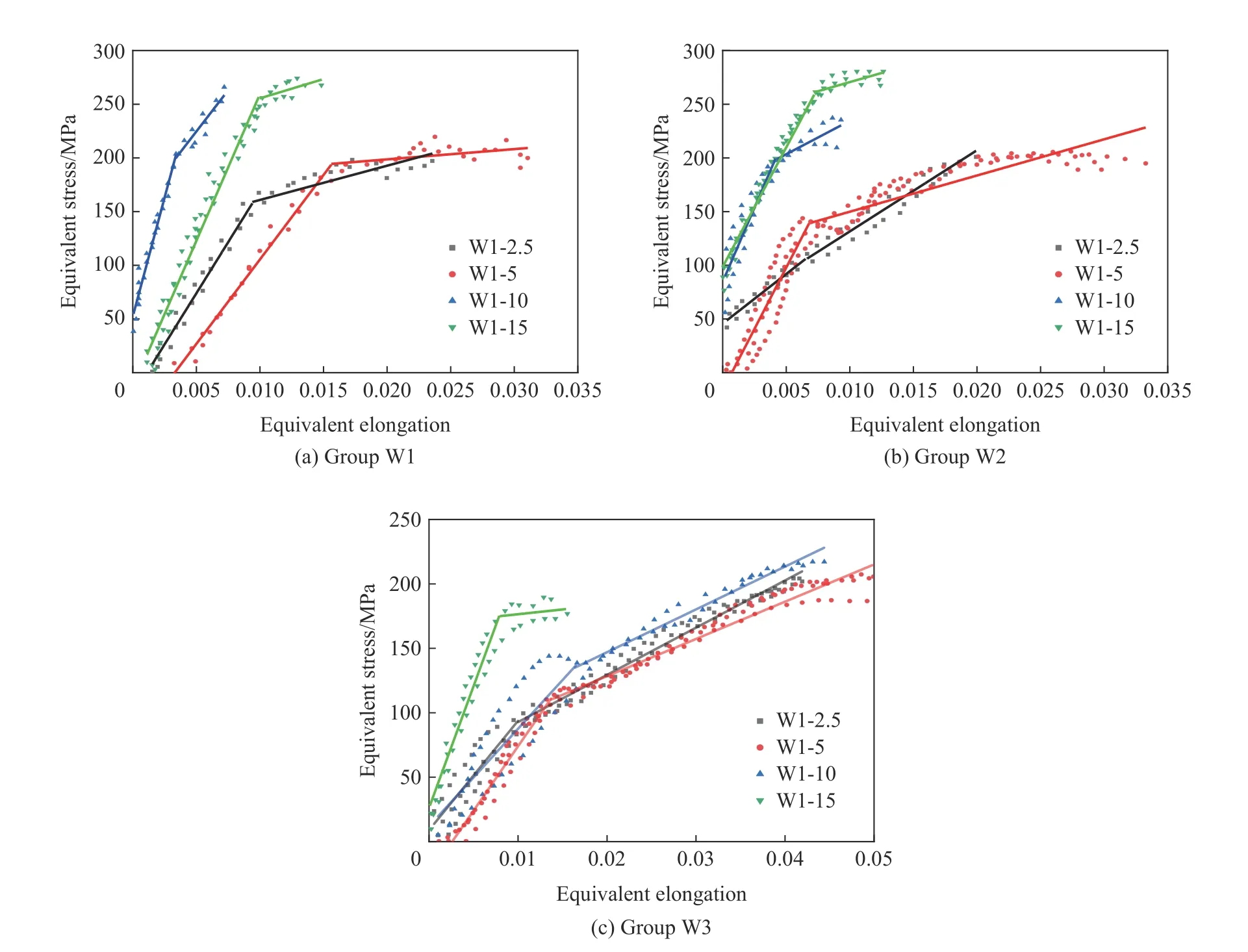
图8 各组起波钢筋等效应力-等效伸长率曲线Fig. 8 Equivalent stress-equivalent elongation curves of each group

如前所述，静态拉伸情况下起波钢筋的等效应力-等效伸长率曲线可描述成“弹性段-平台段-强化段-屈服段”四折线模型。而在动态拉伸条件下，根据观察到的各组散点数据，可以初步判断高速拉伸时也可以用类似的模型来描述：等效应力较小时，钢筋弯折位置截面发生弹性应变，且弹性段强度较低；待弯折位置截面产生塑性应变后，起波钢筋开始发生大变形，以较小的强度进入平台拉直段。相对于文献中的四阶段模型，本试验的拉直段平台现象并不明显，且具有强化的趋势，这主要是由于相对于静载试验，冲击拉伸试验所用钢筋直径较大所致。由于试验机最大拉力的限制，各组起波钢筋拉伸过程只能最多量测到平台拉直段，并不能量测试件拉直后（强化段-屈服段）甚至拉断的整个过程。

对各组散点图中处于两个不同阶段的散点数据进行线性拟合，两段不同斜率直线的连接点对应的等效应力值即为起波钢筋弹性极限强度。而弹性极限强度作为曲线的第1 个特征点，此后应力沿“平台-强化-屈服段”折线呈上升趋势。若能定量地确定各因素对弹性极限强度的影响，则可揭示各因素对起波钢筋整个动态抗拉性能的影响规律。表3 为提取出的各组起波钢筋弹性极限强度，以下讨论各因素对弹性极限强度的影响。

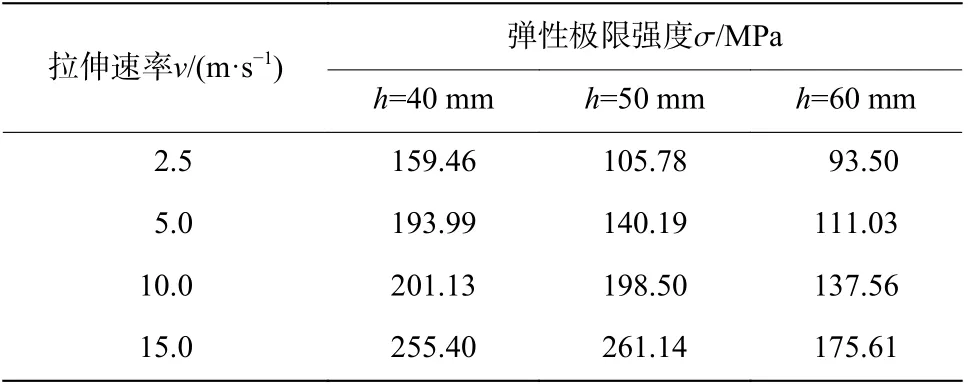
表3 各组起波钢筋的弹性极限强度Table 3 Elastic ultimate strengths of the kinked rebars

4.2 拉伸速度

由表3 中数据可知，在起波矢高相同的情况下，起波钢筋弹性极限强度明显随拉伸速度的增大而增大。当起波矢高=40 mm 时，随着拉伸速度的增大，弹性极限强度由127.66 MPa 增大至255.40 MPa，增大了1 倍；当起波矢高=50 mm 时，随着拉伸速度的增大，弹性极限强度由92.49 MPa 增大至261.14 MPa，增大了1.82 倍；当起波矢高=60 mm 时，随着拉伸速度的增大，弹性极限强度由71.99 MPa 增大至175.61 MPa，增大了1.44 倍。可以发现，起波钢筋在快速变形的情况下存在明显的应变率效应。

4.3 起波矢高

由式（8）可知，在相同的拉伸速度下，起波矢高不同时，起波钢筋的等效应变率也不同，因此，起波钢筋弹性极限强度同时也受到起波矢高的影响。

若将起波钢筋结构整体视为一种材料，则可通过起波钢筋弹性极限强度DIF（动态拉伸条件下起波钢筋的弹性极限强度与静态拉伸下弹性极限强度的比值）来定量描述其动态拉伸力学性能。然而，其快速拉伸变形的力学效应受到起波矢高、钢筋直径和拉伸速度的共同影响，单独以起波钢筋的等效工程应变率来描述其应变率增强效应是不全面的，而以等效应变率作为评价标准则可以避免等效工程应变率的不足。考虑到当拉伸加载时为静态，DIF 必为1，同时参考Johnson-Cook 材料本构模型中考虑应变率效应的因式 ( 1+ln ε˙) 的自然对数形式，可假设弹性极限强度DIF 随等效应变率的变化规律为：

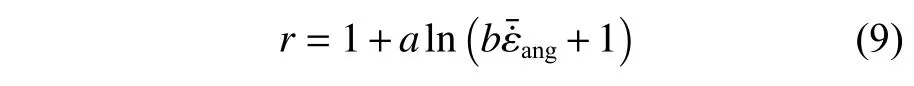
由图9 中的曲线可以看出，在等效应变率为0～99.76 s的范围内，弹性极限强度DIF 随着起波矢高的增大而增大；但当等效应变率增大至一定值后（99.76 s），起波矢高为50 mm 时DIF 最大。分析可以发现，弹性极限强度DIF 受起波矢高的影响有两方面的趋势：一方面为静态弹性极限强度，根据附录中确定静态极限强度的方法，当动态弹性极限强度σ相同时，随着起波矢高的增大，静态弹性极限强度减小，DIF 相应增大，DIF 与起波矢高呈正相关；另一方面为等效应变率，根据式(8)，相同拉伸速度下，随着起波矢高的增大，等效应变率减小，对于同种材料而言，DIF 相应减小，DIF 与起波矢高呈负相关。

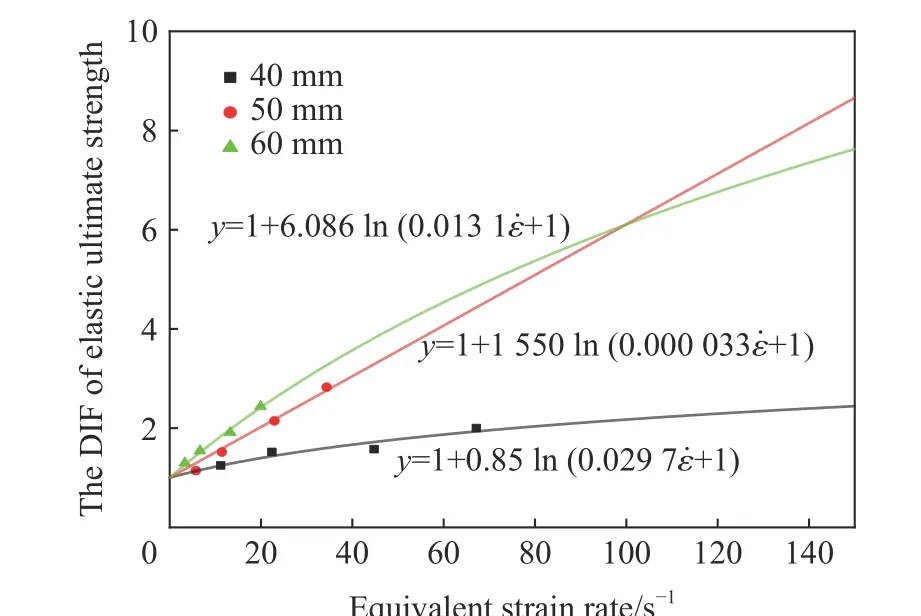
图9 起波钢筋弹性极限强度DIF-等效应变率曲线Fig. 9 DIF-equivalent strain rate curves of the kinked rebars

弹性极限强度DIF 受以上两种因素（一种正相关因素，一种负相关因素）的共同影响，当等效应变率较小时，正相关因素起主要作用，此时DIF 随起波矢高的增大而增大。待等效应变率达到一定值后，负相关因素起主要作用，起波矢高60 mm 的DIF 反而小于起波矢高50 mm 的DIF。由此存在一个最优起波设计矢高，使得在高应变率下（本次试验大于99.76 s）起波钢筋弹性极限强度DIF 达到最大。

4.4 弹性极限强度DIF 计算模型

由上述分析可知，在构建起波钢筋弹性极限强度DIF 计算模型时，需考虑DIF 受到等效应变率和静态弹性极限强度两种因素的共同影响。根据附录和式(8)可知，这两种因素又与起波矢高相关，因此可将DIF 计算模型中的变量、与起波矢高建立拟合关系，从而体现DIF 受到等效应变率和静态弹性极限强度两种因素的共同影响。提取出的、值如表4 所示，拟合结果如下：

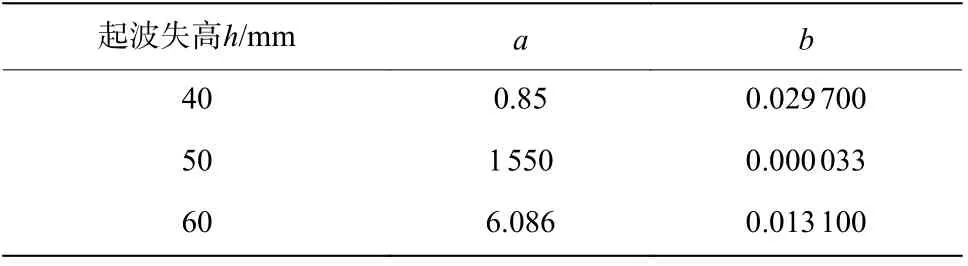
表4 三组DIF 拟合公式中的 a 、 b 值Table 4 Values of a and b of the three groups of the kinked rebars

综上所述，若已知起波矢高和等效工程应变率的具体数值，由式(12)可得到起波钢筋弹性极限强度的DIF 值，弹性段极限强度即可确定。

5 结 论

通过理论分析与动态拉伸试验相结合的方法，研究了起波钢筋的高速拉伸动力性能，揭示了起波钢筋快速拉伸变形机理，确定了起波钢筋静态弹性极限强度计算方法，并由此建立了起波钢筋弹性极限强度DIF 计算模型，可为进一步推动起波配筋技术在防护工程上的应用提供理论依据。主要结论有：

（1） 高速拉伸条件下，起波钢筋的动态变形机制与静态拉伸情况相似，弯折截面的屈服状态决定了起波钢筋的弹性极限拉伸强度；

（2） 起波钢筋快速变形情况下的力学性能存在应变率效应，其弹性极限强度随拉伸速度的增大而显著提高，本文中提出的等效应变率可以较好地描述起波钢筋的应变率效应；

（3） 起波矢高对起波钢筋弹性抗拉极限强度DIF 有增大和减小的双重影响，在高应变率情况下存在一最优起波矢高，使得起波钢筋弹性抗拉极限强度DIF 最大。

从附录中确定起波钢筋静态弹性极限强度计算方法可知，起波钢筋静态弹性极限强度除了与起波矢高有关，与起波间距之间也有一定的关系。本文中仅讨论了起波矢高对起波钢筋弹性极限强度DIF 的影响，下一步工作将通过试验研究进一步考虑起波间距的影响。

图10 中给出了起波钢筋从开始受力到弯折位置开始发生塑性变形的整个过程。起波钢筋为对称结构，取一半进行受力分析，由于在弯折位置发生塑性变形之前整个钢筋形状并不发生改变，因此起波顶角截面处边界按固支边界处理，如图10(a)所示。起波钢筋端部在受到轴力之后，起波处的各个截面都受到弯矩与轴力的共同作用。各个截面受到的轴力相同但起波顶角处截面所受的弯矩最大，因此在整个弯折位置发生塑性变形之前，起波顶角处截面首先成为第1 个塑性铰，进入全截面屈服，如图10(b)所示。

图10 起波钢筋发生塑性变形过程Fig. 10 The plastic deformation process

由图解法，如图11 所示，绿色曲线为式(17)代表的轴力与弯矩共同作用的极限状态方程，黑色曲线为式(18)代表的加载方程，两条曲线交点的、值即为起波顶角处截面成为第1 个塑性铰时的弯矩与轴力值。但此时求得的名义应力并非起波钢筋的弹性极限强度。如图10(c)所示，在起波顶角处截面成为第1 个塑性铰之后，钢筋端部有向上翘曲的趋势，由于端部受拉伸仪器夹具限制，其弯折部分还不能发生转动变形，此时夹具将会对端部有一个向下的支持力，的出现将导致起波底角处截面成为第2 个塑性铰。只有在出现第2 个塑性铰后，弯折部分才能发生转动变形，即由第2 个塑性铰出现时刻所求得的名义应力为起波钢筋的弹性极限强度。

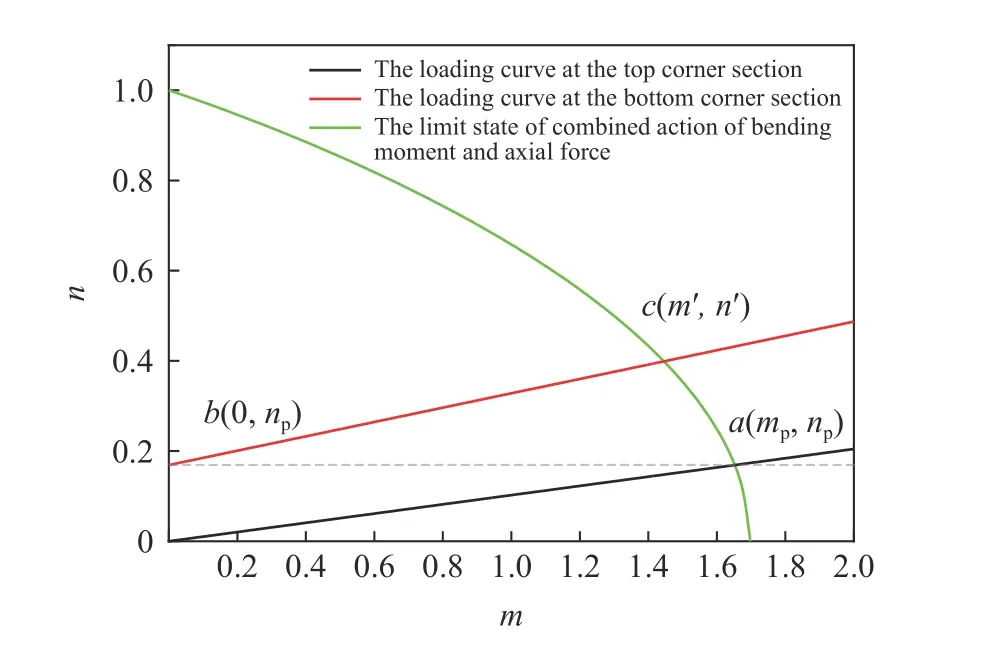
图11 第2 个塑性铰出现后起波钢筋的受力分析Fig. 11 Force analysis of the steel bar after the second plastic hinge appears

如图12 所示，取出从起波底角至端部长度的平直段钢筋进行受力分析，设出现支持力之后轴力为，起波底角处截面弯矩为，起波顶角处截面弯矩为，可得到以下关系式：

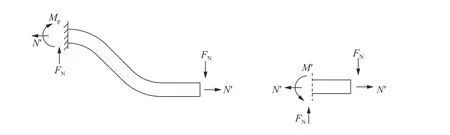
图12 端部支持力出现后起波钢筋受力分析Fig. 12 Force analysis after the occurrence of end support force

式中：为钢筋标距，为起波间距。

联立式(19)～(20)，消去以及归一化之后，得到下式：

再由图解法，如图12 所示，绿色曲线为式(17)代表的轴力与弯矩共同作用的极限状态方程，红色曲线为式(22)代表的底角处截面加载方程，由两条曲线求得交点为点(,)。在起波底角处截面由纯受轴力状态向受轴力、弯矩共同作用状态转变过程中（即图12 中由点移动至点），对于起波顶角处的截面，由于的出现，该处截面的轴力与弯矩的比例关系也发生改变，但顶角截面仍维持塑性极限状态，其在图12 中的代表点同时移动至点。

因此经上述分析，图12 中的点()即为起波钢筋静态弹性极限强度点，由求得的名义应力：

式中：σ为钢筋屈服强度。

式(23) 即为起波钢筋的静态弹性极限强度。由此方法计算得到文献[1]中各种起波钢筋试件的静态极限强度，并与文献中的数据进行比较，结果如表5 所示。因试件F10-60 弹性极限强度试验值与理论计算值的误差与其他试件相比出入很大，且该试验值并不满足弹性极限强度受起波间距的影响规律，将该数据剔除。

从表5 可知，理论值与试验值误差范围为9.6%～31.3%，原因在于式(22)中的σ是钢筋屈服强度。起波钢筋在预制过程中起波顶角处截面中性轴以上的纤维受到拉力作用，中性轴以下的纤维受到压力作用，并且都是加载到一定程度产生塑性变形之后卸载形成预制起波形状。之后，在受到轴力作用时，起波钢筋受荷拉直相当于反向加载的过程，此时起波顶角处截面中性轴以上的纤维受到压力作用，中性轴以下的纤维则受到拉力作用（同理，起波底角处截面也是反向加载）。在“加载-卸载-反向加载”的过程中，钢筋材料存在包辛格效应，即反向的屈服应力的绝对值比初始屈服应力小。

因此，考虑到钢筋材料的包辛格效应，需要对钢筋屈服强度进行一定的折减，本文中取σ=0.8σ。修正后的强度和误差见表5，从表5 可知，试件F10-45 误差最大，为37%，这是由于计算得到的理论值比试验值小，实际上，由于钢材的包辛格效应，计算得到的理论值应比试验值大，所以本数据的测试结果存疑，可以剔除。而修正后其余试件的静态屈服强度误差均在2.4%～14.1%之间。因此取0.8 的折减系数可以较好地考虑钢材包辛格效应的影响。修正后的起波钢筋静态弹性极限强度计算公式为：

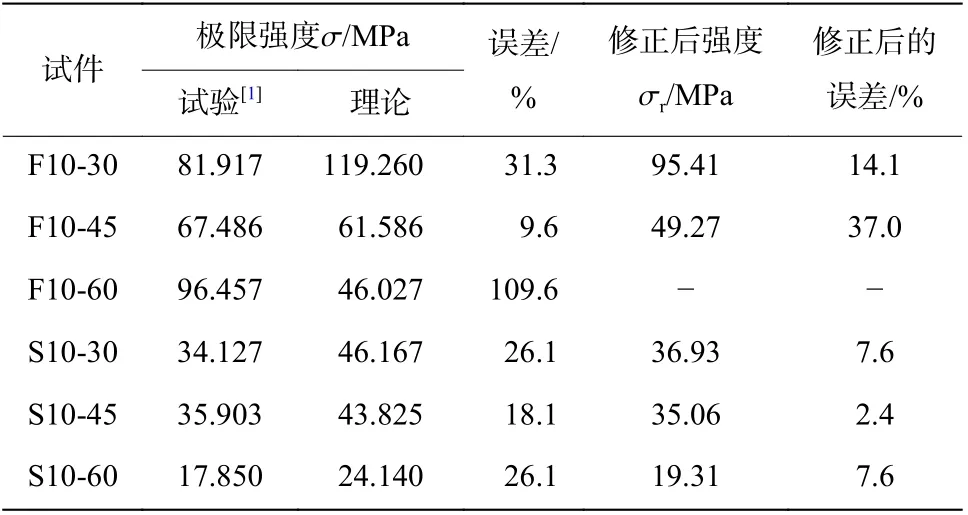
表5 起波钢筋静态弹性极限强度理论值与试验值对比Table 5 Comparison between the theoretical and experimental values of the static elastic ultimate strength