受轴向冲击薄壁圆管的几何畸变相似律研究*

杨磊峰，常新哲，徐 绯，王 帅，刘小川，惠旭龙，李肖成

（1. 西北工业大学航空学院计算力学与工程应用研究所，陕西 西安 710072；2. 中国飞机强度研究所结构冲击动力学航空科技重点实验室，陕西 西安 710065）

薄壁圆管凭借其自身结构简单，变形、破坏模式稳定，轴压峰值力与平均力的可设计性以及能量吸收可控等优点，被广泛地应用于抗冲击领域，如飞机坠撞防护、缓冲器以及其他的工程领域等。薄壁圆管在轴向冲击压缩载荷作用下的屈曲问题长期以来备受关注。Alexander 等针对理想刚塑性材料制成的薄壁圆管，应用具有塑性铰的简化轴对称变形模式，推导出了轴对称条件下的轴压载荷下薄壁圆管的平均力。该变形模型获得了学者的广泛认可并得到了大量的推广应用。Abramowicz 等基于Alexander等的研究结果，对薄壁圆管轴对称变形时的折皱长度公式进行了修正，试验结果表明，修正后的公式可以较好地预测轴对称变形以及金刚石变形模式下的薄壁圆管的折皱长度。Karagiozova 等对受轴向冲击的弹塑性材料薄壁圆管的峰值载荷进行了研究，分别获得了Mises 屈服条件和Tresca 屈服条件下的峰值载荷。Lu 等在Alexander 等的基础上，提出了一种新的运动位移场，求解了更加合理的薄壁圆管折皱长度公式，并改进了轴对称变形下的载荷位移曲线。这些重要的研究为理解轴向冲击圆管的变形行为奠定了理论基础。

结构的冲击承载安全性是结构设计的重要组成部分，但是大结构的全尺寸冲击试验极其耗时耗力，需要付出大量的人力物力和财力，因此一般使用比例模型试验来替代结构全尺寸原型。Jones通过量纲分析，建立了结构冲击问题的经典相似理论，由于该理论基于简单的几何相似关系，因而广受重视。Oshiro 等采用新的量纲分析体系克服经典相似律解决材料相似时的理论困难，提出一种通过修正冲击速度或密度的方式，来适应应变率敏感性以及比例模型与原型使用不同材料时的畸变问题的相似方案。王帅等通过建立应变率区间上比例模型预测的流动屈服应力与原型流动屈服应力的最佳逼近关系，获得了速度比例因子的直接相似关系，从而扩展了相似律的应用技术。李肖成等通过调整薄板结构的厚度，修正了比例模型与原型采用不同材料时引起的畸变问题。秦健等基于VSG 量纲体系，研究得到了加筋板结构在水下爆炸冲击波作用下模型和原型的动态响应相似关系。

然而，在实际工程应用中还存在加工制造等难题，通常，薄壁圆管的厚度不一定能够和半径以及长度按照相同的比例因子进行缩放，这就会产生畸变模型，从而导致原有的相似律失效。Alves 等提出单独考虑几何畸变以及应变率效应，并通过经验方法不断迭代几何畸变对缩比相似影响所占的比重来修正速度比例因子。Mazzariol 等通过塑性弯矩的无量纲数改进了经验法，提出了一种解决薄板和梁结构的几何畸变问题的新方法。Wang 等基于定向量纲的分析方法，从理论上克服了几何畸变的相似律难题，针对薄板冲击模型系统表达了几何畸变的相似体系。尽管这些研究在解决几何畸变相似律的问题上取得了重要的理论进步，但是针对薄壁圆管的几何畸变修正方法的研究分析并未开展，而且在实际的受轴向冲击载荷作用的薄壁圆管缩比相似分析中厚度畸变几乎不可避免。

本文中针对受轴向冲击载荷作用的薄壁圆管，基于方程分析与量纲分析，以载荷、位移和能量为关键设计参数，推导薄壁圆管几何畸变的动态响应相似律，此方法可推广至考虑材料应变率以及应变硬化效应和几何畸变问题耦合时的比例模型与原型物理量对应关系的描述。

1 薄壁圆管相似律分析

在结构冲击相似分析中，一般使用基于一组无量纲数的比例因子来预测比例模型的力学行为，如VSG 量纲体系或DLV 量纲体系，其比例因子如表1 所示。其中，比例模型和原型相关的物理量分别用下标m 和p 表示，β=/表示比例模型和原型相关物理量的比值，例如β=/表示比例模型和原型速度的比值，比例模型和原型的几何比例因子β=/。

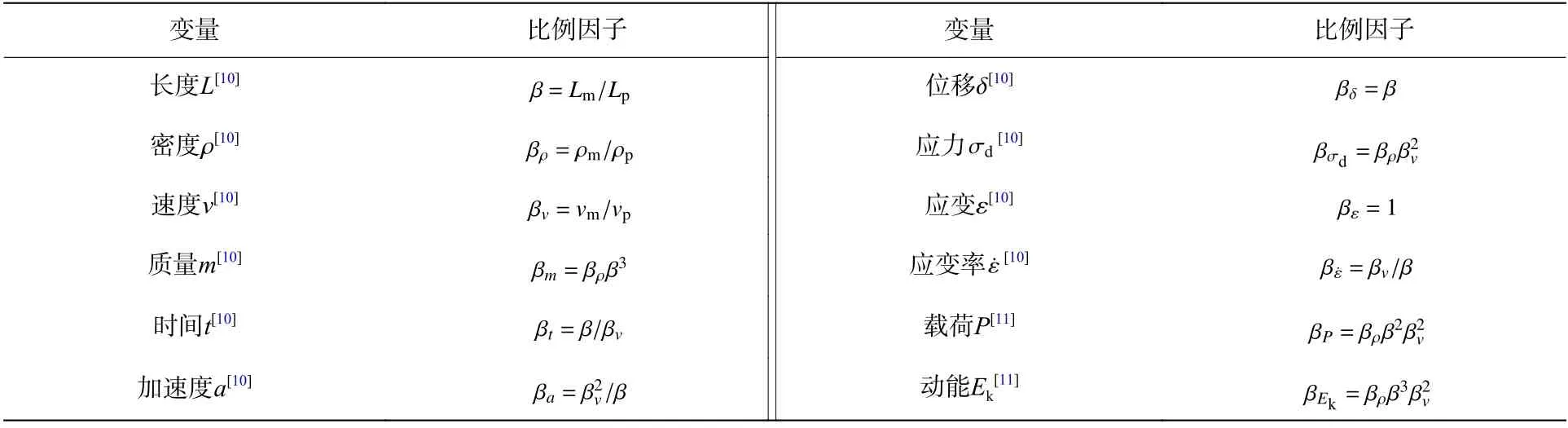
表1 纯几何相似律比例因子[10-11]Table 1 Scaling factors by pure geometric similarity[10-11]

基于表1 中的相似关系，目前针对受轴向冲击载荷作用的薄壁圆管的相似律研究对象均为纯几何缩放的比例模型，也就是说薄壁圆管的厚度、长度和半径服从同一个几何比例因子，亦即β= β=β =β。

但对于薄壁圆管而言，由于其自身几何尺寸的特性，厚度方向的尺寸与半径和长度方向的尺寸完全不在一个量级，厚度方向若要按照长度和半径的几何比例因子进行缩放，会导致比例模型加工的成本远远超过加工一个原型试验件的费用。并且，受到加工限制，其厚度方向的尺寸并不一定能够与长度和半径按照同一个几何比例因子进行缩放，这时就会产生几何畸变模型，这时，β= β= β =β 这一基础条件会遭到破坏，将会导致表1 中的相似律不能全部满足，这就需要重新推导薄壁圆管的相似律。

1.1 受轴向冲击的薄壁圆管塑性响应相似律分析

考虑到薄壁圆管的结构响应特性，以薄壁圆管压溃过程中的平均载荷、位移和能量这3 个响应变量作为相似设计的关键参数。影响薄壁圆管压溃特性的参量有：厚度、半径、长度、冲击速度、冲击质量、材料的密度ρ、流动屈服应力σ。

根据薄壁圆管理论，在推导过程中做如下假设：

（1）受轴向冲击载荷作用的薄壁圆管的变形模式服从Alexander 所给出的轴对称变形模式，如图1 所示；

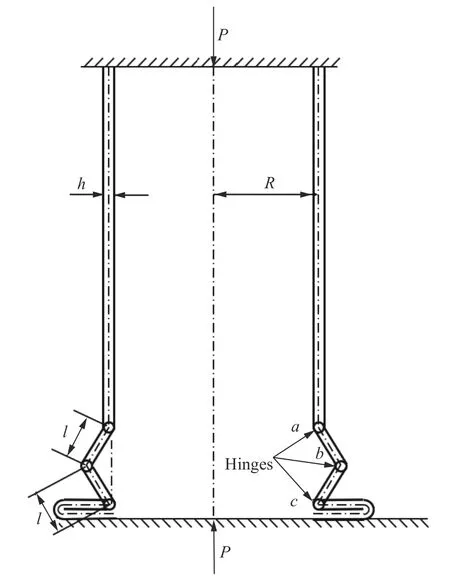
图1 轴向受压薄壁圆管的轴对称压溃模式Fig. 1 Axisymmetric crushing mode of the thin-walled cylindrical shell under axial compression

（2）薄壁圆管壁厚与半径及长度相比为小量，服从薄壳理论；

（3）与弹性变形相比，塑性变形占据主导地位，弹性变形可以忽略不计；

（4）薄壁圆管使用理想弹塑性材料，材料的流动屈服应力为一定值；

（5）薄壁圆管受到重撞击物的低速冲击；

（6）定义基本几何比例因子：β = β= β。

当薄壁圆管发生图1 所示的准静态压溃模式时，Alexander给出了该模式下的薄壁圆管每产生一个完整折皱时的平均压溃力和折皱长度的表达式：

式中：为冲击块的质量，为撞击物的初始速度。

将式（2）代入式（3）可得：

对于遵循图1 所示的压溃模式的薄壁圆管来说，在折皱的轴对称部分段，距离点径向距离为的微元伸长量为：

对应该微元处的环向应变为：

不难发现，图1 中段各点处的环向应变与成正比，那么对于一个完整折皱，∈[0,]，其平均环向应变为：

综上所述，得到受轴向冲击载荷的薄壁圆管的缩放比例因子，见表2，当比例模型与原型满足表2 中的比例因子时，比例模型可以准确地预测原型的动态响应。

表2 受轴向冲击的理想弹塑性薄壁圆管比例因子Table 2 Scaling factors of the elastic-ideal plastic thin-walled cylindrical shell under axial impact loading

1.2 考虑应变率效应和应变硬化效应的相似律分析

实际工程中，理想弹塑性的材料是几乎不存在的，绝大多数金属材料的塑性阶段都存在着应变率效应和应变硬化效应，如图2 所示，材料的流动屈服应力是应变和应变率的函数而非一固定值，即：

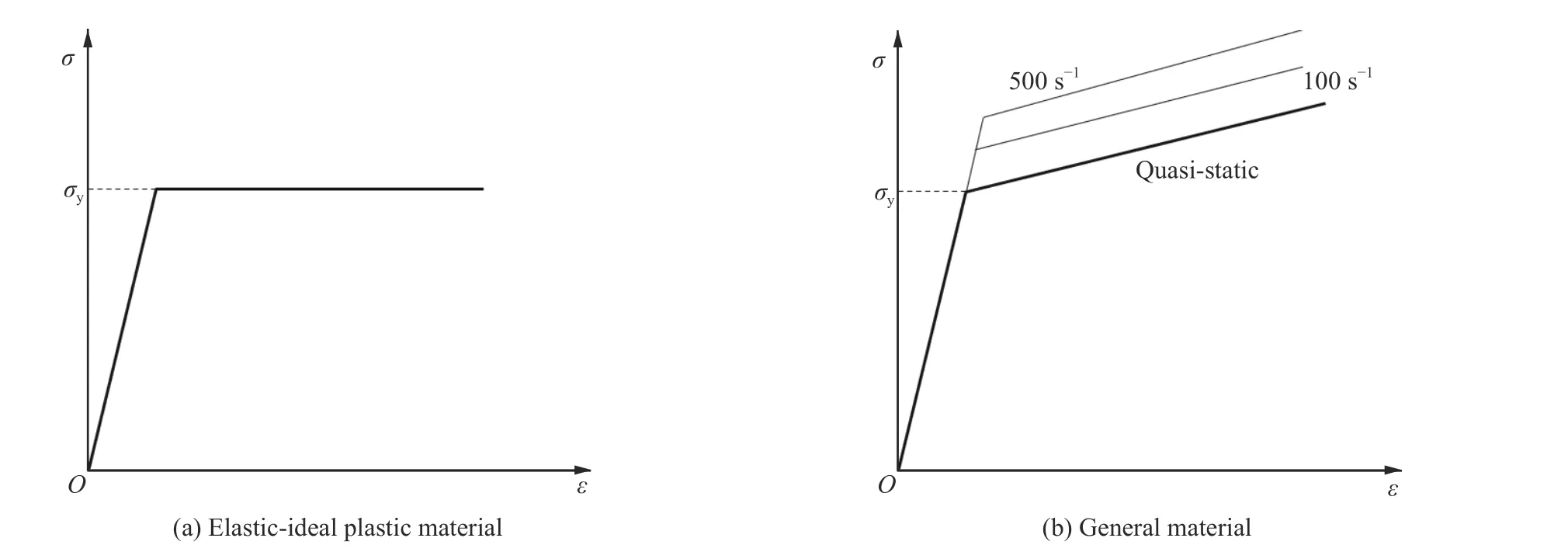
图2 金属材料应力-应变曲线Fig. 2 Stress-strain curves of metal materials

至此，我们将理想弹塑性假设下的薄壁圆管缩比相似分析拓展到了同时伴有应变率效应和应变硬化效应的一般材料薄壁圆管缩比相似分析的应用中。

2 数值验证

2.1 有限元模型

为了验证本文所推导的相似律对于结构缩比相似分析中的应变率和应变硬化效应畸变问题以及几何畸变问题的修正能力，在ABAQUS中建立了如图3 所示的薄壁圆管模型进行验证分析。薄壁圆管原型的长度=240 mm，中性面半径=60 mm，壁厚=1.8 mm。薄壁圆管材料选取应变率较为敏感的1006 钢，采用Johnson-Cook 本构模型进行数值模拟，材料参数见表3。

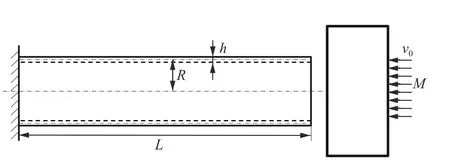
图3 受轴向冲击的薄壁圆管示意图Fig. 3 Schematic diagram of a thin-walled cylindrical shell under axial impact

表3 1 006 钢的材料参数[24]Table 3 Material parameters of 1 006 steel[24]

薄壁圆管采用CAX4R 轴对称单元进行仿真，锤头和地面则使用刚体单元。薄壁圆管自由放置于刚性地面上，顶部受到质量=128 kg、速度=12 m/s 的质量块冲击。薄壁圆管与地面之间的摩擦因数为0.2，圆管内壁、外壁之间设置为无摩擦。

分别建立了基本几何比例因子β=1/10，厚度方向的比例因子β分别为 0.12、0.15、0.18 和0.20 的比例模型。并按照表2 所给出的相似律获得速度修正比例因子，定义几何畸变度η = β/β。由表2 可得理想弹塑性材料的薄壁圆管几何畸变比例模型的各动态变量的比例因子，见表4。同时为了验证本文对于应变率和应变硬化效应与几何畸变效应耦合后的修正方法，建立了考虑应变率效应和应变硬化效应后的薄壁圆管几何畸变比例模型，并按照式(18)所给出的方法获得应变率区间和应变硬化区间上的最佳速度比例因子，通过表2 即可获得比例模型与原型各动态变量的比例因子，见表5。其中，应变率区间和应变区间在大量数值模拟经验的基础上分别选取为[0, 500]和[0, 0.6]。

表4 理想弹塑性模型几何畸变比例因子Table 4 Scaling factors of geometrically-distorted models of elastic-ideal plastic material

表5 考虑应变率效应和应变硬化效应几何畸变模型比例因子Table 5 Scaling factors of geometrically-distorted models considering strain-rate sensitivity and strain hardening

2.2 结果分析

2.2.1 理想弹塑性几何畸变模型结果分析

图4 为使用本文提出的受轴向冲击的薄壁圆管几何畸变修正方法后，获得的修正后理想弹塑性薄壁圆管的几何畸变比例模型与原型结构动态响应时间曲线的对比。图4(a)为锤头的速度-时间响应曲线，图4(b)为薄壁圆管首个折皱处塑性铰位置的等效塑性应变-时间响应，图4(c)、(d)分别为锤头的位移和能量-时间响应曲线，图4(e)为薄壁圆管几何畸变比例模型与原型载荷时间-曲线的对比。表6 为修正后的薄壁圆管几何畸变模型所预测原型的峰值位移和平均载荷与原型响应之间的相对误差。

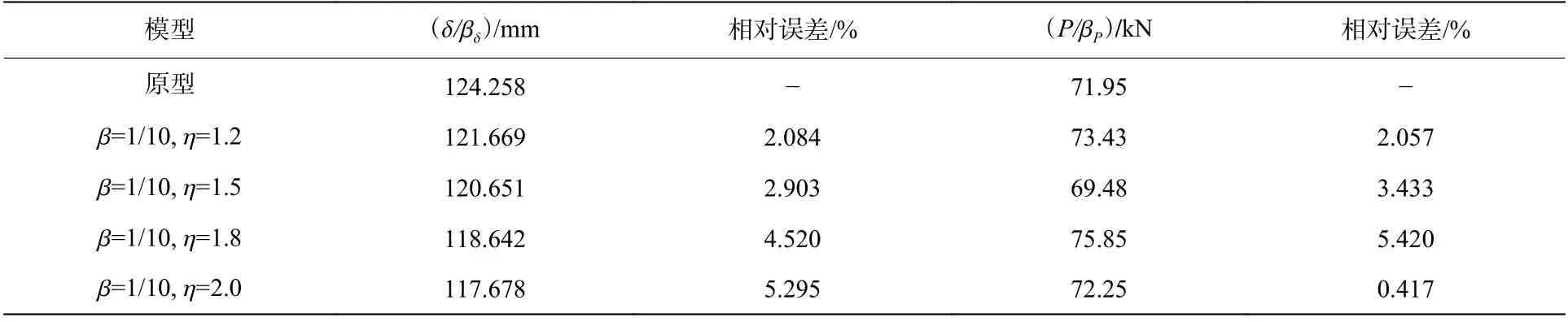
表6 比例模型与原型的峰值位移和平均载荷相对误差Table 6 Relative errors in the peak displacement and average force between the scale models and prototype

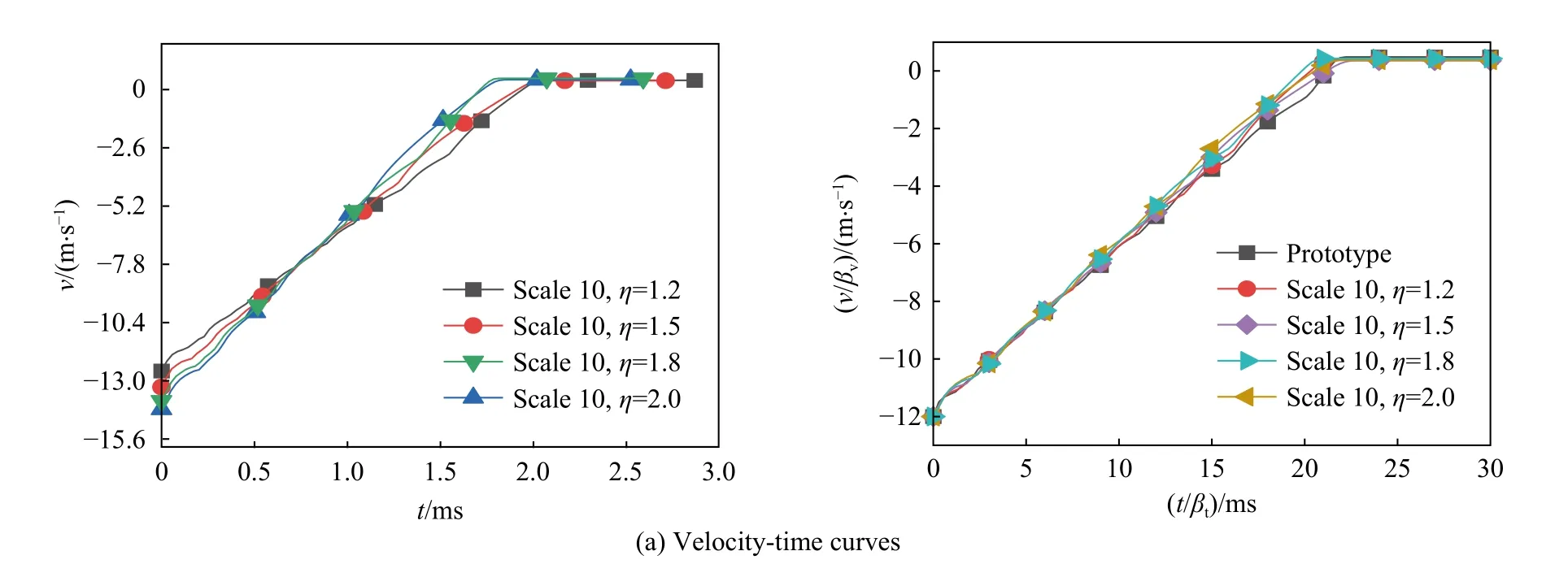
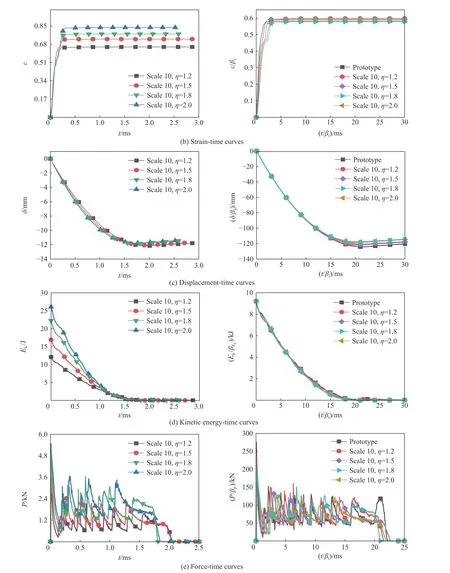
图4 原型与比例模型的动态响应-时间曲线Fig. 4 Dynamic response-time curves of the scale models and the prototype

从图4 可以看出，修正前的不同几何畸变度的理想弹塑性薄壁圆管比例模型的响应曲线基本无法重合，各条曲线上的相应点所对应的时间与值均不相等，而修正后的理想弹塑性薄壁圆管几何畸变比例模型与原型的速度、能量、位移、等效塑性应变和载荷-时间曲线重合性明显改善，修正后的比例模型的速度和应变-时间曲线与原型的响应曲线完全重合。对于本文推导过程中的3 个关键设计参数：能量、位移δ 和平均载荷，修正后的比例模型的位移和能量曲线与原型的响应曲线重合性也非常好，但是修正后的比例模型与原型的载荷-时间曲线重合度不是很高。这是因为本文推导的相似律以能量、位移δ 和平均载荷作为关键相似设计参数，薄壁圆管的折皱长度与位移δ 并不服从同一个比例因子，因此几何畸变比例模型与原型的折皱数量并不一致，导致修正后的比例模型和原型的载荷-时间曲线无法完全重合，但是相较修正前，其误差已经大大减小，且其整体的时间趋势一致性比较良好。因此我们又分析了比例模型与原型的峰值位移和平均载荷的误差，从表6 可以看到，即使几何畸变度达到2，比例模型所预测的结果与原型的峰值位移和平均载荷的相对误差均不超过6%。

综上所述，使用本文所推导的相似律，修正后的理想弹塑性薄壁圆管几何畸变比例模型的动态响应可以准确地预测原型的动态响应。

2.2.2 考虑应变率效应和应变硬化效应几何畸变模型结果分析

使用本文提出的受轴向冲击的一般材料薄壁圆管几何畸变修正方法，同时考虑应变率效应和应变硬化效应与几何畸变问题，获得的修正后比例模型预测结果与原型动态响应时间曲线的对比如图5 所示。图5(a)为锤头的速度-时间响应曲线，图5(b)为薄壁圆管首个折皱处塑性铰位置的等效塑性应变-时间响应，图5(c)、(d)分别为锤头的位移和能量-时间响应曲线，图5(e)为修正前后的薄壁圆管几何畸变比例模型与原型载荷时间-曲线的对比。表7 为考虑应变率效应和应变硬化效应，修正后的薄壁圆管几何畸变模型所预测原型的峰值位移与平均载荷与原型响应之间的相对误差。

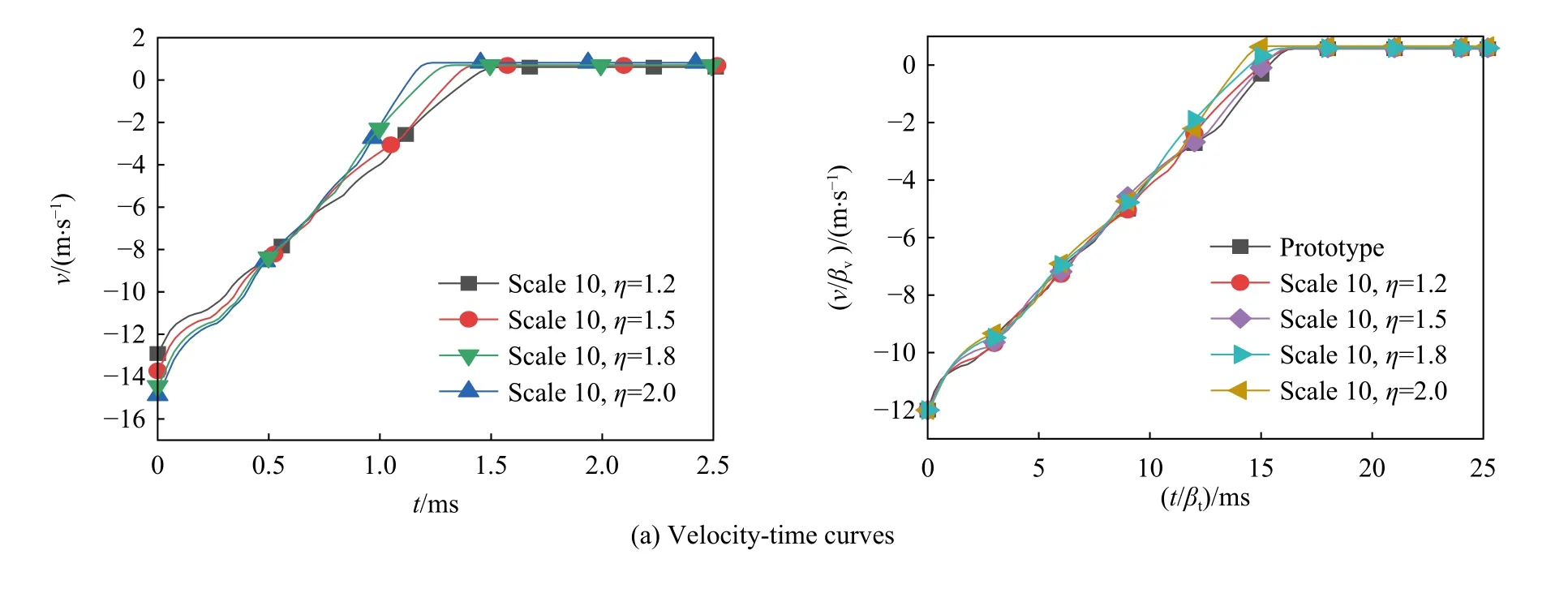
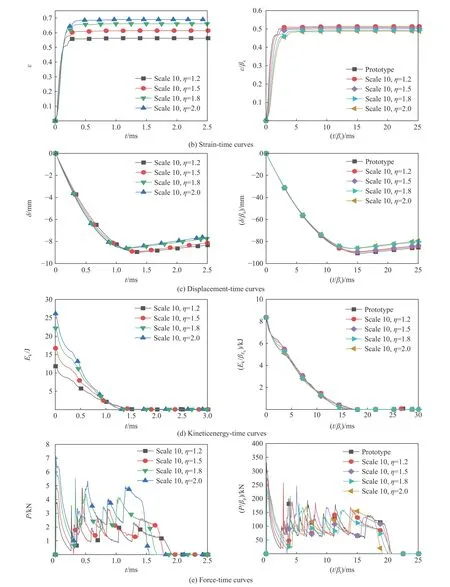
图5 修正后的比例模型与原型的动态响应-时间曲线Fig. 5 Dynamic response-time curves of the modified scaled models and the prototype

从图5 可以看出，修正前的不同几何畸变度的一般材料薄壁圆管比例模型的响应曲线基本无法重合，各条曲线上的相应点所对应的时间与值均不相等，而修正后的一般材料薄壁圆管几何畸变比例模型与原型的速度、能量、位移、等效塑性应变和载荷-时间曲线重合度明显提高。修正后的比例模型的速度和应变-时间曲线与原型的响应曲线基本完全重合。对于本文推导过程中的3 个关键设计参数：能量、位移δ 和平均载荷，修正后的比例模型的位移和能量曲线与原型的响应曲线重合度非常高，但修正后的几何畸变比例模型的载荷-时间曲线与原型重合度不是很高，原因如2.2.1 节所述。然而随着几何畸变度的增大，修正后的比例模型的动态响应变量曲线与原型的动态变量响应曲线的重合程度逐渐降低。对比修正后的比例模型与原型的峰值位移和平均载荷，从表7 中可以看到，即便几何畸变度增大至2，比例模型所预测的结果与原型的峰值位移相对误差依然不超过6%，平均载荷的误差亦不超过8%。

表7 考虑应变率与应变硬化效应的比例模型位移与平均载荷相对误差Table 7 Relative errors in the peak displacement and average force of the scaled models considering strain-rate sensitivity and strain hardening

可见，通过使用本文所推导出的薄壁圆管相似律，对考虑应变率效应和应变硬化效应的一般材料薄壁圆管几何畸变比例模型进行修正后，比例模型可以准确地预测原型的动态响应。

3 结 论

以受轴向冲击载荷的薄壁圆管为研究对象，基于量纲分析与方程分析，推导了薄壁圆管结构的几何畸变相似律。

（1）通过能量守恒定律，直接建立了结构几何特征与冲击速度和冲击质量的关系，解决了理想弹塑性材料薄壁圆管的壁厚、半径和长度非等比例缩放的不相似问题。

（2）建立应变区间和应变率区间上比例模型预测的流动屈服应力与原型流动屈服应力的最佳逼近关系，解决了考虑材料应变率和应变硬化效应与薄壁圆管几何畸变问题耦合时的不相似问题。

（3）通过数值模拟验证了该方法的有效性，研究表明，使用该方法可大幅降低几何畸变模型预测结果与原结构实际响应的误差，特别是轴向冲击问题备受关注的载荷和能量，相似误差最大不超过8%。

但该相似律只适用于几何畸变比例模型满足薄壳假设且弹性变形能占比可忽略时的薄壁圆管几何畸变相似性分析，对于不满足该条件的薄壁圆管相似性分析还需进一步研究。