考虑作业疲劳的物料搬运路径研究

陈晶晶，方叶祥，王文凤 CHEN Jingjing,FANG Yexiang,WANG Wenfeng

（南京工业大学 经济与管理学院，江苏 南京 211816）

0 引言

虽然如今作业人员辅助自动化设备作业已成为重要的生产方式，大量的机械化生产代替了手工作业，但是在进行距离较短、重量相对较轻的情况下，大部分企业还是将手工搬运作为搬运作业的首要选择。企业在进行手工搬运作业时往往更加注重效率，所以一般会考虑作业人员行走路径最短，例如Nip等为了行走路径和加工时间最小化，研究了最短路径和流水线车间搬运组合问题，并提出了近似算法；刘凯等在U型线平衡问题中考虑了作业人员作业时间随机分布与作业人员行走路径时间。Range等为解决作业人员负责多机器且机器加工能力有限问题中考虑了作业人员的行走路径。上述文献研究行走路径问题是为了缩短搬运时间，提高企业经济效益。

然而手工搬运作业（Manual Materials Handling，MMH）是一种长时间、高强度的作业类型，作业人员长期进行手工搬运作业容易引起作业疲劳。郭伏、吕伟等用主观疲劳量表、表面肌电和心电指标实验证明作业者的搬运时间、搬运负荷与作业疲劳之间有很强的线性关系；任笑影等通过人因仿真模拟分析静态任务中的受力情况和动态搬运过程中的肌肉变化规律，得出在搬运过程中人体会有大量的能量消耗，容易引起作业疲劳；BATTINI等以能量消耗值为人体疲劳的量化评估指标，分析了装配线平衡问题，并指出较高作业负荷的工作会导致疲劳的显著增加；张文倩等在手工搬运作业中考虑到投入材料数量和生产工序对搬运时间和能量消耗的影响，研究表明搬运时间变化率与能量消耗变化率呈负相关；于瑞峰等在手工装配作业中将人的因素和物流因素相结合进行优化，在保证生产高效率的情况下，减轻作业者的劳动强度。

上述文献对优化手工搬运作业流程的研究尚未见最短路径和人体作业疲劳相结合考虑，同时优化效率和缓轻疲劳。为此本文根据搬运负荷、搬运时间与作业疲劳之间的关系，建立时间和疲劳双目标优化函数，采用NSGA-Ⅱ进行求解，将结果与传统模型进行比较，以验证本文模型的可行性和优越性。

1 问题描述和模型构建

1.1 问题描述。本文研究在一个搬运中心配有m位搬运作业人员，且每人的额定负荷为Q，作业人员将n种物料搬运至存储中心的n个存储点进行对应存储，要求综合考虑费用、时间和负荷因素，作业人员在保证搬运效率的同时还能大幅度降低作业疲劳，对该问题进行多人搬运路径规划优化研究，搬运存储方式如图1所示。

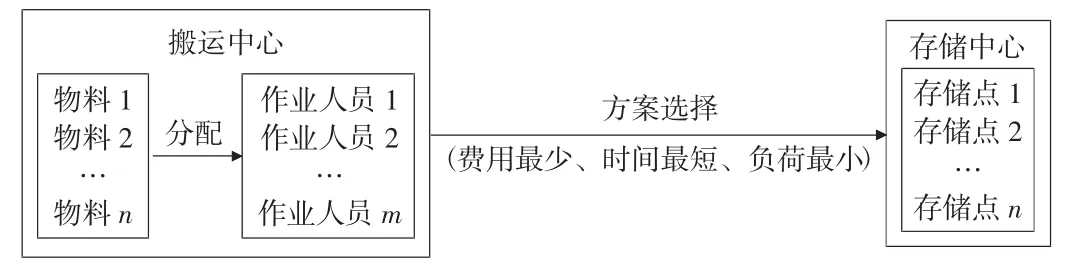
图1 搬运存储结构

1.2 模型构建

1.2.1 模型构建的参数与变量说明。N表示搬运的存储点数；（N=0,1,2,…,n；0代表搬运中心，1,…,n代表存储点）；k表示搬运中心作业人员数；（k=1,2,3,…,m）；Q表示搬运作业人员的最大载重量；g表示存储点i搬运量；c表示存储点i和存储点j之间单位距离的搬运费用；d表示存储点i与存储点j之间的距离；v表示作业人员从存储点i到存储点j的搬运速度，当i=j时，v=0；t表示作业人员k在存储点i的停留时间；x表示第k作业人员从第i点搬运至j点，取值为1，未经过取值为0；y表示第i个存储点由第k作业人员配送，取值为1，否则为0。

1.2.2 目标函数。作业人员在进行手工搬运作业时特别容易产生作业疲劳，手工搬运作业是引起肌肉骨骼疾患的重要原因，因此企业想要提高手工搬运效率，考虑作业人员的作业疲劳这一因素至关重要。为了将问题更加贴近实际情况，要将人体疲劳因素考虑进模型中，其中吕伟用主观测量、面肌电测量和心电测量等实验数据处理后证明作业者的搬运时间和搬运负荷对疲劳有显著的影响，并且运用回归分析得出搬运负荷、搬运时间与疲劳之间有很强的线性关系，因此可以建立有关搬运时间和搬运负荷的疲劳函数，即：疲劳-α*搬运时间*搬运负荷。根据以上分析建立搬运费用C最小和作业疲劳E最小为优化多目标函数：

约束条件主要包括以下内容：

约束式（3）、式（4）表示变量的定义，即为确保m位作业人员从同一搬运中心出发，搬运完一定数量的存储点并且每存储点只能被其中一位作业人员进行搬运配送，完成所有物料的搬运最后返回到搬运中心，约束式（5）表示每个存储点只能有一位作业人员配送；约束式（6）、式（7）表示存储点作业人员的唯一性；约束式（8）搬运任务覆盖所有存储点；约束式（9）表示每条搬运路线上存储点的需求量之和不超过作业人员最大载重量。

2 模型求解

上述模型属于双目标函数问题，在合理时间内很难利用传统的数学规划方法求解出答案，为解决双目标函数问题时通常利用双目标遗传算法有较好的效果，其中由Deb等提出的NSGA-Ⅱ对于求解双目标函数问题效果显著，带精英策略的非支配排序遗传算法，用拥挤度代替适应值共享，提高了计算效率。因此文中采用该算法对多人搬运路径的双目标优化模型进行求解。

2.1 染色体编码。本文主要是采用自然数形式的两部分染色体进行染色体编码。即染色体的第一部分表示需要搬运的所有存储点的一种排列，而第二部分则为第一部分的一种分割，分割后的结果为不同作业人员的搬运行走路径，如图2所示：

图2 两部分染色体编码方式示意

2.2 初始化。随机选择一些数量的个体组成最初的种群，记为初始种群P。

2.3 适应度函数。适应度函数能够反映出每一种解与最优解之间的差距，通常适应度函数是由目标函数转化而来。本文所求目标函数是最小化搬运成本、搬运时间和搬运负荷，因此本文的目标函数值越小，适应度函数则越高。

2.4 选择、交叉、变异算子。在第t代，将种群P随机生成两种N个数的排列，本文主要采用二元锦标赛选择机制来选择算子，选择出N个需要交叉的父代个体，随后对染色体进行交叉和变异操作，产生长度为N的子代种群Q。

2.5 非支配排序。将父代种群P和子代种群Q合并，记为R。随后对R执行非支配排序使得种群被划分为r个非支配集合F,F,…,F；将非支配集合按照等级依次整合到新的种群P中，直至第i个集合F并入种群后长度大于或等于N，对前i个进行拥挤距离排序，并将F依据拥挤距离由大到小降序排列，将排序后靠前的个体并入种群中，从而组成新的大小为N的新种群。

2.6 终止。如果满足终止条件，则程序结束，否则，令t=t+1，跳转至2.4。

3 算例分析

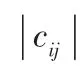
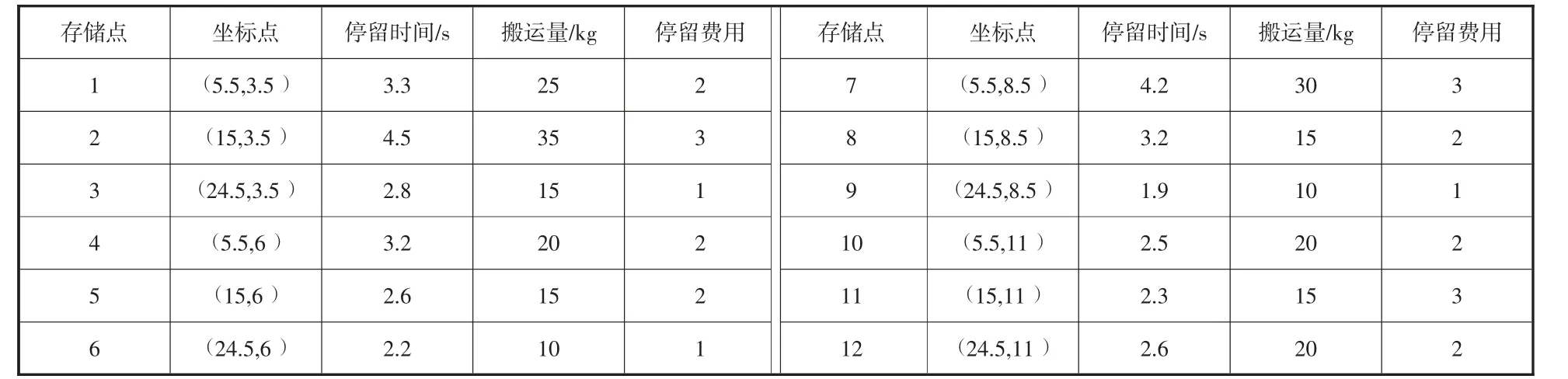
表1 各存储点的位置和搬运量

3.2 求解结果。根据建立的数学模型和以上数据，对双目标函数模型进行求解，设定初始种群规模为100，迭代次数为100，交叉概率为0.9，变异概率为0.1，其中搬运疲劳目标函数中的α取值为1。求解出的最优解集如表2所示，Pareto最优解集如图3所示。

表2 最优解集

图3 Pareto最优解集分布

模型的Pareto最优解集共有5个方案，根据表2、图3综合选择，从5个方案中选取出2个优化后的搬运路径和原始搬运路径进行对比，如表3所示：

表3 优化前后路径对比

由表3得出：模型优化后的搬运路径在搬运费用和搬运负荷上均有明显降低，因此验证所建模型对提高企业经济效益和降低作业人员的作业疲劳具有可行性。

3.3 对比分析。为验证本文模型的优越性，根据传统情况建立最小化搬运成本和搬运时间多目标传统模型，约束条件与本文模型一致，传统模型及求解结果如表4所示。

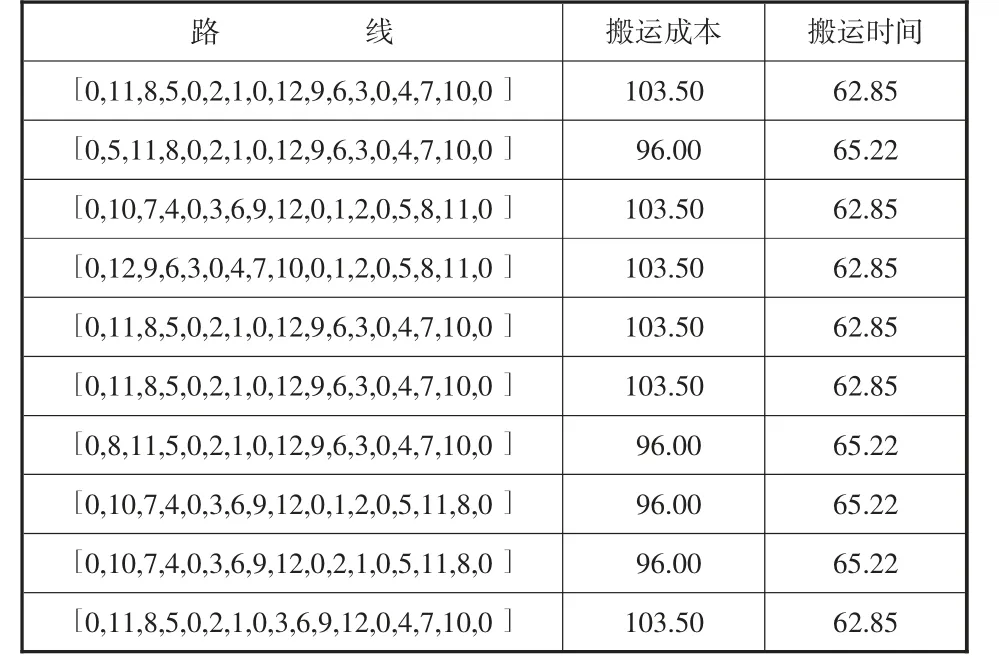
表4 传统模型最优解集

根据表4、图4综合可以选取出传统模型中2个优化后的搬运路径和原始搬运路径进行对比，如表5所示。

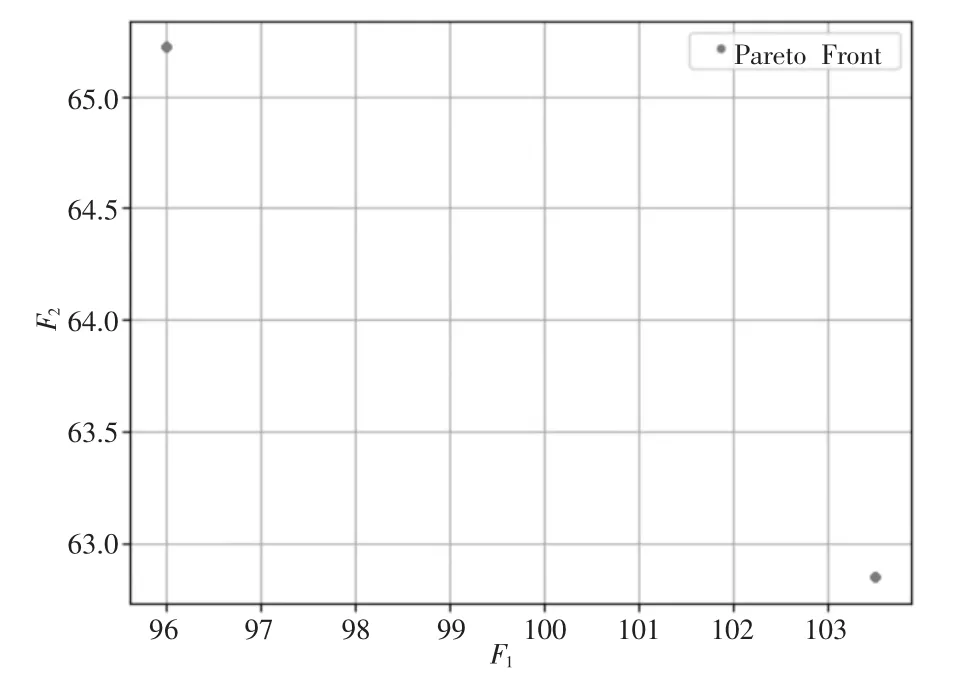
图4 传统模型的Pareto最优解集分布

表5 传统模型优化前后路径对比

由表5得出：传统模型优化后的搬运路径在搬运费用和搬运时间上均有明显降低，因此可以验证所建传统模型对提高企业的搬运效率和经济效益具有可行性。

传统模型与本文模型的目标函数有所不同，因此两个模型的最优解集不能直接进行比较。为体现本文模型的优越性并且使两个模型的最优解集能直接比较，考虑将传统模型的最优解集带入本文模型中求解出最小化搬运负荷，本文模型的最优解集带入传统模型中求解出最小化搬运时间，分别如表6、表7所示；最后在两个模型的最优解集中分别选择其中一个解进行对比分析，如表8所示。

表6 传统模型的最小化搬运成本、搬运时间、搬运负荷

表7 本文模型的最小化搬运成本、搬运时间、搬运负荷

表8 结果对比分析

总的来说，两个模型进行对比分析后，本文模型在搬运成本和搬运时间稍有增加的情况下，基本能够满足搬运效率和经济效益不变，显著地降低作业人员的搬运负荷，从而有效地减轻作业人员的作业疲劳。

4 总结

本文为提高搬运效率和缓轻作业疲劳，解决在手工搬运作业问题中只注重搬运效率而忽视作业疲劳问题，提出了一种可以兼顾搬运效率和作业疲劳的双目标优化模型，同时在模型中对作业人员的搬运负荷进行约束，使问题更加贴近现实。本文模型在基本满足搬运效率和经济成本不变的情况下，还能显著地降低作业人员的搬运负荷，从而有效的缓解作业人员的作业疲劳。