浅海天然气管道泄漏扩散过程模拟研究

李延豪，侯磊，于巧燕，柴冲，肖开喜

浅海天然气管道泄漏扩散过程模拟研究

李延豪1,2，侯磊1,2，于巧燕1,2，柴冲1,2，肖开喜1,2

（1.中国石油大学（北京） 机械与储运工程学院，北京 102249； 2.中国石油大学（北京） 油气管道输送安全国家工程实验室，北京，102249）

为评价浅海海底天然气管道泄漏事故后果，根据计算流体力学与多相流动理论，针对国外某天然气管道海峡穿越段，建立浅海海底管道泄漏扩散过程的计算模型。将泄漏孔径、泄漏速率、水流速度3个主要影响因素作为条件变量，模拟不同情况下的气液两相运动过程。结果表明，水下气体扩散分为三个阶段，即泄漏口上方形成气团、气团呈蘑菇状上升、气团由大气泡分裂为小气泡；泄漏孔径和泄漏速率对水下气体扩散到水面的时间具有显著影响，泄漏孔径与泄漏速率越大，气体泄漏量越大；气体泄漏量越大，水下气团体积越大，到达水面的时间越短；水流速度显著影响气体的扩散轨迹，水流速度越大，气体运动轨迹与海底的夹角越小，沿海流方向扩散的距离越远。研究结果可为水下天然气管道泄漏事故应急处理提供一定的科学指导。

海底管道； 气体泄漏； 多相流动； 计算流体力学

海底管道具有输量大、效率高的优点，是海上油气最主要的输送方式。不同于陆上埋地管道，海底管道每时每刻都遭受着海流的冲刷及海底地震、台风等自然条件的威胁，加之海水腐蚀、第三方破坏等因素，海底管道的安全性和完整性面临巨大的考验[1]。海底天然气管道一旦发生泄漏，其扩散至海面的可燃气体有可能导致爆炸、火灾等重大事故，严重威胁海上工作人员和生产设施的安全[2]。因此，掌握海底管道天然气泄漏扩散规律，确定气液两相在不同环境条件下的运动分布，对海底天然气管道的风险防范管控及事故应急处理具有重要意义。

目前，关于水下气体泄漏扩散的研究多基于气泡羽流理论[3⁃5]。国内学者多数以气泡羽流理论模型为参考，运用有限元软件进行仿真，并辅以一定的实验验证，对已有的研究成果进行重现及进一步完善。景海泳等[6]采用VOF多相流模型和DPM离散相模型耦合的方式进行数值模拟，得到了气泡粒子的扩散半径和轴向位移，但模拟气体的泄漏量较小，没有考虑到水流速度对水中气泡运动的影响，也未考虑水下气体的可压缩性。文闯等[7]采用VOF多相流模型进行数值模拟，考虑了水下泄漏气体的可压缩性，通过实验验证了模拟结果的准确性和可靠性，但是仍以静水条件作为模拟设置，不符合海底管道实际工作环境的特点。窦梓元[8]在数值模拟的基础上，通过无量纲分析得出泄漏气体的上浮时间、水平迁移距离与管道压力、水流速度、泄漏孔径的无量纲关系。李新宏等[9]对水下气泡的运动轨迹进行跟踪求解，并以水下气体扩散结果作为依据，分析了天然气在大气中的扩散。王少雄等[10]通过建立三维CFD模型和积分数学模型，研究了水下输气管道泄漏扩散特性，并对两种模型预测结果的准确性进行了对比评估。综上所述，国内已有研究对不同条件下天然气管道泄漏气体运动分布规律的多因素分析仍不完善。因此，针对国外某天然气管道海峡穿越段，本研究以泄漏口孔径、泄漏速率和水流速度为变量，运用Fluent软件对水下泄漏扩散气体的时空分布进行有限元数值模拟，分析不同条件下浅海海底管道泄漏气体的扩散规律。

1 海底天然气管道泄漏扩散理论模型

1.1 基本控制方程

流体流动遵循质量、动量和能量守恒定律，对这3个守恒方程进行整合，其表达式如式（1）所示[11]。

1.2 湍流模型

选用标准⁃湍流模型对气液两相运动过程进行求解，其输运方程为[12]：

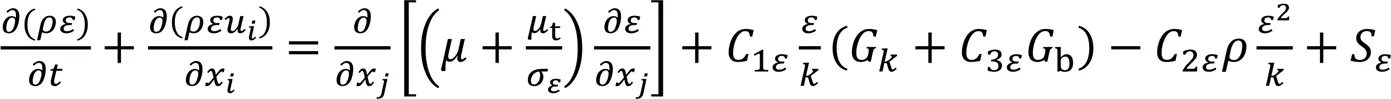
1.3 VOF模型

VOF多相流模型在欧拉坐标系下，通过求解基本控制方程及每个网格内的流体体积分数来进行相间流体的表面跟踪[13]。

每个单元的流体体积分数F[14]：

式中，为相，取1或2；F=0为单元内无该相流体；0<F<1为单元内既存在该相流体又存在其他相流体；F=1为单元内充满该相流体。

F满足如下输运方程：

式中，、分别为流体在和方向的流动速度，m/s。

2 浅海天然气管道泄漏扩散仿真模型

2.1 网格模型

以国外某天然气管道海峡穿越段为研究对象，该输气管道管径为1 016 mm，输送压力为9.8 MPa。为了简化数值模型，取实际工程穿越段的最大水深22 m作为管道数值模型的水深，忽略海底地形因素的影响。受水体运动的影响，泄漏气体在沿海流方向具有水平最大扩散距离，因此选取沿海流方向的垂直切面为研究平面。根据预先模拟结果，在22 m水深条件下泄漏气体上浮到水面的过程中，沿海流方向的最大扩散距离不超过30 m，最终选择长40 m、宽22 m的矩形建立二维几何模型，泄漏孔位于模型底部距离左侧10 m处（见图1）。采用结构化网格划分方法，相比于非结构化网格，整个数值模型的网格数量更少，更有利于计算结果的收敛[15]。考虑到泄漏口处气体与水体的相互掺混属于剧烈、复杂的湍流运动，对泄漏口及气泡扩散区域的网格进一步细化加密以防止计算结果发散。

图1　二维网格模型

2.2 边界条件设置

计算域底部的气体泄漏口设置为速度入口，底部其余边界设置为无滑移的壁面。顶部边界作为水的自由表面，设置为自由出流边界。在静水条件时，计算域左右两侧边界均设置为自由出流；考虑水流速度对气体扩散的影响，计算域左侧采用速度入口，通过UDF函数定义水流速度随深度的变化规律，计算域右侧仍采用自由出流边界。

2.3 条件变量设置

以国外某天然气管道海峡穿越段重现期1年的海流速度作为实际水流速度（见表1），拟合出水流速度随水深变化的公式（见式（7））：

式中，v为距海底高度处的海流流速，m/s；为距海底的高度，m。

以静水条件和实际水面流速的2倍（2.72 m/s）设置对照组。2倍水面流速情况下不同深度的水流速度按式（8）求得[20]：

式中，v为海面流速，m/s；为水深，m。

表1　不同深度处的海流速度

根据不同的泄漏孔径、泄漏速率和水流速度，设置多组模拟工况进行计算，详细条件变量设置如表2所示。

表2　条件变量设置

2.4 求解器设置

选用非稳态压力基求解器，采用双精度模式提高计算结果的精确性。操作条件中勾选重力选项，考虑重力对流体运动的影响，选取VOF多相流模型和标准湍流模型作为基本计算模型，运用VOF模型中的隐式体积力公式，提高迭代计算的稳定性[21]。选择PISO算法作为求解器的压力⁃速度耦合方式，相比其他类型的非稳态求解算法，PISO的残差收敛更稳定，求解速度更快[22⁃24]。

3 数值模拟结果及分析

3.1 水下扩散过程分析

对国外某天然气管道海峡穿越段的实际情况进行探讨，即泄漏孔径60 mm，泄漏速率260 m/s，水流速度为实际海流速度。

不同时刻气液两相体积分数云图见图2。由图2可以看出，在泄漏初始阶段，天然气在管道内压的作用下从泄漏口喷射进海水中，高速气体因海水的阻碍在泄漏口上方急剧减慢，被海水包裹形成气团。气团中心部分天然气上升较快，两侧因回流作用上升较慢，导致气团呈现蘑菇状（见图2（a）），并在海流的作用下开始往右偏移。随着泄漏的进行，后续的泄漏气体不断地对上方的气团进行动能和体积的补充，在浮力的作用和下方气体的推动下，气团继续向上运动，体积也缓慢变大，强烈的湍流作用将蘑菇状气团逐步分裂为多个块状气团（见图2（b））。海水压力的不断降低使气团不再容易聚集，在气液两相之间不断地摩擦和掺混下，块状气团分裂得越来越小，两相间的相互渗透越来越强。气团的持续向上运动引起两侧海水的回流，使两侧的外部气团在运动过程中伴随着一定程度的旋转，气体的扩散范围越来越大（见图3）。此外，越往上运移海流的速度越来越大，海流冲刷作用的增强使大气泡进一步分散成许多小气泡，并进行大范围扩散（见图2（c））。泄漏发生5.5 s后，气体上浮至水面，此时的水平最大扩散距离约为20 m（见图2（d））。经对比可知，整个扩散过程的气液两相分布与气泡羽流模型基本一致。

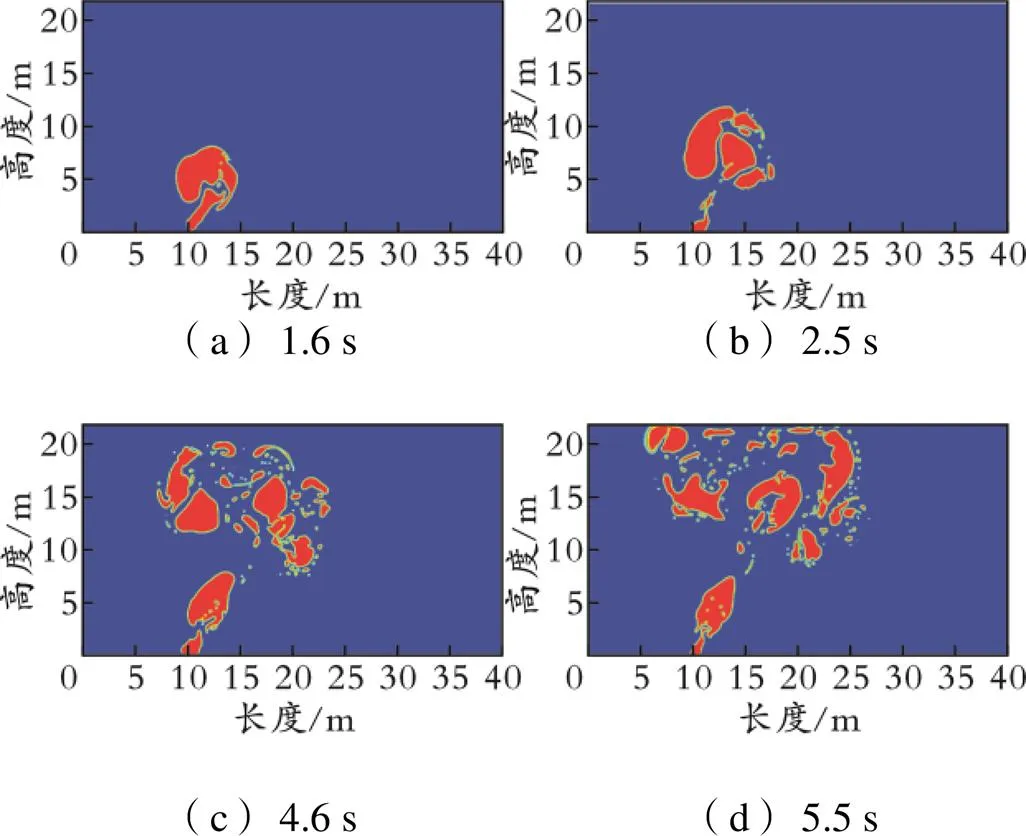
图2　不同时刻气液两相体积分数云图

图3　4.6 s时泄漏气体左右两侧水流流线

3.2 泄漏孔径的影响

选取气体泄漏速率为260 m/s、水流速度为实际海流速度，分别对10、30、60、80、100 mm孔径下的气体扩散过程进行模拟，结果见图4。不同泄漏孔径下气泡上升高度随时间变化的曲线见图5。

图4　泄漏孔径不同时气体扩散至海面的气液两相体积分数云图

图5　不同泄漏孔径下气泡上升高度随时间的变化

由图4、5可知，泄漏孔径为10、30 mm时，泄漏口处气体以少量小气团和较多小气泡的形式存在，小气团在向上扩散的过程中又分裂为许多小气泡。因泄漏量较少，下部气团对上方气团的补充不足，导致气团的体积小,从而受到的浮力小，上移速度较慢，最终分别于7.1、6.0 s时扩散至海面；当泄漏孔径增大至60、80、100 mm时，由于泄漏量变大，气体主要以大气泡的形式存在，上浮过程中大气泡与海水掺混逐步分裂出大量的小气泡。因气团体积较大，引起的回流作用较为强烈，泄漏气体的左右两侧气泡出现了明显的旋转现象，上部气团不断受到下部气团动能和体积的补充，导致气体上移速度较快，分别于5.5、4.9、4.1 s时扩散至海面。由图5还可以看出，随着泄漏孔径的增大，气泡上升得越快，到达水面的时间越短。

3.3 泄漏速率的影响

以实际海流速度建立流场，取60 mm泄漏孔径，经计算该管道天然气的泄漏速率约为260 m/s，并以其0.25、0.50、0.75、1.25倍，即65、130、195、325 m/s设置对照组，对5种泄漏速率下的气体扩散过程进行研究。不同泄漏速率下气体扩散至海面时气液两相体积分数云图见图6，气泡上升高度随时间的变化曲线见图7。

图6　不同泄漏速率下气体扩散至海面时气液两相体积分数云图

由图6、7可知，泄漏发生1.0 s时，相同孔径下气体泄漏速率越大，泄漏口上方的初始气团体积越大，5种泄漏速率下的气团直径分别为2.3、3.0、4.0、4.8、5.0 m。在水下扩散的过程中，泄漏速率为65、130 m/s的气体主要以小气团的形式存在，而泄漏速率为195、260、325 m/s的气体均以块状气团和大气泡的形式存在。泄漏速率越大，气团初始动能越大，泄漏过程中上部气团受到下部气团动能的补充越大；泄漏速率越大，气体泄漏量越大，导致水中气团体积越大，受到浮力的作用也越大。同时，动能和体积两方面的影响使气团引起的回流作用更为强烈，泄漏气体的左右两侧出现了明显的旋转现象。随着泄漏速率的增大，气泡上升得越快，到达水面的时间越短，5种泄漏速率下的气团分别于7.0、5.8、5.7、5.5、4.5 s上升至海面。

图7　泄漏速率不同时气泡上升高度随时间的变化

3.4 水流速度的影响

由于受不同季节海面风向、洋流流向的变化以及海底地形的起伏等诸多因素的影响，实际的海洋流场较为复杂，只能对其简化进行模拟。以60 mm泄漏孔径和260 m/s泄漏速率为基准，选取静水条件、实际海流速度以及2倍水面流速进行计算，对得到的海流速度场进行模拟。图8为不同水流速度下气体扩散至海面时气液两相体积分数云图。

图8　不同水流速度下气体扩散至海面时气液两相体积分数云图

由图8可知，由于静水条件下的气体在水中只受浮力的作用，水平方向的扩散分布较为对称，最终以5.2 s上升至海平面，此时的水平最大扩散距离约为22 m，单侧气体距泄漏口的最大水平距离约为10 m。在水流速度的影响下，气体不仅受到浮力的作用，还受到左侧水流的作用。由于实际工况下的水流速度较小，气体所受浮力的影响大于左侧水流的影响，气体主要向上部空间扩散，扩散轨迹与海底的夹角较大。上部气体最终以5.5 s上升至海平面，此时的水平最大扩散距离为20 m，最右侧气体水平运动距离约为16 m。在水面流速为2倍的海流流场下，左侧水流对气体的推动作用较强，主要向斜上方进行扩散，扩散轨迹与海底的夹角较小。气体最终以5.2 s上升至海平面，此时的水平最大扩散距离约为23 m，最右侧气体距泄漏口的水平最大距离约为22 m。根据3种水流速度下的模拟结果发现，水流速度越大，气体受水流的推动作用越明显，气体运动轨迹与海底的夹角越小，沿海流方向的水平运移距离越大，而气体上升到水面的时间与水流速度并无明显关系。

4 结 论

针对国外某天然气管道海峡穿越段，根据计算流体力学与多相流动理论，建立浅海海底管道泄漏扩散过程的计算模型。以泄漏孔径、泄漏速率和水流速度为条件变量，运用Fluent软件进行有限元数值模拟，得出以下结论：

（1）分析不同时刻的气液两相体积分数云图，发现水下气体扩散分为三个阶段，即泄漏口上方形成气团、气团呈蘑菇状上升、气团由大气泡分裂为小气泡，模拟结果与气泡羽流模型的描述基本一致。

（2）分析各个对照组的模拟结果，发现泄漏孔径和泄漏速率对水下气体扩散过程具有显著影响。泄漏孔径与泄漏速率越大，气体泄漏量越大，上浮过程中的气团体积越大；气团体积越大，受浮力的作用越强，向上运动得越快，泄漏孔径为100 mm时气体上浮至水面仅需4.1 s。

（3）研究不同水流速度下的水下泄漏气体扩散轨迹，发现水流速度对气泡运动的水平最大运移距离起决定性作用。水流速度越大，气体受水流的推动作用越明显，气体运动轨迹与海底的夹角越小，沿海流方向的水平运移距离越大。2倍水面流速条件下扩散至海面的最右侧气体距泄漏口的水平最大距离可达22 m，扩散距离最远。

［1］ 赵冬岩，余建星.海底管道完整性管理研究［J］.海洋技术学报，2008，27（4）：71⁃74.

Zhao D Y，Yu J X.Study on submarine pipeline integrity management［J］.Ocean Technology，2008，27（4）：71⁃74.

［2］ 田辉.天然气管道泄漏爆炸动力效应研究及危险区域的划分［D］.芜湖：安徽理工大学，2012.

［3］ Trevor J M.Bubble plumes in stratified environments［J］.Journal of Fluid Mechanics，1978，85（4）：655⁃672.

［4］ Milgram J H.Mean flow in round bubble plumes［J］.Journal of Fluid Mechanics，1983，133（1）：345.

［5］ Riedl M J，Fanneløp T K.Bubble plumes and their interaction with the water surface［J］.Applied Ocean Research，2000，22（2）：119⁃128.

［6］ 景海泳，余建星，杜尊峰，等.海底管道水下气体扩散FLUENT仿真分析［J］.海洋技术，2012，31（3）：82⁃85.

Jing H Y，Yu J X，Du Z F，et al.Analysis of underwater gas diffusion from piping based on FLUENT［J］.Ocean Technology，2012，31（3）：82⁃85.

［7］ 文闯，延斌，王宪全，等.海底管线天然气泄漏过程数值模拟［J］.常州大学学报（自然科学版），2015，27（2）：72⁃77.

Wen C， Yan B，Wang X Q，et al.Numerical simulation of natural gas leakage in subsea pipelines［J］.Journal of Changzhou University（Natural Science Edition），2015，27（2）：72⁃77.

［8］ 窦梓元.水体中天然气管道泄漏扩散规律及后果分析［D］.成都：西南石油大学，2015.

［9］ 李新宏，陈国明，朱红卫，等.海底输气管道泄漏天然气扩散风险研究［J］.石油科学通报，2016，1（3）：390⁃400.

Li X H，Chen G M，Zhu H W，et al.Research into the risk of natural gas spread from submarine natural gas pipeline leakage［J］.Petroleum Science Bulletin，2016，1（3）：390⁃400.

［10］ 王少雄，李玉星，刘翠伟，等.水下输气管道泄漏扩散特性模拟研究［J］.化工学报，2020，71（4）：496⁃509.

Wang S X，Li Y X，Liu C W，et al.Numerical simulation on leakage and diffusion characteristics of underwater gas pipeline［J］.化工学报，2020，71（4）：496⁃509.

［11］ 王瑞金，张凯，王刚.Fluent技术基础与应用实例［M］.北京：清华大学出版社，2007.

［12］ 熊莉芳，林源，李世武.湍流模型及其在FLUENT软件中的应用［J］.工业加热，2007，36（4）：13⁃15.

Xiong L F，Lin Y，Li S W.turbulent model and its application to the FLUENT［J］.Industrial Heating，2007，36（4）：13⁃15.

［13］ 张健，方杰，范波芹.VOF方法理论与应用综述［J］.水利水电科技进展，2005，25（2）：67⁃70.

Zhang J，Fang J，Fan B Q.Advances in research of VOF method［J］.Advances in Science and Technology of Water Resources，2005，25（2）：67⁃70.

［14］ 韩金珂.水下输气管道泄漏扩散特性研究［D］.青岛：中国石油大学（华东），2018.

［15］ 王明强，朱永梅，刘文欣.有限元网格划分方法应用研究［J］.机械设计与制造，2004（1）：22⁃24.

Wang M Q，Zhu Y M，Liu W X.The research on finite element mesh generation method［J］.Machinery Design & Manufacture，2004（1）：22⁃24.

［16］ Sun Y，Cao X，Liang F，et al.Investigation on underwater gas leakage and dispersion behaviors based on coupled Eulerian⁃Lagrangian CFD model⁃ScienceDirect［J］.Process Safety and Environmental Protection，2020，136：268⁃279.

［17］ Zhang Y，Zhu J，Peng Y，et al.Experimental research of flow rate and diffusion behavior of nature gas leakage underwater［J］.Journal of Loss Prevention in the Process Industries，2020，65：104⁃119.

［18］ 霍春勇，董玉华，余大涛，等.长输管线气体泄漏率的计算方法研究［J］.石油学报，2004，25（1）：101⁃105.

Huo C Y，Dong Y H，Yu D T，et al.Estimation of accidental gas release flow rate in long transmission pipelines［J］.Acta Petrolei Sinica，2004，25（1）：101⁃105.

［19］ 王大庆，霍春勇，高惠临.长输管线气体泄漏率简化计算方法［J］.天然气工业，2008，28（1）：116⁃118.

Wang D Q，Huo C Y，Gao H L.Simplified method for calculation long⁃distance pipeline leakage rate［J］.Natural Gas Industry，2008，28（1）：116⁃118.

［20］ 徐兴平.海洋石油工程概论［M］.东营：中国石油大学出版社，2007.

［21］ 朱约钧.FLUENT 15.0流场分析实战指南［M］.北京：人民邮电出版社，2015.

［22］ 王彤，谷传纲，杨波，等.非定常流动计算的PISO算法［J］.水动力学研究与进展，2003，18（2）：233⁃239.

Wang T，Gu C G，Yang B，et al.PISO algorithm for unsteady flow field［J］.Chinese Journal of Hydrodynamics，2003，18（2）：233⁃239.

［23］ 李远朋，范潮海，张茹.油田集输管道体系区域风险评价方法［J］.东北石油大学学报，2019，43（6）：118⁃124.

Li Y P，Fan C H，Zhang R，et al.Systematic regional risk assessment method for oil field gathering and transportation pipeline［J］.Journal of Northeast Petroleum University，2019，43（6）：118⁃124.

［24］ 何国玺，梁永图，李岩松，等.埋地液烃管道泄漏扩散及泄漏量测算研究进展［J］.油气储运，2017，36（1）：8⁃20.

He G X，Liang Y T，Li Y S，et al.Research progress of leakage diffusion and leakage volume calculation for buried liquid hydrocarbon pipeline［J］.Oil & Gas Storage and Transportation，2017，36（1）：8⁃20.

Simulation Study of Leakage and Diffusion of Shallow Subsea Natural Gas Pipeline

Li Yanhao1,2， Hou Lei1,2， Yu Qiaoyan1,2， Chai Chong1,2， Xiao Kaixi1,2

（1. College of Mechanical and Transportation Engineering， China University of Petroleum（Beijing），Beijing 102249，China；2. National Engineering Laboratory for Pipeline Safety， China University of Petroleum（Beijing），Beijing 102249，China）

To evaluate the consequences of leakage accidents of the shallow subsea natural gas pipeline, this paper builds a calculation model of the shallow subsea pipeline leakage and diffusion process in light of computational fluid dynamics and multiphase flow theories for the strait⁃crossing section of a natural gas pipeline abroad. Three main factors, leakage aperture, leakage rate, and water flow velocity, are selected as condition variables to simulate the motion process of the gas⁃liquid two⁃phase flow under different conditions. The results show that underwater gas diffusion can be divided into three stages: the formation of gas masses above the leakage hole, the mushroom⁃like rise of gas masses, and the splitting of gas masses from large bubbles into small ones. Leakage aperture and leakage rate have a significant effect on the time when the underwater gas diffuses to the water surface. A larger leakage aperture and a higher leakage rate lead to a larger gas leakage amount, which further results in larger volumes of underwater air masses and ultimately a shorter time for them to reach the water surface. Water flow velocity has a significant effect on gas diffusion trajectory. As water flow velocity increases, the angle between the gas trajectory and the seabed decreases, and the diffusion distance along the ocean current direction becomes longer. This study can provide scientific guidance for emergency treatment of underwater natural gas pipeline leakage accidents.

Submarine pipeline； Gas leakage； Multiphase flow； Computational fluid dynamics

TE88

A

10.3969/j.issn.1006⁃396X.2022.02.012

1006⁃396X（2022）02⁃0074⁃07

2021⁃03⁃08

2021⁃09⁃18

中国石油天然气集团有限公司——中国石油大学(北京)战略合作科技专项（ZLZX2020⁃05）。

李延豪（1996⁃），男，硕士研究生，从事管道完整性技术方面研究；E⁃mail：cup_lyh@163.com。

侯磊（1966⁃），男，博士，教授，博士生导师，从事油气管道输送技术方面研究；E⁃mail:houleicup@126.com。

（编辑 王戬丽）