基于分层全域扫描的双目相机联合标定方法
赵章焰 秦建杰 鲁恩顺
武汉理工大学 武汉 430063
0 引言
摄影测量技术是一种利用摄影设备所摄取的影像信息来测定物体在现实三维空间中的位置、形状、尺寸等信息的视觉测量技术。作为一种典型的非接触式被动测量技术,摄影测量因其信息密度高、处理智能化、场景适应性强、测量精度高等诸多优点,已经被广泛地应用在各个工程领域。
在摄影测量技术的实现过程中,摄影相机的标定是整个测量流程的基础,标定结果的准确与否将直接影响最终求解结果的对错与精度。相机的标定就是确定二维图像中像素点的位置与三维场景中点的位置的对应关系[1]。目前,应用最成熟和最广泛的传统相机标定方法有Tsai两步法、张正友标定法、三维检校场标定等,均是利用位置或结构已知的高精度标定物,通过若干像点与物点的严格映射关系来确定相机的内外参数[2]。传统相机标定方法的优点是精度高,且适用于各种类型的摄影设备,但是它对标定物的要求比较苛刻,在一些复杂测量场景中如港口机械作业现场、大型施工现场等可能无法满足。
针对传统相机标定方法过度依赖现场标定物而不能适应港口大型起重机械测量的问题,邝湘宁等[3]提出了一种基于相机标定参数刚性转换思想的双站式无控制点摄影测量方法。在该方法中,将整个测量系统分为前后2个部分,即前站和后站。前站2台相机作为测量相机,用于对起重机的实际测量,且每台前方相机均与一个刚性辅助支架固连,该辅助支架上布置有若干明显的特征点,这些特征点与相机外参形成稳定的空间几何关系;后站2台相机位置相对固定,构成一个稳定双目立体视觉系统;后方相机在室内经过标定后,可以在实际测量现场通过直接测量前方相机支架上的特征点,对前方相机的参数进行快速标定。该方法虽然克服了测量现场标定物不足的问题,但是它对后方相机标定结果的精度有极高的要求。当后方相机的参数有较大误差时,它对前方相机的参数标定必将产生巨大影响,又因为存在误差传递与放大效应,致使前方相机最终测量结果的误差进一步扩大而不能很好满足测量需求。为解决这一问题,本文在该方法基础上,提出一种固联双目相机高精度快速联合标定方法。
1 相机的标定
1.1 相机标定原理
摄影测量技术的核心思想是利用二维平面信息来还原三维空间信息,即通过相片上的像点坐标来计算其在三维世界中的物点坐标。在像点与物点的转化过程中,涉及到4个坐标系统,见图1。
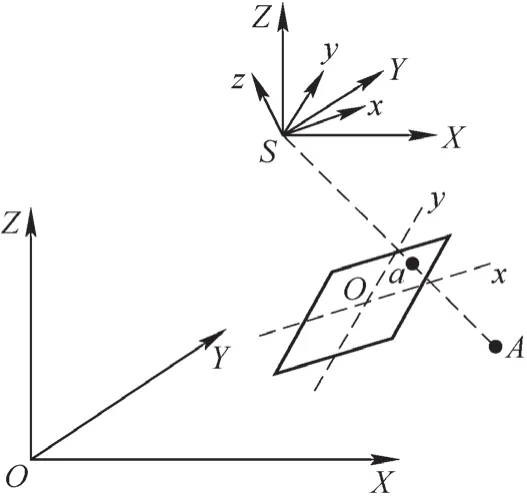
图1 4种坐标系相对关系示意图
1)像平面坐标系 也称为像主点坐标系,一般指以相片的物理中心o为坐标系原点,像素水平方向为x轴,像素垂直方向为y轴,所形成的坐标系,记为o-xy坐标系。
2)像空间坐标系 该坐标系以摄影中心S(相机的主光源)为原点,x轴和y轴分别平行于像平面坐标系的x轴和y轴,z轴为摄影方向(相机的主光轴方向),记为S-xyz。
3)像空间辅助坐标系 以摄影中心S为坐标系原点,其余各轴与物方坐标系各轴平行,记为S-XYZ。
4)物方坐标系 被测物体所在空间所确定的坐标系,可根据实际测量需求确定原点位置与各轴方向,记为O-XYZ。
在一个相片成像系统中,若二维像点a在像平面坐标系o-xyz中的坐标为(x,y),则其在像空间坐标系S-xyz中的坐标为(x-x0,y-y0,-f),其中f为相机主距,(xo,yo)为摄影中心S在像平面坐标系的投影坐标(理想状况下xo、yo均为0);若设像点在像空间辅助坐标系S-XYZ中的坐标为(X1,Y1,Z1),则二者满足

式中:R为像空间坐标系S-xyz与像空间辅助坐标系S-XYZ之间的旋转矩阵,设x轴、y轴及z轴旋转的角度分别为ω、φ、κ,则R可以表示为

像点a所表示的物点A在物方坐标系O-XYZ中的坐标为(X,Y,Z),摄影中心S的坐标为(Xs,Ys,Zs),则由摄影测量基础原理可以得到

联立式(4)得到
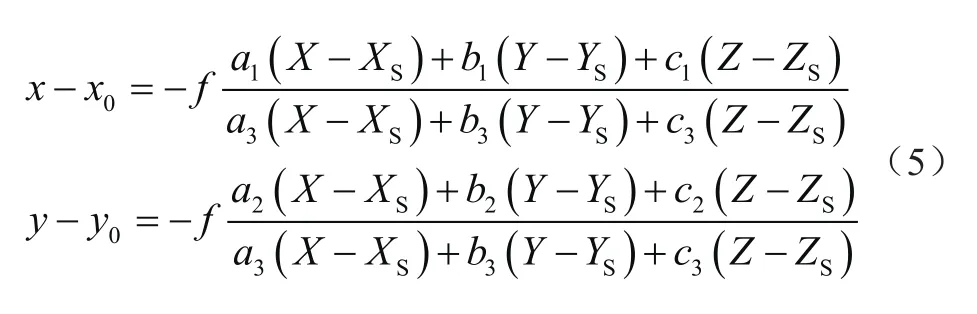
可以看出,想要实现从像点a(x,y)向物点A(X,Y,Z)的转换,需要知道 (xo,yo,f)、(Xs,Ys,Zs,φ,ω、κ)2组参数,将其分别称为摄影测量的内方位元素和外方位元素。内方位元素是描述摄影中心与相片的相互位置关系的参数,外方位元素是描述摄影中心在物方空间中的位置和姿态的参数。通过内外方位元素,可以实现4个坐标系之间的坐标转换,从而实现摄影测量的最终目标。
2 双目相机联合标定
2.1 双目相机标定误差
利用传统单目独立标定的方法存在测量误差和方程求解优化2个问题。
1)测量误差问题 三维校验场中设置的控制点坐标是用全站仪等测量工具测出的测量值,与实际值之间不可避免地存在误差;其次,在左右2张相片上点选同名点时也无法确保其像素坐标位置绝对准确。
2)方程求解优化问题 将带有误差的初始数值代入求解方程,经过严密的数学迭代计算,其最终结果是1个带有误差的理论最优解,该最优解仅在此求解体系下才是最优解,当2台相机中的任意一台改变位置再进行拍摄时,会影响到未改变位置的相机的求解结果。
2.2 基于全域扫描的双机联合标定算法
利用传统摄影测量方法采用的牛顿-拉夫逊(Newton-Raphson Method)迭代算法对单目相机的主距进行迭代求解时,由于扫描部分仅存在于线性区间,总的迭代步数不会超过相机主距搜索范围的总迭代步数,即使存在非收敛结果,依旧可以通过设置迭代时长来进行控制,所以,基于有限次迭代的全域扫描方法是标定相机的一种有效方法[4]。但是,对于双目相机系统,迭代总步数会以排列组合的形式出现巨量增长,严重影响求解速度,且测量结果解算精度对主距变化敏感,双目相机测量系统主距与解算误差关系如图2所示,故无法通过增大步距的方式来下调步数。
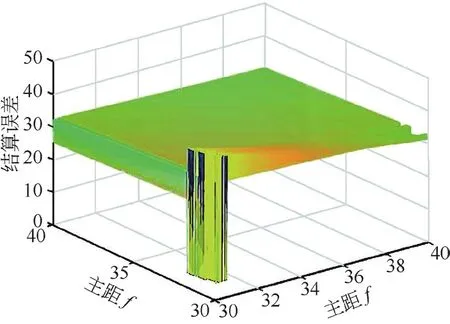
图2 双目系统关系示意图
分析图2所示的f-Δ关系图,若分别在垂直于主距fl、fr坐标平面和平行于主距fl、fr坐标平面进行切片观察,可以发现均存在唯一f使得Δ存在最小值,且该最小值与极小值重合。根据这一特性,本文提出基于全域扫描方法的双目相机联合标定算法。在该算法计算过程,每次仅对一台相机的主距区间进行扫描;将对每个主距的扫描分为内层扫描和外层扫描,内、外层主距的扫描过程中,均以另一层上次扫描的最优值作为初始参数带入求解;每次扫描标定后,进行综合误差评估,并对标定的主距做补偿调整,直到结果满足设定的误差阈值要求。该方法有效解决了传统迭代方法搜索效率低的问题,使得每次迭代都有明确的极值,有效缩短了搜索时间,提升了搜索效率,且避免了迭代步数耗尽造成的跳步问题,降低了遗漏最佳主距组合的概率。
3 实验与分析
为了验证本文所述相机标定方法的准确性和可靠性,在实验室内搭建一套双目摄影测量系统来进行标定实验。实验中所需器材包括2台相机、1台全站仪和1个简易三维检校场。2台相机分别被固定在1个稳定支架的两端,未锁紧状态下可以自由移动和旋转,调整位置和姿态来进行拍摄;当确定相机位置后将其锁紧,保证2台相机的相对位置保持不变。简易三维检校场由紧贴在墙壁上的特制标定板组成,每个标定板的中心都可以作为一个控制点;控制点坐标由全站仪测得,作为测量真值。双目相机系统和三维检校场如图3所示。实验过程共分为3步:第1步是双目相机的参数标定;第2步是对目标进行测量;第3步是实验结果与分析。

图3 双目相机和三维检校场
3.1 双目相机标定
本实验将采用传统单目独立标定和本文所述的双目联合标定2种方法,以便于进行结果对比。三维检校场中设置的控制点如图4所示,其中序号1~6的点作为相机标定控制点,用于相机的参数标定,序号a~e的点作为实验目标测量点,验证测量结果精度。双目相机到目标测量点的距离与实际测量过程中前后双站的距离相等,以真实模拟实际测量过程。由全站仪测得的各点物方坐标值如表1。

图4 相机标定控制点
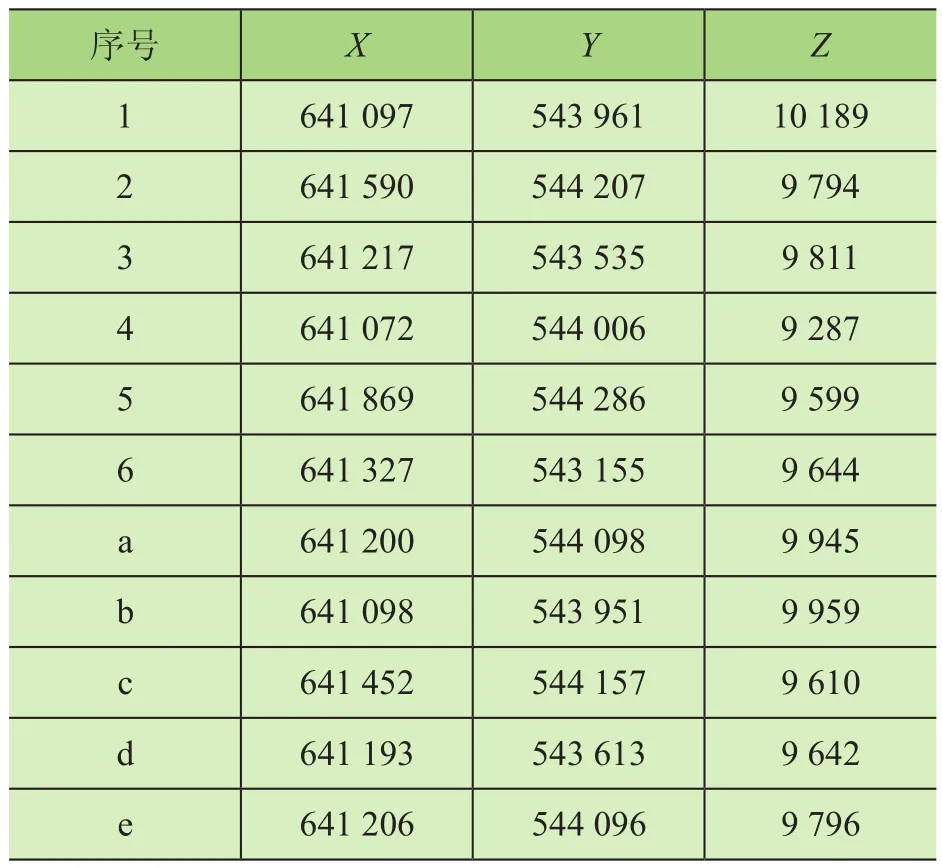
表1 检校场控制点坐标值 mm
将双目相机系统按照实验要求置于检校场内,调整相机拍摄参数及位置,拍摄若干组图像清晰的相片,然后分别用传统方法和本文方法进行相机参数标定,标定结果如表2所示。
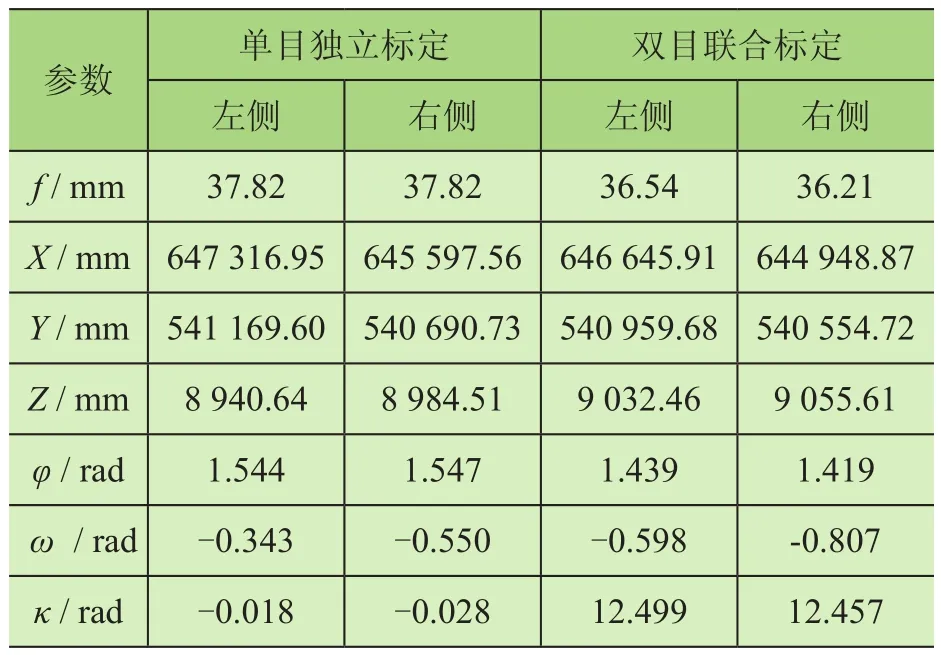
表2 相机参数标定结果
3.2 实验目标测量
完成双目相机标定后,利用所得相机参数,分别用传统方法和本文方法对实验目标测量点进行坐标测量解算,所得结果如表3、表4所示。
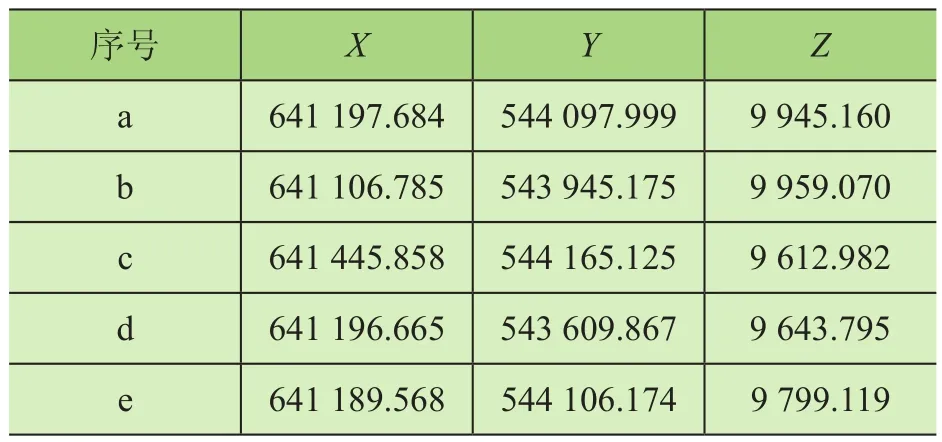
表3 传统单目独立标定相机的测量结果 mm
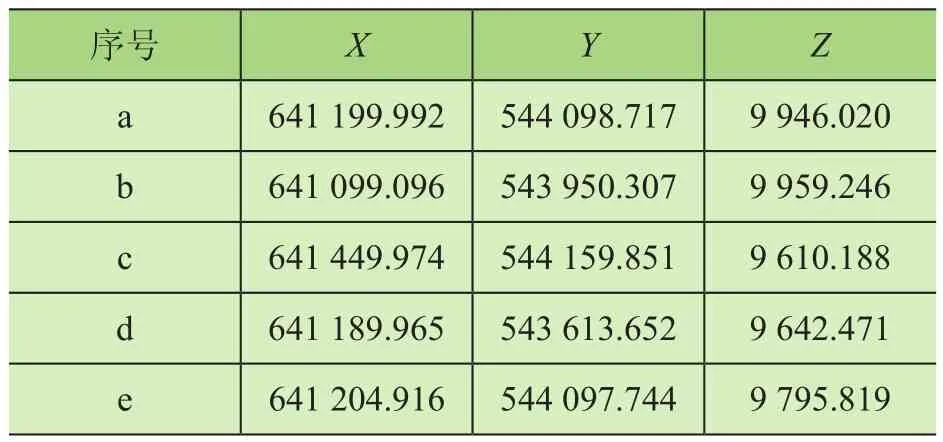
表4 双目联合标定相机的测量结果 mm
3.3 实验结果与分析
在完成目标点的测量后,对测量结果进行对比与分析。考虑到摄影测量的最终需求是获取相关尺寸数据,即点与点之间的距离,故将所测得的5个点之中任意2点之间的距离作为一组尺寸数据,来对实验结果的精度进行分析。实验结果分析如图5所示。

图5 结果对比与误差分析
在10组数据的对比分析中,使用传统单目独立标定方法的测量结果最大绝对误差为12.97 mm,最大相对误差为2.56%,平均相对误差为1.23%;采用本文提出的双目联合标定方法的测量结果最大绝对误差为2.43 mm,最大相对误差0.77%,平均相对误差为0.28%。从实验的测量结果可以看出,本文提出的双目联合标定方法具有更高的精度与稳定性。
4 结语
针对摄影测量技术中传统双目相机标定精度较低的问题,本文基于分层全域扫描方法所提出一种双目联合相机标定方法。实验数据表明,该方法在标定精度、结果稳定性、便捷性等方面较于传统方法均有明显提升,从而保证了双目摄影测量方法结果的准确性和可靠性。通过本文所述方法,可以有效改善摄影测量技术在港口起重机械上应用难的问题,使得摄影测量技术可以更好地在港口起重机的尺寸测量和运行监测等方面发挥重要作用。

