高低齿汽封表面换热系数计算方法研究
徐佳敏,李汪繁
(上海发电设备成套设计研究院有限责任公司,上海 200240)
在汽轮机转子温度场及应力场计算分析中,转子轮缘、汽封、光轴部位等表面均采用第三类边界条件,换热系数是重要参数之一[1-2]。汽封结构型式多样,主要包括高低齿、蜂窝、刷式、侧齿等,其通道结构相对复杂,且靠近转子应力集中部位。因此,转子汽封表面换热系数将在一定程度上影响转子热应力的计算精度[3],需要在转子结构安全性设计校核中予以考虑。
汽封表面换热系数主要与其自身结构参数、环境蒸汽参数相关,是空间和时间的非线性函数[4]。
20世纪80年代起,国内外学者针对汽轮机转子表面换热系数开展了不少理论分析和实验研究[5-9],主要包括实验法、解析法和经验公式法。由于实验条件、简化方法等边界不同,计算结果也存在一定差异[10-11]。目前,工程上常采用经验公式法计算换热系数。近年来,数值模拟分析技术逐步在汽封相关特性研究中应用,但主要集中在密封性能、流动特性、动力特性等方面[12-15],鲜见采用数值模拟对换热系数计算方法的研究。随着汽轮发电机组向着大容量高参数方向发展,其结构型式更加多样化。相比于采用实验研究换热系数计算方法,数值模拟方法相对更为简便快速,且适用于各种结构型式和流动状态。
本文梳理对比了汽轮机汽封表面换热系数计算的4种常用经验公式,并采用数值模拟方法针对某汽轮机高压转子轴端高低齿汽封开展了表面换热系数计算方法研究;探讨了结构参数变化对其表面换热系数的影响,结合模拟结果得到该型汽封表面换热系数的拟合公式;可为转子温度场和应力场的设计校核提供参考,同时为大容量高参数汽轮机关键部件换热系数的计算提供一种新思路。
1 经验公式方法
汽轮机转子汽封表面换热系数的计算,目前国内应用最为广泛的主要是美国西屋公司、南京工学院-哈尔滨汽轮机厂、苏联及法国阿尔斯通公司采用的经验公式[3,16-17](以下分别简称西屋公式、南工公式、苏联公式、阿尔斯通公式)。
1)西屋公式
式中:α为汽封表面换热系数,W/(m2·K);λ为蒸汽导热系数,W/(m·K);δ为汽封间隙,m;G为汽封漏汽量,kg/s;A为汽封漏汽面积,m2;η为动力黏度,Pa·s;h为汽封室高度,m;p1、p2为汽封进出口压力,Pa;υ1为汽封进口蒸汽比热容m3/kg;Z为汽封齿数。
2)南工公式
式中:S为汽封宽度,m;w为汽封间隙汽流流速,m/s;Re为雷诺数;v为运动黏度。
3)苏联公式
式中:Pr为普朗特数;C、m和n为试验常数项。 4)阿尔斯通公式
式中:p为蒸汽压力,MPa;t为蒸汽温度,℃;r0为转子外径,m;n为转速,r/min。公式适用范围为0.1 MPa<p≤2 MPa。
以某汽轮机高压转子轴端高低齿汽封为例,采用上述4种经验公式,对冷态起动过程中表面换热系数进行计算,结果如图1所示。
由图1结合计算公式可知:
1)阿尔斯通公式计算得到的换热系数明显大于另外3个公式的计算结果。究其原因,一方面是由于阿尔斯通公式中常数项相对较大,另一方面是由于该公式与蒸汽温度关联性相对较强,而在起动过程中轴端汽封部位蒸汽温度保持在较高水平。
2)西屋公式、南工公式和苏联公式的计算结果较为接近,尤其在机组起动初期。但在起动后期,由于汽封进出口蒸汽压差变大,汽封间隙汽流流速增加,雷诺数对换热系数的影响增大,致使三者计算得到的换热系数有所偏差。
此外,不同于阿尔斯通公式以部位相应的压力和温度来计算换热系数且未计入流动特性影响,西屋公式、南工公式和苏联公式在其公式结构上具有相似性,且均与汽轮机汽封结构参数(包括汽封间隙、汽封室高度、汽封齿数)密切相关,同时与蒸汽导热系数λ和雷诺数Re相关。为此,后文重点以西屋公式、南工公式和苏联公式作为对比参考开展汽封换热系数计算方法研究。
2 数值模拟计算
2.1 计算模型及网格划分
高压转子轴端高低齿汽封结构尺寸及100%负荷下蒸汽参数设定见表1。考虑到汽封结构沿周向呈周期性对称,取周向1°建立模型,并在进出口各延长5倍汽封室高度距离,以减少进出口效应对计算结果的影响,计算模型如图2所示。
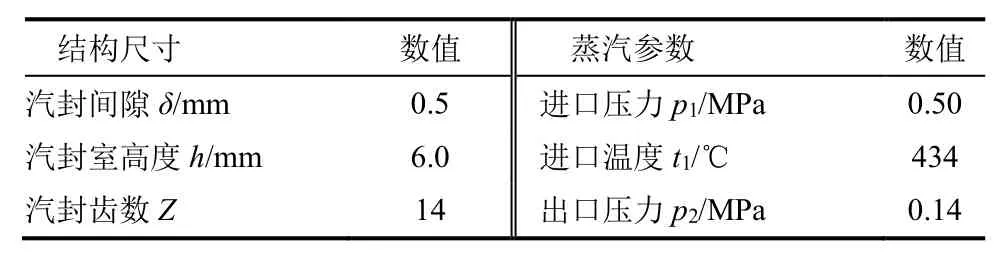
表1 汽封结构尺寸及进出口蒸汽参数设定 Tab.1 Seal structure sizes and parameters setting for steam at inlet and outlet
采用结构化网格,并对汽封靠近转子的近壁面区域网格进行加密,确保无量纲壁面距离y+<1,汽封表面y+最大值为0.195。网格间隔比设置为1.1,流动边界层内有足够数量的网格层,以确保表面换热系数计算的准确性。
2.2 数值方法及边界条件
采用计算流体力学软件,求解三维定常黏性流体雷诺时均N-S方程,湍流模型选用SST两方程模型,近壁面函数为自动壁面函数(automatic wall function)。该模型是k-ω模型的修正模型,其在主流区域采用k-ε模型,在近壁面处采用k-ω模型。在近壁面边界层内直接求解方程,保证近壁面计算精度,在流动分离、近壁面换热计算等方面优于其他湍流模型[18-20]。扩散项采用二阶中心差分格式,对流项采用高精度离散格式,残差收敛设置为10–4。
计算工质为蒸汽,进口条件为总压和总温,出口条件为静压;模型左右两侧设置为旋转周期性交接面;为了减少壁面温度对表面换热系数的影响,汽封段壁面设置为绝热计算得到的壁面平均温 度[21],其他壁面设置为光滑绝热壁面。
2.3 网格无关性及计算结果验证
以汽封漏汽量和汽封第7齿的表面换热系数为参考值,分别采用52万、69万、106万、135万、177万和217万网格节点数进行网格无关性验证。网格节点数在106万后,漏汽量和表面换热系数已基本保持不变;当网格节点数从135万增至217万时,漏气量和表面换热系数的相对变化量仅为0.01%和0.50%。为节省计算资源,网格节点数选取为135万已可满足精度要求。
为验证汽封数值计算方法和边界条件设置的正确性,采用理论公式(8)计算汽封流量系数μ,并以试验结果作为参照值进行对比[22-23]。计算得到的流量系数为0.58,与试验结果相符。同时将汽封表面换热系数与苏联公式结果相对比,误差为4.32%,验证了数值模拟边界条件设置的合理性。
式中:G为数值计算得到的汽封漏气量,kg/s;G'为理论计算得到的汽封漏气量,kg/s;ρ1为汽封进口蒸汽密度,kg/m3。
2.4 数值模拟结果及分析
为处理分析数值模拟结果,汽封表面换热系数采用公式(9)计算:
式中:h为汽封表面换热系数数值模拟结果,W/(m2·K);q为汽封表面换热量,W/m2;tw为汽封壁温,℃;tb为参考温度,即主流温度,℃。
由式(9)可知,在汽封表面换热系数数值模拟中最为关键的是参考温度选取。以往在燃机叶片内冷通道壁面、管道壁面换热等研究中,一般选取进出口平均温度作为参考温度[24-25]。但从汽封温度场分布(图3)可以看出,汽封内部温度变化较为明显,尤其是在汽封齿间隙处,蒸汽内能转化为动能致使其温度降低。若选取汽封段进出口平均温度作为参考温度,其实并不能很好地反映每个汽封齿的蒸汽主流温度。因此,本文以单个汽封齿进出口平均温度作为对应表面换热系数计算的参考温度来考虑。
汽封表面换热系数数值模拟结果如图4所示。由图4可知,除第1个汽封齿换热系数较小外,其他每个汽封齿换热系数呈周期性变化,均在汽封齿间隙出口处达到极值,且短齿出口表面换热系数较长齿出口表面大。
选取汽封段第7和第8齿进行分析,图5和 图6展示了汽封内部雷诺数、普朗特数分布和表面换热系数分布。其中,流场平面云图代表雷诺数和普朗特数,汽封壁面云图代表表面换热系数。
由图5、图6可以看出:由于汽封齿结构的影响,在汽封齿间隙进口靠近壁面处蒸汽流速较小,导致雷诺数较小,对应位置表面换热系数较小;而在汽封齿间隙出口处,由于蒸汽内能转化为动能,蒸汽流速较快,导致雷诺数较大,流动较为剧烈,对应位置表面换热系数也较大,说明汽封表面换热系数与雷诺数有很强的正相关性;普朗特数虽与换热系数也具有正相关性,但整体变化程度不大,在0.922~0.924,表征热边界层略薄于流动边界层。
3 换热系数公式拟合
3.1 汽封结构参数的影响分析
为分析不同结构参数对汽封表面换热系数的影响,在该汽轮机高压转子轴端高低齿汽封原始结构尺寸基础上,选取汽封间隙δ、汽封室高度h、汽封齿数Z3种结构参数采用单一控制变量法进行数值模拟分析。
3.1.1 汽封间隙
在汽封室高度和齿数不变的情况下,汽封间隙δ分别选取0.40、0.45、0.50、0.55、0.60 mm进行数值模拟,对应的汽封表面换热系数和雷诺数结果如图7所示。由图7可知,3种经验公式及数值模拟得到的汽封表面换热系数均随着汽封间隙增加而增大。这是由于汽封间隙与流场雷诺数计算所需的特征长度相关,雷诺数随汽封间隙增大而增加。同时,数值模拟得到的汽封表面换热系数大于经验公式计算结果。这是由于经验公式均未考虑转速的影响,计算所得流速偏小,并在常数项系数中未做相应修正,从而导致其计算得到的换热系数偏小。
3.1.2 汽封室高度
在汽封间隙和齿数不变的情况下,汽封室高度h分别选取5.0、5.5、6.0、6.5、7.0 mm进行数值模拟,对应的汽封表面换热系数和雷诺数结果如图8所示。
由图8可知,雷诺数和汽封表面换热系数均随着汽封室高度增加而降低。这是由于汽封室高度增加,汽封间隙出口流动空间变大,蒸汽动能能更加完全地转化为蒸汽热能,导致汽封间隙出口处流速降低,换热系数随之减小。也正因为如此,才导致汽封短齿出口处表面换热系数比长齿出口表面换热系数大。
3.1.3 汽封齿数
在汽封间隙和汽封室高度不变的情况下,汽封齿数Z分别选取10、12、14、16和18进行数值模拟,对应的汽封表面换热系数和雷诺数结果如图9所示。由图9可知,汽封表面换热系数均随着汽封齿数增加而降低。这是由于在汽封进口和出口蒸汽压力不变的情况下,随着汽封齿数增加,分配到每个汽封齿的压降就越小,导致汽封间隙出口处流速变小,雷诺数减小,汽封表面换热系数随之减小。
3.2 汽封表面换热系数拟合公式
从上述数值模拟和经验公式计算得到的表面换热系数可以看出,西屋公式和南工公式计算结果与数值模拟结果存在较大偏差。主要原因是两者并没有考虑普朗特数对表面换热系数的影响,且蒸汽的普朗特数不为1,因此在汽封表面换热系数的计算中需考虑普朗特数的影响。
同时,鉴于数值模拟结果与苏联公式计算结果较为接近,选取与汽封表面换热系数相关的汽封结构(汽封间隙、汽封室高度、汽封齿数)和蒸汽参数(蒸汽导热系数、雷诺数、普朗特数),汽封间隙流速采用理论计算公式[26],以公式(10)作为该高低齿汽封表面换热系数基本格式,拟合出相关系数,以期为汽封表面换热系数的计算提供参考。
当压比p2/p1>Kcr时,
当压比p2/p1≤Kcr时,
式中:Kcr为判断系数,。
公式(10)中系数a、b和c的取值是准确计算换热系数的关键。基于数值模拟得到不同结构参数下的汽封表面换热系数计算结果,将公式(10)对数处理后采用线性拟合方法,得到系数a、b和c分别是0.753 1、0.683 9和0.666 8。拟合结果与数值模拟结果最大偏差仅为1.11%,均方根偏差为0.81%,拟合相关系数R2为0.99。因此,高低齿汽封表面换热系数拟合公式为:
3.3 拟合公式在不同蒸汽参数下的适用性验证
为验证汽封表面换热系数拟合公式在汽封不同蒸汽参数下的适用性,采用设定的75%、50%负荷下汽封蒸汽参数进行数值模拟,并与苏联公式和拟合公式计算结果进行对比,结果见表2。拟合公式计算结果与数值模拟结果的偏差分别为1.05%和1.46%,说明该拟合公式适用于高低齿汽封在不同蒸汽参数下表面换热系数的计算。同时,拟合公式换热系数大于苏联公式计算结果,用于转子结构设计及安全校核计算将偏向安全。
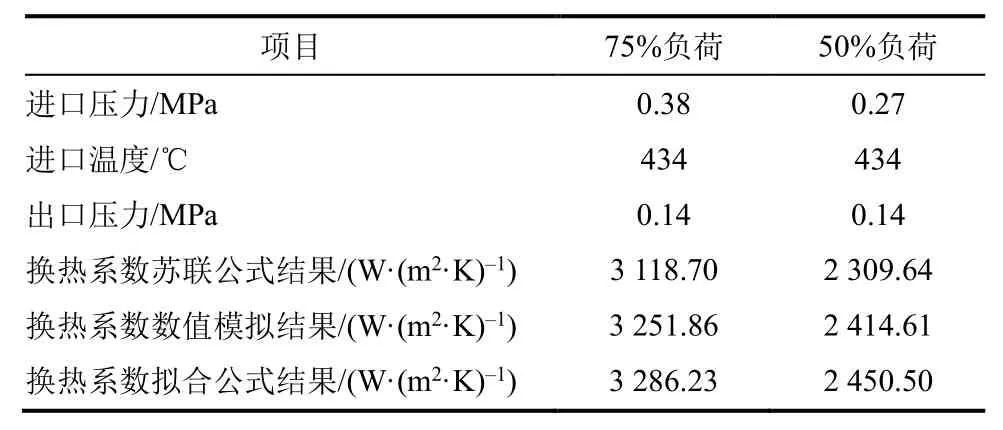
表2 不同蒸汽参数下汽封表面换热系数 Tab.2 The seal surface heat transfer coefficients at different steam parameters
4 结 论
本文对比分析了汽轮机转子汽封表面换热系数4种常用经验公式,并采用数值模拟方法研究了汽轮机高低齿汽封的表面换热系数计算方法,分析了汽封不同结构参数对其表面换热系数的影响规律,从而得到换热系数拟合公式。
1)4种常用经验公式均采取了不同程度的简化。阿尔斯通公式计算得到的汽封表面换热系数明显高于西屋公式、南工公式和苏联公式计算结果;后三者计算公式均与汽封间隙、汽封室高度、汽封齿数、蒸汽导热系数和雷诺数相关。
2)汽封表面换热系数按汽封齿呈周期性变化,在汽封齿间隙出口处出现极值,且与壁面附近流场的雷诺数和普朗特数正相关。同时,汽封表面换热系数随着汽封间隙的减小、汽封室高度或齿数的增加而减小,数值模拟与经验公式计算结果规律相一致。
3)结合数值模拟结果和经验公式,以雷诺数、普朗特数和结构参数为主要依据,得到汽封表面换热系数拟合公式。结果表明,该公式具有较好的适用性。本文方法可为大容量高参数汽轮机关键部件换热系数的计算提供一种新思路。

