长株潭城市群PM2.5多尺度演化的EEMD和多重分形分析
杜娟,刘春琼,吴波,张娇,黄毅,史凯∗
(1吉首大学数学与统计学院,湖南 吉首 416000;2洪江高新技术产业开发区(洪江市)管理委员会, 湖南 怀化 418000;3吉首大学生物资源与环境科学学院,湖南 吉首 416000)
0 引言
近年来,大范围、长时间、高频率的严重灰霾天气过程已成为我国大部分城市的主要环境问题,引起了不少学者的广泛关注[1−4]。PM2.5是影响空气质量的重要污染物[5],高浓度的PM2.5会对人体健康造成危害[6−8]。因此,研究PM2.5时空演化的多时间尺度特征及其主要动力机制,对制定区域空气质量管理政策和污染控制措施具有重要意义。
大气系统中PM2.5时空演化是一个高度复杂的过程,既受到物理和化学等条件的限制,也受到气象、地形、下垫面特征和人为排放等多种因素的影响。这些因素往往具有非常复杂的相互作用模式,使得PM2.5演化呈现不规则、非线性和复杂性的行为。复杂的空气污染演化在不同时间尺度上会产生一些复杂的空气污染特征,因此对大气污染多时间尺度演化规律的认识是分析大气污染复杂动力机制的关键。然而,基于传统线性分析方法难以精确表述大气污染多时间尺度的演化规律。许多研究表明,城市大气污染演化具有自相似性、长期持续性以及多重分形结构等非线性规律[9−12]。而多重分形消除趋势波动分析(MFDFA)是一种广泛用于定量描述复杂系统非线性演化的多尺度特征技术[13],有助于理解污染物演化的内在规律[14]。基于MFDFA可以得到奇异谱,并从中提取具有多重分形特征的重要信息,时间序列结构的复杂性是通过这些信息推断出来的[15]。基于多重分形法分析空气污染物的演化特征已成为大气污染环境领域的研究热点。例如,Shen等[16]应用MFDFA对南京市大气污染指数(API)进行分析,发现API均具有多重分形特征,其时间序列结构的变化主要与长程相关有关。黄毅等[17]对成都市空气污染物浓度进行研究,发现污染物浓度演化存在较强的多重分形特征,长期持续性是污染物浓度演化的主要动力机制。史凯等[12]前期对上海市的API进行分析,发现API具有尺度不变性、长程相关性和多重分形等特征,其多重分形参数可以作为评估城市空气质量的一个重要指标。因此,将多重分形方法用于研究大气污染多时间尺度的演化规律在方法学上具有重要应用价值[18]。
由于人为污染排放具有一定的规律性,城市中PM2.5浓度波动并不完全是非线性的。杜娟等[19]前期研究表明,PM2.5浓度极端波动时间序列中还包括高频项、周期项、趋势项以及随机项等模态分量。很多重污染的发生往往是一个很快速的过程,例如PM2.5浓度在短时间内呈爆发式增长。然而,基于传统线性分析方法难以获取这种短期内具有高频率特征的PM2.5演化模态。因此,有必要寻找新的方法,从大气PM2.5污染演变的时间序列中提取高频非线性模态。这样,有助于准确描述大气PM2.5在不同时间尺度上的演化特征,从而进一步认识PM2.5多尺度演化的内在规律。
集合经验模态分解(EEMD)是由Wu和Huang[20]于2009提出的一种处理非线性、非平稳时间序列的多尺度分析技术。该方法能自适应地将非平稳时间序列分解为高频项、周期项和趋势项等模态分量。其中,高频项包含短周期高频率的特征模态信息。该方法的优点是在原始序列中加入了高斯白噪声,以有效提取时间序列中嵌入的周期和趋势信息。EEMD方法还可以根据原始序列的局部特征实现分解,是分析非线性、非平稳时间序列的理想工具。鉴于这些优点,该方法在水文[21,22]和股票价格[23−25]等领域得到广泛的应用。EEMD方法可以从大气PM2.5浓度的时间序列中提取具有短周期高频率的特征模态。这样,有助于进一步分析复杂系统中大气PM2.5演化的多时间尺度特征。
长株潭城市群地处湖南省的中东部,该城市群以机械制造、交通运输装备制造、有色冶金、化工原料等高污染产业为主[26,27]。长株潭城市群呈品字形分布,株洲的地形比较特殊,处于罗霄与雪峰山脉之间,成为该城市群的气流交汇处。因此,该城市群近地层大气静稳天气频发,城市间污染物相互迭加,从而容易导致区域性污染[28],区域主要污染物是PM2.5[27]。本文将长株潭城市群PM2.5作为研究对象。首先,利用EEMD从PM2.5的时间序列中提取具有短周期高频率的特征模态。然后,采用MFDFA方法识别其特征模态随时间的变化是否存在多重分形特征,并研究PM2.5多重分形特征的演化规律,讨论其多重分形特征的动力来源,尝试用多重分形参数准确地描述重度灰霾期间PM2.5演化的动力特征。以期为PM2.5演化的主要动力机制的研究提供新途径,同时也为区域空气质量管理政策提供新的理论依据。
1 研究数据与方法
1.1 研究数据
长株潭是我国长江经济带、长江中游的主要城市群,其核心城市由湘潭、长沙和株洲三市组成。该城市群的空气污染非常严重,PM2.5已成为空气污染的主要防治对象。本研究将2015年1月1日–2019年12月31日长沙、株洲和湘潭三市的PM2.5小时质量浓度作为研究对象。通过对各监测子站的浓度数据进行求和并平均得到各城市的PM2.5小时质量浓度数据,其数据来自全国城市空气质量实时发布平台。个别缺失的数据用两个相邻数据的平均值替换,数据缺失率远低于1%。本研究所使用的气象资料来自中国气象数据网站中长株潭三个城市2015–2019年近五年的气温、降水量、风速等观测资料。
图1展示了2015–2019年长株潭三个城市的PM2.5浓度演化过程。由图可知,在五年时间尺度上,PM2.5浓度演化大致呈现冬季高夏季低的周期变化模式。此外,PM2.5浓度演化除了具有周期变化模式之外,还具有许多高频的非线性变化模态。这些高频模态非线性变化特征所对应的周期难以直观观察得出。因此,需要进一步应用EEMD分解方法对其高频模态进行提取分析。
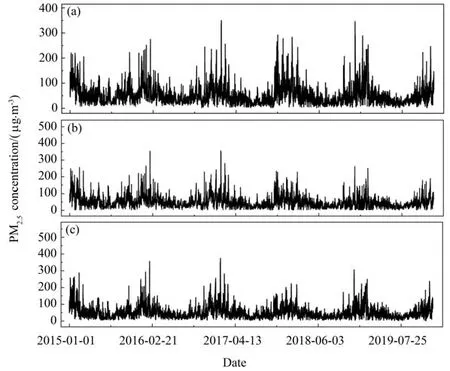
图1 2015年1月1日–2019年12月31日三个城市的PM2.5小时质量浓度数据。(a)湘潭;(b)长沙;(c)株洲Fig.1 The hourly concentrations of PM2.5from January 1st,2015 to December 31st,2019 of the three cities.(a)Xiangtan;(b)Changsha;(c)Zhuzhou
1.2 研究方法
1.2.1 集合经验模态分解法
集合经验模态分解(EEMD)能从PM2.5的原始时间序列中提取一系列具有一定物理意义的本征模态函数(IMF)[20]。EEMD既包含经验模态分解(EMD)的自适应性,还可以克服模态混叠问题。EEMD是在PM2.5的原始时间序列中加入无相关性且具有均匀尺度的高斯白噪声,使不同时间尺度上的信号变化连续,且改变其极值点的特性。还可以从PM2.5序列中提取具有独立的时间尺度分量,用于研究不同时间尺度下PM2.5演化的内在行为。每个IMF应满足两个条件[20,29],一是整组数据中,局部极值和过零点的个数需相等或最多相差1个;二是任何时间点上,上下包络线的均值需为0。EEMD具体分解步骤如下[29]:
首先,将白噪声ak(t)添加到PM2.5的原始时间序列Y(t)中,以构造一个新的序列:

式中Yk(t)为第k次添加白噪声后的信号。
其次,为消除ak(t)的影响,将N次分解的模态分量均值作为最终分量,其构造式为

式中Hj(t)指对原序列进行N次分解得的第j个分量,表示第k次EEMD分解得到的第j个IMF分量。
然后,白噪声对信号的影响为

式中e指标准差,设为0.2;d指振幅;M指集合数,其值为100[30],M越大,PM2.5序列分解值越靠近真实值。
最后,原序列的公式为

式中各个IMF分量H1(t),H2(t),···,Hm(t)分别代表不同时间尺度上的波动分量,其周期尺度从小到大依次递增;rm(t)指残差;m指分量个数。
1.2.2 多重分形消除趋势波动分析法
MFDFA已被证明是一种测量非平稳时间序列多重分形特性的有效方法[31−34]。该方法不仅能够对分形结构的不规则和不均匀程度进行度量,还可以识别非平稳时间序列中的长期持续性,以及判别其序列是否具有多重分形特征。MFDFA具体计算步骤如下:
1)对PM2.5序列x(k)(k=1,2,···,N)的累积离差序列X(i)进行计算,其公式为

2)将整个PM2.5的X(i)分割为Ns=[N/s]个互不重叠的等长区间。由于N可能不是s的整数倍,为了不遗漏末端部分,将X(i)序列从反向重复上述分割。从而得到2Ns个区间,包含了该序列的所有数据。
3)将每个子区间v(v=1,2,···,2Ns)用最小二乘法拟合,计算2Ns个子区间的趋势序列得到各子区间序列的平方均值为

4)整个序列的q阶波动函数的计算公式为
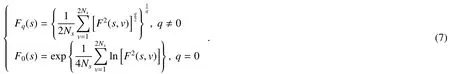
若q分别取某数值,尺度s取值不同时,则通过分析Fq(s)与s的对数图,得到波动函数Fq(s)与尺度s之间存在幂率关系,即

式中h(q)为广义的Hurst指数。当q=2时,表明PM2.5序列是单一分形。当h(q)随q的变化保持一个常数不变时,表明研究序列演化呈现单分形结构;当h(q)是q的非线性函数时,则序列的局部结构存在多重分形特征。当h(q)>0.5时,表明PM2.5序列的小幅波动与大幅波动存在较强的长期持续性特征;当h(q)<0.5时,表明其具有反持续性;当h(q)=0.5时,PM2.5序列的波动表现出无规律性。
5)PM2.5序列的复杂性程度可以通过∆h来衡量,如

∆h越大,则表明PM2.5浓度序列演化过程中存在的多重分形特征越强。
2 结果分析
2.1 PM2.5时空演化的EEMD分解
为提取具有短周期高频率的特征模态,采用EEMD方法对各城市PM2.5的原始时间序列进行分解,分解结果如图2所示。通过EEMD方法均可以将长株潭三个城市PM2.5的原始时间序列分解为14个IMF分量和1个长期趋势项(RES)。其中,长期趋势项可以反映各城市PM2.5浓度序列在近五年的总体变化趋势。长株潭三个城市的长期趋势项均呈现逐渐下降的趋势,表示研究时段内各城市PM2.5浓度在逐渐下降。其中,株洲的长期趋势项的下降速率最快,其次是湘潭和长沙,说明长株潭城市群实施的大气污染行动计划对空气污染的治理有显著成效。这也是近年来开展相关环保工作带来的成效。每个城市的各IMF分量均展示了PM2.5演化模态在不同时间尺度上从最高频率到最低频率的波动特征。随着频率由高到低的变化,每个IMF的振幅变得越来越大。各IMF分量的信号波动均具有各自的准周期。在同一研究时间段内,不同时间尺度上的分量浓度振荡呈不同强度的非均匀变化,表明空气污染系统内外力共同作用具有非线性特征。因此需要计算各IMF的平均周期。

图2 PM2.5浓度时间序列的EEMD分解结果。(a)湘潭;(b)长沙;(c)株洲Fig.2 EEMD decomposition results of PM2.5concentration time series for the three cities.(a)Xiangtan;(b)Changsha;(c)Zhuzhou
各IMF分量的信号波动对原序列的影响可以采用方差贡献率来反映,因此需要计算每一个城市各IMF的平均周期和方差贡献率。通过快速傅立叶变换(FFT)计算IMF的平均周期和方差贡献率,计算结果见表1。其中,IMF的平均周期表示各IMF的点数除以峰值数所得的值,IMF的方差贡献率为各IMF对应的方差除以总IMF分量与趋势项之和所得的值。湘潭市前8个模态分别具有准3 h(IMF1)、准12 h(IMF2)、准24 h(IMF3)、准 48 h(IMF4)、准 108 h(IMF5)、准 168 h(IMF6)、准 503 h(IMF7)、准 617 h(IMF8)的振荡周期,长沙和株洲市前8个模态的准周期均在617 h以内。各城市剩余IMF分量的平均周期均大于617 h。在617 h内的前8个模态具有近似一致的周期振荡特征,其准周期的波动对应一个月以内的时间尺度。各城市前8个高频分量对PM2.5浓度总体波动的影响较大,其累积方差贡献率分别为51.60%(湘潭)、61.14%(长沙)、50.61%(株洲)。三个城市前8个高频分量的累积方差贡献率相差不大,反映出三个城市呈明显的区域污染特征。剩余的模态对PM2.5浓度总体波动的贡献相对较小。从较长的时间尺度(五年)来说,长株潭城市群主要以静稳天气为主。由于污染物长距离输送需要较长的时间,不会在很短时间内就能从远处长距离输送过来,因此短周期的高频模态不太可能是由外来输送导致。因此可以推断,外来输送不会存在稳定的短周期高频率特征模态。各城市PM2.5的高频累加模态(前8个模态之和)可以更好地反映出长株潭城市群区域大气污染排放并在大气系统中发生复杂非线性作用而导致的特征变化。
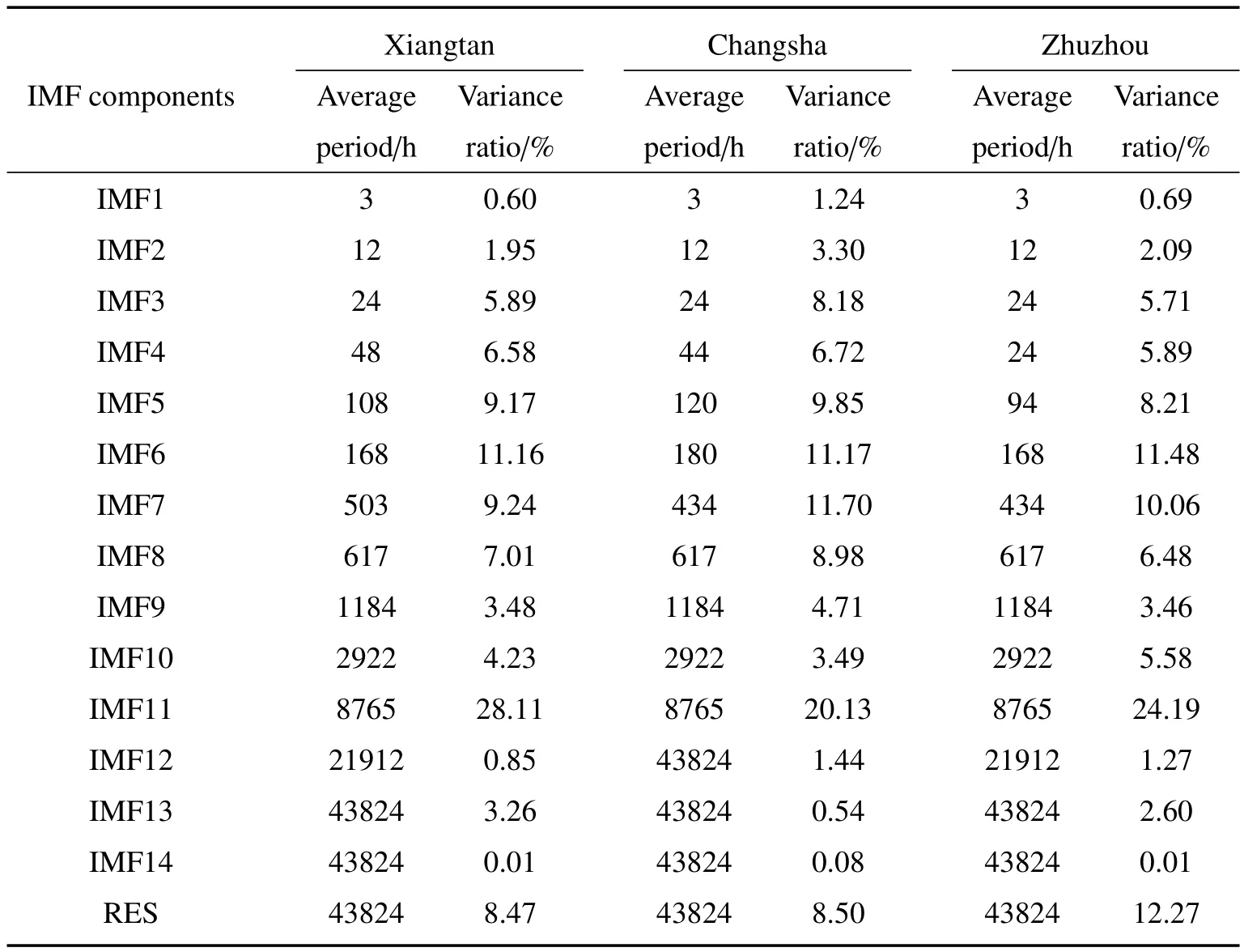
表1 三个城市各IMF分量的主要统计值Table 1 The main statistical values of IMFs of the three cities
2.2 PM2.5时空演化的多重分形特征
首先对PM2.5高频模态的演化是否具有多重分形特征进行识别。应用MFDFA方法对各城市PM2.5的高频累加模态进行计算,结果如图3所示。从图3(a)-(c)可以看到,对于各城市中的每一个序列,从q=−20到q=20的直线都能很好地拟合Fq(s)与s的波动函数曲线,表明波动函数Fq(s)与尺度s之间存在幂率关系。各城市的h(q)与q的广义Hurst指数如图3(d)-(f)所示,每一个城市PM2.5序列的h(q)均随q的增大而减小,这表明各城市PM2.5的高频累加模态存在多重分形特征。为了衡量其多重分形的强度,计算得到各城市的∆h值分别为0.79(湘潭)、0.78(长沙)及0.80(株洲),h(2)值分别为0.74(湘潭)、0.76(长沙)及0.86(株洲)。其中,h(2)均大于0.5,说明各城市PM2.5的高频累加模态演化存在较强的长期持续性特征。
一般来说,多重分形有两个主要来源[35,36]。一种是其小幅波动和大幅波动在不同时间尺度下的持续影响,另一种是其极端值的尖峰胖尾概率分布。通过洗牌过程(洗牌数据)和相位随机替换过程(替代数据)可以发现这两种动力机制的来源。洗牌过程可以破坏数据中的时间相关性,保持原始数据的分布。由于洗牌过程中打乱了多重分形的所有相关性,则该序列呈单分形,说明随机序列能识别长期持续性对多重分形有影响。为辨别尖峰胖尾概率分布对多重分形是否有影响,使用了替代数据。由于相位随机替换方法可以破坏序列中的非线性特征而保存原始时间序列的线性性质,所以替换序列能辨别尖峰胖尾概率分布对多重分形的影响。
运用MFDFA方法对各城市PM2.5的高频累加模态数据分别进行随机重构和相位随机替代,从而获得随机数据和替换数据。图3(d)-(f)展示出了不同时间尺度下洗牌数据和替换数据的h(q)值。各城市原始PM2.5的高频累加模态序列h(q)对q的依赖性均高于其洗牌序列和替换序列。各城市的洗牌序列,其h(q)对q的依赖性最低。这一现象反映出原始PM2.5多重分形行为是由长期持续性导致。同时,各城市替代数据的h(q)对q的依赖性与原始PM2.5序列的差异性较小,而随机序列却相差很大,这说明长期持续性是导致各城市PM2.5的高频累加模态随时间演化的主要动力机制。也就是说,在五年时间尺度上,PM2.5浓度的小幅波动或大幅波动在不同时间尺度内的长期持续性作用,是造成长株潭城市群PM2.5浓度波动的主要动力因素,而尖峰胖尾作用不大。
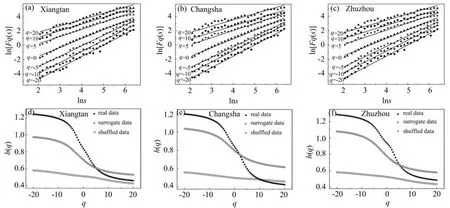
图3 三个城市PM2.5高频累加模态的波动函数Fq(s)对数图(a)-(c)和广义Hurst指数(d)-(f)Fig.3 Log-log plots of fluctuation function(a)-(c)and generalized Hurst exponents(d)-(f)of high-frequency accumulation modes of PM2.5for the three cities
2.3 气象条件对PM2.5序列多重分形强度的影响
尽管多重分形参数能较好地研究PM2.5序列的动态复杂性,但在整个研究时段内PM2.5序列的多重分形参数并不能反映出其时间序列行为的动态变化状况。为了更好地展示PM2.5序列的动态变化过程,需要在不同时间尺度上分析其多重分形的时间演变。由于PM2.5序列的复杂性程度可以用多重分形强度来度量,因此,在月时间尺度上,分别应用MFDFA方法计算各城市PM2.5的高频累加模态多重分形强度值的逐月变化规律,计算结果如图4所示。进一步,统计分析了各城市PM2.5的高频累加模态多重分形强度值的月均变化模式,结果如图5(a)-(c)所示。结果表明,各城市PM2.5序列的值在一月份达到第一个峰值,随后各月逐渐下降,在6月份达到最低值,随后逐渐增大,直到10月份或11月份达到第二个峰值。从总体来看,各城市PM2.5序列的∆h值均表现出一定的周期波动特征,整体呈现出冬季高、夏季低的变化规律。这说明其多重分形强度很可能受到气象因素的影响。进一步统计了三个城市2015–2019年气温和降水量的月均变化模式如图5(d)-(f)所示,从总体上来看,各城市6月份的降雨量最高,7月份的平均气温最高。各城市的平均气温和降水量的月均变化模式具有典型的周期变化特征。各城市PM2.5的高频累加模态多重分形强度值的波动特征与其气象要素的变化具有较强的相关性变化规律。因此,气象条件的变化对PM2.5的高频累加模态多时间尺度演化的多重分形强度会带来较大影响。
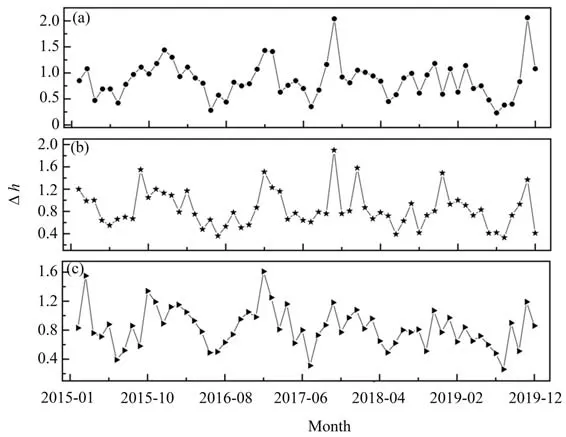
图4 PM2.5的高频累加模态∆h值在近五年时间尺度上的逐月变化趋势。(a)湘潭;(b)长沙;(c)株洲Fig.4 The monthly variability of∆h values for high-frequency accumulation modes of PM2.5.(a)Xiangtan;(b)Changsha;(c)Zhuzhou

图5 PM2.5的高频累加模态∆h值(a)-(c)和气象要素(d)-(f)在近五年时间尺度上的月均变化模式Fig.5 The monthly average variability of∆h values for high-frequency accumulation modes of PM2.5(a)-(c)and meteorological factors(d)-(f)on five-year time-scales
3 讨论
PM2.5时空演化的EEMD分析表明,长株潭三市的趋势项均反映了PM2.5浓度在近几年呈逐渐下降的趋势,说明长株潭地区实施的大气污染行动计划对空气污染的治理有显著成效。由于空气污染物浓度演化过程中具有不同的周期,各城市具有短周期的前8个高频分量的累积方差贡献率均达50%以上,表明具有短周期的高频分量对空气污染物浓度波动特征的影响较大。因此空气污染物高频累加模态的非线性波动更能反映该区域大气污染的非线性演化趋势。
PM2.5时空演化的多重分形分析表明,长株潭地区大气PM2.5的高频累加模态在不同时间尺度上的演化主要受长期持续性内禀动力机制主导控制。在长期持续性机制的作用下,PM2.5的高频累加模态在一定时间尺度内表现出较强的持续作用,这与经典的马尔可夫过程不同。PM2.5的长期持续性特征表明,该区域过去一定时间段内污染源排放的污染物会以幂律的形式持久地影响当前乃至未来PM2.5的时空演化趋势。长期持续机制反映了PM2.5浓度波动演变的内在动力因素,长株潭城市群大气系统中PM2.5浓度的演化趋势对过去较长时间尺度内PM2.5的浓度波动具有较强的敏感性和依赖性。
长株潭城市位于湖南省中东部地区,属于亚热带季风性湿润气候。长株潭城市群呈品字形分布,城市之间距离不足40 km。在研究时间尺度内,长沙、株洲和湘潭三市的年均气温分别为18.2、17.6、18.6◦C,年均风速分别为1.3、2.6、1.7 m·s−1,年均降水量分别为1351、1477、1593 mm。三市在气候上具有相似特征。以往的研究表明,气象条件(如气温、降水量等)是影响大气污染物的分布和浓度的重要因素[37−40],大气污染物的长期持续性也会受到不同时间尺度上气象条件的强烈影响[41]。其中,在夏季,长沙、株洲和湘潭三市的平均气温分别为27.4、28.3、28.1◦C,平均风速分别为2.3、1.8、1.3 m·s−1,平均降水量分别为183.9、195.8、161.8 mm。较高的地表温度会增加温度的垂直下降速率,有利于污染物的扩散。当降水量增大,空气湿度较高,有利于大气颗粒物与水汽的粘附。空气湿度一旦升高,就会形成有效降水,对大气污染物有冲刷和清除作用。气温和降水量的增加将有效降低大气污染物浓度的累积效应,使得低浓度与高浓度的PM2.5之间波动的变异性较小。这是长株潭城市群PM2.5高频累加模态的多重分形强度在夏季均较弱的原因。在冬季,长沙、株洲和湘潭三市的平均气温分别为6.9、7.8、7.5◦C,平均风速分别为2.9、1.6、1.2 m·s−1,平均降水量分别为66.7、72.1、58.8 mm。冬季以静小风为主,城市空气污染物不易水平扩散。早晚平均气温均较低,对流作用减弱,近地层大气结构相对稳定,容易出现逆温天气。进而有利于污染物累积,使得污染物不能在垂直方向稀释扩散。加上冬季降雨量较少,不利于大气污染物的清除。从而有效加强了大气污染物的累积效应,容易产生高浓度的PM2.5污染,使得低浓度与高浓度的PM2.5之间波动的变异性较强。因此,这是长株潭城市群PM2.5高频累加模态的多重分形强度在冬季均较强的原因。三市PM2.5高频累加模态的非线性演化具有相似特征,这也从一个侧面印证了长株潭大气污染具有典型的区域性污染特征[28]。
由于大气污染行动计划执行力度较大,长株潭城市群空气污染控制效果较好,使得近几年PM2.5浓度逐渐下降。然而,大气PM2.5演化过程中,其高频累加模态多重分形特征并没有随PM2.5浓度的逐渐下降而出现明显减弱的趋势。主要原因在于,长株潭PM2.5浓度的多时间尺度波动主要受长期持续动力机制的主导控制作用。特别是在冬季,污染演化的长期持续动力机制对PM2.5浓度高频模态的演化将发挥更加主导的控制作用。在该机制的作用下,过去一段时间内污染源排放PM2.5浓度的增加很可能会导致现在乃至未来一定时间段内PM2.5浓度的非线性累积。不同时间尺度上PM2.5非线性长期持续动力机制将导致冬季仍有高浓度PM2.5涌现的风险,甚至再出现更为严重的污染。
本研究提出的新EEMD-MFDFA模型可以为研究区域大气污染多时间尺度动力特征的演变提供一条新的途径。该模型可以有效地提取PM2.5的高频成分,并进一步定量揭示这些高频成分中的多重分形特征及其动力学来源。长期持续机制是使得大气污染的持续时间较长乃至未来一段时间长株潭再次出现重污染的主要动力机制,这将导致未来严重空气污染仍有可能发生。因此,长株潭地区在制定区域严重空气污染防治措施的长期规划中,应特别注意大气污染物长期持续动力机制对PM2.5多时间尺度的非线性演化特征带来的影响。
4 结论
以长株潭城市群近几年PM2.5小时质量浓度数据为基础,提出一种新的EEMD-MFDFA模型,得到的主要结论如下:
1)通过EEMD分解,分别得到湘潭、长沙和株洲前8个高频模态的平均周期、方差贡献率以及一个长期趋势项。各城市的长期趋势项均呈现出逐渐下降的趋势,反映了长株潭城市群PM2.5浓度呈现下降的趋势。各城市前8个高频模态对应的准周期与一个月时间尺度以内的周期具有近似一致的振荡特征。同时,具有短周期的前8个高频分量的累积方差贡献率均达50%以上。研究表明各城市PM2.5的高频累加模态可以更好地反映出PM2.5浓度波动的主要特征。
2)MFDFA技术证实了各城市PM2.5浓度波动演化过程均表现出多重分形行为,其高频累加模态的值分别为0.74(湘潭)、0.76(长沙)及0.86(株洲),均大于0.5,表明各城市PM2.5的高频累加模态存在较强的长期持续性特征。研究表明,PM2.5浓度小幅波动或大幅波动在不同时间尺度内的长期持续性影响是造成此次大气PM2.5污染的主要动力来源。这种长期持续性的特征反映了当前PM2.5浓度波动在一定时间尺度上受过去演化趋势的影响,这是大气污染物非线性累积效应的宏观动力学特征。
3)研究了气象条件对其高频累加模态多重分形强度的影响,研究表明各城市PM2.5高频累加模态的多重分形强度受气象条件的影响较大。在夏季,受气象条件的影响,其时间序列多重分形强度的变化是较小的,其高浓度与低浓度之间波动的变异性较小。而冬季其时间序列多重分形强度的变化趋势比较大,反映了即使是在PM2.5浓度逐年得到控制的背景下,长株潭城市群在冬季长时间尺度上仍可能出现高浓度的PM2.5污染事件。结果表明长期持续机制仍是PM2.5浓度存在多重分形特征的主要动力来源。尽管长株潭城市群采取的大气污染行动计划确实对空气污染的治理有显著成效,但在大气污染物长期持续机制的主导控制作用下,不同时间尺度上PM2.5非线性相关作用仍可能导致冬季存在高浓度PM2.5污染的风险。本研究结论有助于加强对长株潭城市群大气污染演化复杂规律的认识,对于科学制定环境保护决策具有重要意义。

