基于KL-CEEMD的风机传动系统故障诊断方法研究

韩中合，赵文波，朱霄珣，李震涛

(华北电力大学动力工程系，河北 保定 071003)

0 引 言

风力发电机传动系统故障是风电机械故障中最常见的故障之一，而其故障主要以振动形式表现，因此对该传动系统齿轮裂纹、断齿和磨损等一系列常见零部件故障振动信号进行采集分析至关重要。风机振动信号是风机传动系统故障的外在表现，通过对振动信号进行时频分析[1]，能够有效地从故障信号中提取故障信息，如广泛应用于机械故障诊断的经典小波分析[2-3]方法，然而小波分析需要经验性地选择小波基，缺乏自适应性。

除小波分析外，Huang等[4-5]提出了经验模态分解（empirical model decomposition, EMD），也是一种经典的时频分析方法，能够更加自适应地把复杂信号分解成多个有意义的分量，但是此方法还是存在模态混叠和虚假分量的缺点。Wu等进一步提出了集合平均经验模态分解（ensemble empirical model decomposition , EEMD）分解，此方法采用噪声辅助的EMD方法，可以抑制一部分模态混叠的现象，但是也存在残余噪声导致的重构误差。周颖涛等[6-7]提出EEMD改进方法，该方法改进停止准则，提高了EEMD结果的准确性，但存在模态混叠和能量削弱等问题。而胡君林等[8]提出基于希尔伯特振动分解( Hil-bert vibration decomposition, HVD)的改进方法，也存在求解复杂信号时结果精确低、计算时间长等不足。这些方法都会导致在风机传动系统振动故障信号提取中出现精确度不高的问题。

Yeh等[9]在EEMD的基础上提出了新的改进算法——互补集合平均经验模态分解（complementary ensemble empirical model decomposition，CEEMD）方法，有效地解决了EEMD分解可能造成的幅值改变问题。CEEMD有效控制了模态混叠，但虚假分量仍然极大地限制了该方法的应用。

本文针对CEEMD在风机传动系统故障诊断中出现的虚假分量问题，提出了基于KL散度的CEEMD虚假分量识别方法KL-CEEMD，利用KL散度衡量各分量和原信号的相关性大小，并与利用聚类分析寻找到的阈值进行对比，自动识别出原信号的虚假分量。此方法在分析风机传动系统的齿轮裂纹、断齿等故障信号中取得了很好的效果。

1 互补集合平均经验模态分解法

1.1 CEEMD基本原理

CEEMD是在EMD和EEMD的基础上，对其在信号分解过程中存在的模态混叠问题进行改进的方法。EMD方法相较于傅里叶变换，对于非平稳信号和非线性信号的处理上灵敏度更好，但是EMD在有冲击信号出现时，会出现模态混叠的问题[10]。模态混叠是一种原信号同一分量IMF中存在不同频率成分或者相同的频率在原信号不同分量中出现。导致模态混点的情况有多种，例如原信号中存在不稳定的高频信号、噪声的干扰、频率接近的成分等。由于EMD在信号分解中存在不足，提出了EEMD信号分解法，通过添加白噪声抑制模态混叠现象，在实际应用中具有一定效果。但EEMD在添加白噪声时，同时会使原信号的幅值和能量改变。

此后CEEMD信号分解法被提出，此方法在信号特征提取上有很好的适用性。CEEMD的主要特点是添加多对符号相反的白噪声，之后进行EMD分解，最后对分解结果集成平均得到最终的分解结果。主要步骤如下：

在原信号中添加一对噪声信号，加入的白噪声幅值相同，即

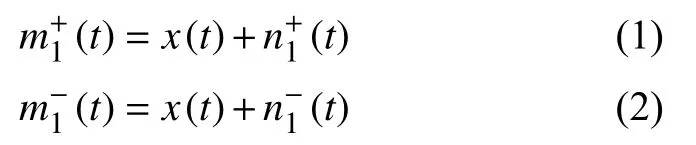
最终分解结果为

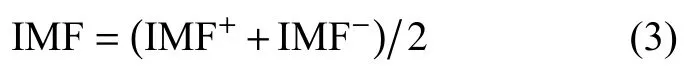
1.2 风机传动系统信号分析

在风机传动系统故障中，平行轴齿轮裂纹、断齿、缺齿和磨损的故障情况较为普遍。本文以这4种故障类型作为研究对象，通过搭建风机传动系统实验台模拟平行轴齿轮Z6的4种故障情况，其中裂纹为齿轮单齿齿根处单条裂纹，断齿为齿轮单齿断掉半齿，缺齿为齿轮单齿从根部整个缺失，磨损为齿轮单齿齿根处明显磨损，然后对其故障信号进行特征提取。本节选取齿轮裂纹和断齿故障的振动信号，利用CEEMD进行分解分析，同时将传动系统正常运行状态下的振动信号进行分解，对比分析正常信号与两种故障信号之间的异同。

利用本实验室中的风机传动系统实验台，模拟裂纹和断齿两种故障，转速为1 200 r/min，采样频率为2 000 Hz，采样点数为5 000。图1和图2为风机传动系统实验台及其传动系统图。

图1 风机传动系统仿真实验台

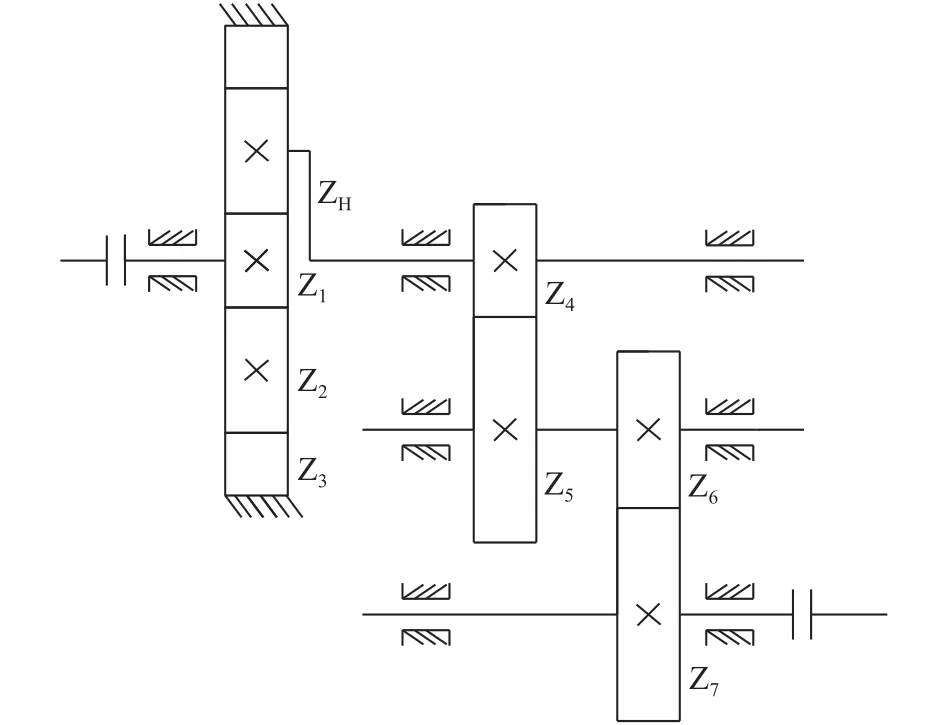
图2 风机传动系统

传动系统中的各齿轮参数如表1所示。

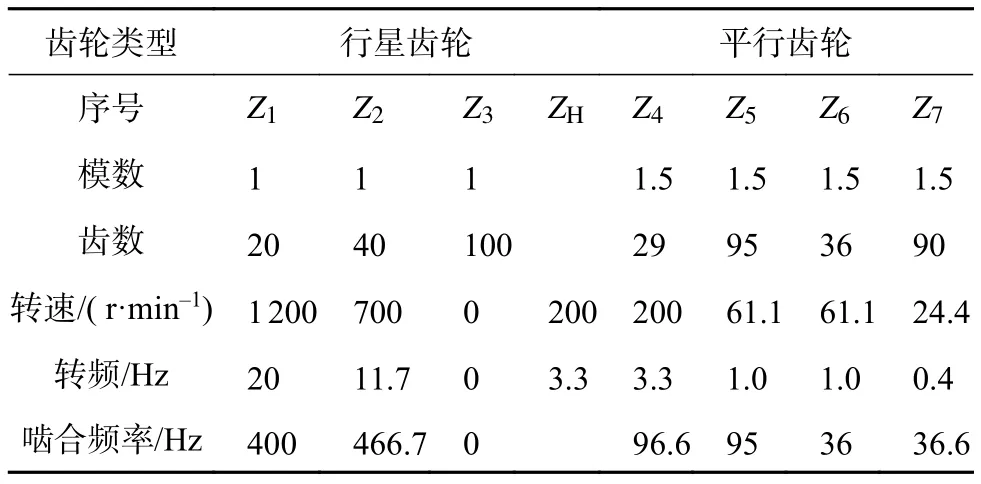
表1 齿轮相关参数

图3为风机传动系统实验台正常振动信号和两种故障振动信号的频谱图。

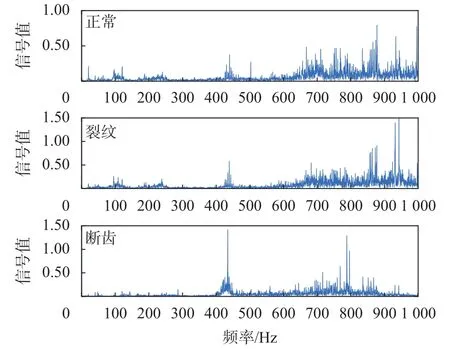
图3 三种状态振动信号频域图

在正常运转状态的频域图中能清楚地看出两个明显峰值：100 Hz和440 Hz及其倍频。与表1中的信息对比可知，两个突出的频率峰值与平行轴齿轮的啮合频率95 Hz和96.6 Hz及电动机的输出频率及行星轮啮合频率400 Hz和466.6 Hz相近，但是频谱图中还存在某些与故障有关的突出峰值，这是因为风机传动系统内部结构较复杂，频率图中有多处突出峰值是在所难免的。

通过对比两种故障状态和正常状态下的频谱图，在断齿故障频谱图中440 Hz处振动频率更突出，在裂纹故障频率图中940 Hz处振动频率更加突出。总的来说，对原始振动信号直接进行时频分析，频谱中包含的成分复杂，某个故障频率不明显，几乎很难直接分辨出，因此，在风机传动系统故障诊断识别过程中很难提取故障特征。

2 基于KL散度的CEEMD虚假分量识别方法

2.1 KL散度

KL散度[11-12]，又被称为交叉熵、相对熵等，在信息论中衡量两个概率密度分布函数的相近程度。两个分布函数的K-L值越小，其差异化越小；值越大，差异化越大。设两个离散的概率分布函数为p(x)和q(x)，则p和q的散度值为：

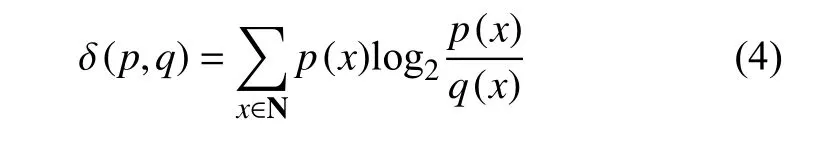
KL散度有非对称性的特点，看似δ(p,q)可以反映两个分布函数的距离，但事实上其不满足距离是对称的概念，又因KL散度由吉布斯不等式可证明其具有非负性的特点，本文为满足KL散度以上两个特点，p(x)和q(x)的散度值定义为：

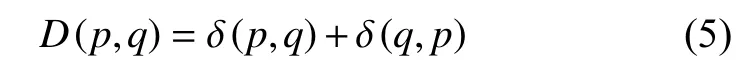
当知道两个振动信号的概率分布X=(x1,x2,x3,···,xn)和Y=(y1,y2,y3,···,yn)，且两个信号的概率密度分布函数分别为p(x)和q(x)，利用核密度估计法[13-14]，求振动信号的概率密度分布，函数公式为：

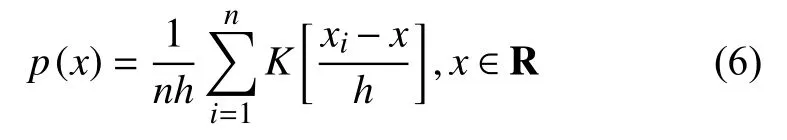
式中：p(x)——振动信号的核密度估计后的概率密度函数；

h——平滑参数；

K(·)——核函数。

上述方法普遍利用高斯核函数为K(·)，即：

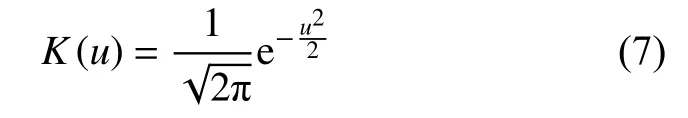
同理可得振动信号Y的概率密度分布为q(x)，然后把p(x)和q(x)带入式(4)得到 δ(p,q)和 δ(q,p)，最后带入式(5)可得D(p,q)的KL散度值。

本文通过对风机传动系统振动信号进行CEEMD分解，然后对比分析各分量和原信号，确定了虚假分量信号和原信号的概率密度分布相差更大，KL散度值也越大；反知真实分量信号和原信号的概率密度分布相差较小，KL散度值也越小。因此，本文通过给定合适的阈值[15]准确识别虚假分量并予以剔除。具体仿真信号虚假分量识别步骤如下：

1）通过CEEMD对振动信号进行分解，获取各分量IMF。

2）分析每个分量与原故障信号的KL散度值，经标准化处理后，再对获得的一系列散度值Ti进行聚类分析。

3）真假分量的KL散度值相差较大，通过聚类分析算法设定合理的阈值r，可自动识别故障信号分解后的真假分量，并将虚假分量予以剔除。

在区分虚假分量设定阈值方面，目前以设置固定值为主，在特定的故障信号虚假分量识别中有一定作用。也有学者在设定阈值方面引入了聚类的方法[16-17]，常用的方法有k-means聚类算法、DBSCAN聚类算法和高斯混合聚类法（GMM）等。

由于高斯混合聚类法能够拟合出任意形状的数据分布，而且在模型迭代计算过程中速度快，聚类表现优秀，故本文选择了高斯混合的聚类方法对虚假分量和真实分量进行自动分类，起到设定阈值的作用。此方法在故障信号虚假分量识别方面更加灵活，避免了固定阈值在不同种类故障信号虚假分量识别中的误诊现象，因此更具有普遍适用性。

2.2 KL-CEEMD方法研究

基于风机传动系统故障信号CEEMD分解过程中出现虚假分量的情况，本文提出了一种通过聚类分析的KL-CEEMD虚假分量识别剔除的方法。该方法能够对真实信号和虚假信号进行自动分类，并将原振动信号中的虚假分量剔除，流程如图4所示。

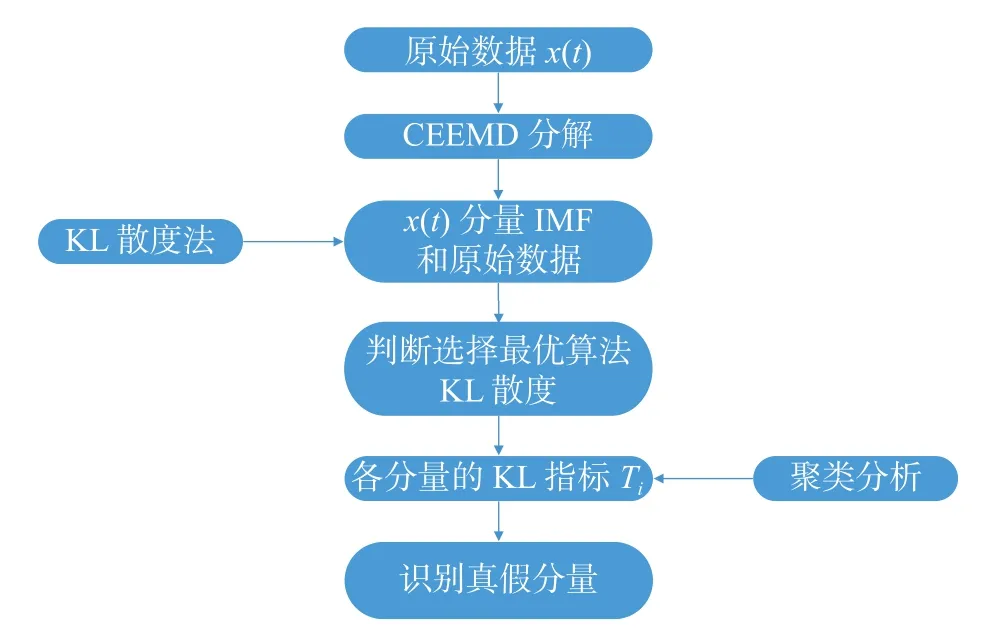
图4 KL-CEEMD虚假分量识别流程图

3 KL-CEEMD实验研究

3.1 仿真信号研究

风机传动系统结构较为复杂，其振动信号包含了正常运行以及噪声等相关信号，本节将对风机传动系统运行振动信号进行仿真，构造3个添加信噪比为40 dB噪声信号的仿真信号。

模拟仿真信号1如下：

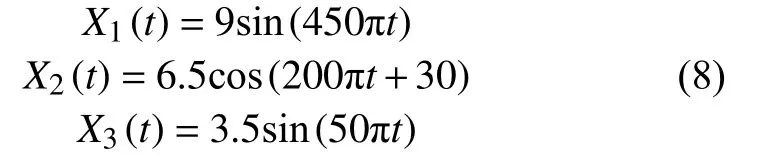
则仿真混合信号为：

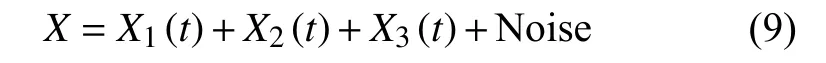
其中X1、X2和X3均为模拟风机传动系统的正常运转振动信号；假设采样频率1 000 Hz，采样点数为2 000，时间序列为t=(1∶2 000)/1 000。

由仿真信号1可知，X1的振幅为9 V，频率为225 Hz；X2的振幅为 6.5 V，频率为 100 Hz；X3的振幅为3.5 Hz，频率为25 Hz。

模拟仿真信号2如下：

则仿真混合信号为：

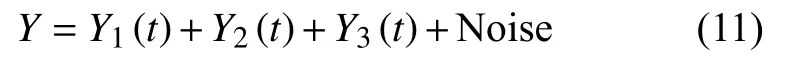
其中Y1和Y2为模拟风机传动系统的正常运转振动信号，Y3为模拟某种故障下的特征振动信号；假设采样频率1 000 Hz，采样点数为2 000，时间序列为t=(1∶2 000)/1 000。

由仿真信号2可知，Y1的振幅为3 V，频率为200 Hz；Y2的振幅为 2 V，频率为 25 Hz；Y3为正余弦两个信号相乘的调幅信号。

模拟仿真信号3如下：

则仿真混合信号为：

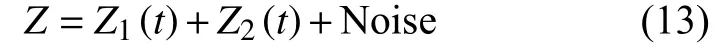
其中Z1为模拟风机传动系统的正常运转振动信号，Z2为模拟某种故障下的冲击振动信号；假设采样频率 1 000 Hz，采样点数为 2 000，时间序列为t=(1∶2 000)/1 000。

由仿真信号3可知，Z1的振幅为6 V，频率为250 Hz；Z2为初始幅值12，阻尼因子为5的衰减振荡周期信号。

采用KL-CEEMD对仿真信号进行特征提取，首先对信号进行CEEMD分解，分解结果如图5所示，分别计算分解后各分量与原混合信号的KL散度值和相关系数，同时对KL散度值进行z-score标准化处理，然后对两种评价指标进行对比分析，来说明KL散度法的优越性。最后利用高斯混合聚类模型对KL散度指标值进行聚类，结果如表2所示。

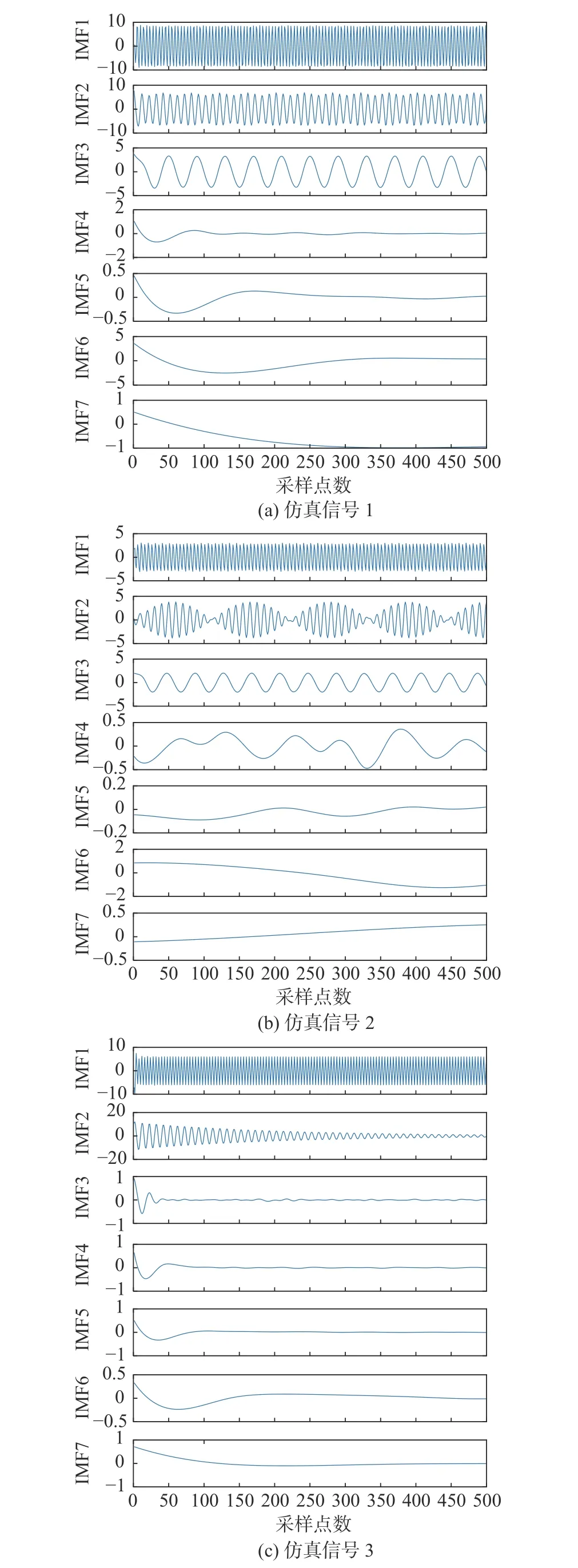
图5 仿真信号CEEMD分解图

表2 KL-CEEMD方法虚假分量识别结果（仿真信号）

由表2可知，仿真信号1和2的前3个分量，以及仿真信号3的前2个分量，与原信号的KL散度值明显小于其他分量，并且与其他分量有数量级的差别，因此与原混合信号的相关性更高。并根据聚类结果，可以明显地看出KL-CEEMD方法可以很好地识别出仿真信号1和2的真实分量为IMF1 、IMF2 和 IMF3，虚假分量为 IMF4、IMF5、IMF6 和IMF7，仿真信号3的真实分量IMF1 和IMF2，虚假分量 IMF3、IMF4、IMF5、IMF6和 IMF7。3种仿真信号真实分量的频谱图、时频图如以及三维图如图6～图8所示。

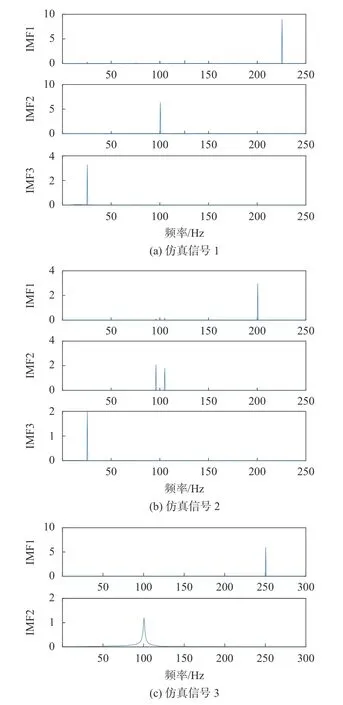
图6 仿真信号真实分量频谱图

图7 仿真信号真实分量时频图

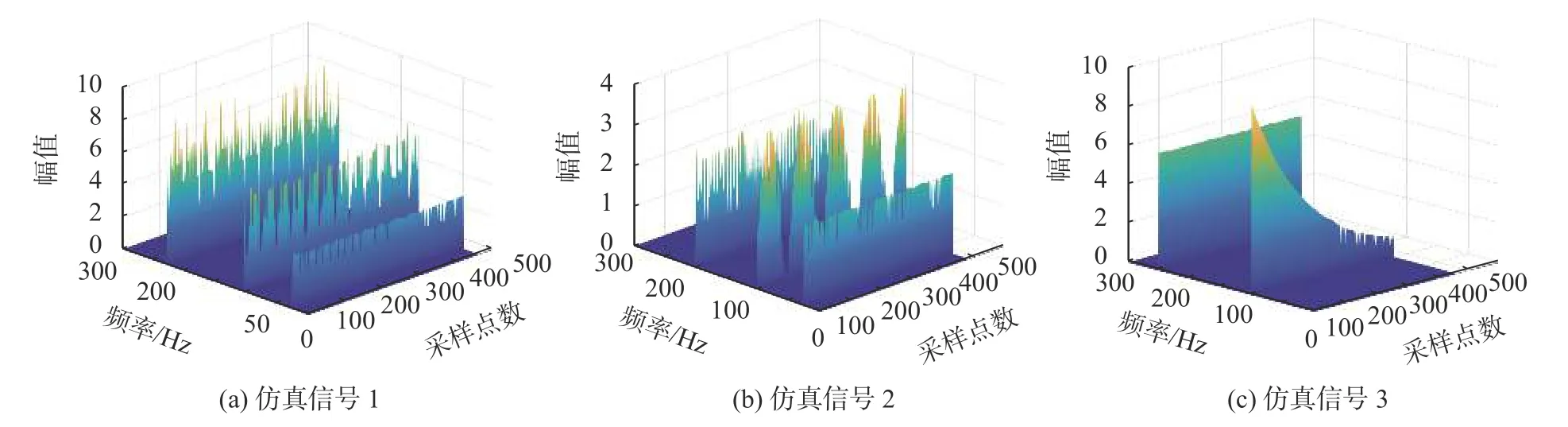
图8 仿真信号真实分量三维图

由图6～图8可以清晰地看出，IMF1、IMF2、IMF3和IMF4的频谱与原仿真信号的频谱图高度相符，显然是CEEMD分解结果中的真实分量。从表2中可以看出，KL散度法和相关系数法都能够区分出真实分量和虚假分量，但相较于相关系数，KL散度的辨别能力更强一些，其真实分量比虚假分量的计算值有数量级的差距。通过以上比较分析，反映了KL散度在区分真假分量时的优越性，由此可判断出KL-CEEMD方法可以准确地识别出仿真信号分解后的虚假分量，也说明了此方法在风机传动系统故障诊断的虚假分量识别方面效果显著。

3.2 实验研究

本章节以风机传动系统实验台的多种故障信号进行实验研究，进一步验证KL-CEEMD方法在风机传动系统故障诊断虚假分量识别中的适用性。采集到的故障振动信号除裂纹和断齿两种以外，还有齿轮缺齿和磨损故障振动信号，下面对4种故障信号进行分析，CEEMD分解图如图9所示。

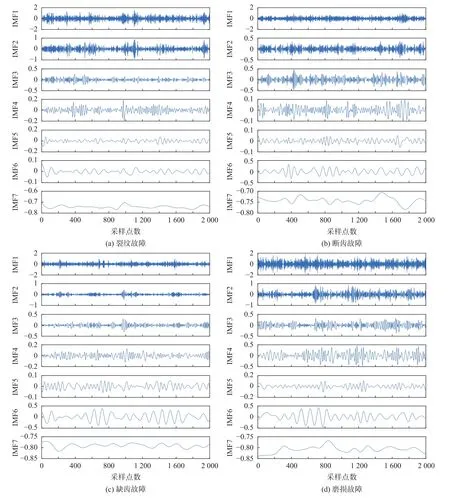
图9 4种故障振动信号CEEMD分解图

4种故障信号的KL-CEEMD方法虚假分量识别结果如表3所示。

表3 KL-CEEMD方法虚假分量识别结果（故障信号）

由表可知，根据对风机传动系统信号的频谱分析和故障诊断经验，基于KL散度指标的聚类结果是完全正确的。所以，基于KL散度的聚类方法可以准确地识别剔除虚假分量，进一步证明了KLCEEMD方法在风机传动系统故障信号处理中起到的显著作用。

因风机传动系统故障信号复杂，故障信号为不平稳信号，并且包含多种冲击信号，如果使用傅里叶变换进行频谱、时频等分析，分析结果误差大，所以本节采用可以处理不平稳信号的边际谱进行分析。去除虚假分量后，信号故障特征真实分量的HHT边际谱如图10所示，其准确反映了原故障信号真实分量的实际频率成分，频率成分清晰分明，容易辨认。而且，通过边际谱图能更准确地对风机传动系统故障种类进行判断，有助于后续进一步进行故障诊断。

图10 4种故障振动信号真实分量HHT边际谱

4 结束语

本文在EMD分解存在模态混叠等问题的前提下，提出了采用CEEMD进行风机传动系统的故障信号特征提取的方法，并针对CEEMD在故障信号处理时出现的虚假分量问题，采用KL散度算法，进一步提出了KL-CEEMD方法。并应用于风机传动系统仿真信号和实验台数据处理中，进行故障信号分析研究。主要结论如下：

1）CEEMD在风机传动系统故障信号处理中有很好的适应性，能够有效分离混合故障信号中的各倍频成分。

2）KL 散度在虚假分量识别中，相比于相关系数法，有更好的辨别能力。基于KL散度的识别方法，在虚假分量识别与剔除中效果更佳。

3）结合聚类分析的KL-CEEMD方法在风机传动系统故障信号虚假分量识别问题中，能够准确地分离出故障信号的时频特性。因此，在机械故障诊断研究中它是一种有效的时频分析方法。