基于时频峰值的光纤陀螺仪信号滤波算法

李晨曦，李国进

（广西大学 电气工程学院，广西 南宁 530004）

0 引言

光纤陀螺仪是基于萨格奈克效应的角速度测量装置，是现代航空、航海、航天和国防工业中广泛使用的一种惯性导航仪器。在实际工作中，由于噪声存在，给测量带来较大的误差。为了滤除噪声，提高精度，研究学者提出了大量的算法，主要算法有卡尔曼滤波[1]、小波滤波[2]、相关向量机[3]、神经网络滤波[4]等。由于光纤陀螺仪的输出并不总是平稳信号，以上算法对进行滤波都存在一定的缺陷。对于非平稳信号而言，瞬时频率描述其频率随时间变化的特性，再加上随机噪声的频率对有用信号的瞬时频率影响不大，可以通过估计含噪信号的瞬时频率来恢复有效信号。在频率估计时，采用伪Wigner Ville分布（Pseudo Wigner Ville Distribution，PWVD算法），对信号进行分析，得出的信号能量在瞬时频率处最为集中，因此可通过取PWVD峰值来估计瞬时频率从而恢复有效信号。

1 时变窗长时频峰值滤波算法

1.1 时频峰值滤波原理

时频峰值滤波（Time-frequency peak filtering，TFPF）算法[5]是由B.Boashash和M.Mesbah两位学者提出的一种基于时频分析理论的随机信号滤波算法。它把含噪信号编码调制为解析信号，采用PWVD算法进行瞬时频率估计，通过求取时频峰值来估计有效信号。对于含噪信对于含噪信号s（t），信号的解析z（t）为：

采用PWVD算法对其进行频率估计，得到：

式（2）中，f是频率，h（λ）是窗函数。取其峰值估计得到瞬时频率：

1.2 时变窗长时频峰值滤波的窗长获取

基于PWVD的TFPF算法的窗函数h（λ）是固定的，导致滤波后的信号仍存在很大的误差。因此，窗函数的窗长如何选择以达到最优的滤波效果就成了关键，为此，本研究采用了一种时变窗长的时频峰值滤波（Time-varying window TFPF，TVWTFPF）算法[6]。

TVWTFPF算法的窗口长度采用数据驱动的方式获得。当窗长为h，时刻为t时，估计的误差定义为：

式（4）中，ω（t）表示准确的瞬时频率值。当瞬时频率的误差比较小时，误差可以表示为一个确定分量和随机分量的和，即：

式（5）中，σh是窗长为h的的标准方差，对于矩形窗来说，可以表示为：

其中，σ2ε为噪声方差，A为信号幅度，T为采样周期，h为窗长；κ为标准高斯分布的分数位。

当选择小窗长时，确定分量可表示为：

则式（5）可表示为：

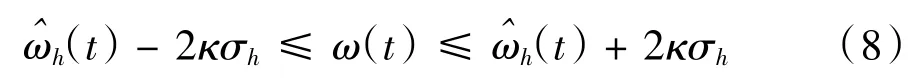
从式（8）可以看出，瞬时频率的精确值ω（t）位于一个置信区间内DK（t），表示为：

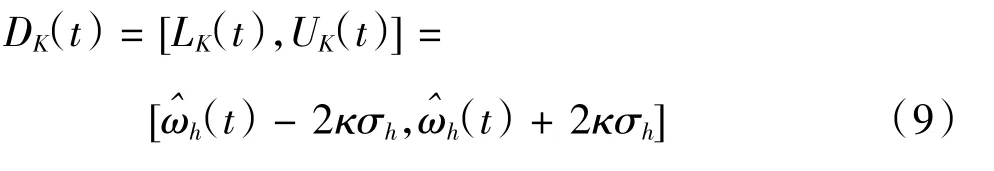
因为相邻窗长间置信度的高低代表了时频峰值出现概率的大小，对于一个递增的窗长序列H={h1＜h2＜h3＜…＜hJ}，当满足下面的两个准则时，取为该时刻的最优窗长。

准则1：若h满足H中Dk-1（t）和Dk（t）有重合点Dk（t）∩Dk-1（t）≠Ø即Dk-1（t）-Lk（t）＞0的最大窗长时，初步将h作为该时刻的最优窗长h*，如图1所示的h*=7。

图1 置信区间交叉准则窗长选择

准则2：在准则1的基础上，考虑Dk-1（t）和Dk（t）重叠部分与Dk（t）的关系：

Ok（t）的取值如下：

1）当Dk（t）⊂Dk-1（t），Ok（t）=1；

2）当Dk（t）∩Dk-1（t）≠Ø时，Ok（t）=0；

3）其他情况下，Ok（t）∈（0，1）。

如窗长为h2时，D2（t）是D1（t）的子集，所以O2（t）=1；当窗长为h3时，O2（t）=0.95。设定一个阀值Otr，当窗长hk满足Ok（t）＞Otr，且是其中的最大窗长时，hk为最优窗长，见图1的h*=3。结合准则1和准则2，得出该时刻的最优窗长为3。

1.3 TVWTFPF算法实现

通过以上分析，采用置信区间交叉准则来获得最优窗长，从而估计得到瞬时频率。TWVTFPF算法具体步骤如下：

步骤1：通过式（1）将含噪信号编码为解析信号；

步骤2：通过式（3）依次求出中每个窗长所对应的瞬时频率估计值；

步骤3：通过式（9）求出该瞬时频率对应的置信区间；

步骤4：当置信区间满足准则1和准则2时，求得该时刻的最优窗长h*；

步骤5：取出在最优窗长h*下所对应的瞬时频率值，最后估计得到有效信号。

2 实验与结果分析

2.1 实验平台

本实验采用MK60DN512ZVLQ10（以下简称：MK60）单片机实时读取数字三轴光纤陀螺仪ITG3200的数据，发送到计算机进行滤波处理后实时显示。ITG3200芯片内含A/D转换器，直接输出角速度数字信号，便于MK60读取。

2.2 静态实验

在静止状态下，陀螺仪水平放置，其三轴的角速度输出均为零，设置采样频率为150 Hz。待陀螺仪信号输出稳定后，分别采样陀螺仪X、Y、Z三轴的信号，用固定窗长的时频峰值滤波算法（以下简称：TFPF）、小波基sym6最大最小值阀值滤波算法（以下简称：sym6）和TVWTFPF的滤波，陀螺仪Y轴输出信号的效果如图2（a）（b）（c）（d）所示。

图2 陀螺仪Y轴输出信号效果

为了更能准确地比较滤波算法的优劣，分别采用均值、方差和信噪比三个指标来衡量滤波的效果，其计算公式分别为：

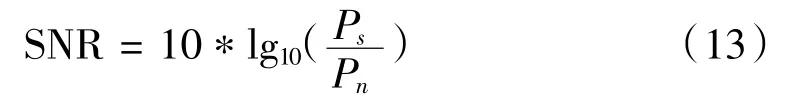
其中Ps是原始信号的功率，Pn是含噪信号的功率。滤波前后数据如表1所示。从表中可以看出，采用TVWTFPF算法Y轴的均值比前两种滤波有所下降。Y轴信号的方差远远小于原始信号，较TFPF滤波和sym6滤波后的信号分别降低了51.5%和50.8%，信噪比分别提高了4 dB和3 dB。相应的X、Z轴信号信噪比较其他两种滤波大约改善3～6 dB。

表1 静止光纤陀螺仪Y轴信号滤波前后性能比较

此外，还对光纤陀螺仪Y轴输出信号Allan方差系数进行了分析，其中量化噪声、角随机游走噪声、偏差不稳定性噪声、速率随机游走噪声、速率斜坡噪声的计算公式如下：

式中Cn（n=1，2，3，4，5）代表的是在最小均方意义下Allan拟合函数下的各个系数。分析结果如表2。

表2 静止光纤陀螺仪滤波前后Y轴输出信号Allan方差系数

从表2可以看出，量化噪声和速率随机游走噪声是影响此光纤陀螺仪信号的主要因素。通过比较三种滤波算法可以得出，TFPF滤波算法减小了量化噪声和速率斜坡噪声，但同时又引进了角随机游走噪声和速率随机游走噪声；sym6滤波算法减小了量化噪声和速率斜坡噪声的影响，但在一定程度上又引入了角随机游走噪声，而采用TVWTFPF算法减少了原始信号的量化噪声、角随机游走噪声、偏差不稳定噪声、速率随机游走噪声和速率斜坡噪声，仅引入了少量的速率随机游走噪声，其滤波远远优于TFPF滤波和sym6滤波，大大提高了光纤陀螺仪的精度。

2.3 动态实验

为了更准确地表现本研究所用算法的性能，动态实验把光纤陀螺仪固定在匀速转台上，转台由MK60单片机驱动并设置转速。转台从静止开始慢慢带动陀螺仪达到10 deg/s的速度，保持此速度匀速旋转一段时间后速度缓慢地变为零，采样频率是150 Hz。实验结果如图3所示，其中0～160 s是陀螺仪缓慢加速时间，160～360 s是陀螺仪保持10 deg/s匀速旋转时间，360～560 s是缓慢减速时间。由图3可以看出，TVWTFPF滤波后的信号更趋向于陀螺仪的速度，且波形更加的平稳。

图3 TVWTFPF滤波后Y轴输出信号

为了能更加清楚地看到在速度突变的情况下滤波的好坏，图4给出了陀螺仪在转速度为10deg/s匀速旋转下突然减速的局部波形比较图。由图4可以清晰地看到，小波sym6和TFPF滤波后的信号不能实时地跟踪原始信号，偏差比较大，且存在一定的延迟，而采用TVWTFPF滤波后的信号能很好地跟踪原始信号。

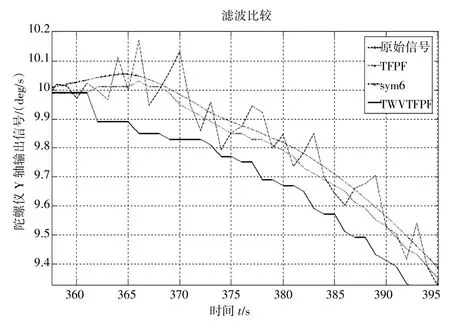
图4 各滤波算法比较

3 结束语

文中采用一种时变窗长时频峰值滤波算法，进行光纤陀螺仪的随机去噪。结果表明：在静态或动态下，采用时变窗长时频峰值滤波算法对光纤陀螺仪进行去噪，减小了信号的输出噪声，提高了输出信号的信噪比，能实时地跟踪原始信号，减小陀螺仪的输出误差。