基于支持向量机的新能源台区相户关系辨识方法

蔡志宏，吴杰康，王瑞东，李红玲，陈盛语，蔡锦健，张宏业

(广东工业大学 自动化学院，广州 510006)

0 引 言

随着全球能源互联网的不断推进和“碳中和”倡议的持续发酵，电力行业面临着新的机遇和挑战。新的发展、新的诉求对电力营销、调度、配网等环节的发展也提出了更高的要求。智能电网是近些年来电力工业最重大的变革与创新，也是智慧城市建设的重要组成部分之一[1]。同时，智能电网的快速发展也对配电网侧的精细化管理提出了更高的要求[2]。传统的低压配电网运维管理由于缺乏拓扑信息的支撑容易导致电压质量治理效率低下，故障抢修不及时，自动化水平较低[3]。因此，提出精准且高效的台户关系辨识方法，对实现智能配电网台区管理运行的“信息化、自动化、精准化”具有重要意义。

目前低压配电网的拓扑辨识主要包括信号法、数据标签法和大数据分析法。信号法是通过在低压台区注入电压或者电流特征信号，根据用户侧反馈信号辨识相户之间的关系[4]；数据标签法则是根据低压配电网的设备进行逻辑编码，实现拓扑关系动态管理[5]。以上两种方法依靠众多的通信设备和终端设备，对于仪器本身的精确度要求高，且投资成本大，维护较困难。

大数据分析方法是基于高级量测体系获取的量测信息，通过数学方法和智能算法对电气量进行数据挖掘，实现低压配电网拓扑自动辨识[6-8]。依据量测装置所采集的电压数据，一方面通过对台区用户智能电表中电压数据波动趋势的相似性分析，利用灰色关联分析来实现用户归属台区及相别辨识[9-10]，某些情况波动趋势相似性存在重叠，难以辨别所属相别；另一方面采用FastI CA技术对电时序数据进行独立成分分析(independent component analysis，ICA)及特征提取，对特征数据进行K-means聚类分析，实现台户辨识[8]，但所需数据量过于庞大，辨识耗时较长。针对台区线变不匹配问题，文献[11]提出了一种考虑异常点的台区用户相别辨识方法，通过局部异常因子算法剔除非分析台区的用户数据，并采用改进K-means算法对属于分析台区的用户进行相别辨识，取得了不错的效果。就邻近台区数据信号互相干扰的问题，文献[10,12]提出了一种基于大数据的改进灰色关联分析的智能台区识别方法，通过关联度来判断电能表的台属性，排除邻近台区数据干扰，实测证明该方法有效提高台区识别的精准度，但是复杂情况下精准度有待提高。目前台区用户相属辨识大部分针对普通用户，忽略了电动汽车和可再生能源的渗透率不断增加对用户相属辨识的影响。

针对上述问题及现有辨识方法所存在的缺陷，该文提出一种融合改进T型关联度和支持向量机的两阶段辨识模型，考虑电动汽车充放电的随机性和新能源出力的不确定性，采用随机模糊理论构建风、光在各种场景下的出力模型，建立电动汽车随机参数的概率密度函数，并重构用户的电压时间序列，利用两阶段辨识模型对单一风、光场景和多风、光场景下的电动汽车用户进行相户辨识。

1 分布式电源发电对电压的影响

由于新能源电源接入低压台区用户端，新能源用户出力具有随机性和不确定性，也就是新能源数据收集过程中产生的“噪声”，因此，单纯用一组或者多组预测到的风、光功率数据作为特征数据，无法完全学习到风、光出力的所有特征，导致出现台户关系辨识精度不高的问题。该文利用随机模糊理论来构建风、光的随机模型。

1.1 随机模糊理论

随机模糊模拟是在随机模糊环境下的模拟理论，其变量既有随机性又有模糊性。如果仅仅是简单地考虑这些变量的随机性，而忽视它们所具有的模糊性，最后的处理结果就有可能不够精确。随机模糊变量是指从可能性空间到随机变量构成集合的可测函数，随机模糊变量本质上是取随机值的模糊变量。

模糊随机变量是随机模糊模拟的一种数学描述，它是从概率空间到模糊变量构成的集类ζ的可测函数[13]，其实质是一个取值为模糊变量的随机变量。假如η是概率空间(Ω,A,Pos)上的随机变量，μ是模糊变量，并且ζ(ω)=η(ω)+μ,∀ω∈Ω，如果对于R上的任何Borel集，Pos{ξ(ω)∈B}是ω的可测函数，则ξ=η+μ是一个模糊随机变量。类似地，定义ξ(ω)=η(ω)μ,∀ω∈Ω。

1.2 光伏发电的随机模型

光伏发电技术是使用光伏电池利用太阳能的一种发电技术，光伏发电消耗的能源是太阳能，所以光伏电池发电功率容易受到诸多自然条件和因素的影响。光伏电池的表面温度、环境温度和湿度、光照强度等自然因素都会影响光伏电池的发电功率。相关研究和统计表明，太阳光照强度在一定时间内服从Beta分布，使用Beta分布的光照强度表示光伏电池出力的随机性，太阳能光照强度的概率密度函数为[14]

(1)

式中：E表示实际光照强度；Γ表示Gamma函数；a和b分别表示Beta分布的形状参数。

1.3 风电机组的随机模型

风力发电功率主要受风速的影响，而风速也因风力发电机所在海拔、不同时刻、不同地点的差异而产生较大变化，在相同地点由于不同时刻气候变化的原因，风速也会发生变化，风机发电功率因为风速的不确定性而具有随机性。目前研究中，研究者常用双参数Weibull分布来表示风速的随机性，使用Weibull分布的风速表示风机发电功率的随机性，双参数Weibull分布概率密度函数[15]为

(2)

式中：v表示实际风速；k和c分别表示Weibull分布的形状参数和尺度参数。

2 电动汽车充放电对电压的影响

2.1 电动汽车充放电特性

电动汽车数学模型建模方法主要包括单一建模、物理学建模、统计学建模。假定1天中电动汽车并网时间、离网时间、充电功率是相户独立的随机变量，融合多台电动汽车的差异，考虑离并网时间、日行程量等常规因素，采用统计学建模方法[16]对电动汽车负荷进行建模，进而重构用户的电压时间序列。

2.1.1 建立离并网时刻、日行程量的概率密度函数

并网时刻是指电动汽车在1天中起始接入电网充电的时刻；离网时刻指电动汽车在1天中结束充电行为，脱离电网的时刻。基于美国联邦公路局的美国家用车辆调查结果(national household travel survey，NHTS)[17]，近似认为离并网时刻服从正态分布，日行程量服从对数正态分布[18]，进行拟合处理后，分别得到如下的离并网时刻、日行程量的概率密度函数：

(3)

(4)

(5)

式中：x均表示时刻1～24 h；fo是离网时刻的概率分布函数，μo=8.92，δo=3.24；fi是并网时刻的概率分布函数，μi=17.6，δi=3.4；fk是电动汽车的日行程量的概率分布函数，δk=2.98，μk=1.14。

2.1.2 拉丁超立方抽样

由于电动汽车数据量众多，为了便于统计其充放电规律，采用NJW频谱聚类批量管理电动汽车充放电。

通过拉丁超立方抽样[19]获得每辆电动汽车的参数：入网时间Tstart,j、离网时间Tend,j、结束荷电状态SOCend，得到所有电车数据集X={x1,x2,…,xn}，这些代表了电动汽车的需求信息。NJW频谱聚类主要为以下步骤：

1)构建相似矩阵K。将电车数据集进行极值归一化，根据式(6)计算数据点间的欧氏距离，再根据式(7)计算两点间的高斯距离，进而构成相似矩阵K。

Dij=‖xi-xj‖

(6)

(7)

2)根据相似矩阵K构造拉普拉斯矩阵L，进一步构造正则化拉普拉斯矩阵Lsym。

3)计算Lsym的前i个最大特征值对应的特征向量{u1,u2,…,ui}，将其作为各列构造矩阵，将矩阵的行向量转化为单位向量，得到矩阵B，将矩阵的每一行看做一个点，使用K-means算法将其划分为i个类簇。

聚类完成后，具有相似特征的电动汽车被归为一类，同一组的电动汽车由聚合器统一管理，聚合器的出力限制，离并网时间以及结束时荷电状态以聚合器内所有电动汽车的几何中心表示。

2.2 电动汽车充放电功率分布模型

考虑到电动汽车既能作为负荷，也能通过合理的管理策略作为储能进行放电，该文融合用电成本、收益等因素，通过构建混合整数线性规划模型(mixed integer linear programming model，MILP)求解电动汽车用户在3种充放电策略下的功率-时刻分布规律。3种用户电动汽车充放电策略的数学模型如下所述：

2.2.1 无价格引导的电动汽车充电

策略1为电动汽车充电时采用传统即插即充策略，式(8)～(12)为其数学模型。该策略下的电动汽车用户在充电时不考虑电价及用户售电收益，并且不考虑电动汽车的放电行为。

(8)

(9)

(10)

(11)

(12)

2.2.2 基于价格引导的电动汽车充电

策略2为电动汽车充电时考虑电价进行选择性充电，式(13)～(14)为其数学模型。该策略下的电动汽车用户在电动汽车充电时考虑市场电价的引导，通常会选择在低电价时段进行充电，以达到充电费用最小。策略2相较于策略1在时间上平移了充电负荷分布。

(13)

(14)

2.2.3 基于价格引导的电动汽车充放电

策略3为电动汽车充放电行为选择“低价充电、调度放电”的模式，式(15)～(16)为其数学模型。该策略下的电动汽车用户不仅考虑市场电价因素进行适时充电，而且参与电网调度。一方面降低充电成本，另一方面作为储能售电赚取市场差价。与策略1、2相比较，策略3更符合未来社会发展的方向。

(15)

(16)

根据以上构建的3种电动汽车充放电策略，通过求解出MILP问题得到电动汽车的充放电功率-时刻分布图,如图1所示。

图1 3种策略下电动汽车充放电功率-时间分布Fig.1 Power-time distribution of EV charge and discharge under three strategies

2.3 考虑电动汽车充放电影响的电压时间序列

用户通常的用电对象是指家用电器、照明装置等。由于小区的智能化、环保化发展，电动汽车成为每家用户不可或缺的交通工具，与此同时可再生能源发电也逐渐进入各家各户。如图2所示，负荷功率流经电力线路的有功功率损耗和无功功率损耗是造成用户侧电压时序波动的主要原因，因此，需要重新构建用户电压时间特征。

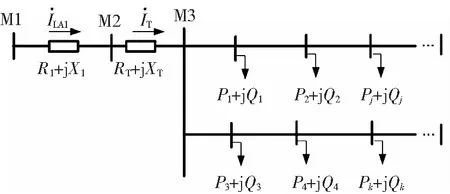
图2 台区相户等值电路图Fig.2 Equivalent circuit diagram of station area phase-household

由1.2节和1.3节得到风、光发电随机模型，为了使训练模型更加贴合实际的应用场景，对风、光场景进行如下处理：根据晴空指数及太阳高度角等特征进行模糊聚类，把太阳辐射天气划分为9类[20]；根据风电天气的气压、风速、风向、云量等指标，把风电天气分为4类[21]。对以上获得的风、光场景进行顺次匹配，共有36种可再生能源出力场景。结合3种策略下电动汽车充放电功率分布规律(如图1所示)和可再生能源的出力场景，依据馈线横向、纵向压降式(17)求出电压时间序列波动量，通过与用户原始负荷电压数据耦合得到重构后的电压时间序列(式(18))。

同一个台区下的用户所在供电半径可近似看作是相等的，该文统一假设台户间的输电线路型号为LGJ120/20，R=0.249 6 Ω/km，X=0.347 Ω/km。计算电动汽车充放电、可再生能源发电引起的电压波动：

(17)

(18)

3 相户关系的两阶段辨识

3.1 台区的电压特征序列

对于电压时间特征序列X0=(x0(1),…,x0(n))，相关因素序列X1=(x1(1),x1(2),…,x1(n-1),x1(n))。令yi(k)=xi(k)-xi(k-1),i=0,1,k=2,…,n表示电压时间序列从时刻k-1到时刻k的电压增量，记Di为序列Xi在各个时段的增量绝对值的算数平均值，则zi(k)表示Xi在各个时间段的增量绝对值。

改进T型关联度是基于灰色关联度和T型关联度两者进行改进，它克服两者的缺点综合考虑因素的时间序列曲线变化势态的接近程度和各因素的时间序列曲线的变化率[22]。其计算过程如下：

(19)

(20)

定义2个因素从时刻k-1到时刻k的关系数为ξ0,1(k)，即

(21)

式中：符号函数sgn(z0(k)z1(k))反映2个因素的正负相关性，当z0(k)z1(k)≥0时，ξ0,1(k)≥0，说明2个因素的时间序列正相关；否则为负相关。α称为分辨率，α值越小，相关系数的分辨力越大。

改进T型关联度r计算方法为

(22)

当-1≤r<0时，X0和X1为负相关，且r负值越小，负相关程度越高，反之也成立。

3.2 基于支持向量机的相户关系辨识

支持向量机的基本思想为：针对线性可分问题，通过构建最优分类超平面实现二分类问题；针对线性不可分问题，通过非线性变换方法将样本从原空间投影到高维特征空间，转换为线性可分问题[23]。

假设样本集为{(xi,yi)|i=1,2,…,N}，xi∈Rn，yi∈{-1,1}表示样本标签，则最优二分类超平面为

WΦ(x)+b=0

(23)

式中：Φ(x)为非线性变换。

(24)

支持向量机核函数的选取对分类结果影响深远，常用的核函数有线性核函数、多项式核函数和径向基核函数等。根据实际场景，该文选取高斯径向基核函数，其定义为

(25)

式中：|X-Y|为向量之间的距离，σ为常数且σ≠0。

3.3 求解步骤

该文提出一种联合改进T型关联度与支持向量机的两阶段辨识方法，该方法能够有效准确地对“36种风、光场景和3种电动汽车充放电选择”的108种混合用户进行台户关系辨识。第一阶段辨识通过计算已知相属关系的用户电压改进T型关联度，选取其平均值作为判断该相所属用户的改进T型关联度阈值P。对未知相属关系的待测电动汽车用户进行改进T型关联度计算，若r>P则此用户属于该相，否知视为可疑用户。对于可疑用户进行第二阶段的辨识，利用训练好的支持向量机辨识模型进行辨识。具体的辨识过程如图3所示。

图3 相户关系辨识流程图Fig.3 Identification flow chart of phase-household relationship

4 试验分析

该文选用广州某小区台区下三相用户的电压时间序列数据，三相共选择其中103个用户，择取对称数据每相20户作为训练数据。由电动汽车的离并网时刻以及行程分布，采用NJW频谱聚类，得到各种管理策略下的充放电功率分布，如图1所示。同时，根据风、光的概率密度函数进行随机抽样并模糊化处理，循环抽取1 000×1 000组数据。该台区下光伏发电功率约为300 kW，风力发电约为90 kW。基于随机模糊理论，为了使所训练的辨识模型能够在多种混合模式下进行高准确度的辨识，用户电压数据更加贴合实际情况，设置了3种电动汽车充放电策略以及36种新能源出力随机组合案例作为训练数据。

4.1 单风-光-车场景的两阶段辨识

针对以上设定的场景，选择策略1下的电动汽车和任意一组风、光新能源出力序列重构用户电压时间序列，分别计算三相下共103户(A相户号1～22，B相户号23～46，C相户号47～103)的改进T型关联度系数，结果如图4所示。

该案例设置A、B、C三相各20个用户作为训练集，剩下的用户作为测试集。由图4可知，在A相中前1～22个用户的关联系数基本上是最高的，说明该关联系数具有一定的物理意义。但是B相中存在个别用户关联系数比A相某些用户关联系数更高，难以精确辨识。根据该文设置的辨识流程：1)计算已知用户的关联系数平均值；2)抽取测试集中A、B、C相用户作为待辨识用户，并选出小于均值的用户作为可疑用户；3)对可疑用户采用支持向量机训练模型，最终输出可疑用户相别，并查验。

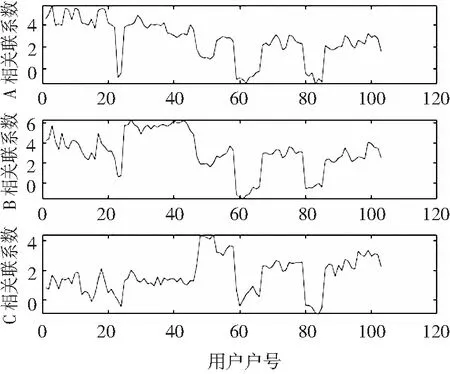
图4 三相用户的改进T型关联系数Fig.4 Improved T correlation coefficient for three-phase users

通过多次试验，选取A相已知的20个用户整体关联度平均值(P=4.635 1)作为判别可疑用户的阈值，可以完全确保把可疑的用户筛选出来并进行进一步的辨识。辨识结果能够准确判别待辨识用户的相位，如表1所示。在测试集中，21号用户整体T型关联系数大于阈值，可直接认定为A相下的用户；22号用户整体T型关联系数小于阈值，通过输入用户电压时间特征序列到支持向量机所训练的模型中，输出该用户属于A相；其余测试集的用户由于整体T型关联系数小于阈值，通过支持向量机训练模型辨识用户相别归属，经查验，准确率为100%。

表1 单风、光场景辨识结果Table 1 Single wind and light scene identification results

4.2 多风-光-车场景的两阶段辨识

实际情况中，除了电动汽车充放电具有随机性以外，新能源出力的不确定性也会影响台户关系辨识的精度。对4.1节的测试集的用户随机添加风电、光电出力场景并重新进行10次测试，测试结果如表2所示。风、光的波动在一定程度影响用户与该相整体的关联度，但它们的关联系数仍然在阈值范围以下。进一步利用4.1节预测到固定场景下的风、光出力所训练得到的辨识模型辨识以上测试用户，测试结果如图5所示。

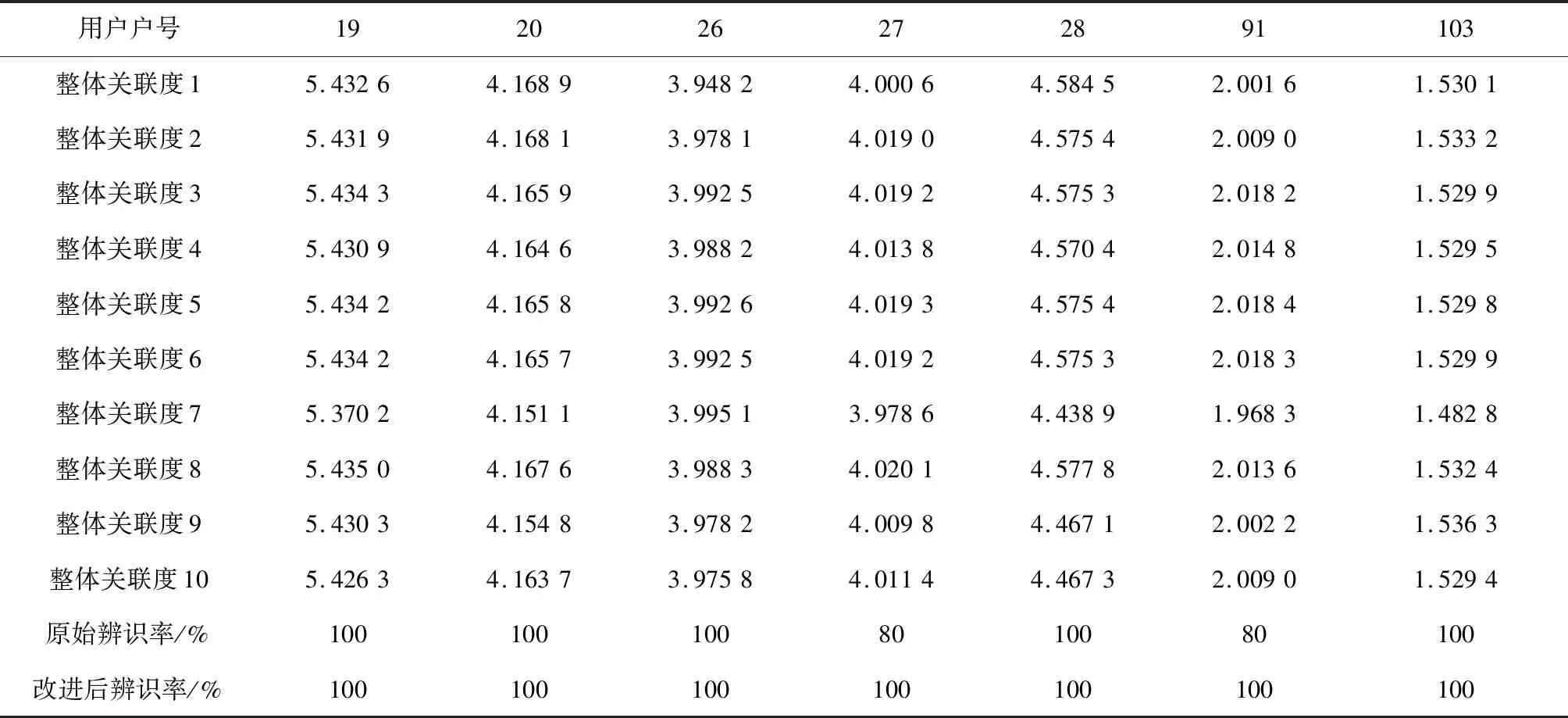
表2 多风、光场景辨识结果Table 2 Multiple wind and light scene identification results

由图5辨识结果可得：随机抽取10个场景下的风、光出力重构用户的电压时间序列作为特征测试集，对21、22、26、27、28、91、103号用户进行相属辨识。由于辨识模型是在单一风、光场景下训练得到的，其对于多风、光场景的辨识效果较差。例如：27号用户本属于B相用户，在进行第4个、第6个风、光波动场景测试时，模型辨识结果为C相；同理，91号用户本属于C相，在进行第6个风、光波动场景测试时模型辨识结果为B相。因此，单一风、光场景所训练得到的辨识模型无法辨识多风、光场景的电动汽车用户相户关系。

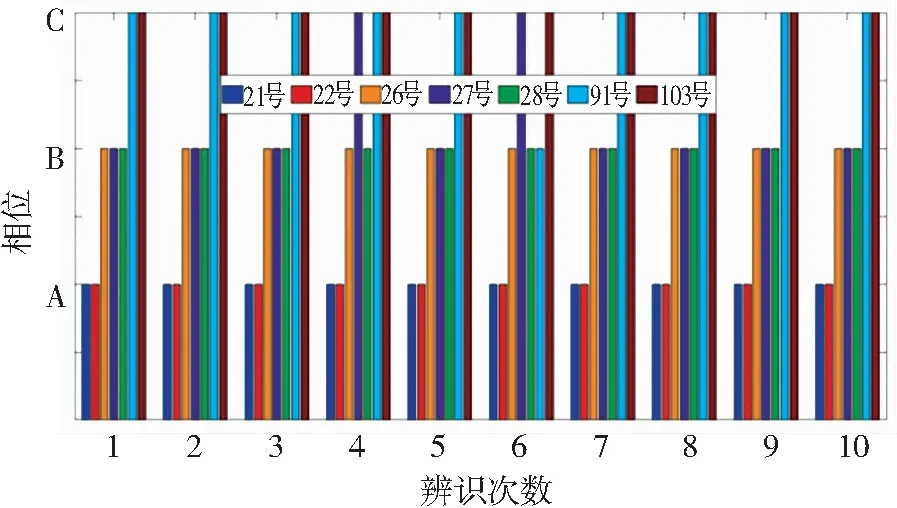
图5 多风、光场景的相属辨识结果Fig.5 Identification results of multiple wind and light scenes

根据随机模糊控制理论以及风、光场景的分类，构建36种风光场景和3种电动汽车充放电策略下的电压时间序列作为新的训练集，共产生36组3×60×90维的数据，采用支持向量机重新训练新的辨识模型，得到改进后的训练模型，重新辨识4.1节中的测试集用户，辨识结果如图6所示。

由图6辨识结果可得：21、22号用户归属于A相；26、27、28号用户归属于B相；91、103号用户归属于C相。经查验原始标签，辨识结果准确率为100%，且该模型具有良好的稳定性。基于多风、光场景下的用户电压特征数据，分别选择A相(21～22号)、B相(43～46号)、C相(67～103号)用户作为测试集，采用不同的智能算法进行辨识，辨识结果如表3所示。根据表3可知，相较于其他的辨识方法，该文所述的辨识方法的辨识准确率能够达到100%，更优于支持向量机、决策树和KNN。

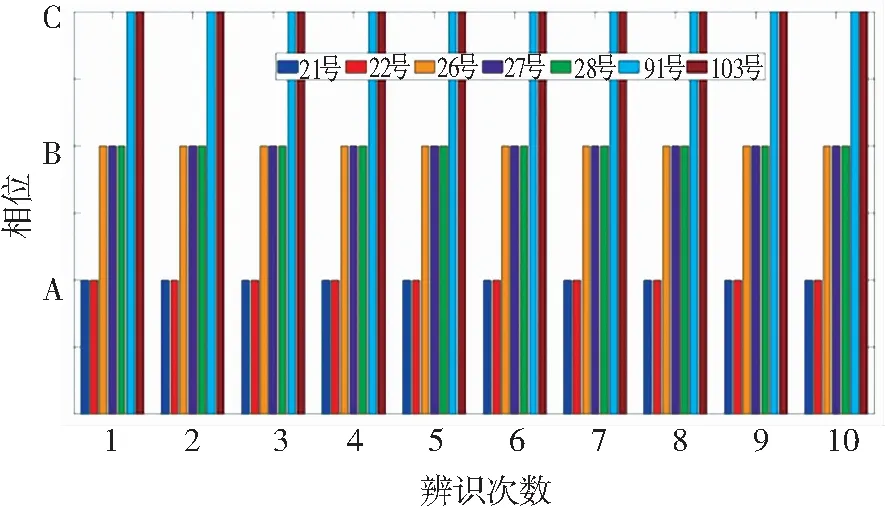
图6 改进后的相属辨识结果Fig.6 Improved phase assignment identification results

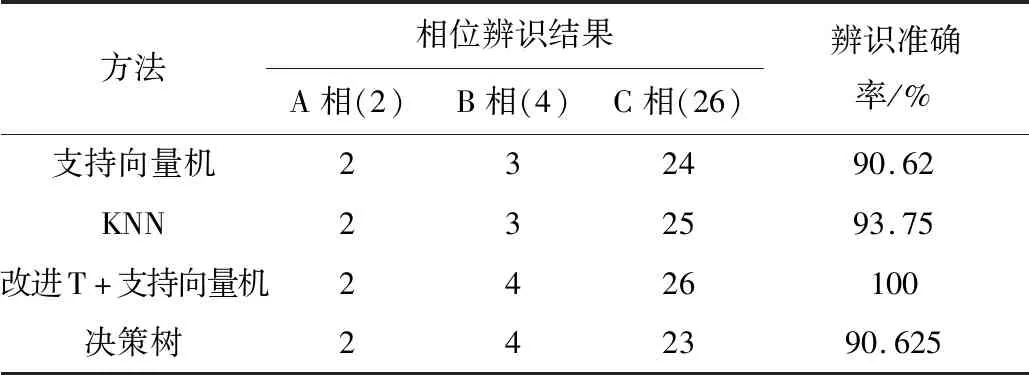
表3 多种辨识方法的辨识精度对比Table 3 Identification accuracy comparison of multiple identification methods

5 结 语

该文针对电动汽车充放电与风、光出力不确定性场景下的台户关系相户辨识准确率低、稳定性差等问题，运用改进T型关联度和支持向量机算法识别用户所属相别。所建立的模型具有以下特点：

1) 改进T型关联度算法克服了传统灰色理论结果容易失真，无法准确反映用户电压时间序列波动率的缺点；

2) 利用随机模糊理论所构建的风、光随机模型融合了随机性和模糊性特征，更加贴合实际情况；

3) 综合考虑电动汽车在不同充放电策略下的充放电情况以及多种风、光场景的融合，重构用户电压时间序列特征向量；

4) 所述的辨识方法能够同时精准辨识单风-光-车场景和多风-光-车场景下的用户相户关系，具有实用性和可靠性。