基于时间响应函数修正的GM（1，1）模型及变形预测应用

邱利军，张 波，周占学，陈学良

（1.河北建筑工程学院 土木工程学院，河北 张家口 075000； 2.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000； 3.中国地震局地球物理研究所，北京 100081）

灰色系统理论自邓聚龙教授于1982 年提出至今，其应用已经拓展至各行各业。 基于该理论的深入研究从未中断［1］，而作为该理论核心的GM（1，1）模型是研究最活跃的模型之一［2］，并且在理论研究与实践应用中取得诸多成果。 鉴于传统建模方法存在缺陷，很多学者进行了模型改进，以达到更好的预测效果［3-4］。部分学者采用改进原始序列光滑度的方法使预测精度提高，其中：陈涛捷［5］对原始序列进行对数变换以改变其光滑度，提高了模型预测精度；于德江［6］提出开方变换的方法来改进序列光滑度，从而提高模型预测精度；何斌等［7］进行指数变换以提高序列光滑度，拓宽了模型应用范围，并在理论上证明了其优越性；关叶青等［8］采用三角函数变换改进序列光滑度。 部分学者采用变换初始值的方法对模型进行改进，其中：党耀国等［9］以x（1）（n）为初始值建立GM（1，1）模型，并证明其较原始模型优越；尹方平［10］提出以αx（1）（n）为初始值的GM（1，1）模型，并给出参数α的计算公式，以此提高预测精度。 部分学者对背景值进行改进，其中：谭冠军［11］认为背景值是直接影响GM（1，1）模型精度和适应性的关键因素，提出将区间n等分所得面积近似为区间面积，以其作为背景值的方法，并给出了求解等分值n的试探法和经验公式法；李俊峰等［12］用牛顿-柯特斯公式重构模型中的背景值以改进算法模型。 而在 实践 应 用 中，王 艳 艳 等［13］将 传 统 均 值GM（1，1）模型应用于小浪底水利枢纽大坝变形预测中；邱利军等［14］对光滑度进行改进并采用实测基坑变形数据及隧道变形数据进行了验证；文建华等［15］采用重构参数改进GM（1，1）模型并对隧道收敛变形进行预测；刘光秀等［16］采用GM（1，1）模型与Gompertz 曲线加权组合以预测路基沉降；牛景太［17］在新陈代谢的基础上改进背景值，并应用于土石坝变形预测。

综上，在模型改进方面，大多数学者从提高拟合精度的角度进行了研究，而笔者认为可以从拟合所得时间响应函数与实测累加曲线存在残差这一角度对其进行修正，提高除建模序列之外的后期序列的预测精度。因此，笔者提出对一次累加序列拟合所得时间响应函数进行平移旋转变换，得到新的函数，并进行预测。

1 GM（1，1）模型及修正

设原始数据序列X（0）＝｛x（0）（1），x（0）（2），…，x（0）（n）｝（n为数据总数）为非负离散序列，而X（1）＝｛x（1）（1），x（1）（2），…，x（1）（n）｝是X（0）的1-AGO 序列，那么X（1）的紧邻均值生成序列为Z（1）＝｛z（1）（2），z（1）（3），…，z（1）（n）｝，则GM（1，1）模型为

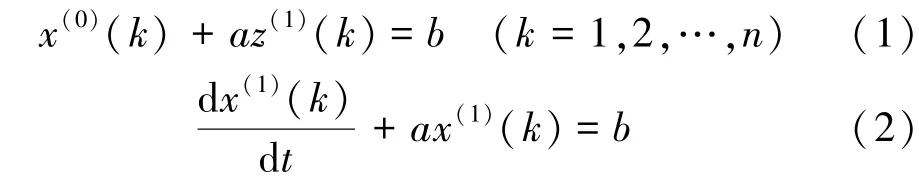
式中：a、b为待求灰参数；t为时间。

式（2）称为式（1）的白化方程。

设

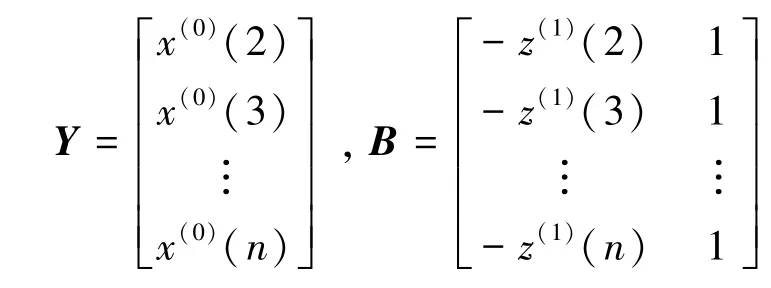
用最小二乘法可求得

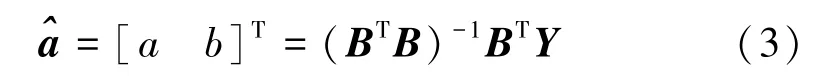
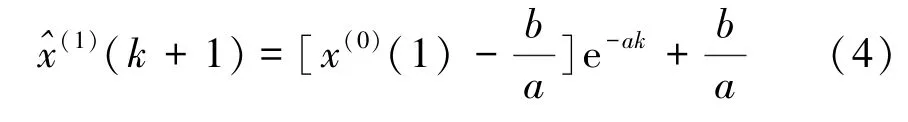
式（4）即X（1）序列预测公式（时间响应函数），若k+1≤n则函数值为拟合值，若k+1＞n则函数值为预测值。

时间响应函数值与实测累加曲线并不重合，当k+1＞n时，为了得到较精确的预测值，对式（4）进行变换。 变换的方法：假设横轴表示时间（周期）序列，而纵轴表示一次累加值，在该平面坐标系内先将式（4）计算 所 得 的 曲 线 平 移，使 得（n，＾x（1）（n）） 与（n，x（1）（n）） 两个点重合， 而后将 平移后曲线绕点（n，x（1）（n）） 旋转θ角，得到新的预测曲线。

时间响应函数的平移量Δ计算公式为

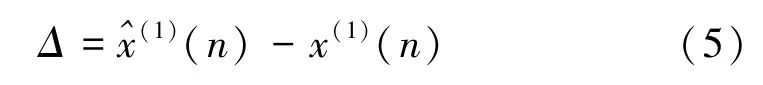
若Δ＞0，则式（4）计算所得曲线下移，反之则上移。 其平移后公式为

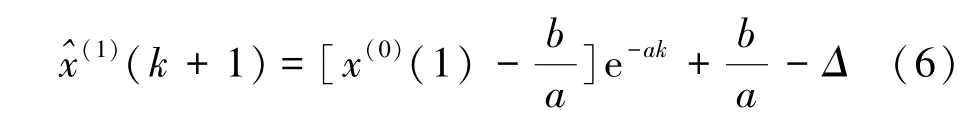
进而计算旋转角θ（对曲线函数y求在横坐标为n处的导数得到斜率，n-1期点与n期点构成直线斜率近似代替实测累加曲线斜率，求其反正切值的差值，即夹角值）：

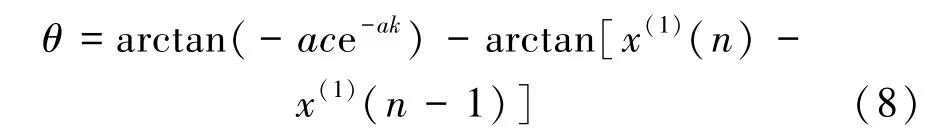
若θ＞0，则平移后进行顺时针旋转；若θ＜0，则在平移后进行逆时针旋转。

由于旋转角θ一般较小，因此短期预测可采用原模型求得的拟合预测曲线上第n期与第n+1 期所连直线斜率计算反正切值，取代式（8）中等号右侧第一项并对曲线函数求导后计算反正切的结果，从而近似得到θ值；或直接采用原模型求得拟合预测曲线上第n-1 期与第n期所连直线斜率，计算反正切值取代式（8）中等号右侧第一项并对曲线函数求导后计算反正切的结果，求得近似θ值。

设坐标系中任一点坐标为（x，y），其绕点（x0，y0）旋转θ后得到新的点坐标（x′，y′），对应转换公式为

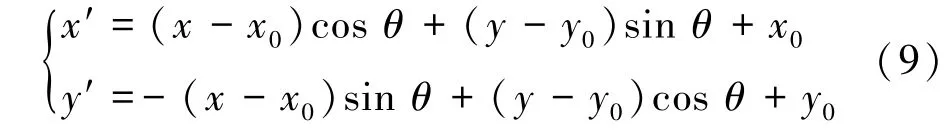
由式（9）可知，将（x′，y′）回转θ后可得到（x，y），其公式为

根据公式（10），若曲线上任一点都旋转θ，则结合公式（7）可得绕（n，x（1）（n））旋转变换后的曲线公式，即

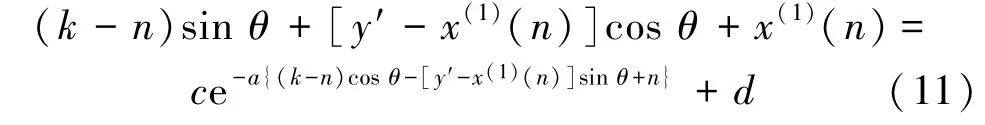
公式（11）即变换后所得的新的时间响应函数。对其进行调整得

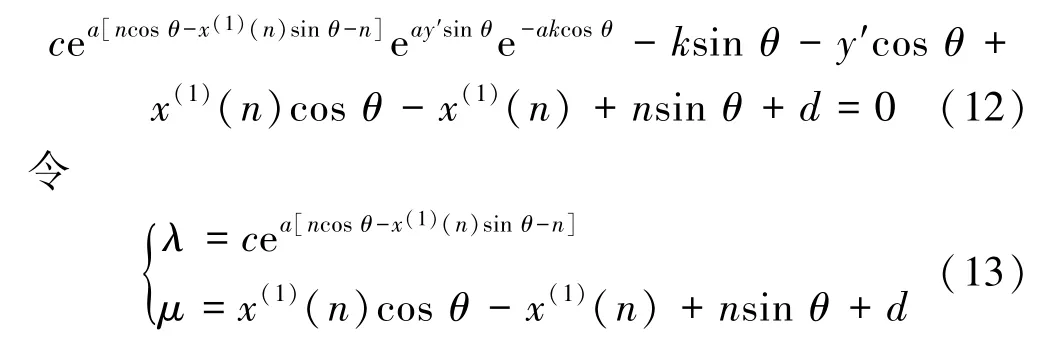
则

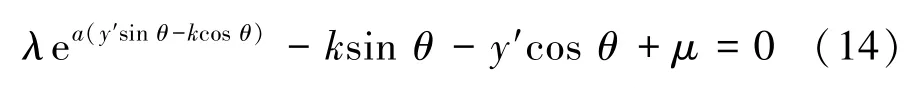
公式（14）即建立的旋转后y′（即＾x（1）（k） ）与横坐标（k）对应的方程，代入对应的k值后求解y′的一元非线性方程，可得到对应的累加预测序列，即

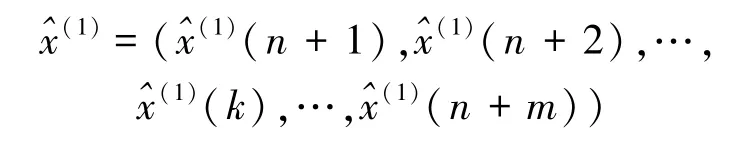
根据公式（14）求得一次累加预测序列，再进行累减还原即可求得预测值：

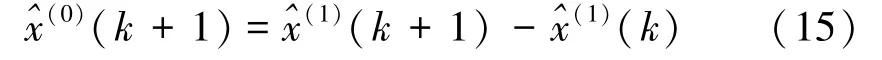
灰色GM（1，1）模型预测本质为指数函数预测，可知公式（7）为GM（1，1）模型一般形式，该修正方法可推广至符合指数函数形式的所有GM（1，1）模型。 其修正原理如图1 所示。

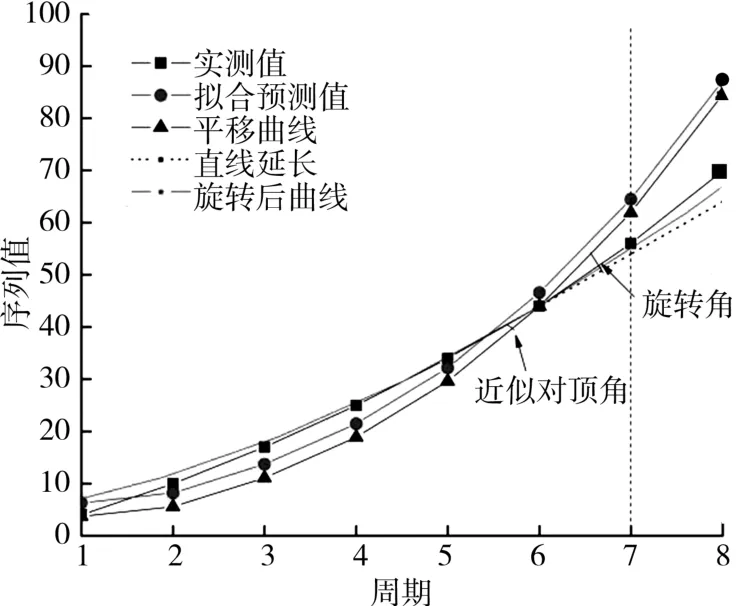
图1 GM（1，1）模型修正原理示意

由图1 可知，实测累加序列与拟合累加序列曲线在后期可能出现相近、相交或相离的情形，旋转角的正负控制其旋转方向。 由于近似求得的夹角与实际存在偏差，因此可能出现预测校正过量（如图1 所示）或校正不足的问题，但整体是在预测期向实测累加曲线靠近，以减小预测误差。 但可能使得建模已知序列拟合值因旋转而失真，导致与已知值相差较大，因其为已知值，故不作考虑。

2 实例应用

2.1 实例一

选取文献［13］中小浪底水利枢纽大坝坝顶监测点807 点观测数据，8 期数据中以前5 期数据进行建模、后3 期数据进行验证。 观测点实测累计变形建模序列见表1。 分析过程中采用传统均值GM（1，1）模型（模型一）、对数变换均值GM（1，1）模型（模型三）、以x（1）（n）为初始值的GM（1，1）模型（模型五），对这3种基本模型分别进行时间响应函数修正（分别对应模型二、四、六），得到修正后的预测结果并进行比较。

表1 实例一实测建模数据序列值 mm

经过多种模型建模预测，以预测相对误差表示模型预测精度，结果见表2。 需要说明，所有模型采用C＃程序设计语言实现，中间变量采用双精度浮点型（double）变量，表中最终结果采用四舍五入取至小数点后两位。

表2 实例一不同模型预测值与实测值比较分析

根据表2 分别比较模型一和模型二、模型三和模型四、模型五和模型六预测结果，发现对均值GM（1，1）模型、对数变换后均值模型及以x（1）（n）为初始值的均值模型进行时间响应函数修正后的预测精度较原模型均有所提高，说明对模型的时间响应函数值进行修正，能使其与实测累加曲线更接近，从而提高预测精度。 再比较模型二、模型四、模型六可知，模型二与模型六预测精度相近，而模型四精度较高。

绘制各模型预测曲线与实测曲线对比图（自第5期开始），如图2 所示。

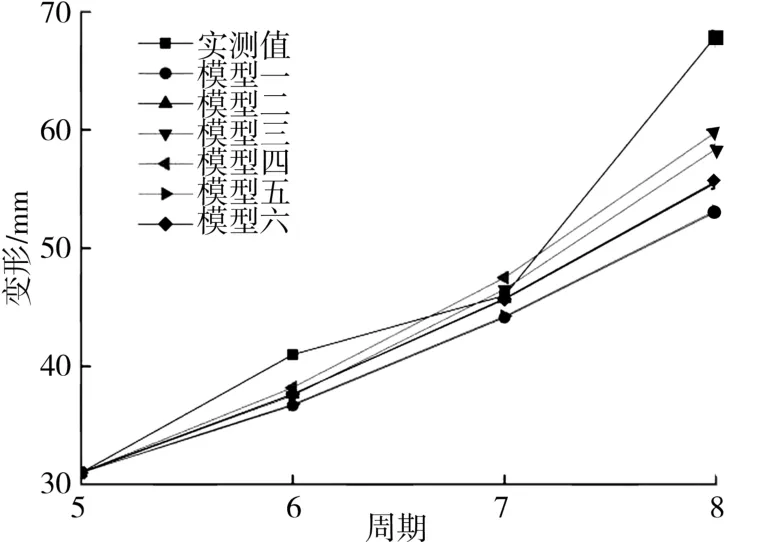
图2 实例一预测值与实测值比较

由图2 可知，对模型进行时间响应函数修正后，其预测曲线更趋近于实测曲线，相对误差更小。 累加预测曲线的绕点旋转在预测值曲线中的表现为预测值向实测值靠拢修正。 分析数据可知，由于前5 期数据增长速率相对缓慢，因此建模拟合函数的预测曲线相对平缓，而以建模序列求解得到的修正角参数实际存在差异，导致修正模型虽然预测精度提高，但是残差依然达到毫米级。 而且第7 期数据出现波动现象，导致旋转后预测残差出现波动，即修正过量的情况，其原因在于修正模型实质依然是以单调凹函数预测后期数据，导致在面对后期出现波动较大的复杂数据时，可能出现修正过量甚至误差增大的情况。

2.2 实例二

选取文献［17］中某施工土石坝观测点9 期观测数据，以前7 期累计沉降作为原始数据序列进行建模、后2 期累计沉降进行预测验证。 分析采用的模型同实例一。

表3 实例二实测建模数据序列值 mm

采用预测相对误差表示模型预测精度，预测结果见表4，模型依然采用C＃程序设计语言实现，如实例一所述。

表4 实例二不同模型预测值与实测值比较分析

根据表4 分别比较模型一和模型二、模型三和模型四、模型五和模型六预测结果，发现对均值GM（1，1）模型、对数变换后均值模型及以x（1）（n）为初始值的均值模型进行时间响应函数修正后的预测精度较原模型均有所提高，说明对模型的时间响应函数进行修正，能使其与实测累加曲线更接近，从而提高预测精度。再比较模型二、模型四、模型六可知，模型二与模型四预测精度相近，而模型六精度较高。

绘制各模型预测曲线与实测曲线对比图（自第7期开始），如图3 所示。

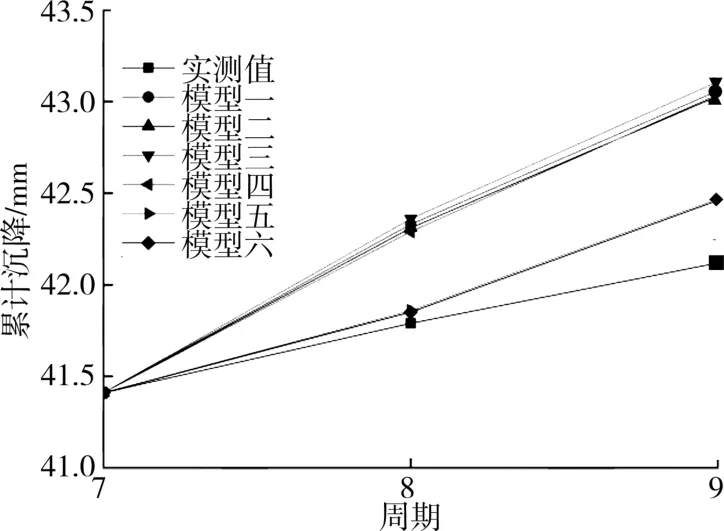
图3 实例二预测值与实测值比较

由图3 可知，实测曲线无明显波动，对模型进行时间响应函数修正后，其预测曲线更趋近于实测曲线。以x（1）（n）为初始值的均值模型预测效果更好，说明该模型所得数据计算求得的修正角参数更接近后期实际。 同时，可以发现实例中后期数据近似线性，而GM（1，1）模型实质为指数函数，模型修正后其凹曲线性质并未改变，短期内预测效果较好，但长期依然会表现出与实测值相离趋势。

2.3 与曲线拟合比较

实例一与实例二均为一元序列，采用回归分析中的曲线拟合进行趋势外推预测较为常见。 因此，采用多项式趋势模型分别对两个实例进行拟合预测，以进行比较分析。 针对实例一采用前5 期拟合函数，后3期对比分析，随着函数指数的增加，得到了指数为1～4的多项式预测结果，其中指数等于1 时为线性预测结果；而实例二采用前7 期拟合函数，后2 期对比分析，随着函数指数增加，得到指数为1 ～6 的多项式预测结果，其中指数等于1 时为线性预测结果。 每个实例各取2 项最好的预测结果与误差较小的改进灰色GM（1，1）模型预测结果进行比较，见表5。

表5 与多项式拟合预测结果比较

根据表5 数据可知，实例一的预测结果中，模型四对于多项式拟合预测具有明显优势，而在实例二的预测结果中，模型六的预测结果与多项式拟合达到的最优预测结果精度相近。 因此，认为修正GM（1，1）模型针对适用的数据序列能够达到较高的预测精度，并且具有一定的稳定性。

2.4 综合分析

对实例一及实例二进行比较分析，发现传统GM（1，1）模型、对数变换后建立的GM（1，1）模型以及以x（1）（n）为初始值的均值GM（1，1）模型针对不同数据的预测精度并不相同。 在实例一中对数变换后建立的GM（1，1）模型较传统模型预测精度高而在实例二中则相反，而比较其后验差比值（C）及小误差概率（P），除了小误差概率（P）均为1 外，后验差比值（C）在两个实例中均表现为对数变换后的模型较传统模型的小，也即对数变换后建模方法更具优势。 分析后验差比值公式可知，其计算仅涉及建模序列，因此应用于预测序列存在不足。 实例一与实例二选取的最佳模型也不同，究其原因有两点：其一是不同建模方法以及不同序列的一次累加序列后期增长率具有差异性，若后期增长率突变则拟合函数拟合效果较好，其预测效果反而可能较差；其二是旋转夹角的取值直接影响后期预测精度，因不同建模方法所得夹角值具有差异性，故预测效果不同。 但是无论传统模型还是改进模型，采用时间响应函数修正的方法进行改进后预测精度均有所提高。

3 结 论

本文针对GM（1，1）模型时间响应函数与实测一次累加序列不完全重合的情况，从一次累加拟合残差修正的角度，提出对单调曲线进行平移旋转以校正一次累加拟合函数，从而使其靠近实测累加曲线，并采用校正后的函数作为新的时间响应函数进行预测，并将此方法推广至改变序列光滑度和初始值等部分的改进GM（1，1）模型。 采用实例对模型算法进行验证，得到以下结论：①对模型进行时间响应函数修正后，其预测精度较改进前提高；②采用后验差比值（C）以及小误差概率（P）进行预测模型选取存在不足；③修正模型依然继承了GM（1，1）模型指数函数的凹曲线特性，因此适用于近似单调递增凹序列，而对于近似线性、凸增长、非单一趋势及预测期突变数据序列，可能出现修正过量或修正较小的情况；④针对预测函数进行变换修正的方法可以向其他以单一趋势为前提的预测方法进行推广。