基于热传递仿真的热电池激活阶段热特性

陈恒帅， 朱艳丽， 李伟， 白杰

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081； 2.北方特种能源集团有限公司西安庆华公司， 陕西 西安 710025)

0 引言

热电池是一种主要用于军事领域的贮备电池，具有可靠性高、激活时间短、工作温度范围宽、耐贮存和可大电流放电等优点[1]。激活过程可描述为：激活信号触发点火头发火，引燃条被点火头点燃，然后引燃条依次将加热片点燃，加热绝缘固态电解质至高导电性熔融态，实现电池内部导通，对外供电。设计合理的烟火系统应具有足够的热量使固态电解质迅速熔化，同时避免温度过高，高温将导致电极材料过多分解，降低容量，甚至引发热失控[2]。

传统的热电池设计工作采取“设计- 验证- 改进”方式进行，随着计算机技术的发展，通过仿真计算可获得热电池内部的温度变化、电压变化等数据，辅助设计工作，显著降低研发周期和成本。热电池激活通过内部热源放热和热量传递实现，基于热仿真技术建立热电池热模型，可计算获得热电池激活阶段温度和相变结果，辅助热电池热设计工作，如用于热电池加热片热值设计[3]和验证热电池设计的效果[4]。对仿真结果进行处理，可实现对热电池激活时间的预测，激活时间的截止时刻需根据假设条件判定。王超等[5]和Li等[6]分别假设电堆中所有隔离片的平均温度和最高温度均达到电解质熔点时刻，热电池激活。可见依据温度结果预测激活时间的假设条件未形成共识。现代化武器快速机动及弹射座椅快速弹射的工作特性，使得在热电池设计阶段，对激活时间预测精度提出更高要求。

在热仿真建模过程中，需要为引燃条和加热片添加符合实际的热源。引燃条和加热片开始放热时刻不同，放热位置也随时间变化。Freitas等[7]和叶丹宏等[8]将热源简化为均一体热源，采用脉冲函数描述热源，脉冲时间等于燃烧时间，脉冲高度为平均热功率。均一热源忽视了热源不同位置放热的时间差，为使模拟结果更精确，Piekos等[9]和Li等[6]分别采用水平集算法和移动网格法表示热源，相比于均一体热源方法，移动热源计算的温度升高更加迅速，不同位置存在温度上升时间延迟，模拟结果更加精确。移动网格虽实现热源放热位置随时间的变化，但未考虑放热反应区，而水平集算法的计算量较大。

针对热电池均一体热源无法精确获得激活阶段温度和电解质相变特性，以及目前以温度结果预测激活时间的方法存在较大的绝对误差，在预测激活时间为几十毫秒的热电池时存在不足，本文采用多物理场耦合分析软件(COMSOL)建立热电池的热模型，并以简便的自定义热源函数描述热电池移动热源。首先分析热电池激活阶段的热特性如温度和相变，通过对热电池激活控制过程固态电解质熔化分析，采用电解质熔化连接正负极时刻作为最短激活时间的截止时刻，克服温度结果预测激活时间的不明确性，实现电池激活时间的精确预测。

1 热传递瞬态效应仿真模型

仿真工作采用COMSOL进行，COMSOL是一款可求解多物理场问题的有限元仿真软件，具有操作界面简洁、定义模型灵活和后处理功能丰富等优点。COMSOL可解决复杂多物理场的传热问题[10]，热电池激活主要是热传递过程，因此仅基于瞬态热传递物理场建立热电池的热模型。前期尝试建立热电池三维模型以体现更丰富的细节，由于计算网格数目过多，导致计算量巨大。尽管利用轴对称性沿对称轴切割，先后建立1/2和1/4中心对称模型，计算量仍然较大。二维模型具有计算时间短和精度高的优点，是目前热电池仿真领域主要采用的建模方法。仿真电池含有14个单体电池，经过预先仿真计算，本文采用COMSOL二维轴对称模型建立热电池二维热模型。

1.1 控制方程

热电池激活阶段涉及热源放热、热传导、对流换热和相变吸热等物理化学过程。此外，热电池导通放电时还存在自发热效应，包含焦耳热、熵减吸热和电极活性材料反应热[11]。本文工作聚焦于激活阶段，自发热效应对整体热量贡献微小，因此未考虑这部分热源。热传递物理场的控制方程如下：

(1)

式中：ρ、Cp和k分别为材料的密度、比热容和热导率；T为温度；t为时间；Qs为加热片和引燃条提供的热量；Qc为空气流过热电池外壳表面发生的对流换热，

Qc=h·(Tf-Tw)

(2)

h为对流换热系数，Tf、Tw分别为空气和热电池表面的温度；Qm为相变材料(隔离片和正极片)中的电解质熔化吸收的热量，

(3)

α为相变材料中电解质的质量分数，ΔHm为单位质量电解质熔化热，θ为电解质的液相体积分数。

1.2 几何模型与网格划分

热电池结构通常由盖体、电堆和壳体组成。盖体由盖板、接线柱、点火头、引出线、石棉垫组成；单体电池、集流片和加热片堆叠并捆扎固定组成电堆；壳体由外壳、保温材料等组成。在热电池加热激活过程中，电堆位置为主要的热释放和传递作用区域。为方便建模和降低计算工作量，建立热电池几何模型时进行适当简化(见图1)。热电池外部为不锈钢外壳，中部为保温层，内部为电堆结构，电堆含有14个单体电池，单体电池及临近部件如图1局部放大部分所示。点火头位于电堆顶部，该热电池用电点火头发火时间相比于激活时间较短，且热量少，对激活时间影响微小，因此建模时未考虑。采用自由三角形网格将几何模型单元化，电堆域的网格大小设为较细化，其余部分设为细化，网格模型如图2所示。

图1 热电池几何模型Fig.1 Geometric model of TB

图2 热电池网格模型Fig.2 Meshmodel of TB

1.3 热源设置

本文以自定义热源函数表示引燃条和加热片热源表达式。以引燃条为例，燃烧示意图如图3所示。图3中，Oxy为平面直角坐标系，引燃条沿x轴正方向以vi匀速燃烧放热，假设y轴方向燃速相等，阴影部分为燃烧反应区，a为反应区宽度。

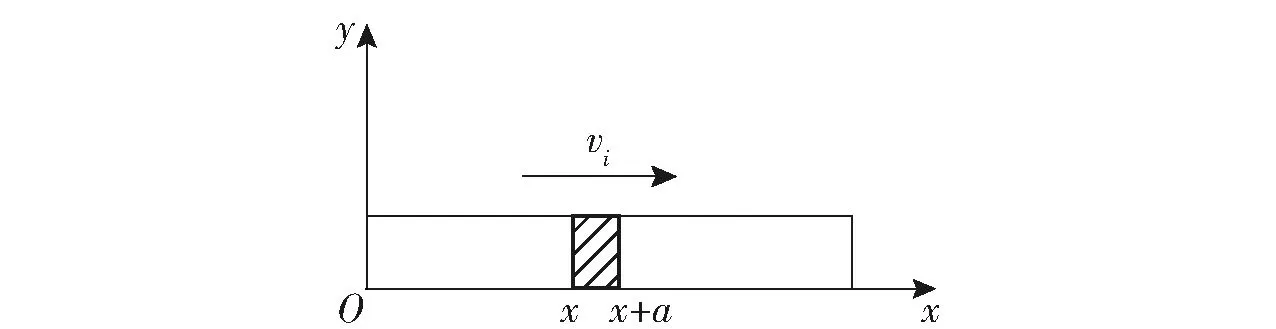
图3 燃烧示意图Fig.3 Schematic diagram of combustion

则引燃条的热功率密度Qi可用横坐标x和时间t的热源函数表达式描述：

(4)

式中：Qv为引燃条热量密度；f(u)为分段函数：

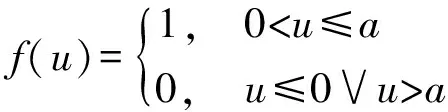
(5)

建模时将引燃条和加热片设为域热源，假定燃烧速度和热量密度恒定，添加计算得到的热源函数。结合实验数据和文献[12]，取加热片燃速为9.10 cm/s，热量密度为1 231.39 J/g，引燃条燃速为167 cm/s，热量密度为1 800 J/g。

1.4 相变域设置

在热电池激活阶段，固相电解质受热将逐渐熔化为液相。电解质主要存在于隔离片中，通常添加MgO作为粘结剂以固定熔融电解质。少量隔离粉添加到正极片中，以起到增大放电表面积、提高传质速率和降低离子浓度极化等作用。当热量传递到隔离片和正极片时，电解质成分将吸热熔化，使正负极导通，激活热电池工作。模拟热电池的电解质为LiCl-KCl，熔点为352 ℃，熔融相变热为244 J/g[13]。设置隔离片域和正极片域为相变域，相变温度为电解质熔化温度，相变热按电解质含量折算。

1.5 热边界条件

热电池的电池壳主要通过热对流方式向环境耗散热量，与电池壳周围的空气在电池壳表面流动有关。建模时将电池壳外界面设为热边界，对流换热系数设置为10 W/(m2·K)，环境温度设为测试实验现场温度。

1.6 材料设置

构建热电池热仿真模型时，需要设置材料的热物理性质参数如密度、热导率和比热容。查阅材料供应商提供的参数，并结合参考文献[4]和文献[14]，获得热电池模型所有部件的材料热物理性质参数。部分材料的热物理性质数据如表1所示。

表1 热电池部分材料热物理性质Tab.1 Thermophysical properties of the partial componentsin TB

2 激活时间验证试验

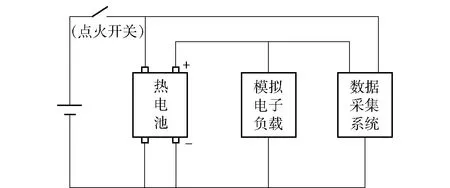
图4 热电池激活测试示意图Fig.4 Schematic diagram of TB activation test

为验证激活时间仿真结果准确性，对热电池进行激活试验。图4所示为试验示意图，采用日本菊水公司PBZ40-10直流电源为热电池输入激活电信号，采用中茂公司63201直流电子负载控制器，维持工作电流为80 mA，采用美国HBM公司GEN3i数据采集系统采集电信号数据。

3 热电池激活特性分析

根据计算结果分析热电池激活特性。基于温度数据绘制电池温度分布图和单体电池温度变化曲线，分析热电池温度特性；基于相变数据绘制电解质相变图，分析电解质熔化相变特性并预测激活时间；基于激活试验的电压曲线，验证激活时间仿真结果；基于引燃条内置式模型的温度和相变结果，分析引燃条位置对激活特性的影响。

3.1 热电池温度研究

图5 部分时刻热电池二维温度分布Fig.5 2D temperature distribution of TB

热电池内部温度数据难以在保持热电池完整性的条件下通过试验获得，而仿真计算可获得电池内部温度分布和变化曲线。图5所示为热电池在40 ms、75 ms和150 ms 3个时刻的二维温度分布。由图5可知：在40 ms时，加热片仍未燃烧完毕，由于引燃条燃速远大于加热片燃速，加热片燃烧锋面几乎在同一直线上；在75 ms时，热电池加热片全部燃烧完毕；在150 ms时，热传递作用使得温度分布比75 ms时刻更均匀，最高温度也由约1 400 ℃降至约900 ℃；在150 ms时间内，电堆端部温度高于其他位置，这与电堆端部额外加热片放热及保温材料延缓热传递有关。多余的热量能够补偿随后放电过程中的向外散热，推迟电堆端部电解质凝固。

3.2 单体电池温度研究

为分析激活过程中单体电池温度变化的特点，在电堆中部的第7组单体电池(由上至下)及临近部件设置域点温度探针，域点探针位置如图6所示。图7为探针温度随时间变化曲线。由图7可知：在40 ms时，加热片燃烧至探针位置，引起温度迅速升高，峰温高达约1 180 ℃；集流片具有相似的温升曲线，峰温约为800 ℃；单体电池部件的探针温度则无类似脉冲变化，表明集流片在激活过程中起到抵御热冲击的作用，缓解电极材料的热分解。隔离片探针温度在电解质熔点352 ℃附近温升速率降低，对应于电解质的相变吸热；正极片存在较少量电解质，对温度曲线影响则不明显；在130 ms时，所有域点温度差小于10 ℃，第7组单体电池及附近部件温度短时维持在560 ℃左右。

图6 域点探针位置(彩色圆点为探针所在位置)Fig.6 Location of domain point probes (The colored dots are where the probes are located)

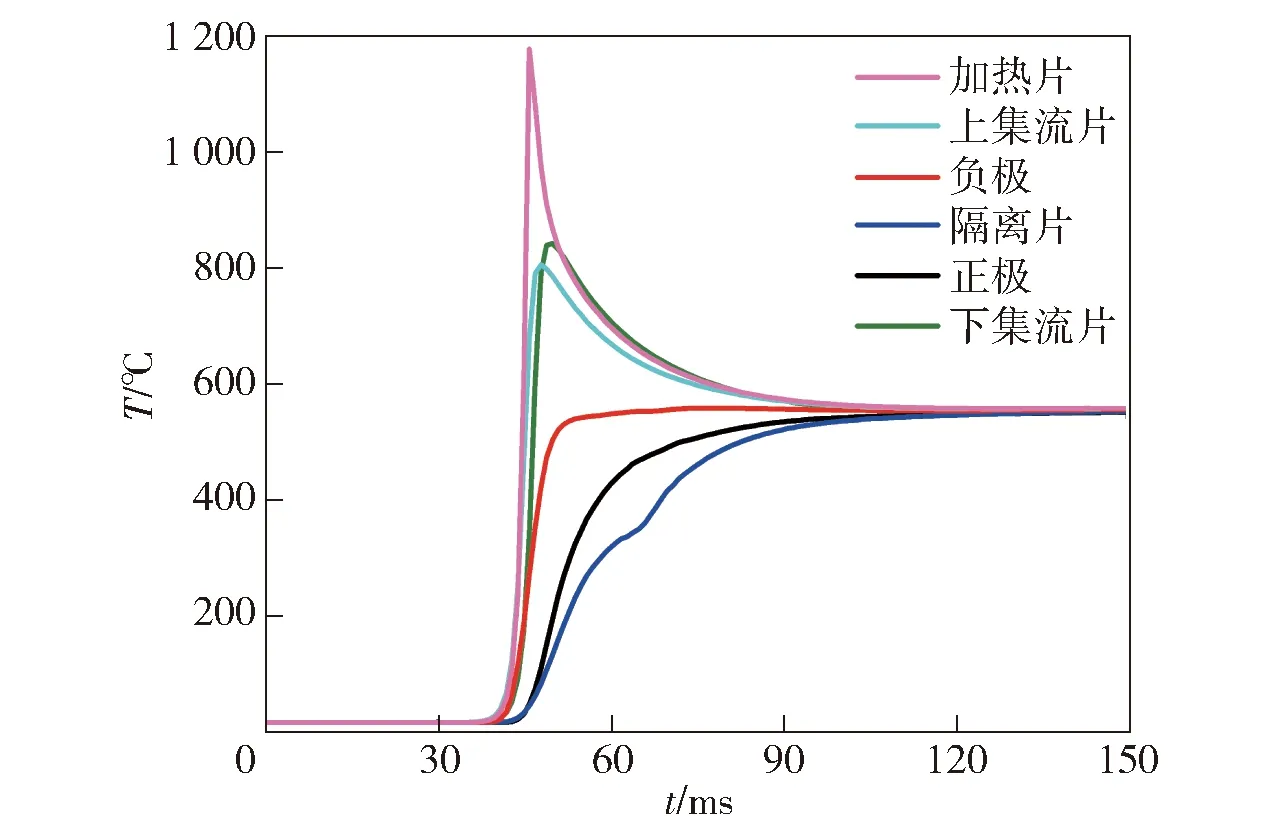
图7 域点探针温度曲线Fig.7 Temperatures curves of domain point probes

3.3 电解质熔化特性

在目前激活仿真研究中，热电池激活时间的截止时刻根据温度假设条件确定：电堆中每个隔离片平均温度或最高温度均达到电解质熔点时，热电池激活。对于激活时间为微秒量级的热电池，该方法预测的激活时间误差较大。隔离片位于正负极之间，温度升高到电解质熔点时，部分熔融电解质可能提前连接正负极，电极材料由于已具有较高温度，电导率和活性得到提升，热电池已经对外放电，从而采用电解质熔化连接正负极时刻作为最短激活时间的截止时刻更准确。电解质熔化状态还可用于分析热电池的带载能力，好于采用开路电压曲线描述的方法[15]。故将电解质完全熔化时刻作为热电池具有完全带载能力的时刻。

图8所示为部分时刻的电解质熔化相变图。由图8可见：正极片由于更接近加热片且电解质含量少，电解质熔化快于隔离片；电解质熔化状态大致呈现上方快于下方、由外向内扩展的趋势，这与加热片由上到下依次被引燃和由外向内逐渐放热有关。由于电堆底部额外加热片和保温层的影响，加快了底部隔离片中电解质的熔化，激活由第13个隔离片熔化状态控制；在45 ms时，每一组单体电池均为导通状态，据此预测热电池激活时间为45 ms；在90 ms时，电解质基本熔化为液相，热电池具备完全带载能力。

图8 部分时刻电解质相变Fig.8 Phase change of electrolyte

3.4 两次激活试验

对热电池进行两次激活测试试验，该热电池的工作电压下限为24 V。热电池激活时间为接收激活信号到放电电压达到24 V经过的时间。测得激活时间分别为42 ms和47 ms，测试结果与仿真值绝对误差为3 ms和2 ms，推测误差与放电测试存在负载、材料性质假设为常数、几何模型与实物存在差异和计算误差等有关。第1次测试的激活信号电压与放电电压曲线如图9所示。从图9中可以看出，初始放电电压升高速率很快，表明激活时电极材料活性已经很高，热电池内部导通瞬间即可对外放电。热电池激活后，放电电压仍存在上升趋势，与电解质进一步熔化、内阻降低有关。

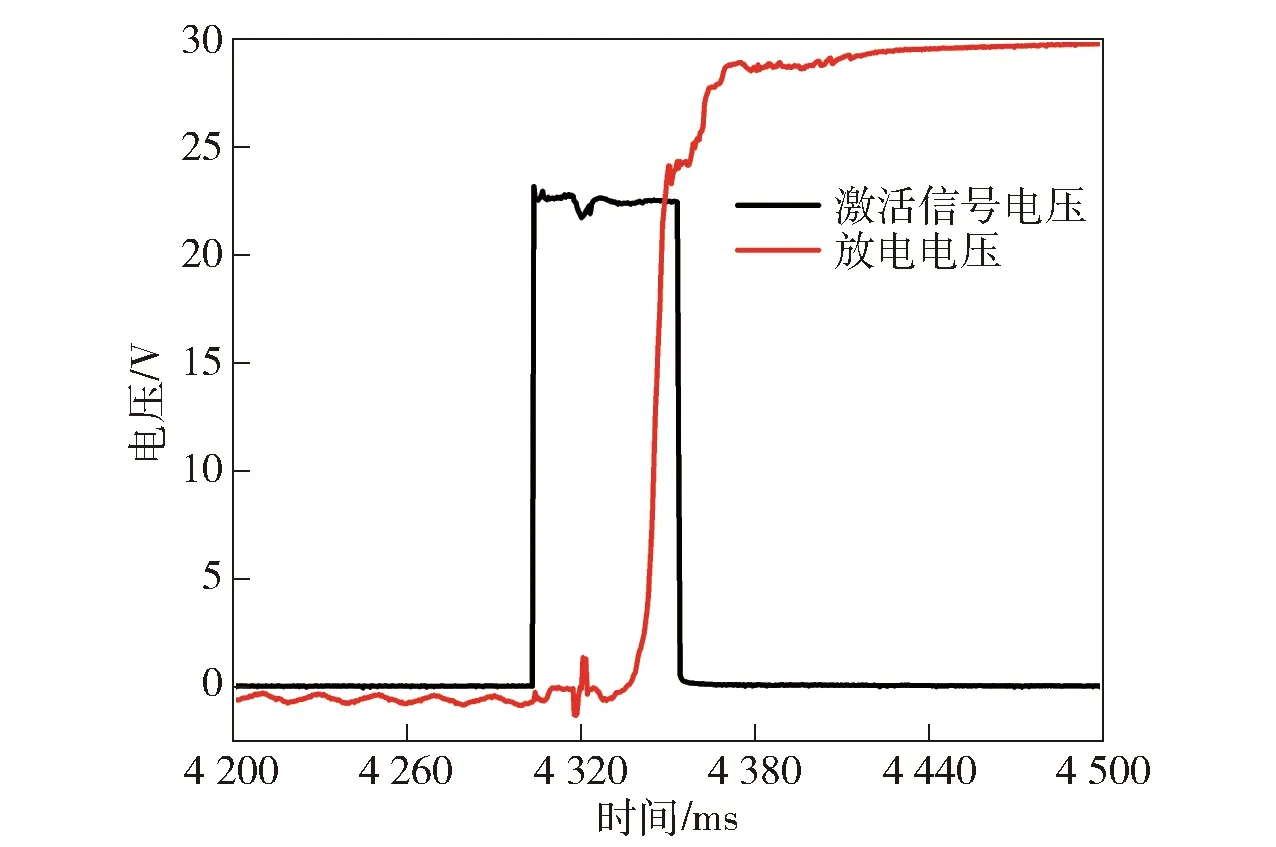
图9 激活信号电压与放电电压曲线Fig.9 Voltage curves of activation signal and discharge

3.5 引燃条放置位置

图10 引燃条内置式热电池部分时刻电解质相变Fig.10 Phase change of electrolyte in the igniting tape built-in TB

根据引燃条放置位置，热电池可分为引燃条内置式热电池和引燃条外置式热电池。为分析两种结构对激活时间的影响，在以上研究基础上建立引燃条内置式热电池模型，建模方法与前文一致。图10所示为内置式热电池在30 ms、45 ms和70 ms时刻的电解质相变图。从图10中可以看出：在30 ms时，热电池内部已经导通，具备放电能力，因此预测激活时间为30 ms；在70 ms时，热电池具备完全带载能力。可见内置式热电池的激活时间和完全带载时间均远低于外置式热电池。原因是去除电堆顶部引燃条，缩短了加热片被引燃时间，加快电解质熔融进程。采用同一位置域点探针对内置式热电池进行温度采集，得到图11所示温度变化曲线。由图11可以看出，单体电池温度短时维持在525 ℃左右，低于内置式的560 ℃，分析原因是建模时两种结构模型的总热量存在一定差异。值得注意的是，两种结构热电池的温度曲线变化几乎一致，表明仿真方法对不同结构热电池具有较好的适用性。

图11 引燃条内置式热电池域点探针温度曲线Fig.11 Temperature curves of domain point probes in the igniting tape built-in TB

4 结论

本文以自定义热源函数描述引燃条和加热片的移动热源，通过瞬态计算获得热电池激活过程中的温度和电解质相变结果，分析了热电池整体和单体电池的温度特性，根据电解质熔化状态预测了激活时间。进行热电池激活试验，对激活时间预测值进行验证。此外研究了引燃条放置位置对激活时间的影响。得出以下主要结论：

1)电堆端部温度较高，可以补偿放电过程中的散热，推迟端部电解质凝固，延长工作寿命。集流片在激活阶段具有抵御热冲击作用，有效降低单体电池峰温，缓解电极材料热分解。

2)热电池激活试验测得的激活时间与预测值接近，预测值为45 ms，实测值为42 ms和47 ms。

3)内置式引燃条结构相比于外置式，由于引燃条传火路径变短，能够显著缩短激活时间，预测激活时间为30 ms。