小尺寸低质量比的并联圆柱涡激振动仿真研究*

赵 鹏 王晓凯 张 耀

(1.中国海洋石油国际有限公司 2.海洋石油工程(青岛)有限公司)

0 引 言

石油是国家经济发展不可或缺的一种重要战略资源，随着社会生产力的飞速发展，陆地油气资源日渐短缺。海洋面积广阔，油气资源潜力明显，目前海洋油气勘探开发已成为全球石油行业的主战场[1-2]。立管在海洋油气开发中扮演着极为关键的角色，是连接海面平台与钻采设备之间的重要枢纽。

当海流以一定的速度流经立管时，受立管内部高温、高压输送介质与外部海洋环境载荷的共同作用，立管容易出现涡激振动现象[3-5]。在涡激振动的长期作用下，立管不仅会产生疲劳损伤，造成使用寿命大幅缩短，而且会引发事故甚至带来巨大的经济损失，并对生态环境产生严重破坏[6-8]。因此对于立管涡激振动的相关问题必须引起重视。

CUI Z.D.等[9]采用有限元模拟法，通过求解N-S方程对并联排列的弹性耦合圆柱体涡激振动展开研究，其中当雷诺数Re=5 000、质量比m*=2时，研究发现两个柱面的主响应频率在“锁定”状态内外始终保持一致。宋振华等[10]对不同质量比下的圆柱模型进行了双自由度模拟研究，发现顺流向振动的存在会导致横流向最大振幅显著增大。M.RAHMANIAN等[11]对两个不同直径并联排列圆柱体的涡激振动进行了研究，两圆柱仅考虑横流向振动，结果表明，小圆柱体的存在对大圆柱体的漩涡脱落方式和振动幅值会产生较大影响。王晓凯等[12]针对串联双圆柱进行了二维仿真研究，结果表明，在串联两圆柱间距比为4的工况下，上游圆柱对下游圆柱的尾流干涉作用相对较弱。宋振华等[13]通过附属杆抑制装置对海洋立管模型的涡激振动抑制进行了深入研究，结果表明，附属杆对立管的泄涡有较好的抑制效果，此外，抑制效果受间距比和来流角度的影响较大。刘志慧等[14]使用盘球附体这一新颖的抑振装置开展了海洋立管的涡激振动模型试验，对于有效提升盘球附体的抑振效果提供了重要的参考意见。娄敏等[15]采用仙人掌形截面对圆柱模型进行涡激振动抑振试验研究，并通过数值模拟进行了对比验证，结果表明，仙人掌形截面能够对圆柱体的振动产生明显的抑制效果。冯丽苹等[16]在均匀流条件下对并联布置的5根立管模型开展试验研究，重点关注了立管群的无量纲振幅、质心运动轨迹和漩涡脱落频率等动力响应，分析了并联立管在干涉作用下的涡激振动规律。

传统的涡激振动理论和分析模型主要建立在单一圆柱体研究基础上，涉及流动干涉作用下小尺寸低质量比圆柱的研究相对较少，有待进一步补充完善。立管在室内波流水槽中的涡激振动模型试验通常使用有机玻璃材质(Polymethyl methacrylate，PMMA)的圆柱，它的综合力学性能较好、机械强度较高，外径在20 mm左右，同时质量比偏低，便于开展试验，因此试验模型常被称为小尺寸低质量比圆柱。

本文基于Overset-Mesh技术[12]对流场区域进行网格划分，将振动模型简化为双自由度质量-弹簧-阻尼系统，将包含DEFINECGMOTION宏命令的自定义函数编译到Fluent软件中，结合动网格技术建立二维流固耦合数值模型，对小尺寸低质量比并联双圆柱的涡激振动幅值响应、受力特性以及运动轨迹进行仿真研究。

1 理论方法

1.1 基本方程

CFD(计算流体动力学)方法首先从基本方程入手，三大基本控制方程是CFD的核心组成部分，由于本文中涉及的研究对象不存在能量的转化过程，所以仅需考虑质量和动量两个守恒方程。

1.1.1 连续性方程

连续性方程也称做质量守恒方程，适用于所有的流体运动问题。连续性方程微分形式为：

(1)

式中：u、v、w分别为速度矢量在x、y、z方向上的分量，m/s。

1.1.2 动量方程

动量方程是符合牛顿第二定律要求的数学表达式，即动量Navier-Stokes方程：

(2)

式中：i，j=1，2，3；ui、uj表示在i方向及j方向上的速度分量，m/s；Si表示在i方向上的源项；t表示时间，s;p表示流场压力，Pa。

1.1.3 控制方程

不可压缩黏性牛顿流体的控制方程为：

∇·u=0

(3)

(4)

式中：∇表示梯度算子；Re为雷诺数，无量纲。

1.2 流固耦合

海洋立管在来流作用下产生的涡激振动现象是典型的流固耦合问题，分析此类问题时通常需要使用动网格技术。求解器根据在每个迭代步中边界的变化情况自动完成网格的更新过程，在更新时保证网格的拓扑结构始终保持不变。同时，流体域中不会因网格运动而产生流体速度，而结构域中网格运动速度与结构运动速度始终保持一致。

本文采用Fluent流体软件对圆柱运动和周围流场变化进行分析，通过函数UDF(User Defined Functions)中的DEFINECGMOTION宏命令实现网格的更新，同时利用Fluent中的内部函数提取出流体施加给圆柱的流体力并传递给运动控制方程，通过计算得到运动边界的速度。涡激振动求解流程如图1所示。

图1 涡激振动求解流程Fig.1 Solution process of vortex-induced vibration

1.3 相关参数

涡激振动是一种流场和结构相互作用的耦合现象，在涡激振动的研究中涉及到多个无量纲参数，这些参数对于流体力学中的诸多实际问题具有重要意义。

1.3.1 雷诺数

雷诺数Re为黏性流体在运动时惯性力与黏性力相对大小的无因次数，是流体力学研究中影响最为广泛的无量纲参数之一。其计算式为：

(5)

式中：U表示来流速度，m/s；D表示圆柱外径，m；υ表示流体的运动黏性系数，m2/s。

1.3.2 斯特劳哈尔数

斯特劳哈尔数St通常由试验测得，是与漩涡脱落频率相关的无因次量。其计算式为：

(6)

式中：fs表示漩涡脱落频率，Hz。

1.3.3 约化速度

约化速度Vr是用于表述来流速度和圆柱结构自振频率间相互关系的一个无量纲参数，在涡激振动的特性研究中，经常用约化速度代替来流速度。相关计算式为：

(7)

式中：fn表示圆柱体固有频率，Hz。

1.3.4 频率比

频率比f*为涡激振动的响应频率与圆柱结构的固有频率之间的比值。其相关计算式为：

(8)

式中：fs表示结构响应频率，Hz。

1.3.5 质量比

质量比m*为单位长度的圆柱结构质量m与其排开相同体积的流体质量的比值。其计算式为：

(9)

式中：ρ为流体密度，kg/m3。

1.3.6 间距比

间距比S/D表示两个圆柱中心连线之间的距离S与圆柱外径D的比值，如图2所示。

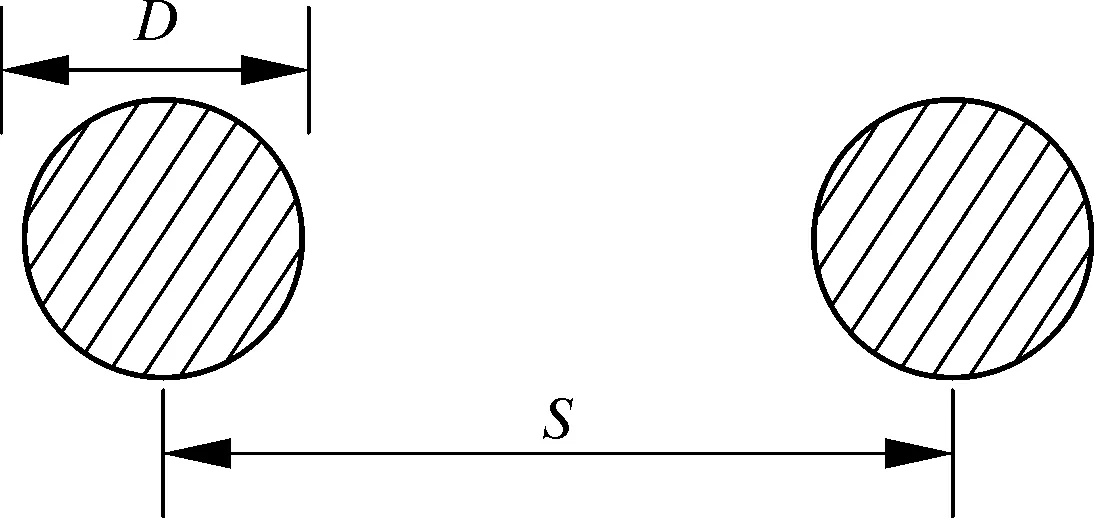
图2 间距比Fig.2 Spacing ratio

2 数值模型

2.1 模型参数

本文数值模拟中所采用圆柱模型的基本参数为：圆柱外径D=0.02 m，质量比m*=2.55，阻尼比ξ=0.003，固有频率fn=1.72 Hz。

根据T.K.PRASANTH等[17]对网格尺寸的研究结果，流场区域在能够满足尾流区长度和整体高度的要求时，圆柱结构的涡激振动响应将会避免边界效应的影响。因此，为提升数值模拟结果的准确性，将流场区域适当增大，设定为40D×20D，同时基于Gambit软件与Overset-Mesh技术[12]进行前处理网格划分，流场区域计算模型如图3所示。圆柱外径D=0.02 m，两圆柱为等径并列布置，圆柱间距比S/D分别设置为3、4和5。

来流速度对于涡激振动有重要的影响，本文选取的流速范围为0.034 m/s≤U≤0.516 m/s，由公式(7)可得约化速度为1≤Vr≤15；同理根据式(5)得到雷诺数范围为680≤Re≤10 320，属于亚临界区域。

图3 计算模型网格划分Fig.3 Mesh division of computational model

2.2 模型验证

为验证所建立计算模型与前处理过程的可靠性，在雷诺数Re=200时进行圆柱绕流数值模拟。根据式(5)，来流速度为0.01 m/s。圆柱绕流模拟结果如图4所示。

2.2.1 升力和阻力系数分析

实际研究中，漩涡泄放脱落使圆柱产生周期性的升力Fl和阻力Fd往往利用升力系数Cl与阻力系数Cd来表示，升力和阻力系数随时间历程的变化曲线如图4a所示。从图4a可知，当流动持续一定时间后升力和阻力系数将趋于稳定。

2.2.2 频率分析

漩涡脱落的频率与升力系数的变化周期直接相关，通常采用功率谱密度(Power Spectral Density)来描述随机信号的频域特征。图4b为雷诺数Re=200时的升力和阻力系数所对应的功率谱密度图。

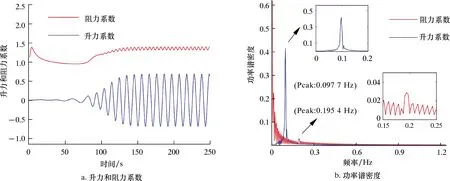
图4 圆柱绕流模拟结果Fig.4 Simulation results of flow around cylinder

由图4b可得，圆柱横流向振动的主频率约为0.097 7 Hz，顺流向振动的主频率约为0.195 4 Hz，顺流向的数值为横流向的2倍，符合阻力周期是升力2倍的相关规律。同时由式(6)得到斯特劳哈尔数St≈0.195，根据圆柱绕流在亚临界区域内的特性，在此雷诺数范围内斯特劳哈尔数St数值在0.2左右，因此可以判断计算结果较为准确。

2.2.3 结果对比

将模拟得到的圆柱绕流结果与文献[18-21]的研究结果进行对比，结果如表1所示。由表1可知，本文圆柱绕流模拟得到的升力系数、阻力系数和斯特劳哈尔数与相关各文献中的参考值均较为接近，从而确保了所选取的网格划分方法、数值求解格式等参数的可靠性。在以下的数值模拟中可以使用该模型进一步开展流固耦合的计算分析。

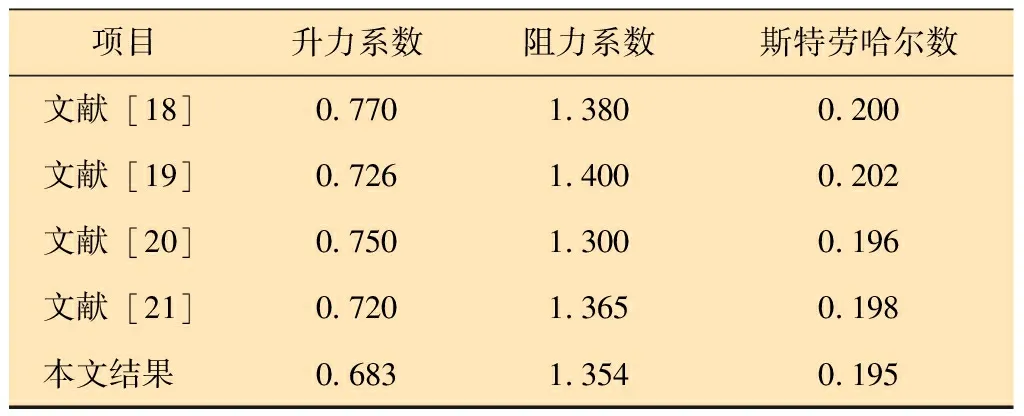
表1 圆柱绕流结果对比Table 1 Comparison of flow around cylinder

3 计算结果

当两个圆柱体的中心连线与来流方向垂直时，则将这种排列方式称为并联排列。图5为双圆柱并联排列示意图。顺着来流方向对两圆柱进行命名，将来流方向左侧的称为左侧圆柱，右侧的称为右侧圆柱。

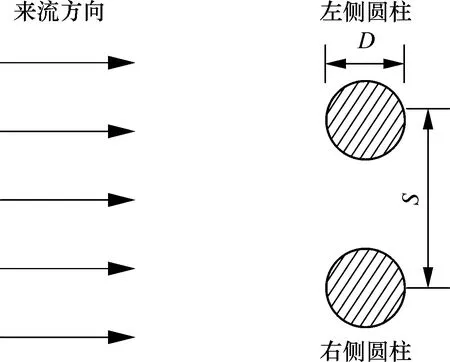
图5 双圆柱并联排列示意图Fig.5 Schematic diagram of two side-by-side cylinder

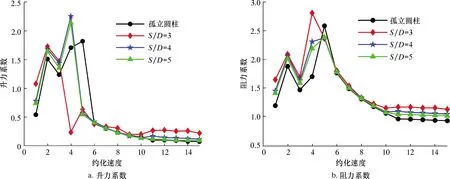
图7 不同间距比下圆柱升力系数和阻力系数变化特性Fig.7 Lift / drag coefficients of cylinder at different spacing ratios

3.1 圆柱漩涡脱落频率

“锁定”现象是涡激振动问题的显著特征，当漩涡脱落频率fs在数值上十分接近固有频率fn时，频率比fs/fn趋于稳定且不再随约化速度的增大而相应增加，此时可认为圆柱出现“锁定”现象。图6为不同工况下圆柱频率比随约化速度的变化关系。从图6可以看出，随着Vr的不断增大，频率比在数值上相应增加，随后在某一区间内频率比的数值趋于稳定，符合“锁定”区域的相关特征。因此，孤立圆柱的“锁定”区间为Vr=6～10；当S/D=3时，并联两圆柱的“锁定”区间为Vr=4～9；当S/D=4时，“锁定”区间为Vr=5～9；当S/D=5时，“锁定”区间为Vr=5～10。受两圆柱相互干涉作用的影响，并联圆柱的频率比与孤立圆柱相比存在明显差异，同时间距比的增大会导致并联圆柱“锁定”区间随之变宽。

图6 不同间距比下圆柱频率比Fig.6 Frequency ratios of cylinder at different spacing ratios

3.2 圆柱受力特性

图7为圆柱升力系数和阻力系数变化特性。从图7可见：圆柱的阻力系数与升力系数随约化速度的变化过程总体相似，表现为先增后减的两段式进程；在低约化速度范围内，阻力系数与升力系数呈增大趋势；进入“锁定”区间后，升力系数和阻力系数持续下降并逐渐趋于稳定。

同一间距比下并联两圆柱的受力情况基本一致，不会随间距比的增大受到较大影响，在进入高约化速度后趋于稳定，随着间距比增大，升力系数和阻力系数呈现下降趋势。

3.3 圆柱相对幅值

约化速度对涡激振动的响应幅值会产生一定的影响，本文研究中采用相对幅值(系统振动时圆柱体在不同流向处的振幅值与其直径之比值)来具体表征。

图8为圆柱在不同约化速度下的相对幅值变化曲线。由图8a可得：横流向相对幅值随约化速度的变化呈先增大、再平稳到最后下降的三段变化趋势；孤立圆柱在Vr≤5时，圆柱的涡激振动现象随着来流速度的增加由弱到强，在Vr=5处横流向振幅达到最大值0.688D；当进入“锁定”区间内，漩涡泄放脱落过程更加明显，漩涡之间相互融合使得漩涡强度得到提升，从而在流体与圆柱之间产生了剧烈的非线性动力相互作用，致使圆柱结构能够持续较大幅度的振动，大致在0.44D；在Vr>10后圆柱脱离“锁定”区间，横流向相对幅值开始减小并逐渐稳定在0.014D附近；受两圆柱相互间的干涉作用影响，并联圆柱的相对幅值最大值接近0.46D，小于孤立圆柱时的峰值，进入“锁定”区间后，横流向相对幅值趋于稳定保持在0.4D附近。在高约化速度范围内并联圆柱的相对幅值将大于孤立圆柱，而在“锁定”区间内时则小于孤立圆柱，同时间距比的增大会导致并联圆柱横流向相对幅值减小。

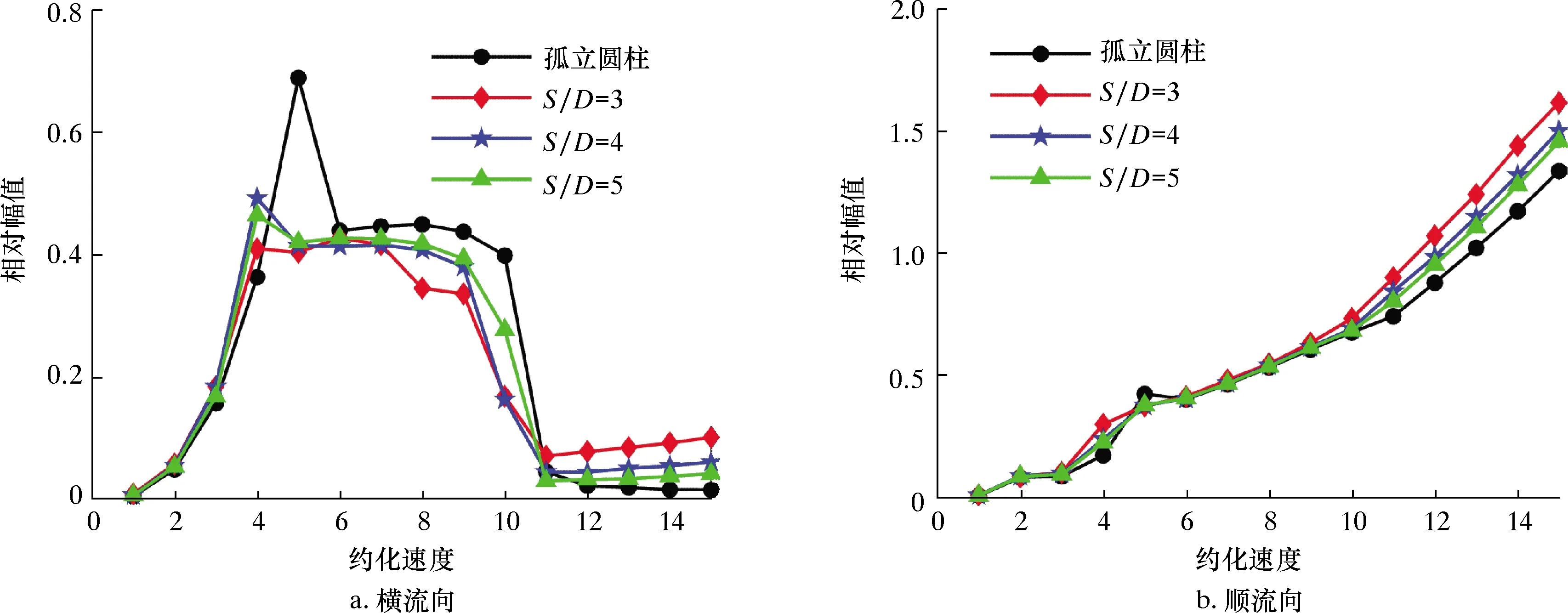
图8 不同间距比下圆柱相对幅值变化曲线Fig.8 Relative amplitudes of cylinder at different spacing ratios

从图8b可见，圆柱顺流向的相对幅值随着约化速度的增加呈现持续增大的趋势。这是由于随着Vr增大，流经圆柱结构的来流速度相应提升，圆柱在顺流向方向上受到的冲击作用越来越强，圆柱顺流向振动的中心点距离原点越来越远，因此在顺流向的相对幅值持续增大。当间距比逐渐增大时，并联圆柱顺流向相对幅值相应减小，与孤立圆柱的曲线重合度也将不断提高。由此可得并联圆柱间的流动干涉作用强度与间距比大小成反比关系，当间距比增大到某一值时，并联两圆柱的振动将无限接近孤立圆柱时的情况，此时左侧圆柱与右侧圆柱间的流动干涉作用可以忽略不计，视为两个孤立存在的圆柱。

3.4 圆柱质心运动轨迹

提取孤立圆柱质心运动轨迹，其随约化速度的变化关系如图9所示。从图9可见：在流体力耦合作用的影响下，运动轨迹主要以“8”字形为主，在进入“锁定”区间后运动轨迹趋于稳定，“8”字形大小基本保持不变；随着约化速度继续增大，离开“锁定”区间后，横流向振幅迅速减小，由于存在强烈的多频振动拍现象，导致“8”字形轨迹呈现出散乱的形态；同时，“8”字形的偏向发生改变，说明此时在两个流向上的振动相位出现偏差，即发生“相位开关”现象。因此，约化速度对于圆柱运动轨迹有显著影响。

图10表示在不同间距比时并联圆柱的质心运动轨迹随约化速度的变化情况。并联圆柱的排列方式决定了两个圆柱的运动轨迹存在对称相似性。并联圆柱的运动轨迹形态构成相对简单，常见的运动轨迹主要包括“8”字形、“桃”形和“水滴”形等。

图9 孤立圆柱的运动轨迹Fig.9 Motion trajectories of isolated cylinder

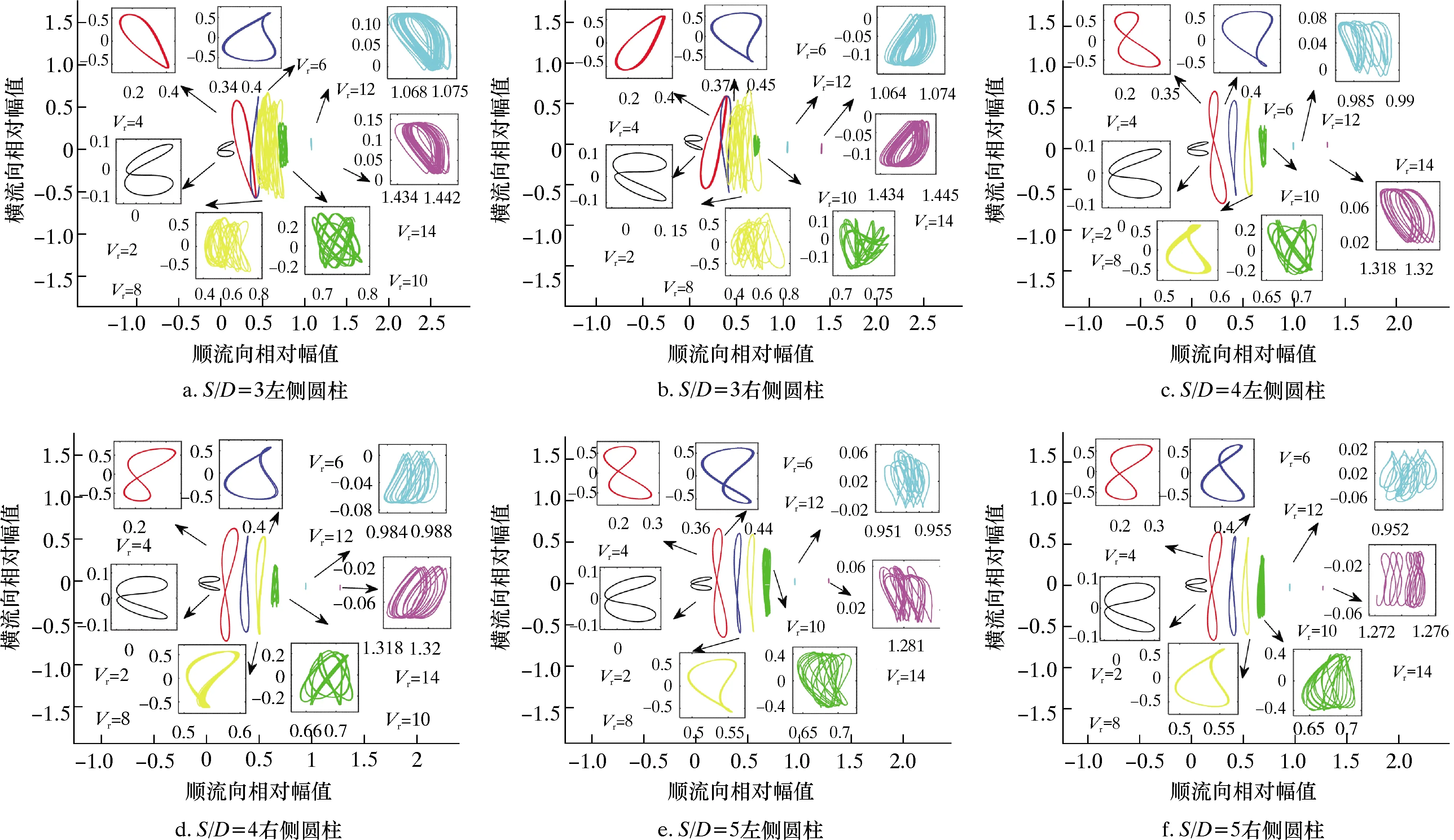
图10 不同间距比下圆柱运动轨迹Fig.10 Motion trajectories of cylinder at different spacing ratios

当间距比S/D=3时，“8”字形轨迹出现频率较低。从图10a可见，当Vr=2时，黑色“8”字形与孤立圆柱相比对称性较差、整体形状并不标准。随着间距比的增大，“8”字形轨迹的出现频率越来越高，同时上下两部分逐渐趋于对称形态且愈发标准。进入高约化速度范围后，圆柱运动的非周期性得到加强，与孤立圆柱时的情况类似，存在强烈的多频振动拍现象，此时运动轨迹出现重合。总之，并联圆柱的运动轨迹受间距比的影响较小，随着间距比的增大，并联两圆柱的质心运动轨迹愈发接近于孤立圆柱，从侧面体现出两圆柱间的流动干涉作用在逐步减弱。

4 结论及建议

本文采用CFD数值模拟方法对并联两圆柱的涡激振动问题进行了研究，主要得出以下结论。

(1)孤立圆柱的“锁定”区间为Vr=6～10，处于“锁定”区间时频率比保持在1附近，横流向相对幅值显著增大，升力系数和阻力系数持续下降并逐渐趋于稳定。

(2)圆柱运动轨迹主要以“8”字形为主，离开“锁定”区间后横流向振幅迅速减小，多频振动拍现象强烈，导致“8”字形轨迹形态散乱，同时“8”字形的偏向逐渐转变，即发生“相位开关”现象。

(3)并联布置的排列方式导致两圆柱在升力系数、阻力系数、相对幅值和运动轨迹等方面极为相似，受彼此干涉作用的影响，振动特性与孤立圆柱相比存在一定差异。

(4)并联两圆柱间的流动干涉作用强度与间距比的大小成反比，当间距比增大到某一值时，左侧圆柱与右侧圆柱间的干涉作用可以忽略不计，两圆柱的振动将无限接近孤立圆柱时的情况。

(5)海洋平台立管群的布局应考虑适当增大立管在垂直于来流方向上的距离，以此减少立管群之间流动干涉作用的影响，从而降低立管发生疲劳失效的概率，并延长其使用寿命。

(6)本文的研究仍存在一定的局限性，结合在研究过程中所遇到的问题同时考虑工程实际情况，对今后的研究主要从以下两个方面提出建议：①应进一步对交错圆柱(来流方向不垂直于2个圆柱体的中心连线)以及3个或3个以上圆柱体并联等情况下的涡激振动响应特性进行研究；②对于海洋立管流动干涉作用下振动机理的认识相对有限，建议今后从理论层面着手，对立管间的流动干涉作用进行充分完整的分析。