无人机骑手联合外卖配送路径优化问题研究

赵强柱，卢福强，王雷震，王素欣

1.东北大学 信息科学与工程学院，沈阳 110004

2.东北大学秦皇岛分校，河北 秦皇岛 066004

3.燕山大学 经济管理学院，河北 秦皇岛 066004

近年来，随着移动互联网的普及和餐饮O2O的快速发展，陆续出现了饿了么、美团外卖等第三方外卖平台，外卖点餐早已成为有别于传统堂食的另一种餐饮消费模式[1-2]。外卖配送作为外卖业务从线上到线下的关键环节，配送路径的规划不仅直接决定餐品的准时送达与否，而且对商家的外卖运作成本和利润有着重要影响[3]。骑手送餐是现阶段主要的外卖送餐方式，骑手通过骑摩托车或电动车将餐品送到消费者手中，但这种方式存在很多弊端：在交通高峰期，城市道路拥堵，导致送餐到达时间延误，顾客满意度降低；骑手配送服务范围有限，对稍远顾客的订单不能够及时送达，或因超出骑手配送范围，商家不得不拒绝接受此类订单，导致顾客数量减少[4-5]。因此，如何提高餐品准时送达率，减少配送成本，是外卖行业亟待解决的问题。

为适应行业发展，饿了么、美团等外卖平台开始逐渐将无人机应用于外卖配送领域中，使无人机与骑手共同完成配送任务。2018年5月29日，饿了么宣布获准开通中国第一批无人机即时送餐航线，并在上海举行无人机商业飞行发布会[6]，送餐无人机正式投入商业运营。目前饿了么投入使用的无人机最高飞行速度为65 km/h，最大载重可达10 kg，满载续航距离最远为20 km。配送过程中，无人机主要承担集散点A到B的干线运输，两名骑手则分别负责将外卖餐品装运上飞机和将餐品送达消费者手中。因此，无人机骑手联合外卖配送的路径优化问题研究具有非常现实的研究背景和十分重要的研究意义。

目前，虽然没有对无人机骑手联合外卖配送的模式的研究，但国内外学者对外卖配送路径优化问题的研究不少。翟劲松等[7]在单配送中心情景中以总行驶时间最小为目标进行带有硬时间窗的外卖配送研究；Liao等[8]研究了一种将外卖配送与车辆路径问题相结合的绿色配送路径问题，提出了以最大顾客满意度、最优骑手平衡利用率、最少碳排放为目标的多目标绿色配送路径模型；Naccache等[9]构建了考虑时间窗的多个取送货点车辆路径问题模型，分别使用改进的自适应大邻域搜索算法（ALNS）与精确算法分支定界法对算例求解；Ulmer等[10]考虑顾客下单时间的不确定性和餐品出餐时间的不确定性，研究随机动态取送货问题；陈萍等[11]以时间满意度为目标，考虑外卖的取送货次序约束，并据此设计遗传算法，最终实验得出统一取货再集中配送的优化结果；李桃迎等[12]以外卖配送成本增量总和为目标，以聚类为手段，将多配送员外卖配送问题转化为单配送员问题，并依托遗传算法实现问题求解；张力娅等[13]基于O2O外卖平台的配送现状分析，引入外卖平台顾客优先级概念，从顾客满意度和配送成本两个角度出发，建立了考虑客户优先级的、带时间窗的、动态的、多车场多目标取送货车辆路径模型，采用加权法将多目标转化成单目标，并设计改进的迭代局部搜索算法对模型进行求解。

综上，虽然现有文献对外卖配送路径优化问题从不同的考虑因素上均有研究，但这些文献的研究背景都是仅骑手配送的单一配送模式。结合实际商业案例，考虑到国内外卖的应用场景和城市建筑物密集复杂、不具备无人机入户定点投放等特点，本文以最小化送餐成本为目标建立了无人机骑手联合外卖配送的路径优化模型，并设计了一种引入时空距离的两阶段启发式算法进行求解。在第一阶段，基于时空距离的度量，运用结合K-means算法的遗传算法对顾客聚类，得到骑手的初始路径；第二阶段，以最小送餐成本为目标对骑手送餐路径和无人机送餐航迹优化。

1 问题描述及假设

传统的仅骑手外卖配送模式如图1（a）所示，骑手在商家取餐后直接送至顾客手中。在送餐时，由于骑手往往凭借经验对顾客逐个配送，通常不能实现最短路径的配送方案；另一方面，骑手在凭借经验规划路径时大多只考虑了顾客的地理位置，而忽略了订单的下单时间，产生的配送方案有可能对时间窗宽松、距离商家较近的顾客先行配送，而对时间窗紧迫、距离商家较远的顾客稍后配送进而导致餐品不能准时送达。

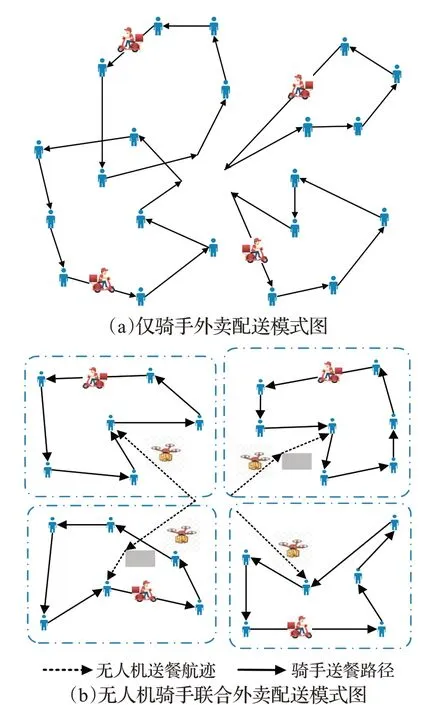
图1 仅骑手配送模式和无人机骑手联合送餐模式图Fig.1 Schematic diagram of riders only delivery mode and drones and riders joint delivery mode

本文研究的无人机骑手联合外卖配送如图1（b）所示，商家在某一时段接收顾客订单，出餐后统一将多份餐品送至无人机上，无人机避开障碍物将餐品送至某个顾客点附近（无人机降落点），骑手取出餐品后按照预先规划好的路径将餐品送至各个顾客手中。

根据无人机骑手联合外卖配送的实际案例，本文做出如下假设：

（1）由于电动车行驶距离约为50 km，远大于一次送餐的行驶距离，故不考虑电动车的续航问题。

（2）由于无人机满载续航约为20 km，足够飞行往返完成一次送餐任务，故不考虑无人机的续航问题。

（3）无人机的飞行速度、电动车的行驶速度恒定。

（4）将每份餐品的质量与体积视为单位固定值。

（5）对每个顾客的送餐服务时间视为固定值。

（6）在骑手在送餐过程中，不考虑天气时况、交通状况或其他意外事件。

（7）送餐电动车和无人机均有容量限制，且无人机最大容量等于电动车最大容量。

2 模型构建

符号定义如下：

K={k1,k2,…,k m}：骑手所驾驶的电动车的集合；

V={v0,v1,…,v n}：商家与顾客的集合，其中v0表示商家，v1,v2,…,v n表示n个顾客；

G={g1,g2,…,g m}：无人机停靠点集合，G⊆V；

t i：骑手骑行电动车到达顾客i时的时间；

t s：对每个顾客的送餐服务时间；

d ij：顾客i与顾客j之间的空间距离；

s：骑手所驾驶电动车的平均速度；

t ijk：表示骑手k从顾客点i到顾客点j之间所用时间；

qi：顾客i下单的外卖量；

[0,T i]：顾客i的时间窗，T i表示顾客i的预期送达时间；

Q：单个送餐无人机的最大装载量；

a：骑手所驾驶电动车的单位距离运输成本；

b：无人机送餐时的单位距离运输成本；

xijk：决策变量，若骑手k从顾客点i到顾客点j时为1，否则为0。

本文以最小化送餐成本作为目标函数建立模型，送餐成本包括三部分，即电动车运输成本、无人机运输成本以及惩罚成本。其中惩罚成本P i表示如下：

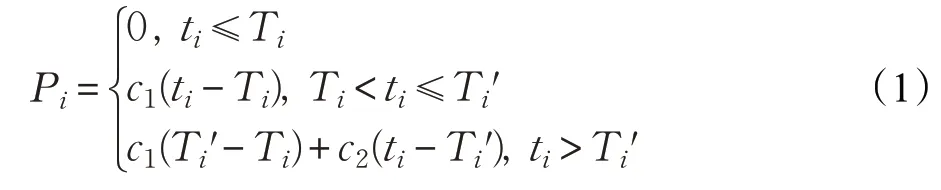
本文采用分阶段惩罚函数来刻画惩罚成本。当骑手在顾客i的时间窗内到达顾客i时，即t i≤T i时，无惩罚成本；当骑手超过预期送达时间到达顾客i时，顾客的满意度会下降，因此出现了惩罚成本，c1为此阶段的单位时间惩罚成本；设定一个最迟送达时间T i′，令T i′＞T i，当到达时间超过最迟送达时间Ti′，顾客满意度会急剧下降，惩罚成本急剧增加，c2为此阶段的单位时间惩罚成本，c2＞c1＞0。外卖送达时间t i与惩罚成本Pi关系如图2所示。

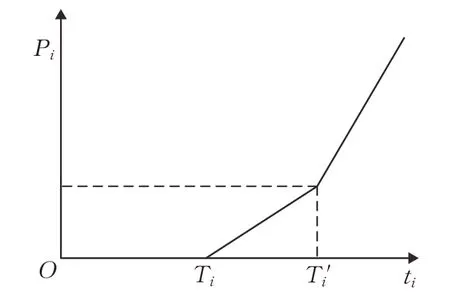
图2 惩罚成本函数Fig.2 Punishment cost function

最小化送餐成本的目标函数如式（2），等式右边三项分别为送餐时电动车的运输成本、无人机运输成本和惩罚成本。

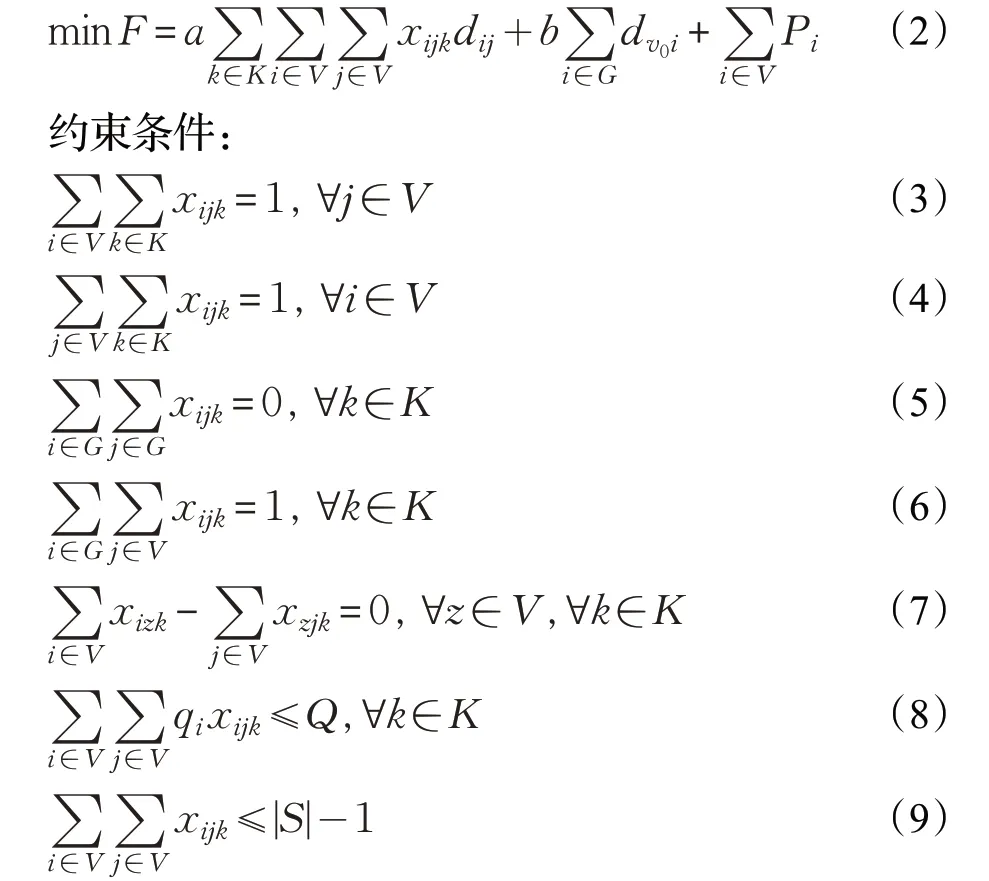
式（3）和式（4）共同表示一个顾客只能由一个骑手进行一次送餐服务；式（5）表示骑手不能由无人机停靠点直接开往另一个无人机停靠点；式（6）表示所有的骑手必须从无人机停靠点出发；式（7）确保骑手在起始点和结束点之间的路径是连续的：式（8）表示送餐时的载货量约束；式（9）为简单圈约束，消除路径中的子回路。将约束（6）改写为表示骑手须从商家出发最终回到商家，上述模型即为仅骑手配送模式下的骑手路径模型。

3 两阶段启发式算法设计

针对无人机骑手联合外卖配送场景下的路径优化问题，本文设计了一种两阶段启发式算法进行求解。第一阶段构造骑手初始路径，先对顾客点基于时空距离进行度量，在此基础上采用结合K-means算法的遗传算法对顾客订单聚类，根据时空距离远近构造骑手初始路径。第二阶段路优化骑手路径和无人机航迹，考虑到变邻域搜索算法在求解大规模组合优化问题时具有求解快速和易实现的特点，本文在传统邻域算子的基础上，针对外卖配送的特点设计了几种邻域算子，用于优化骑手路径；A*算法是一种静态路网中常用的有向图启发式搜索算法，因为具有计算效率高、易实现、内存需求少、灵活性高等优点，被广泛应用在航迹规划和图搜索领域中，本文根据无人机避障问题的特点对A*算法加以改进，用于送餐无人机的航迹规划。两阶段算法框架如图3所示。

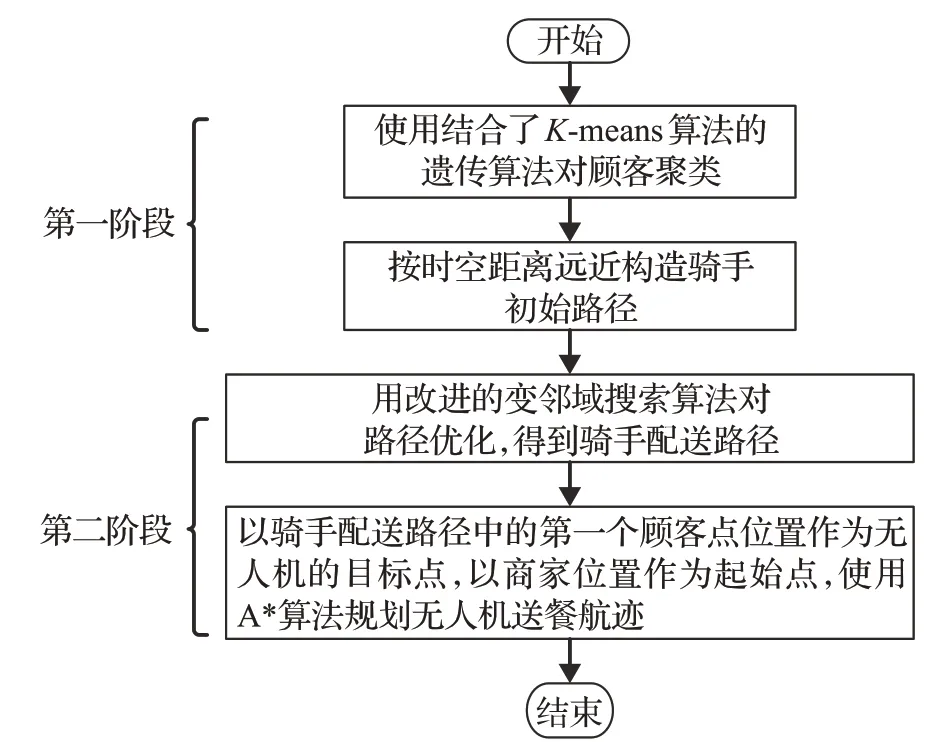
图3 两阶段算法框架Fig.3 Two-stage algorithm framework

3.1 构造考虑时空距离的初始路径

3.1.1 时空距离的定义

绝大多数的聚类算法在对顾客或配送点进行聚类时，通常只考虑了顾客点之间的地理位置这一因素，而并未将顾客点间的服务时间窗的差异考虑在内。然而在实际配送过程中，如果只考虑顾客的空间分布，将位置距离近的顾客安排在同一条路径上进行配送，当顾客点的服务时间窗差异较大时，则可能造成餐品不能准时送达；同理，如果只考虑顾客的时间窗，将时间窗相似的顾客安排在同一条路径上进行配送，当顾客空间距离相隔较远时，则可能无法达到最优解甚至可行解。基于此，本文在构造骑手送餐的初始路径时，同时考虑了顾客点的时间属性和空间属性。由于时间距离和空间距离的量纲不一致，本文基于文献[14]的研究构造时空距离，公式如下：

（1）若l i′＜e j，即骑手从顾客点i行驶至顾客点j后需要等待才能开始对顾客j的送餐服务，则顾客i与顾客j的时间距离可表示为行驶时间与平均等待时间之和，即

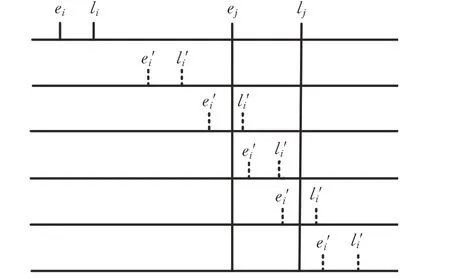
图4 顾客点间的时间窗关系示意图Fig.4 Schematic diagram of time window relationship between customer points

（2）若ei′＜e j≤l i′，即骑手有可能提前到达顾客点j，也有可能在顾客j的服务时间窗内到达，参考（1）的度量方法，顾客点i与顾客点j的时间距离可表示为

（3）若e j≤ei′且l i′≤l j，即骑手到达顾客点i的时刻完全位于顾客j的服务时间窗内，则将顾客点i与顾客点j的时间距离设为从顾客点i到顾客点j的行驶时间，即

（5）若l j＜ei′，即骑手从顾客点i行驶至顾客点j的时间完全晚于顾客j的预期最迟送达时间，这表明将该顾客点i与顾客点j安排在同一条路径上进行配送是不可行的，则将顾客点i与顾客点j的时间距离设为无穷大。

综上，时间距离的计算公式如下所示：

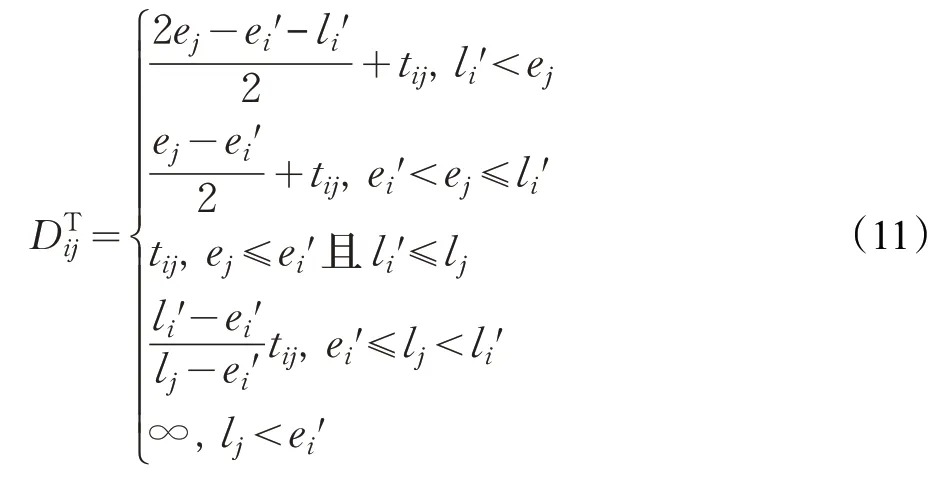
3.1.2 顾客聚类

聚类即将特征属性相似的个体划归为一组，使得组内个体的特征属性相似度尽可能大，而组间的尽可能小。由于K-means算法在对数据进行聚类时具有稳健快速等特点，故K-means算法是一种常用的数据聚类方法，但由于初始聚类中心的随机选取对聚类结果影响较大，本文采用结合K-means算法的遗传算法对顾客聚类，目标函数如式（12）所示，目的是使对所有的聚类簇，其他顾客点到聚类中心的时空距离之和最小。式中k为聚类数，即无人机的数量，z i为第i个聚类里的所有顾客点。

（2）根据式（11）计算顾客点间的时空距离。

（3）初始化种群。对种群中个体采用自然整数的十进制编码，个体的长度设为k，个体的每一位代表聚类中心，根据K-means算法的思想，当簇的中心确定时，可以根据就近原则对所有顾客分类。

（4）计算种群中个体的目标函数值，并将其作为个体的适应度值。

（5）种群进化。通过对个体的选择、交叉与变异来优化种群。

（6）判断是否满足终止条件。是，结束；否，返回（1）。

将时空距离替度量换为空间距离度量即为不考虑时空距离的顾客聚类。

3.1.3 骑手初始路径的构造

对顾客点完成聚类之后，以无人机的最大装载量作为约束，对顾客点按照离聚类中心时空距离最近的原则（或按照离商家空间距离最近的原则）进行配送，并对超过无人机最大装载量约束的顾客点重新分配，对每个聚类簇的初始路径构造如下：

（1）选取离聚类中心时空距离最近的顾客点并将其配送任务指派给骑手。

（2）以无人机最大装载量为限制条件对剩余顾客点按时空距离由小到大依次进行指派，对违反无人机装载量约束限制的顾客点执行步骤（3）。

（3）按照该顾客点与其余无人机停靠点时空距离由小到大的顺序，依次检测其他聚类簇的无人机剩余装载量是否满足该顾客点的送餐量需求，若满足，则将顾客点指派给该聚类簇；否则，令k=k+1，并将该顾客点划归到一个新的聚类簇中。

（4）检测是否还有未进行指派的订单，若有，则返回（1）；若无，结束并输出初始路径。

如对顾客点按照离商家空间距离最近的原则进行配送，即为不考虑时空距离时仅骑手配送模式下的骑手初始路径构造。

3.2 骑手路径优化

3.2.1 变邻域搜索算法

变邻域搜索算法是一种基于局部搜索的元启发式算法，其基本思想是在搜索过程中系统地改变当前解的邻域结构以扩展搜索范围，接着通过局部搜索求得局部最优解，基于此局部最优解重复上述过程，经过若干次迭代之后最终达到收敛的目的。本文在传统的变邻域搜索算法的基础上，结合外卖配送过程中顾客位置临近、送餐时间窗相似等特点，对传统邻域结构和局部搜索算子进行改进。图5描述了变邻域算法的基本流程，其中x b表示当前时刻的最优解，F(x)表示任意解x的目标函数值。本文在求解过程中，通过以一定概率接受较差解的方法扩大解空间，从而提升算法跳出局部最优解的能力。

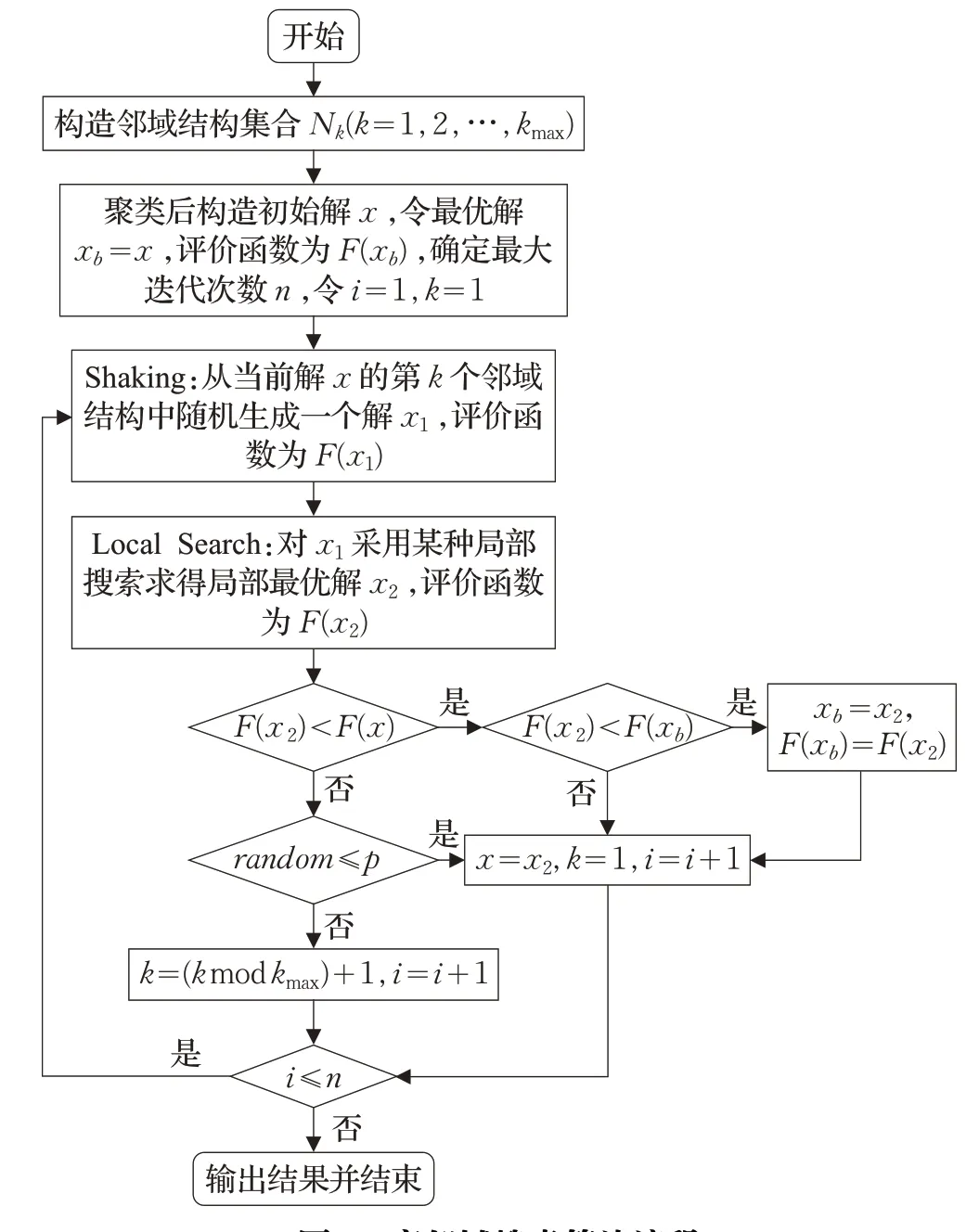
图5 变邻域搜索算法流程Fig.5 Flow chart of VNS

3.2.2 邻域构造

为了扩展当前解的搜索空间，扩大解的多样性，减少算法陷入局部最优的可能性，本文采用Relocate和Exchange两种邻域结构。Relocate表示在某条路径上选取一个或几个连续的节点，从当前路径随机转移到另一条路径中；Exchange表示在任意两条路径上交换数量相同的连续节点。两种邻域结构分别如图6所示。

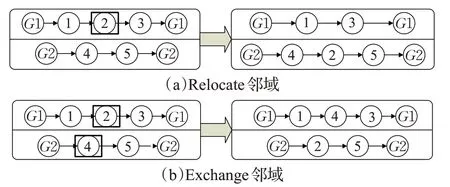
图6 两种邻域结构Fig.6 Two neighborhood structures

3.2.3 局部搜索

在邻域结构抖动后，运用局部搜索对产生的新的路径进行优化，求得局部最优解。本文采用Insert、2-opt和Reverse三种局部搜索算子，Insert表示把一个或几个连续的节点插入到这条路径上的其他位置，2-opt表示在同一条路径上选取任意两点位置互换，Reverse表示在一条路径选取几个连续的节点进行倒序。三种局部搜索算子如图7所示。

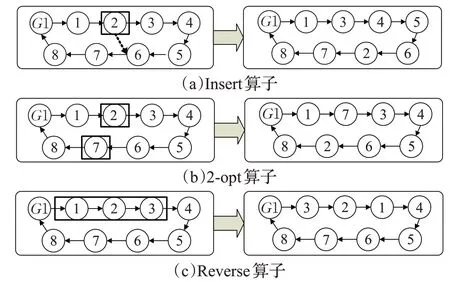
图7 三种局部搜索算子Fig.7 Three local search operators

3.2.4 新解的接受策略

为了进一步提升算法跳出局部最优的能力，本文借鉴模拟退火算法的解的接受规则，以一定的概率接受较差解，避免算法过早地陷入局部最优。令x表示当前解，x2为x经过邻域抖动和局部搜索之后的局部最优解，令ΔF=F(x2)-F(x)，若ΔF≤0则进一步比较F(x2)与F(xb)的大小关系；若ΔF＞0，则以一定的概率p=e-ΔF/T接受x2并更新当前解x至x2。为了使算法在迭代初期跳出局部最优的能力较强而在迭代末期算法趋于稳定，本文令温度T线性变化，迭代第r次后，T=Tmax(1-r R)，其中Tmax为初始温度，R为最大迭代次数。

3.3 送餐无人机避障航迹规划

在无人机越来越多地应用于送餐、航拍等民用领域的同时，相关部门也制定了若干无人机飞行管理规定，考虑到城市建筑物高度可能大于无人机飞行高度等情况，规避障碍物成为了无人机路径规划中十分重要的一个方面。无人机在巡航时要与规避对象保持一定的安全距离，即留有安全裕度l。由于城市中的高楼形状规则，因此为了简化飞行环境，可以在立体平面中取飞行平面，在二维平面中进行无人机航迹规划。A*算法是一种静态路网中常用的有向图启发式搜索算法，因为它计算效率高、易实现、内存需求少、灵活性高以及对不同路况超强的适应能力，A*算法被广泛应用在航迹规划和图搜索邻域中。

3.3.1 A＊算法

A*算法通过搜索当前位置的临近节点，选取代价值最小的节点作为扩展节点加入搜索空间，新加入的节点又能产生新的可扩展节点，直到目标点被选作扩展节点，再从目标节点逆向溯源，找到从起始点到目标点代价最小的路径。A*算法中节点n的代价函数为：

其中，f(n)为待扩展节点的评估函数，表示从起始点经节点n到达目标点的估计代价，g(n)为从起始点到当前节点n的实际代价，h(n)表示从当前节点n到目标点的代价估值。A*算法扩展下一节点时，从待选节点中选择估计代价值f(n)最小的节点插入到路径链表中。

针对二维平面无人机避障航迹规划问题，本文对A*算法做如下设计。设置无人机的起飞点S和降落点G和各障碍区域的节点信息，建立两个存储节点信息的空列表OPEN LIST和CLOSE LIST。由于目标是使无人机飞行距离最小，故式（13）中考虑的代价是无人机的航程，g(n)表示从起飞点S到节点n避过障碍物的已飞航程，h(n)表示不考虑障碍区域从当前节点n到降落点G的直线距离y n、y G分别为当前节点n和降落点G的横纵坐标。算法具体步骤如下：

（1）输入起飞点、降落点以及障碍区域的节点信息，判断从起飞点到降落点直线飞行是否穿过障碍物，若是则将起飞点信息存入OPEN LIST中，转（2）；若否则直接结束。

（2）遍历当前OPEN LIST，找到f(n)最小值对应的节点并展开，即找到从该节点到降落点穿过的第一个障碍物，将该障碍物的可用节点信息放入到OPEN LIST中，同时把OPEN LIST中已展开的节点放入到CLOSE LIST中。

（3）重复（2），当OPEN LIST中的展开点与降落点之间没有障碍物（即障碍物的节点信息为空）或OPEN LIST为空时结束循环。

3.3.2 航迹修复

通过上述过程得到航迹可能存在从起飞点到路径中某个节点直线连接不穿过障碍区域的情况，因此需要对上一小节所得的航迹做检查修复。如图8所示，假设得到的航迹节点序列为X=[X1,X2,…,X n]，如果从节点X i到节点X k(1≤i＜k≤n)直线飞行不经过障碍物，则节点X i与节点X k之间的所有节点都是冗余节点，将冗余节点从航迹节点序列中删除。遍历所有节点，把删除冗余节点后的序列作为修复后航迹节点序列。

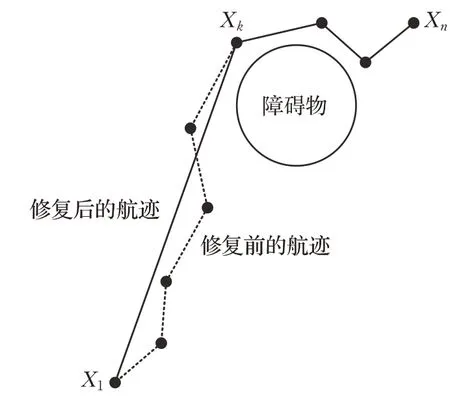
图8 航迹修复示意图Fig.8 Schematic diagram of track correct

对航迹检查修复后可以规划出一条由航迹节点依次连接而成的无人机折线飞行路径，但在航迹节点处存在转折角，由于四旋翼无人机具备空中悬停功能，不用考虑最大转弯角和最小转弯半径约束。

综上，送餐无人机避障航迹规划的算法流程如图9。

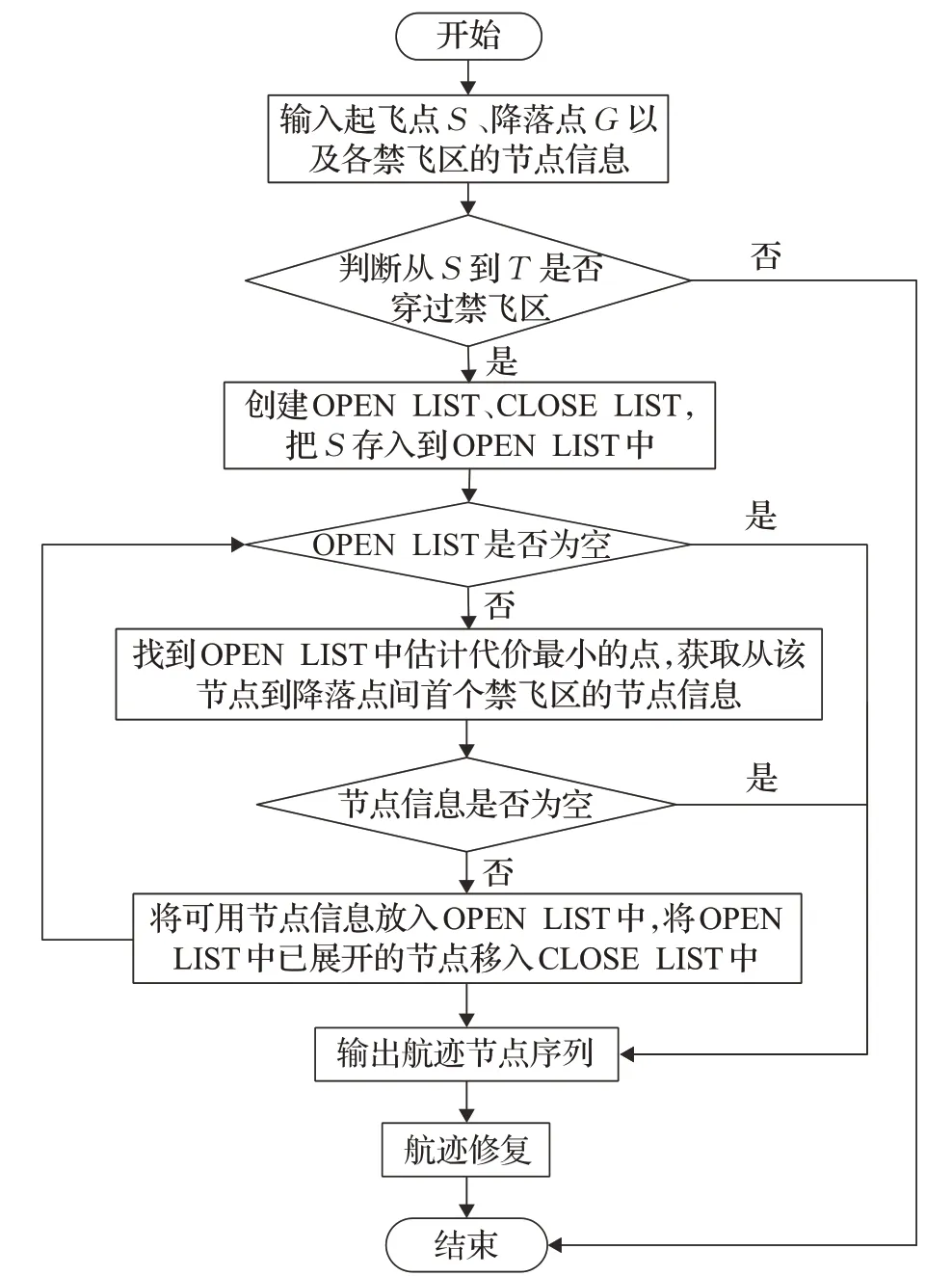
图9 无人机航迹规划算法流程Fig.9 Flow chart of drone track planning

4 实验结果及分析

4.1 算例说明与参数设置

由于目前还没有关于外卖配送的标准案例，本文以武汉市某美团外卖商家为研究对象，获取该商家在12：00至12：30时间段内接收的外卖订单数据，生成订单数量分别为25、30、35、40、45的五组算例作为实际案例进行计算。外卖一般送达时间为45 min，在30 min内接收若干订单后，餐品的预期送达时间还剩15～45 min，考虑到餐品出餐、包装等过程，本文将配送时预期送达时间Ti的最小值设为10 min，最大值设为40 min，最迟送达时间Ti′=Ti+10。实验参数设置如下：t s=2 min，s=40 km/h，Q=10，a=0.2，b=0.3，c1=0.5，c2=1，l=10 m。算法编程采用MATLAB R2018b，操作系统为Windows 10，电脑内存为8 GB，CPU为Intel i7-7700M，主频3.60 GHz。

4.2 实验结果对比分析

为了验证聚类时考虑时空距离对于减少配送成本和提高准时送达率的有效性以及无人机骑手联合外卖配送模式相较于仅骑手配送模式的优越性，本文通过对上述五组算例R1（25）、R2（30）、R3（35）、R4（40）、R5（45）分别在不考虑时空距离和考虑时空距离的情况下进行求解，实验结果如表1、表2所示。

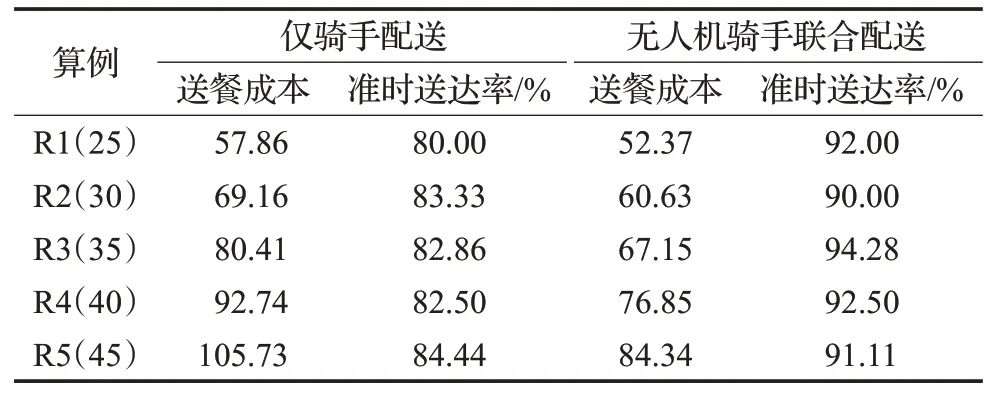
表1 不考虑时空距离的实验结果Table 1 Results without considering temporal-spatial distance

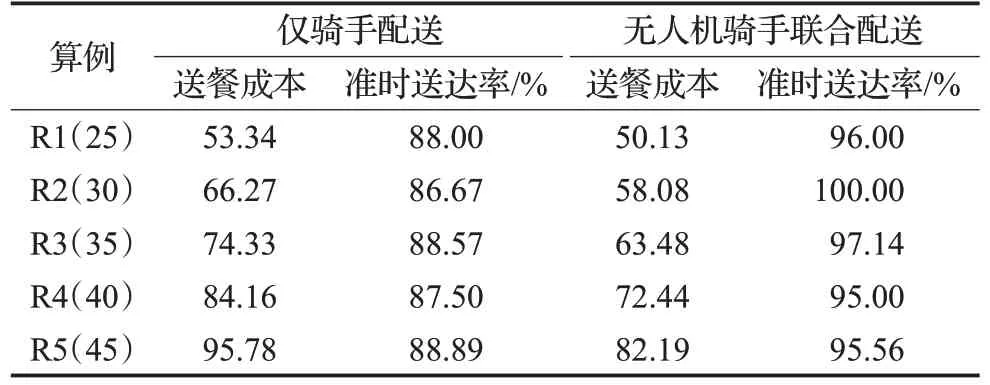
表2 考虑时空距离的实验结果Table 2 Results considering temporal-spatial distance

可以看出，不论是仅骑手配送模式还是无人机骑手联合配送模式，对同一算例而言，考虑时空距离后的送餐成本更少、准时送达率更高；此外，不论是否考虑时空距离，对于同一算例而言，与仅骑手配送模式相比，无人机骑手联合配送模式下的送餐成本更少，送达准时率更高。实验结果证实了考虑时空距离对减少送餐成本、提高准时送达率的有效性以及无人机骑手联合外卖配送模式相较于传统仅骑手配送模式的优越性。

选取算例R3（35）对求解过程做具体说明。R3（35）订单数据如表3所示，禁飞区位置坐标如表4所示，商家、顾客在地图中的位置如图10所示。

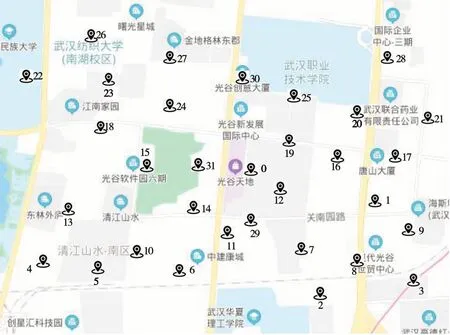
图10 商家、顾客在地图中的标识Fig.10 Merchant and customers in map

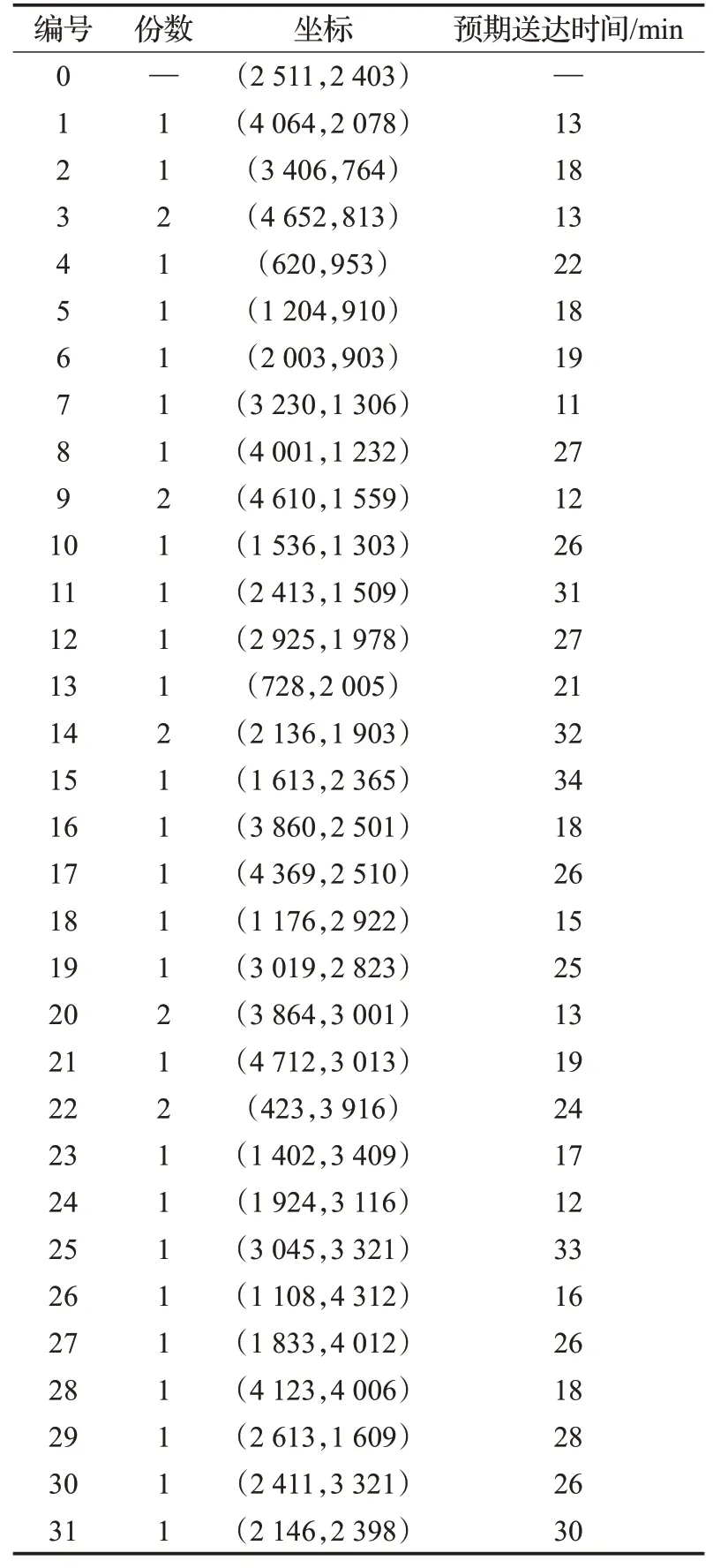
表3 订单信息Table 3 Orders details

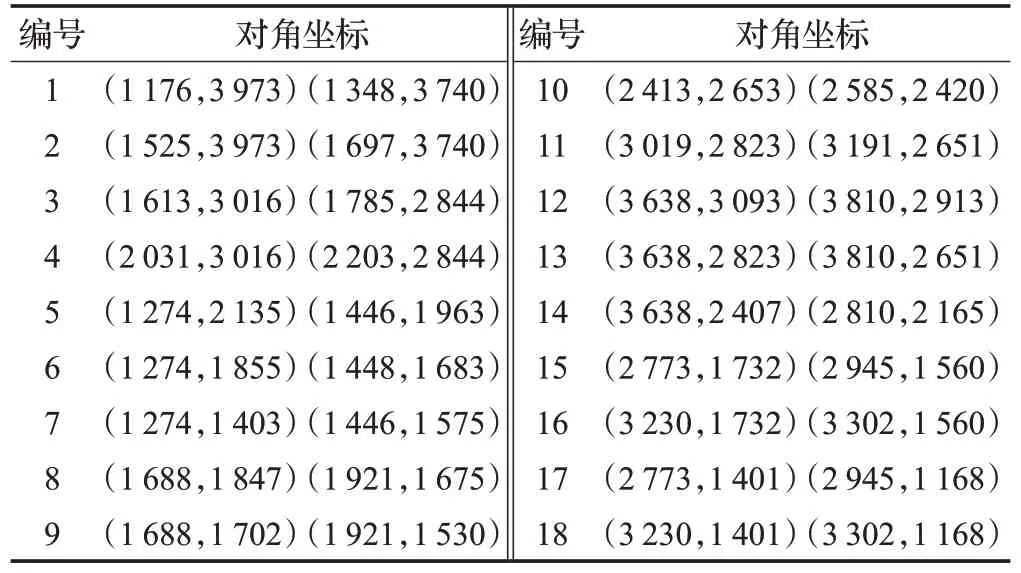
表4 各禁飞区对角坐标Table 4 Diagonal coordinates of no-fly zones

分别求解在不考虑时空距离情况下仅骑手配送模式和考虑时空距离情况下无人机骑手联合配送模式的送餐成本和准时送达率。首先分别使用不考虑时空距离和考虑时空距离的K-means算法对上述顾客点进行聚类，得到骑手初始路径，结果如表5（括号内表示聚类中心）、表6所示。使用变邻域搜索算法对初始路径进行优化，得到两种模式下骑手的送餐方案，在仅骑手配送模式下的目标值和准时送达率分别为74.59和87.10%，在联合配送模式下的目标值和准时送达率分别为58.71和96.77%，送餐路径如图11所示，具体信息见表7（括号内表示未能准时送达的订单）。

表7 优化后的骑手路径Table 7 Optimized rider path

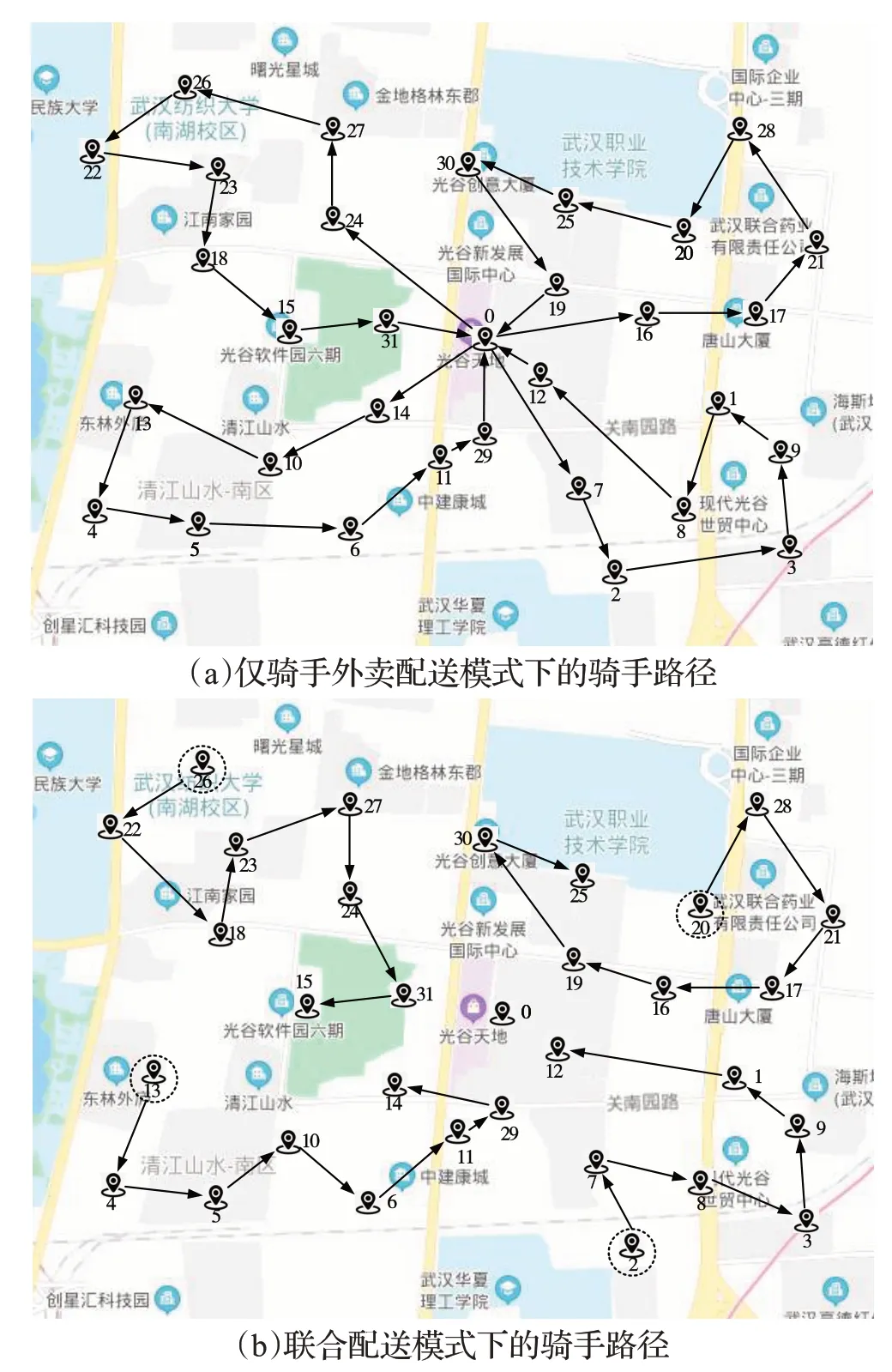
图11 两种模式下的骑手路径Fig.11 Rider path in two modes

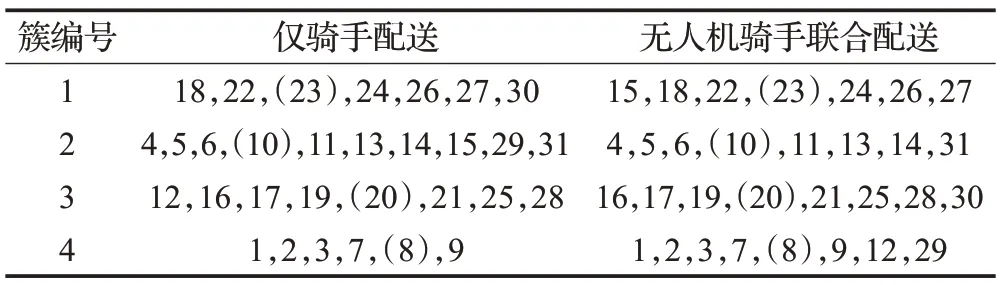
表5 聚类结果Table 5 Customer clustering

表6 骑手初始路径Table 6 Rider initial path

以商家位置为起点、以无人机骑手联合配送模式下的骑手出发点作为终点，使用A*算法对无人机路径进行规划，航迹如图12，具体信息如表8所示。

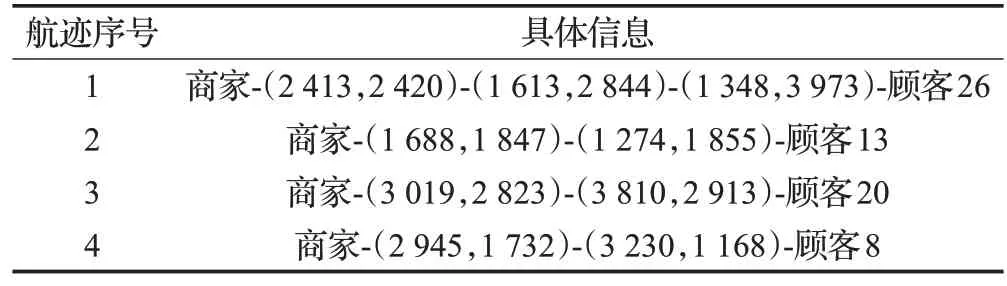
表8 航迹节点信息Table 8 Track nodes

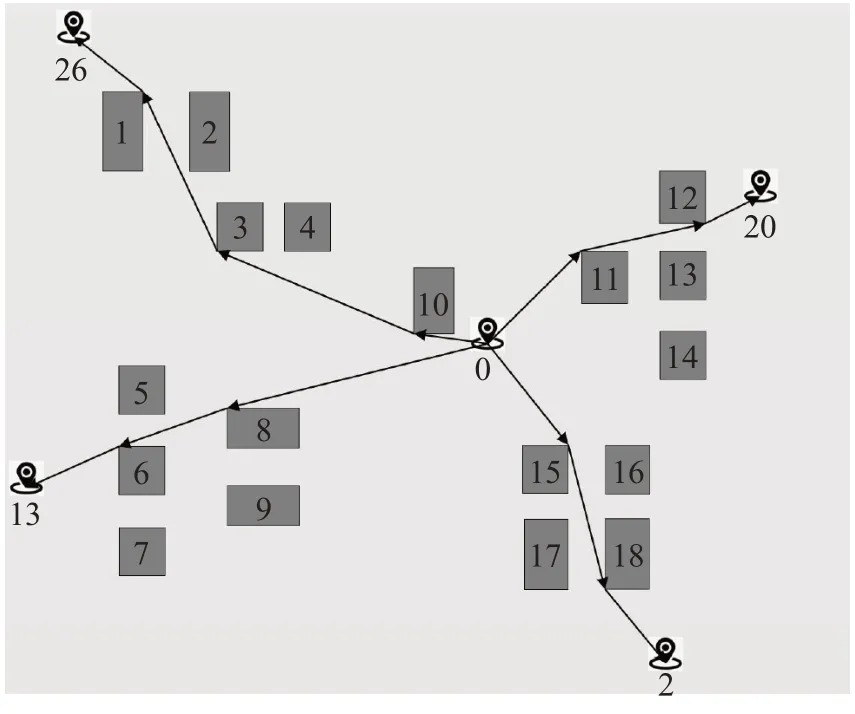
图12 无人机避障航迹Fig.12 Drone obstacle avoidance track

4.3 算法性能对比分析

为验证改进后变邻域搜索算法（AVNS）的有效性，在考虑时空距离的无人机骑手联合外卖配送模式下，对上述R1、R3、R5三种不同规模的实验案例，再分别使用变邻域搜索算法（VNS）、遗传算法（GA）和蚁群算法（ACO）进行求解，各运行50次，实验结果如表9所示。对比四种算法的求解结果，发现在计算时间上，AVNS算法并非最短，但在任意一个算例下，AVNS算法均能收敛到较好的最优解，并且GA、ACO和VNS求得的最差值、平均值、标准差和平均准时率明显差于AVNS算法，这意味着AVNS算法较其他三种算法有更好的稳定性。上述实验结果证实了改进后变邻域搜索算法在求解外卖配送路径优化问题时的合理性及有效性。

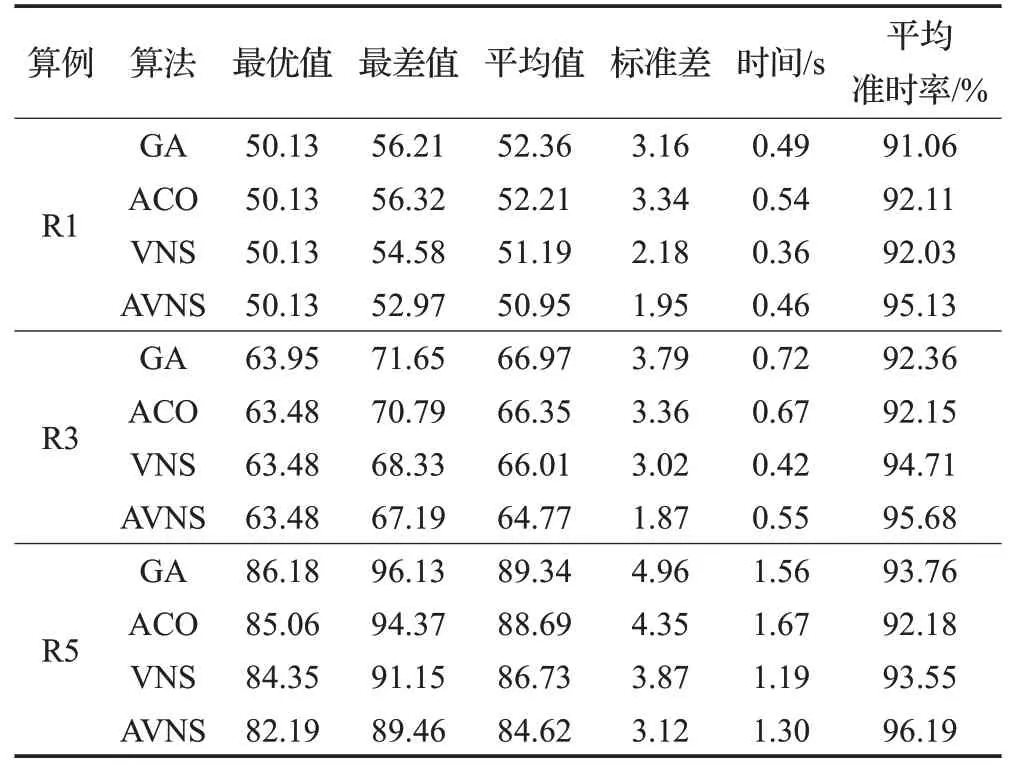
表9 算法实验结果对比Table 9 Comparison of algorithm experimental results

5 结束语

本文根据外卖配送领域出现的一种新兴的配送模式，以最小配送成本为目标构建了无人机骑手联合外卖配送模式的路径优化问题模型。针对模型设计了一种先聚类后优化的两阶段启发式算法，使用考虑了时空距离的K-means算法对顾客点聚类，分别使用改进的变邻域搜索算法与A*算法对骑手路径与无人机航迹进行规划，通过多组算例实验结果对比分析验证了聚类时考虑时空距离对较少配送成本的有效性以及无人机骑手联合外卖配送模式相较于仅骑手配送模式的优越性。最后通过求解从武汉某美团外卖商家获取的实际算例，验证了本文提出的两阶段算法在真实外卖配送情景中的有效性。当前研究还存在一些有待改进之处，如：考虑多个商家共同配送、考虑出餐时间的不确定性、考虑无人机在三维空间中的路径规划、考虑顾客满意度等，在后续的研究中将重点考虑这些因素。