大空间下送风夏季非稳态全热B-G模型研究
黄 晨 朱继阳 杨 通 王 非 邹志军 范钱宏 苗宇峰
(1 上海理工大学环境与建筑学院 上海 200093;2 同济大学建筑设计研究院有限公司 上海 200092)
相关研究发现大空间建筑分层空调负荷与室内热湿环境紧密相关[1],夏季空调负荷应采用不稳定逐时计算方法,但长期以来大空间分层空调负荷难以按逐时方法计算。因此,建立大空间非稳态热湿环境模型是必要的。
国内外学者通过理论建模来研究室内热环境,弥补了数值模拟和实验方法针对特定建筑研究的不足。在大空间建筑热环境的建模研究中,常见的简易分区模型有节点模型、Block模型等。节点模型有基于空气温度的三节点模型、四节点模型、多节点模型[2-5],以研究高大空间竖直方向上的温度分层现象。Block模型目前已逐步发展到空气温度与建筑内壁面温度耦合求解的稳态B-G模型[6-14]。然而实际的大空间建筑,影响热环境的因素是不稳定的,室内常有散湿现象。但大多研究均采用稳态并忽略室内散湿现象,与实际不符。要实现与实际接近的大空间空调负荷逐时计算,首先要建立非稳态扰量作用下的大空间热湿环境预测模型。
本文以温度型稳态B-G模型为基础,建立夏季非稳态的全热B-G模型,并通过一实际大空间建筑在下送风分层空调的情况下,现场实测竖直方向的温湿度分布、焓值分布进行验证。
1 大空间下送风非稳态全热B-G模型
由于建筑和空气的蓄热特性,大空间建筑在不稳定扰量作用下,室内热湿环境也会不稳定。本文在能量方程中,采用谐波法计算考虑建筑蓄热特性的内壁面温度,通过现场不稳定实验获得代表空气蓄热特性的室内空气变化,同时考虑室内散湿,在原有稳态温度型B-G热环境预测模型基础上,建立非稳态全热B-G模型。
1.1 温度型Block模型关键公式
温度型B-G中Block模型是建立在室内竖直方向上各空气区域的质量和能量平衡提出的,主要由壁面流模型、主流区模型和相邻区域换热模型3部分组成。Block模型的基本构成如图1所示,i为主流区i层;k为4个围护结构的编号;qw(i,k)为室外通过围护结构传入建筑的热量,W;qcond(i)、qc(i)分别为主流区i+1层与i层之间由于温差或空气对流引起的换热量,W;t(i)、θ(i,k)分别为主流区i层空气温度和主流区i层k壁面温度,℃。在壁面流中存在如下关系:
md(i,k)+min(i,k)=md(i-1,k)+mout(i,k)
(1)
tm(i,k)=[md(i-1,k)tm(i-1,k)+
mout(i,k)td(i,k)]/[md(i,k)+min(i,k)]
(2)
式中:md(i,k)为主流区i层周边k壁面边界层中壁面流的质量流量,kg/s;min(i,k)、mout(i,k)分别为k壁面附近的边界层向主流区i层流入和流出的质量流量,kg/s;md(i-1,k)为主流区i-1层周边k壁面边界层中壁面流的质量流量,kg/s;tm(i,k)、td(i,k)分别为主流区i层周边k壁面边界层中壁面流和边界层内空气平均温度,℃;tm(i-1,k)为主流区i-1层周边k壁面边界层中壁面流平均温度,℃。上述物理量均可根据壁面流热质平衡方程获得[15]。

图1 同步求解模型的基本构成Fig. 1 The basic constitution of synchronous solution model
主流区各层之间存在如下关系:
qc(i)=cpmc(i+1)[t(i+1)-t(i)]+
cpmc(i)[t(i-1)-t(i)]
(3)
qcond(i)=CBAB(i+1)[t(i+1)-t(i)]+
CBAB(i)[t(i-1)-t(i)]
(4)
式中:cp为空气定压比热,J/(kg·K);mc(i)为主流区i层空气流入主流区i-1层的质量流量,kg/s;mc(i+1)为主流区i+1层空气流入主流区i层的质量流量,kg/s;CB为区域温差传热系数,取值为2.3 W/(m2·℃)[16];AB(i)为主流区i层与i-1层区域分界面面积,m2;AB(i+1)为主流区i+1层与i层区域分界面面积,m2;t(i+1)为主流区i+1层空气温度,℃;t(i-1)为主流区i-1层空气温度,℃。
1.2 非稳态全热Block模型
假定室内空气无蓄湿特性,引入含湿量概念,建立各区域的湿量质平衡方程:
md(i-1,k)d(i-1)-md(i,k)d(i)-
mc(i)d(i)+mc(i+1)d(i+1)=0
(5)
式中:d(i)、d(i-1)、d(i+1)分别为主流区i层、i-1层、i+1层的空气含湿量,g/(kg干空气)。将1.1节温度求解的Block模型更改为考虑室内散湿量的焓值模型;忽略dg(或dkg)湿量同时带进空气的显热,即湿空气焓值h(i)(kJ/kg):
h(i)=[cpt(i)+2 500d(i)]/1 000
(6)
考虑空气蓄热特点,各主流区域能量平衡方程如下:
cpAB(i)ΔH(i)ρ(i)[t(i)-t′(i)]/Δτ=βiQ(i)+
(7)
式中:ΔH(i)为主流区i层的区域高度,m;ρ(i)为主流区i层空气密度,kg/m3;t′(i)为主流区i层空气前一时刻温度,℃;Δτ为相邻两个时刻的时间间隔,s;βi为主流区i层热源散热量中对流散热量占比;Q(i)为主流区i层热源散热量,W;m为主流区i层内壁面个数;hM(i,k)为k壁面流入Blocki的空气焓值,kJ/kg;ΔD(i)为主流区i层散湿量,kg/s;hv(i)、γ(i)为主流区i层水蒸气比焓和水的汽化潜热,kJ/kg;h(i-1)、h(i+1)为主流区i-1层、i+1层湿空气焓值,kJ/kg。
式(5)、式(7)计算时,需根据各分区的具体情况增加相应的送风项、回风项、湿源散湿项等携带的能量,具体可参考文献[15]。
采用多工况不稳定实验的空气温度变化平均值确定式(7)左侧空气蓄热量。由于不同区域温度变化不同,因此,空气蓄热量是一个在不同区域不同时间的二维变量。
1.3 B-G模型中墙体壁温的非稳态处理
Gebhart模型是考虑一次反射辐射后的辐射模型[17],对于实际建筑所处的近似呈周期性谐波变化的室外环境,因围护结构的蓄热特性,致使外壁面得热不等于内壁面放热,室外周期性扰量Tz,τ(℃)为:
(8)
Tz,τ=Tzp+ΔTzcos(ωτ+φ)
(9)
式中:Tair,τ为逐时室外空气干球温度,℃;a为围护结构外表面对太阳辐射的吸收率;Iτ为太阳辐射照度,W/m2;αout为围护结构外表面传热系数,W/(m2·K);Tzp为室外空气综合温度日平均值,℃;ΔTz为室外空气综合温度变化波幅,℃;ω为外扰频率,ω=2π/T,rad/h;τ为扰量周期,h;φ为综合温度初相位,rad。
引入谐波法,考虑墙体蓄热特性,对围护结构非稳态传热量进行一维简化求解。室内内壁面温度θτ(℃)可表达为一个稳定值加波动值的周期函数形式:
θτ=θp+Δθτ
(10)
(11)
式中:θp为内壁面温度平均值,℃;Δθτ为内壁面温度波动值,℃;νn为围护结构室外空气综合温度扰量传至内表面的衰减度;ζ为围护结构室外空气综合温度扰量传至内表面的延迟时间,rad。νn、ζ可通过手册查取[18]或计算确定[19]。
由式(10)、式(11)可知,到任意主流区i层k壁面的对流换热量qd(i,k)(W)为:
qd(i,k)=αd{t(i)-[θ(i,k)+Δθτ(k)]}
(12)
式中:αd为主流区与壁面间的表面传热系数,W/(m2·K);θ(i,k)为主流区i层k壁面温度的稳定部分,即式(10)中的θp;Δθτ(k)为k壁面温度波动值,℃。
假设室内还存在热源,室内任一主流区i层k壁面得到的净辐射热量qR(i,k)(W)为:
[θ(i′,k′)+Δθτ(k′)]}
(13)
式中:n为Block模型区域划分数;i′代表除主流区i层之外的其它空气层;βi′为主流区i′层内的热源散热中对流散热占比;φi′(i,k)为主流区i层k壁面与主流区i′层内热源Q(i′)之间的角系数;Tm为壁面总流的平均温度,℃;ε(i,k)为主流区i层k壁面辐射系数;σ为黑体辐射常数,值为5.67×10-8W/(m2·K4);Gik,i′k′为主流区i层k壁面与主流区i′层k′壁间的Gebhart系数;θ(i′,k′)为主流区i′层k′壁面温度的稳定部分,℃;Δθτ(k′)为k′壁面温度波动值,℃。
Block 主流区i层k壁面与室外空气之间的换热量qλ(i,k)(W)为:
qλ(i,k)=K[Tzp-t(i)]+αdΔθτ(k)
(14)
式中:K为壁面总传热系数,W/(m2·K)。
Block主流区i层中k壁面的能量平衡方程式可写为:
αd{t(i)-[θ(i,k)+Δθτ(k)]}+K[Tzp-t(i)]+
Δθτ(k′)]}=0
(15)
对于矩形建筑,若竖直方向Block模型分为6个区域,则水平方向分东西南北4个朝向,外加地面和屋顶,共有26(4×6+2)个壁面能量平衡方程。
1.4 非稳态全热B-G修正模型的建立
以非稳态扰量瞬时值作为边界条件,利用所建瞬态全热B-G模型可以获得该时刻的热环境解,在一系列的非稳态扰量逐时值的边界条件下,获得一系列的逐时热环境解,将该系列的热环境解联合起来,组成非稳态的热环境解。对于一个6区B-G模型,可联立6个Block空气能量平衡方程(式(7));26个壁面Gebhart能量平衡方程(式(15));6个焓方程(式(6))。构成了同步求解室内竖直壁面以及空气温度分布的38个能量方程。
2 研究对象及实验方案
2.1 大空间建筑研究对象
本研究对象为一幢实际建筑面积为500 m2、坡屋顶最高点和最低点距室内地面分别为12 m和9.6 m的大空间热环境实验基地,实景及物理模型如图2所示。

图2 某大空间建筑热环境实验基地(下送风分层空调)Fig. 2 A large space building thermal environment experiment base (undersupply stratified air conditioning)
实验基地采用下送下回分层空调气流组织形式,室内设有8个柱状下送风口,分别落地靠南墙和北墙放置,南北各4个。回风口设于空调机房东侧。在建立实验基地物理模型时,将坡屋顶简化为矩形建筑,竖直方向划分6个区域,空调区1个分区,高度为2.6 m(回风口高度),非空调区5个分区,最高处第5区、第6区高度分别为1.5、0.7 m(将坡屋顶等体积为平屋顶换算的当量高度)。
2.2 实验方案
实验过程中,室外空气的温湿度由精度为±0.2 ℃、±2.5% RH的室外气象站测量,太阳辐射通过精度为±2%太阳辐射仪测量。室内高度3 m以上的固定竖直温度测线如图3所示。由图3可知,共有3排固定竖直温度测线,各测线测点间距为1 m,根据坡屋顶高度不同单排有7个或8个测点,A、C、E、I、K竖直温度测线旁布有5根竖直温湿度测线,在Block 2~5区域中点布置。在人员活动的空调区,设置移动测杆,布置点与3 m以上固定测线为一竖直线,分别在高度为0.1、0.3、1.1、1.7 m设4个温度测点,同时在1.1 m处布置湿度测点。固定温度测线由精度为±0.2 ℃的Pt1000传感器直接采集。移动测杆采用精度为±0.3 ℃的E+E温度计和精度为±0.1 ℃的玻璃温度计测定,湿度测定采用精度为±3% RH的TH20温湿度计,测试时各区4个朝向的壁面、屋顶以及地板的壁面温度均采用精度为±0.1 ℃的热线测温仪多点测定,所用温湿度采集时间间隔均控制为20 min。实验前所有仪器都经过实验室标定和校正。

图3 室内温度测线Fig. 3 Floor plan of indoor temperature measurement line
表1所示为实验测试工况及参数,由于各工况实验起始时间不一致,下列各工况均整合至09∶40为实验的开始。表1中各参数为整合后15∶00时8个工况在不同室外温度、送风量、散湿量条件下的实验值。以Case 5为例,图4所示为不同时刻的太阳辐射照度和室外温度变化。

表1 实验工况Tab. 1 Experimental condition

图4 Case5不同时刻的太阳辐射照度和室外温度变化Fig. 4 Solar irradiance and outdoor temperature changes at different times of Case5
3 结果与讨论
式(7)中不同时间不同区域的室内空气温差,由8个实验工况结果取均值获得,温差均方根误差(root mean square error,RMSE)采用式(16)表示。为定量评估理论计算模型预测值与实验测量值间的误差,采用式(17)、式(18)对平均绝对误差(mean absolute error,MAE)和平均绝对相对误差(mean absolute relative error,MARE)进行评估。
(16)
(17)
(18)

3.1 室内非稳态温度模型预测与实验结果
不同工况下同一区域温度变化特征具有相似性,图5所示为8个工况各区域空气温差实验均值随时间的变化。空气温差是指不同区域前后时刻空气温度差。由图5可知,空调开启至12∶20期间,空气温差波动剧烈,12∶20以后各区域的空气温差变化平缓。且随高度增加,空气温差越大,空气蓄热量也越大。
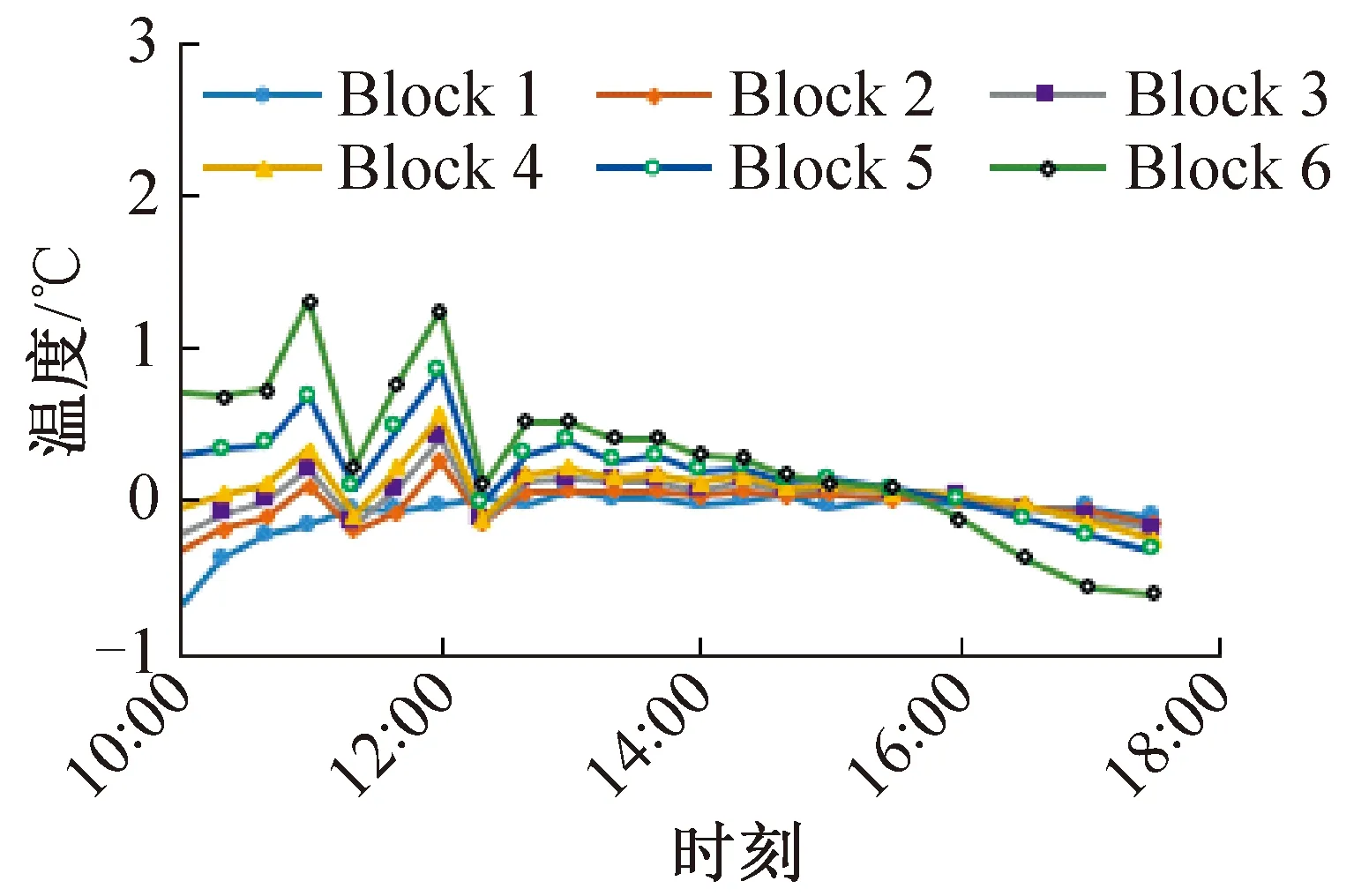
图5 8种工况下各区域空气温差实验均值随时间的变化Fig. 5 Variation of experimental mean value of air temperature difference in each region with time under 8 working conditions
由图5和式(16)得到8个工况下前后温差在整个实验期间均方根误差在0.025~0.048 ℃,因此,图5中不同高度的温差可以作为式(7)空气蓄热项的依据。
图6所示为Case 5各区域空气温度实验值与模型计算理论预测值随时间的变化。“th”为理论计算值,“ex”为实验值。由图6可知,实验过程中,1~4区不同时间绝对误差的平均值在0.38~1.48 ℃,5区、6区分别为2.55 ℃和3.79 ℃。造成理论值与实验值存在误差的主要原因是Block模型在空气与壁面换热处理上,借助了壁面流作为中间媒介,但在空气与屋顶壁面处理时采用直接换热的方式,且非空调区接近屋顶处有窗户渗透风作用,窗户渗透作用未在模型中体现等。

图6 Case5不同高度空气温度理论与实验值随时间变化的对比Fig. 6 Comparison between theoretical and experimental values of Case5 air temperature at different altitudes
3.2 室内竖直方向热环境模型解与实验结果对比
图7所示为8个工况在15∶00时刻所建非稳态全热B-G模型计算所得竖直方向空气温度与壁面温度的分布。由理论值与实验值对比可知,两者趋势基本一致,理论值与实验值在空调区的温度梯度整体略小于非空调区,实验值更显著。这是因为空调区受空调送风直接影响,下部空调区空气在不断地与送入的空调冷风混合,使下部空调区空气分布均匀,不易受干扰波动。对比理论值与实验值可知,大部分空气温度理论值略小于实验值,各工况在近屋顶附近,空气温度与壁面温度偏差较大,与图6所示现象类似。

图7 不同工况15∶00室内垂直空气温度与壁面温度的理论值与实验值对比Fig. 7 Comparison of theoretical and experimental values of indoor thermal environment at 15∶00 under different working conditions
表2所示为8个工况不同区域空气温度、壁面温度、空气焓值的理论值与实验值采用式(17)、式(18)计算得到的MAE和MRAE值。由表2可知,1~4区的空气温度、壁面温度、空气焓值的MAE分别为0.44 ~1.12 ℃、0.63~1.96 ℃、1.85~4.96 kJ/kg,MRAE分别为1.95%~3.49%、2.06%~6.26%、3.80%~7.90%,5区、6区误差较大,空气温度、壁面温度高达13%,空气焓值可高达30%,与上述相关计算结果一致,为后续模型完善提供了思路。由竖直方向最大平均误差计算结果发现,Case 2和Case 8计算值误差较大。
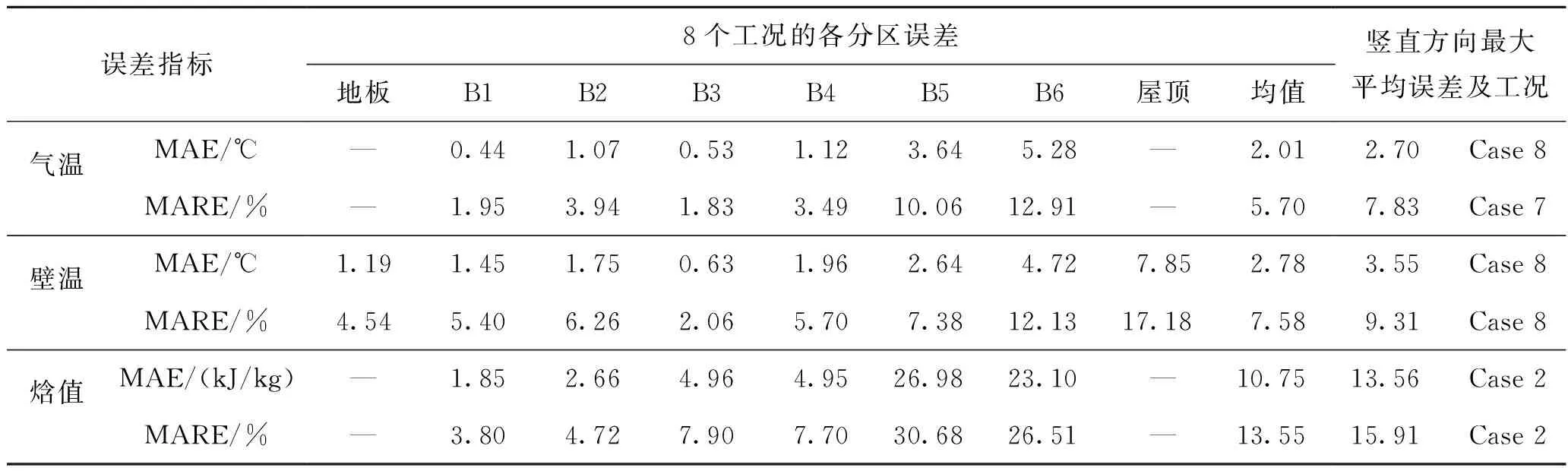
表2 8个工况热环境各分区15∶00时MAE和MARE及其最大误差工况Tab. 2 MAE and MARE and their maximum error conditions at 15∶00 in each zone of 8 working conditions
4 结论
本文考虑围护结构的蓄热特点,采用谐波法计算围护结构内壁面温度,利用各实验工况空气温差平均值计算空气蓄热量,建立了求解大空间分层空调非稳态热湿环境的6区域全热B-G模型。针对研究对象8个工况的实验结果,对比了空调开启与室外非稳态扰量影响下的模型预测准确程度,得到如下结论:
1)各实验工况温差均方根误差在0.025~0.048 ℃之间,表明利用实验工况温差平均值计算空气蓄热项的方法是可取的。
2)8个工况的空气温度、壁面温度及焓值的理论值与实验值趋势基本一致。竖直方向上的6区中,1~4区理论值与实验值误差较小,各工况空气温度和壁面温度的理论预测值与实验值平均绝对误差MAE分别为0.44 ~1.12 ℃、0.63~1.96 ℃,室内空气焓值为1.85~4.96 kJ/kg,各工况接近屋顶的5区和6区的误差较大,并呈现出高度越高,误差越大的趋势。
3)所建模型在大空间竖直方向中下部理论预测值与实验值较为吻合,采用谐波法与实验结果考虑大空间热环境不稳定解是可行的。模型计算结果在近屋顶处较大偏差将为后续模型进一步完善提供改进思路。

