接地极接地电阻计算公式应用分析与推荐公式
戴勇干
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
0 前 言
敷设于全空间、半空间及埋深为h等几种情况的垂直接地极和水平接地极,其工频接地电阻计算在很多文献[1-3]中基于接地极理想模型采用中点电位法和平均电位法来进行推演,从而得到不同敷设方式的接地极接地电阻近似计算表达式。当接地极满足l≫d/2或l≫2h≫d/2时可以得到如规范[4-6]中推荐采用的垂直、水平接地极的接地电阻计算式(平均电位法)。由于不同电位算法采用了不同位置的电位,因此带来计算结果之间存在一定差异。规范[4-6]中垂直接地极计算式并没有计入其埋深的影响,而接地极埋深不同必然导致计算偏差;同时由于很多电力工程布置方式越来越复杂,导致其接地极的敷设条件不一定能满足公式的简化条件,也会给计算结果带来偏差,甚至是不正常结果。本文拟通过对以上各种偏差的分析,以便从实用的角度了解接地设计计算中所存在的问题,同时对不满足常规简化条件项目提供了推荐采用的新的接地电阻计算公式,并基于公式的变量组合分析,为接地网的敷设方式提供参考建议。
1 接地电阻计算公式
接地电阻是电流经接地极流入大地时接地极的电位和I的比值。对于一般圆钢接地极(如图1),经近似处理,设接地极长度为l,直径为d,当l≫d/2时,忽略接地极端部电场效应,则接地极附近空间任意一点N(rN,O,zN)的电位表达式为:
(1)
经积分可得:
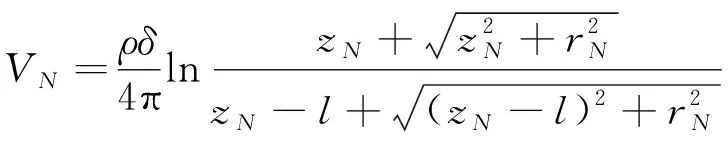
(2)
公式(1)式中:δ=I/l,即假定沿接地极轴线流散的电流密度是均匀分布的。
基于公式(2),采用中点电位法、平均电位法可以分别得到以下不同敷设条件时接地极接地电阻计算式如表1。

表1 接地极接地电阻计算公式
表1为接地体不同敷设方式时接地电阻不同算法的计算式,其中埋深为h的水平接地极接地电阻值通过计入互感影响R=R11+R12后得到,R11为接地极自电阻,R12为接地极互电阻。

表2 接地极自电阻、互电阻计算式
2 平均/中点电位法比值
如前所述,对于中点、平均电位法,前者采用的是接地极的中点电位,而后者采用的是接地极的平均电位,表1中中点电位与平均电位法的表达式显然存在不同,计算结果也会存在差异。下面拟通过算例进行简要分析。假定d=0.03 m,ρ=200 Ω·m,当接地极长度变化时,按不同敷设情况的接地极进行对比计算,计算结果见表3,其中比值为平均电位/中点电位法计算结果之比。

表3 全空间、半空间接地极公式简化前后对比 /Ω
表3中计算结果表明:
(1) 平均电位法计算结果低于中点电位法。接地极长度越短,中点、平均电位差距越大,电场分布更不均匀,平均/中点比值也就越小;接地极长度越长,此时平均电位、中点电位趋于靠近,端部电场影响减弱,比值越大。如半空间垂直接地极长度l=2.5 m,平均/中点比值为0.9477,即平均电位法结果低于中点电位法约5%;对于h=1 m水平接地极l=100 m和500 m时,比值分别为0.9533和0.9617。
(2) 全空间与半空间垂直接地极接地电阻值之间的差异,随接地极长度的增加而降低,l=2.5 m时,两者相差12%左右,平均法差别略大,说明对垂直接地极而言,全空间的敷设方式接地电阻降低不多,说明其埋深影响甚微。
(3) 对于水平接地极,接地极埋深h=1 m时,其与半空间敷设方式的接地电阻差异较大,l=2.5 m时达到接近80%,平均电位法差异同样略大,而其差异随着接地极长度的增加亦逐步减小。但无论如何,在埋深较浅时,埋深对水平接地极接地电阻值影响较大。
3 埋深为h垂直接地极接地电阻计算
前面公式(5)、(6)计算式为半空间垂直接地极接地电阻计算式,实际上一般垂直接地极均埋于地面以下1 m左右,与水平接地网位置基本一致,根据规范[7]及有关资料[3],当垂直接地极埋深为h时,其接地电阻计算式见表4。

表4 垂直接地极埋深为h接地电阻计算公式 /Ω
表4中各计算式的变量有接地极长度l及其直径d和埋深h。为便于对比分析,接地极长度分别为2.5、100及500 m,对应埋深为1、64、256 m,计算结果对比参见表5。
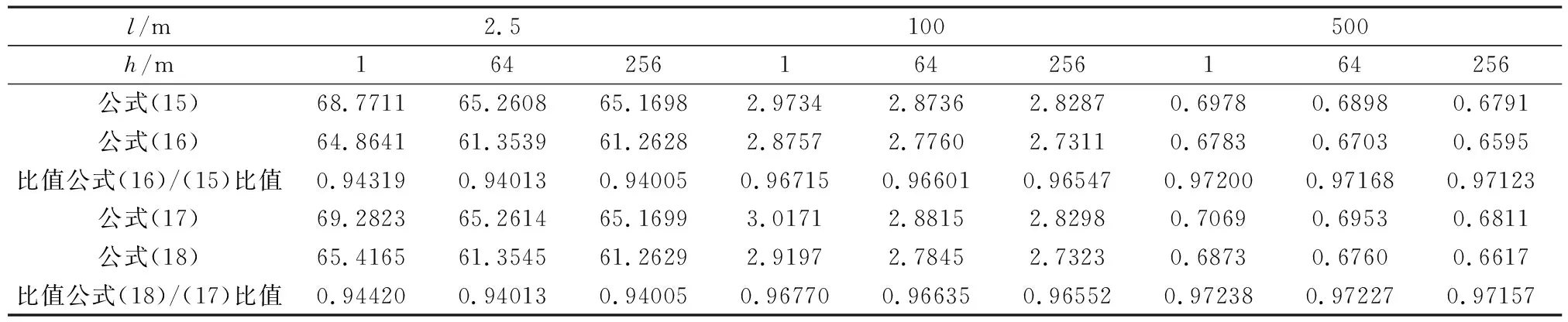
表5 顶端距地面h时垂直接地极接地电阻对比 /Ω
计算结果表明:
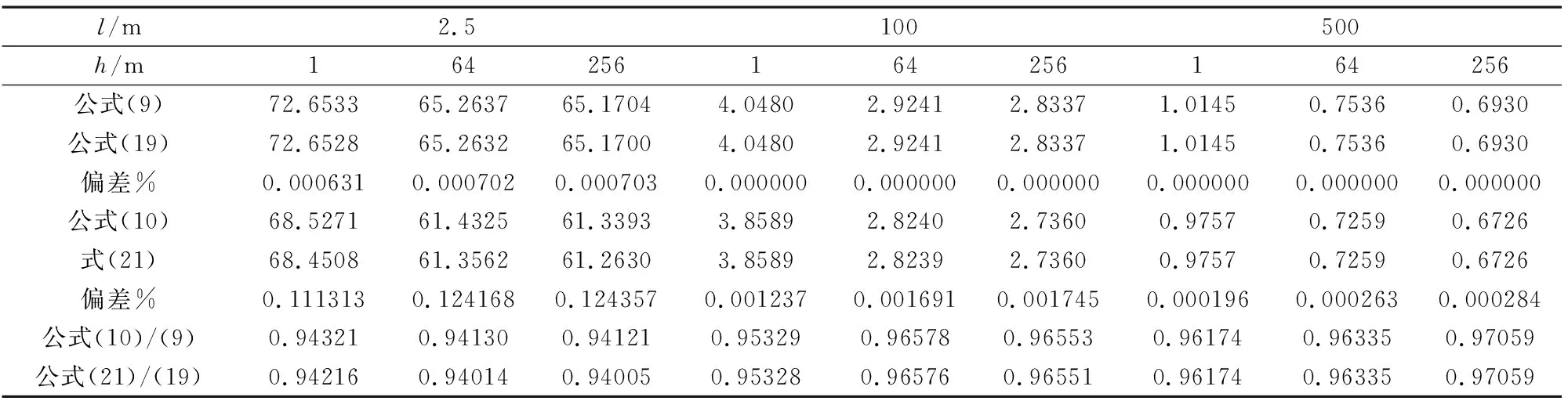
(1) 对于同一垂直接地极,处于全空间的接地电阻最小,而处于半空间中的接地电阻为最大值,距地面为h时则介于全空间与半空间之间。如l=2.5 m,接地电阻65.1393 Ω (2) 对应不同长度接地极,当接地极埋深变化时,接地电阻变化很小,即垂直接地极接地电阻对埋深并不敏感,但是接地极长度变化时,接地电阻变化明显。因此对于垂直接地极,增加接地极长度,降阻效果比增加埋深明显得多。 (3) 平均/中点比值计算也反映了上述特点,接地极长度或埋深变化时,平均电位法接地电阻值恒低于中点电位法,随着接地极长度增加,其比值将逐渐趋近于1.0,和前面全空间、半空间的比值变化特点基本一致。 同时对比表3中公式(5)、(6)结果与表5对应结果,其偏差计算参见表6。 表6 半空间垂直接地极与h=1 m接地电阻偏差 /Ω 从表6计算结果可以看出: (1)一般情况下垂直接地极长l=2.5 m,埋深在1 m左右,表6中埋深h=1 m的接地电阻值与公式(5)、(6)的计算结果偏差在6.330%~7.463%,与GB/T 50065附录A中编制说明计算偏差基本一致,同时,随着接地极长度的增加,两者的偏差越来越小。 (2)表6中所列偏差为半空间与h=1 m之间的偏差,如果叠加中点与平均电位法之间的计算偏差,其偏差则达到12.304%,对于一般工程设计该值偏高,可以认为规范[4]中附录A中A.0.1-1公式虽简单,但是计算结果偏大。 当接地极敷设条件l≫2h≫d/2成立时,表中公式(9)、(10)经简化可以得到以下各式,其中公式(20)为规范[4-7]中推荐采用的水平接地极工频接地电阻计算式。 中点电位法 (19) 平均电位法 (20) (21) 要使上面各式成立,接地极的长度应远大于其埋深2倍以上,接地电阻值计算才是满足要求的。但是对于埋深偏大的地下厂房,随着接地极埋深的增加,当l≫2h≫d/2条件不能成立,简化公式将不适合应用于工程设计计算。 如前所述,简化公式成立的前提是l≫2h≫d/2,当l≫2h不成立时,前述简化公式无法应用。为计算一般设计条件下埋深为h时的水平接地极接地电阻,下面按l≫d/2条件对公式(9)、(10)进行简化处理可得: 中点电位法 (22) 平均电位法 (23) 按表5设定条件对埋深为h水平接地极进行验证计算,参见表7。表7结果表明: 表7 按l≫d/2条件简化埋深h水平接地极接地电阻计算 /Ω (1) 埋深为h的水平接地极接地电阻计算式按l≫d/2进行简化后,和简化前计算公式相比,如埋深1 m时最大偏差远低于1%,其计算结果完全可以满足工程设计要求。 (2) 对于不同长度水平接地极,当埋深增加时,接地电阻变化比较缓慢,当埋深h趋近无穷大时,接地电阻趋近于全空间结果,即靠单纯增加埋深对降低接地电阻效果不大;而对某一埋深的水平接地极,当接地极长度变化时,其接地电阻变化明显,如长度由100 m变为500 m时,接地电阻约为原来的1/4。 (3) 对应表3计算结果,表7中埋深为h的水平接地极接地电阻值大于全空间接地极接地电阻,但小于半空间水平接地极接地电阻值,结果在合理区间。 全空间接地极、半空间垂直接地极与水平接地极接地电阻计算,其简化公式的应用条件是l≫d/2,目前规范中简化公式的计算精度均能满足一般工程设计要求,而对于埋深h的水平接地极接地电阻计算,当满足l≫2h≫d/2条件时计算结果满足工程设计要求,但是对于像埋深h较大的地下厂房的接地网,如采用一次求和法等计算水平接地极接地电阻时,需复核是否满足其公式简化条件,否则计算结果将可能完全失真,此时建议采用本文推荐公式(21)。 (1) 平均电位法计算结果低于中点电位法。接地极长度越短,中点、平均电位差距越大,两种算法的差距越大;接地极长度越长,两者差距越小。 (2) 垂直接地极的埋深对其接地电阻值影响不太敏感,接地极长度的增加更有利于降低接地电阻值;但在埋深较浅时,埋深对水平接地极接地电阻值影响很敏感,水平接地极敷设时适当增大埋深有利于降低接地电阻值。 (3) 基于接地极理想模型推演得到的各类计算公式,当满足l≫2h≫d/2简化条件时,简化公式计算结果和精确表达式相比偏差较小,其中也包括目前规范中垂直及水平接地极接地电阻计算公式。 (4) 实际工程中,尤其对于地下工程,简化条件不满足时,埋深h的水平接地极接地电阻计算,此时无论平均电位法还是中点电位法,其接地电阻计算结果出现不合理情况而无法应用。本文推荐采用本文提出的公式(21),计算偏差很小。 (5) 计算结果表明,无论垂直接地极还是水平接地极,其接地电阻对于其埋深均不敏感,埋深增加对接地电阻降低效果有限,因此接地极布置时不必刻意增加埋深;而当接地极长度增加时,两者的接地电阻降低效果更好。
4 埋深h水平接地极推荐计算公式
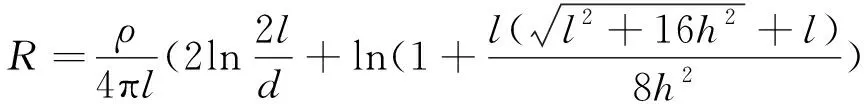
5 结 论

