通感一体化系统的下行功率分配技术*

赵喆，夏树强，马一华，韩志强，杨立，孟骁

（1.中兴通讯股份有限公司，广东 深圳 518057；2.移动网络和移动多媒体技术国家重点实验室，广东 深圳 518057；3.上海中兴软件有限责任公司，上海 201203；4.南方科技大学，广东 深圳 518055）

0 引言

移动通信系统每隔十年演进一代，已经从第一代（1G）演进到第五代（5G）。移动通信网络逐渐从ToC 服务领域拓展到ToB 领域，已经从只关注数据传输速率拓展到和更多垂直行业的融合和服务[1]。随着5G 网络全球大规模部署，业界已经开始探索更多的垂直行业应用以及如何支持不断涌现的新场景用例业务。第三代合作伙伴项目3GPP 5G-Advanced[2-3]已经开始了通感融合方面的研究，重点关注相关的场景用例、技术需求等[4-5]。面向未来的6G 新系统网络，业界已经在6G 愿景和关键使能技术展开讨论并逐渐形成统一的认识。从目前各国或各个标准组织发布的6G 白皮书看[6-9]，通信感知一体化技术将是其中一个重要的使能技术。

面向5G-Advanced 演进系统和未来6G 移动新系统，无线感知相关能力和服务的价值意义被业界越来越重视和提升利用。为此，学术界和工业界都已针对“通感一体化”（或称“通感融合”）方面，开展了大量的理论预研[10-11]和工程原型验证[12-14]。5G-Advanced 基于现有5G 网络架构，不对系统架构重大更改，只对现有功能进行适当修改，并引入基本的传感功能。6G 将从系统设计一开始，就原生地考虑更丰富的感知功能，将感知功能视为网络的基本能力，因此6G 新网络将在更多制式、频带和感知方法的基础上，实现支持更强大的感知能力和更好的感知性能[15]。5G-Advanced 支持的感知和6G 支持的感知主要特点区别如表1 所示：

表1 5G-Advanced与6G支持的感知特点区别

在国内，以IMT-2020 推进组为代表，基于当前5G-A 演进系统，已进行了多项通感融合场景用例方面的可行性验证测试[16]；同时，以IMT-2030 推进组为代表，面向未来6G 移动新系统，也在积极开展更全面综合原生的通感融合体系架构设计和关键技术研究[17]。随着未来网络云原生、端到端切片化[18]、底层物理资源和上层逻辑功能解耦[19]等新设计理念的深入应用，在通感一体化系统中，通信感知业务操作共享复用相同的时间、频率、功率等资源且通感业务功能之间在上层紧密协同，将会受到业界越来越多的重视和开发。

通过物理层频谱和功率资源的最大化复用共享，能够实现移动系统资源利用率的提升和通感业务性能价值等方面的拓展倍增。面向公共的频谱和功率资源池，如何权衡折中通信感知业务性能，是通感一体化系统中的一个重要研究问题。在信号特性方面，由于OFDM 波形在频谱效率、干扰抑制、与MIMO 技术良好适配结合等方面的显著优势，因此已在4G/5G 移动系统得到广泛应用。此外，由于OFDM 信号的模糊函数呈现单一尖峰形状，具有良好的距离分辨率特性，因此也能很好地去承担无线感知任务。基于上述两个原因，通感一体化融合波形设计中，经常还是以OFDM 作为主要调制方式。文献[20]将多个OFDM 符号作为一个一体化信号，通过调节多个符号的相位来优化OFDM 的模糊函数，通过对OFDM 符号整体加载相位调制来携带通信信息。文献[21] 提出一种功率资源分配机制，在保障雷达接收信干噪比的前提下，最大化通信端的吞吐量，或者在保证通信吞吐量的同时，最大化雷达接收信干噪比。文献[22] 以目标参数估计的克拉美罗和通信信道容量为衡量指标来对子载波的功率分配进行了优化。文献[23] 对闲置的时频资源进行填充，并通过对填充的符号的设计优化OFDM 信号的感知效果。这种使用闲置时频资源的方法存在两个主要问题：（1）必须要有足够多的闲置时频资源才能得到较好的感知功能优化效果；（2）分配在闲置资源上的功率对通信功能性能没有帮助。

本文将以OFDM 作为通信感知一体化候选波形，对在不同的资源调度策略下，发射功率分配对有效相关带宽/ 距离分辨率的影响进行深入分析。在此基础上，提出了一种以通信功能和感知功能的折中性能为指标的最优发射功率分配方案。

1 通感单独优化的功率分配技术

1.1 系统模型

图1 给出了本文讨论的通感一体化系统模型示意图，系统中包括1 个通感一体化基站，该基站向K个通信用户设备（UE,Ueser Equipment）发送下行数据，并处理接收对象反射回波以完成感知任务。发射信号采用OFDM 信号，包含N个子载波，子载波带宽为Δf，其基带表达s(t)为：

图1 通感一体化系统系统模型

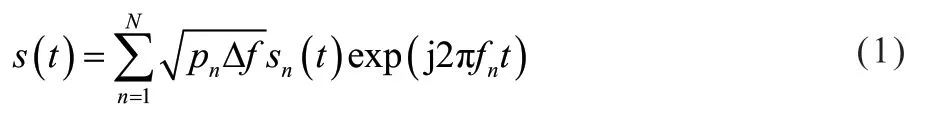
其中，pn、sn和fn分别为第n个子载波的发射功率谱密度、调制符号和载波频率。

1.2 针对感知的功率分配技术

设发射信号的带宽B，且所有频点的回波信号均可用于感知，则系统的名义分辨率定义为c/2B，其中c为光速。然而，名义分辨率只考虑了感知信号主瓣内邻近目标的分辨能力，没有考虑旁瓣干扰对目标分辨的影响。因此，为了更为精准地刻画旁瓣干扰对目标分辨的影响，本文使用感知信号的有效相干带宽Beff对应的距离分辨率c/Beff来衡量感知性能。当发射信号为s(t)时，Beff可以用如下形式表示[24]：

其中，S(f)为发射信号s(t)的傅里叶变换，χ(τ)为感知信号s(t)的距离模糊函数。从时域看，Beff表征了距离模糊函数与冲击函数（理想模糊函数）相似程度，从频域看，Beff表征了距离模糊函数的频谱函数与均匀谱的相似程度。

对于OFDM 波形，设系统在带宽为B、子载波个数为N的条件下，可用的最大功率谱密度之和为A，即，Beff可以进一步表述为：

接下来具体分析一个包含两个UE 的系统，两个UE分别记为UE1和UE2，设系统共有800 个可用子载波，子载波间隔为120 kHz，则总带宽为96 MHz。按照频率顺序，这些子载波索引为1,2,...,800，并将其均分给两个UE，各自分配的子载波索引分别为[1,400]和[401,800]。设UE1和和UE2均采用QPSK 调制，使用点数为8 192 的IFFT 进行过采样。关于UE1和UE2，图2 给出了两个UE在功率比分别为0 dB、3 dB、6 dB、9 dB、12 dB 和15 dB时OFDM 波形的距离模糊函数在主瓣附近的示意图。

如图2 所示，OFDM 波形的距离分辨能力对功率分配具有敏感性。具体而言，当两个UE 的功率比值为3 dB 时，第1 副瓣已经很不明显，超过3 dB 时，0 dB 时的第1 主瓣和第1 副瓣合并为一个更宽的主瓣。在上述仿真中，带宽B为96 MHz，按照名义分辨率，其可以区分同方向c/2B=1.562 5 m 内的两个目标，但是根据图1 可以看出，当UE1 和UE2 的功率比超过3 dB 时，如果两个目标的距离为1.562 5 m，接收机实际上是无法区分的，其只可以区分同方向不小于3.125 m 的两个目标。进一步地，从图2 可以看出，随着两个UE 分配功率比值的增加，副瓣也有逐渐升高的趋势，这说明：在基于OFDM 波形的通感一体化系统中，不恰当的功率分配不但会降低距离分辨率，对距离精度也会有不利影响。

图2 OFDM波形的距离模糊函数

1.3 针对通信的功率分配技术

设每个UE 被分配的带宽相同，且每个UE 的分配带宽内各子载波功率相同，则各用户的功率谱密度满足以下关系：

其中，P为最大发射功率，pk为UEk的发射功率谱密度。进一步记UEk信道增益为hk，接收端噪声功率为δ2，该系统的信道容量为：

pk的分配依赖基站调度时所采用的功率分配策略。当基站不利用UE 的信道状态信息（CSI,Channel State Information）时，系统采用等功率分配最佳，此时速率上界为。而当基站利用UE 的CSI 时，从通信角度，理论上按照注水定理的方式进行功率分配以获得最佳容量，此时pk的分配如式(6) 所示：

其中，q为注水功率门限。此时系统可以获得的最佳容量上界为：

在上述假设下，基站发送上述信号的在感知角度有效信道带宽可以重写为：

根据前面的分析，当系统按照无CSI 进行通信发送功率分配时，发送信号的有效相关带宽最大，从感知角度这样分配功率也是最佳的。而当基站端利用CSI 时，发送功率的分配依赖于各UE 的信道增益，此时虽然通信侧的信道容量最大，但是感知侧的距离分辨力未必最优，尤其是各用户间信道增益差别较大时。综上所述，在通感一体化系统中，设计一种能够综合考虑通信和感知性能的联合评价指标，并据此设计一种新的功率分配机制是非常必要的。

2 面向通感一体化的联合功率分配技术

本文从资源利用率出发设计面向通感一体化的评价函数。对于通信功能来说，可以使用实际信道容量与最大信道容量的比值表示资源利用率。而对于感知功能来说，可以使用感知的有效带宽与资源带宽的比值表示资源利用率。为了进行通信性能和感知性能的良好折中，本文联合这两种资源利用率提出了一种通感一体化资源利用率的评价函数：

其中，p=[p1,p2,...,pK]T为各用户功率分配值组成的矢量，η∈[0,1] 为可调的通感权重参数。当η越接近于1，资源利用率的评价函数f(x)越侧重于通信利用率；当η越接近于0，资源利用率的评价函数f(x)越侧重于感知利用率。

可以对式(10) 中的资源利用率评价函数进行优化，构建如下的最小化问题：

求解这个最小化问题，则可得到面向通感一体化的联合功率分配。但是在此问题中，等效带宽Beff相对于变量pk是非凸（non-convex）的，这就导致了此优化问题难以求解，无法获得最优的功率分配。

式(10) 不是凸优化的主要问题，是等效带宽的相反数-Beff相对于pk非凸，为了解决优化目标非凸的问题，本文将等效带宽Beff重写为：

同时，通过引入两个松弛变量α和β，原优化问题可以被转化为如下形式：

在该问题中，目标函数为仿射函数，显然为凸函数，h(p,α,β)与g1(p,α,β)的约束同样为线性约束。但是g2(p,α,β)中包含了优化变量的非二次型乘积项，是一个非凸约束，因此该问题同样无法直接求解。通过观察非凸项可以发现，非凸约束仅存在于β与p之间，通过使用交替优化法（AO,Alternating Optimization）即可解决该问题。具体来说，在第k次优化迭代过程中，先固定β为β*k-1，求解p和α的优化问题，得到p*k和α*k，然后固定p和α为p*k和α*k，求解β的优化问题。这两个子优化问题均为凸问题，因而该算法必然至少收敛到一个局部最优点。

3 仿真结果

系统仿真采用标准的OFDM 波形，仿真参数设定如表2 所示。带宽B对应的距离分辨率为1.736 m，然而在实际中，由于发射OFDM 波形的非理想性，导致各个子载波之前存在功率差异，使得等效带宽大大减小，无法获得理想分辨率，因此需要联合考虑感知和通信的资源利用率，来优化通感一体化的功率分配。仿真中假设用户之间平均分配带宽资源，单个用户是平坦衰落且采用恒模的调制方式。该方案中除OFDM 波形外，其他参数均可推广至任意其他值以应对不同的通信、感知场景。在仿真中，用户分布和对应的信道随机生成，使用了1 000 次仿真的结果进行平均，以获得准确的仿真结果。

表2 仿真参数设定

如图3 所示，采用不同的通感权重参数η可以得到不同的功率分配结果。当η=0 时，只对感知资源利用率进行优化，对应的是等分功率分配的结果；当η=1 时，只对通信资源利用率进行优化，对应的是注水法的功率分配的结果。从图中可以看出，随着权重参数更加偏向于通信，通信资源利用率先缓慢增加，再快速增加，最后缓慢增加趋于定值，同时，感知资源利用先缓慢下降，再急遽下降，最后趋于定值。图4 展示了通信资源利用率和感知资源利用率互相的折中关系。通信资源利用率最低的点对应着等分功率分配的结果，如果要提高通信资源利用率，则需要牺牲感知资源利用率。同时，在曲线的左侧，可以通过感知资源利用率的极小下降来换取通信资源利用率的提升。然而随着通信资源利用率的升高，则需要舍弃大量的感知资源利用率来进一步提升通信资源利用率。

图3 通信功能和感知功能的资源利用率随权重参数η的变化曲线

图4 通信资源利用率和感知资源利用率互相的折中关系

图5 展示了在特定通感权重约束条件下，功率联合分配方案相比于传统方案的性能对比。本文讨论两种约束，第一种是η=0.5，此时将两种功能的资源利用率带有相等权重；另一种是限制两种功能资源利用率相等，此时可以通过选取特定的η来实现，也可以通过限定α=β来实现，本仿真采用的是后者。对于η=0.5 的所提的联合功率分配，此时取得的通信资源利用率为70.8%，感知资源利用率为96.5%。相比于平均功率分配通信资源利用提升了超过10%，而感知资源利用率只牺牲了3.5%；相比于注水法的功率分配，通过牺牲30%的通信资源利用率，实现了感知资源利用率翻倍。对于α=β的所提的联合功率分配，此时取得两种功能的资源利用率均为81.0%，此时对应的η＞0.5，通信资源利用率获得了更高的权重，因此相比于η=0.5，提升了通信资源利用率。此时，该方案相比于传统方案获得了更加均衡的通信和感知性能。所提方案的两种设置中，前者注重通感一体化整体的资源利用率，后者注重两种功能之间的公平性，可以适用于不同的通感一体化场景。

图5 所提出的联合功率分配和传统方案的对比

4 结束语

本文聚焦在通信和感知共享完全相同的时频和功率资源时的下行功率分配机制。通过深入探讨在通信最优和感知最优的功率分配方案下感知性能和通信性能的变化，本文提出了一种以通信速率和有效感知分辨率为权衡目标的效能评价方案。在该评价方案下，在权衡因子任意给定时，均可得到一个至少局部最优的功率分配方案。仿真结果表明，通信和感知性能的权衡具有非线性性。通过合理的调整权衡因子，可以在牺牲少量的感知（或通信）的性能的条件下，换来通信（或感知）性能的大幅度提升。

作为系列研究的第一步，本文重点考虑了单基站模式下多UE 等带宽时的最佳功率分配机制，未来我们还将考虑不同UE 在业务上的差异，为UE 分配不同带宽时通信感知联合功率分配机制，并将研究进一步拓展到多基站的实际蜂窝环境。