子序列决策聚类下的光伏系统工况判别

潘杰男，刘光宇，朱 凌

(1.杭州电子科技大学自动化学院，浙江 杭州 310018；2.浙江财经大学信息管理与人工智能学院，浙江 杭州 310018)

0 引 言

近年来，光伏电站运行工况的故障诊断一般采用无监督学习方法[1]，解决了光伏电站工况数据异常样本筛选困难的问题。一天获取的光伏发电数据可能存在多种运行状态，对于高维时间序列数据运行工况的判别，文献[2]将获取到的光伏发电数据作为静态数据，直接使用聚类算法进行故障诊断，没有考虑样本点在时间维度上的分布特性；文献[3]将时间序列数据的聚类分为全时间序列聚类和子序列时间序列聚类，后者又称为子序列聚类，并利用固定的窗口对整段时间序列数据进行逐个分析，不能解决时间间隔不规则的数据；文献[4]指出全时间序列聚类算法的难点在于线段长度的选取，提出一种针对光伏时间序列数据的在线故障诊断方法，避免了序列的分割问题；文献[5]先将时间序列数据分割成多个相对较短的时间序列样本集，每个样本表示一天的发电数据，然后进行多种聚类算法，成功获得光伏发电数据的中心序列，但在文献[5]中，人为分割的依据是仪器的采样时间，存在一定的先验知识，而且将一天中所有数据点作为一个样本，子序列可能存在多种运行状态，无法进一步得到多种具体工况的分类；文献[6]指出，子序列聚类往往先采用滑动窗口提取多个子序列，再对子序列进行聚类，窗口的大小直接影响算法的性能。窗口太大，忽略了某些数据点的重要状态信息；窗口太小，则耗费大量时间。为了获得每个数据元素的标签，文献[7]将时间序列的每个元素都分配到包含它的子序列的多数标签上，但其描述的决策方式可能产生冲突，如果某样本点同时属于2段子序列，而这2段子序列被聚类判别为不同类别，需对该点的类别进行计数决策，遇到计数相等时，该点的类别将无法进行合理判别。为了得到类簇信息与真实光伏发电系统工况相近的数据，本文通过步长和大小均可变的滑动窗口提取多条子序列，再对重叠子序列进行决策，提出一种子序列决策聚类(Subsequence Decision Clustering, SDC)算法，对光伏系统的时间序列数据进行工况判别。

1 符号定义

为了便于理解光伏发电系统运行工况和本文聚类方法的描述，给出相关的符号、名词与定义，如表1所示。

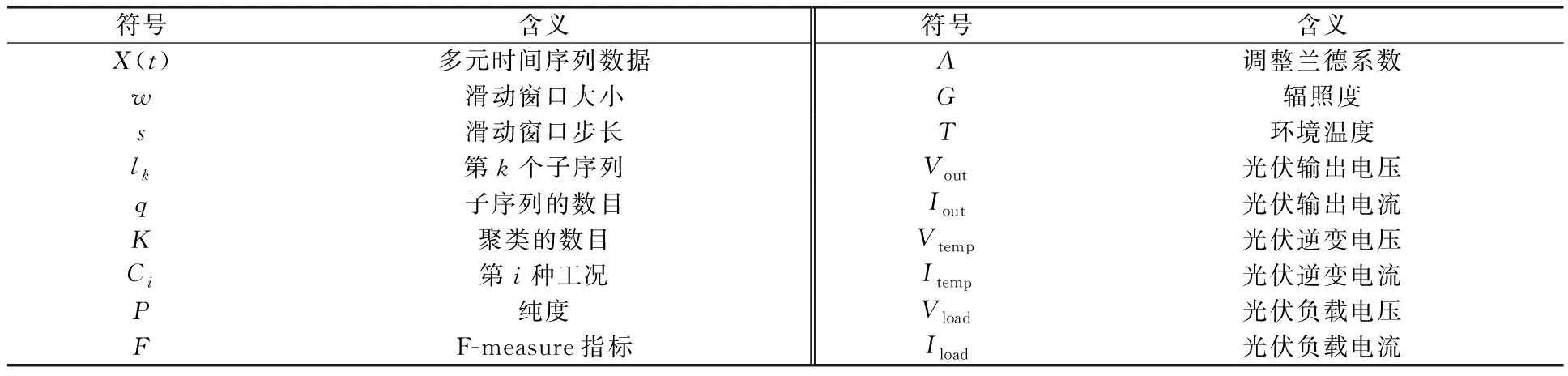
表1 相关的符号说明

2 子序列决策聚类算法

针对一条多工况的光伏时间序列数据，为了充分利用样本点在时间上的关联性，本文提出一种子序列决策聚类算法SDC，根据可变步长和大小的滑动窗口提取多条子序列，对子序列进行层次链接聚类，比较分析各子序列的多类别重叠区域的特征数据平均值，通过标签决策得到最终标签，算法流程如图1所示。

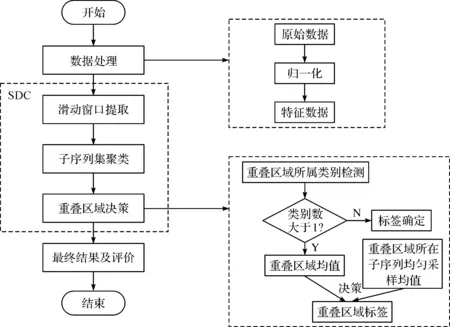
图1 子序列决策聚类算法流程

2.1 数据归一化

进行聚类分析前，往往需要对原始数据进行归一化处理，得到利于算法分析的特征数据。从光伏电站采集到的原始数据一般包括光伏电池板的辐照度、温度、输入输出电压、电流及其他内外部数据等多维数据，不同维度数据的单位不同，数值变化也不同，可采用数据变化的方式来消除这些差异。数据变化方式主要有min-max归一化和z-score归一化。对第i维，第j个样本的min-max归一化和z-score归一化分别如下：

(1)

(2)

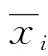
2.2 聚类过程

经过归一化处理得到的特征数据仍拥有时间维度上的信息，直接将其载入到聚类算法进行模式判别时，依然会丢失数据点之间时间上的关联性。为此，本文使用SDC算法进行数据的决策聚类，得到最后的聚类结果。算法的主要步骤如下。

(1)提取新的子序列样本集。设置一个长度为w，步长为s的可变滑动窗口(w>s+1)对多元时间序列进行提取，得到新的子序列样本集

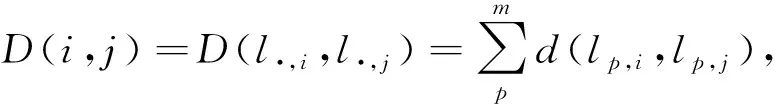
(3)检测重叠区域的类别。子序列包含多个样本点，相同样本点存在多种类别，将子序列重叠的区域分为O(k)={Oc(k)|k=1,2,…,m}[8]，其中k表示重叠区域的序号，c表示重叠区域所属子序列样本集被划分的所有类别。如果c的数量只有一类，则无需决策；如果大于一类，则需决策该重叠区域的所属类别。

(4)决策重叠区域的所属类别。将重叠区域所属的子序列样本集分为多类，对每个样本集进行均匀采样，采样数量为当前重叠区域所含原样本点数，如果重叠区域过长，则分段决策，每段长度为步长s。分别求采样集合和待决策重叠区域的平均值，将重叠区域所含数据点的类别决策为均值与该重叠区域均值最相近的样本的类别。

2.3 最终结果及评价

时间序列的每个时间样本点都得到类别标签后，从2个方面来评估聚类算法的聚类质量，一是通过对得到的结果进行反归一化，得到各维度的类簇信息，计算各个类簇信息的均值，并与真实工况下均值进行比较，两者的差异用相对误差来表示；二是通过一系列外部评价指标[9]来评价聚类质量，本文选取3个较为常见的指标，分别为F-指标(F)、纯度(P)、调整兰德系数(A)。

3 仿真实验与分析

首先，采用本文提出的SDC算法和文献[10]采用的层次聚类算法对采集到的相同光伏发电时间序列数据进行聚类仿真，并与真实工况进行对比；然后，比较分析当前常用的层次聚类[10]、密度峰值聚类[11]、k-均值聚类[12]及本文算法的聚类外部评价指标。

3.1 实验数据采集及归一化

将自制的微型光伏发电系统置于晴朗的室外，在不同时间段设置4种工况，分别为正常(C1)、开路故障(C2)、全部遮阳(C3)、部分遮阳(C4)。对系统依次设置6段真实工况，分别为C1，C2，C1，C3，C1，C4，具体数据采集情况如表2所示。采集到光伏系统的原始数据X(t)∈R8×1 791，8个维度的数据分别为环境温度T、辐照度G、光伏输出电压Vout、输出电流Iout、逆变电压Vtemp、逆变电流Itemp、负载电压Vload、负载电流Iload，各个维度数据在6段真实工况的呈现如图2所示。

表2 不同工况的数据采集说明

图2 不同工况下，各维度原始数据

根据图2的原始数据，在不同聚类数目K下，分别采用max-min归一化和z-score归一化进行数据转换，得到的卡林斯基-哈拉巴斯指标(Calinski Harabasz，CH)[13]如图3所示。

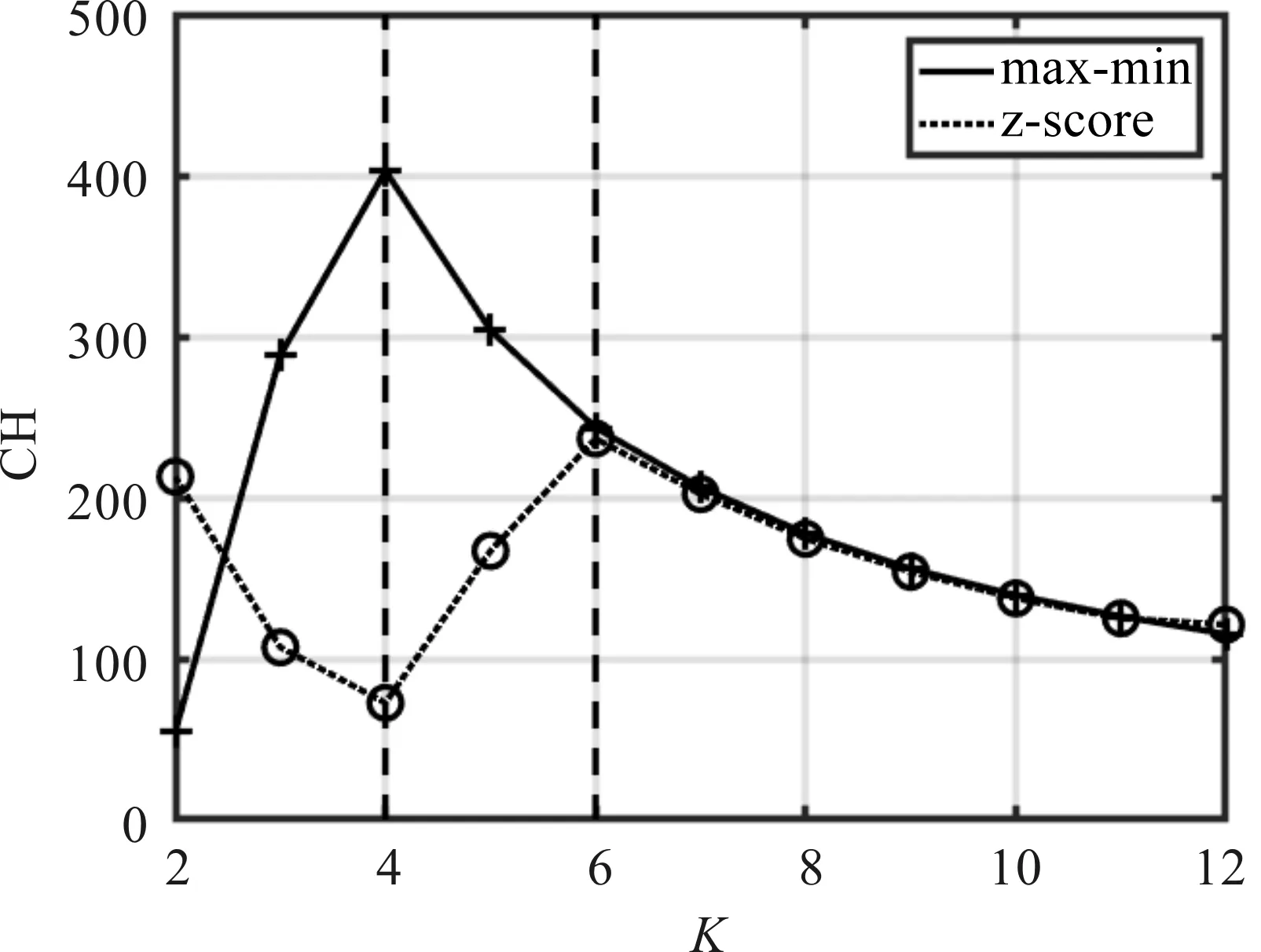
图3 不同聚类数目下，数据归一化的CH指标

图3中，CH值越大表示聚类数目更优[13]，因此，本文选择min-max归一化进行仿真实验。

3.2 子序列决策聚类结果与分析

采用w=400,s=200的滑动窗口对归一化后的数据进行提取，得到新的子序列样本集，由式(1)可以得到此对参数下子序列个数q=8，对8段子序列进行层次聚类。实验中，序列之间的相似度计算采用文献[14]的针对不等长序列之间的欧式距离，链接方式为文献[15]的平均链接，得到聚类树和对应子序列所属类簇的决策如图4所示。

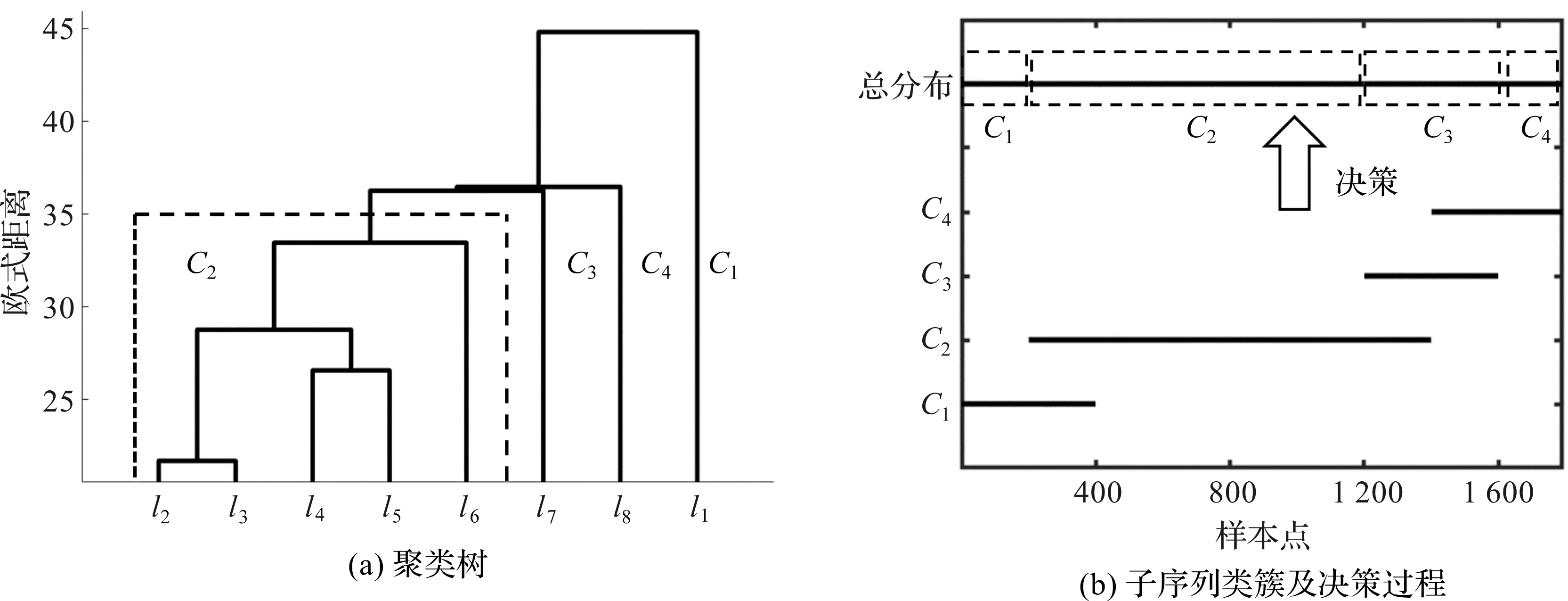
图4 聚类树及标签决策过程

由图4(a)可以看出，当子序列样本集被分为4类时，子序列2～6归为一类，其他3个子序列各为一类。当标签完成决策后，得到如图4(b)所示的标签分布。通过计算得到不同工况下每个维度各类簇的均值与真实工况的均值如表3所示。

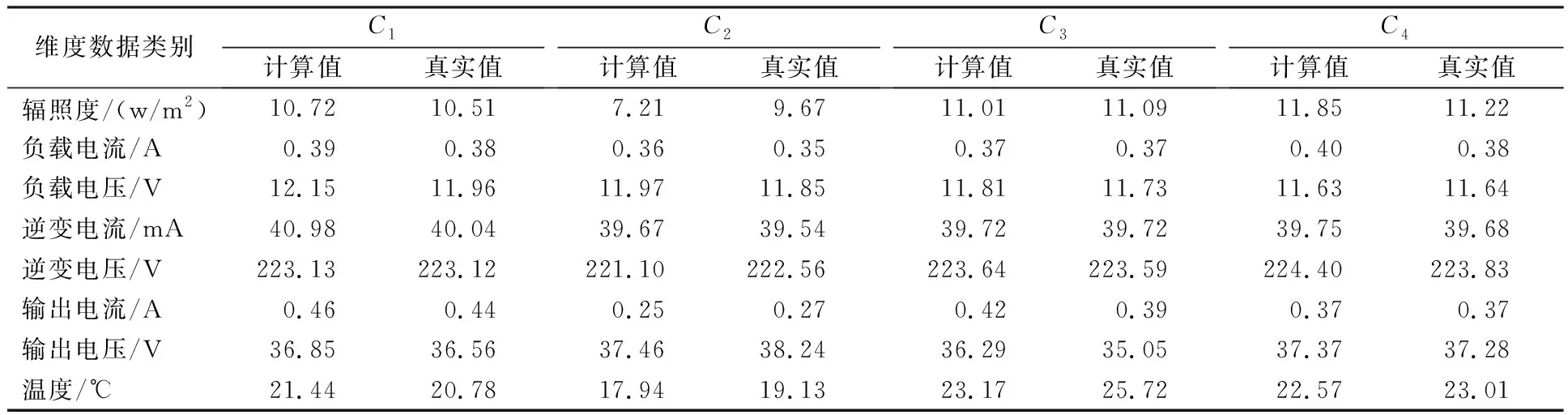
表3 不同工况下，各维度类簇均值与真实工况的比较

3.3 不同聚类算法的判别结果

为了比较各个维度数据在各个工况下相对误差的准确性，分别采用本文算法、与文献[13]相同归一化处理后的层次聚类算法进行工况判别，得到4个类簇各维度的均值与真实工况的相对误差如表4所示，其中的误差1，误差2，误差3，误差4分别表示算法得到的4个类簇与4种真实工况的相对误差。

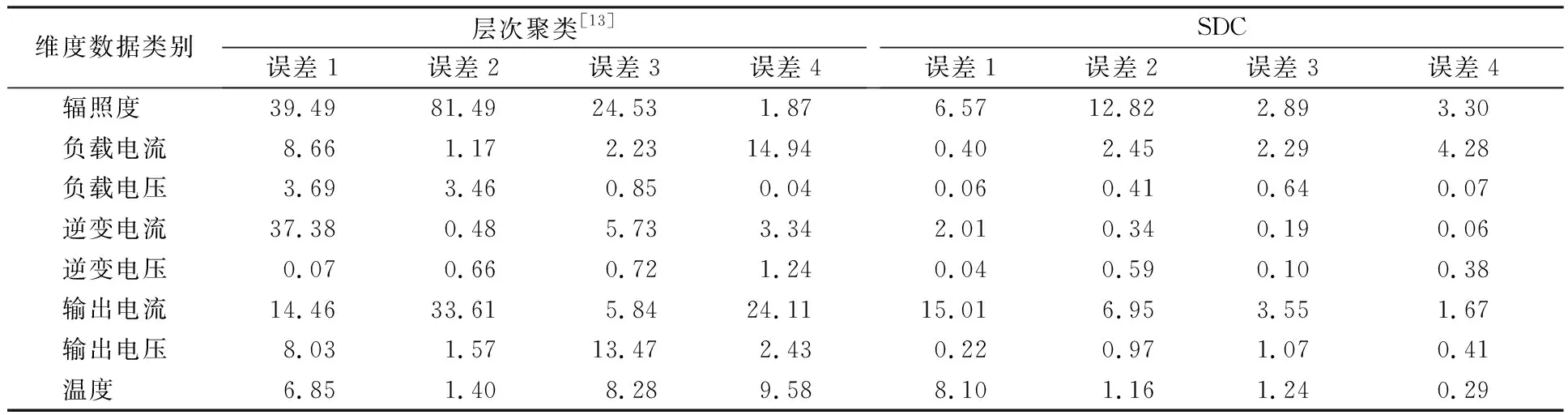
表4 不同工况下，不同聚类算法各维度数据与真实工况的相对误差 单位：%

从表4可以看出，SDC算法得到的误差结果中，相对误差最高的是输出电流这一维度数据的误差1为15.01%，其余31组均在15%以下；层次聚类算法得到的结果中，辐照度这一维度数据的误差2高达81.49%，同时其他大部分相对误差也高于SDC算法；在27组数据中，本文提出的SDC算法均小于层次聚类算法，得到的类簇更接近真实工况。

聚类的质量往往通过聚类的外部评价指标进行衡量，外部评价指标和相对误差在一定程度上呈正相关。将文献[10]的层次聚类算法、文献[11]的密度峰值聚类算法、文献[12]的k-均值算法和SDC算法的外部评价指标进行比较，结果如表5所示。

表5 不同算法的外部评价指标

由表5可以看出，SDC算法的3个外部评价指标都要高于层次聚类算法和密度峰值聚类算法，说明SDC算法的聚类质量要优于这2种算法。在A指标上，k-均值聚类算法要高于SDC算法，但在F和P指标下，SDC算法优于k-均值算法。

实验中，SDC算法将样本集的结果标签分成4段，虽然与真实工况的6段不一致，但在没有先验知识的情况下，和层次聚类算法相比，SDC算法得到的相对误差更小。在与层次聚类算法、密度峰值聚类算法、k-均值算法的外部评价指标对比中，SDC算法除了A指标小于k-均值算法外，F和P指标均为最大。所以，SDC算法得到的类簇更趋近于真实工况，其聚类质量指标有较大优势，在本次光伏时间序列数据的工况分析实验中取得更理想的结果。

4 结束语

本文主要研究光伏时间序列数据的工况分析，提出一种子序列决策聚类算法。既克服了普通层次聚类在时间序列聚类上的弱点，又改进了子序列聚类标签决策过程，得到的类簇信息与真实工况的差异不大，实现了对光伏发电时间序列数据的工况判别。但是，本文通过实验得到的聚类为4段，真实工况为6段，可能是选取的2个滑动窗口参数引起的。后续将针对窗口大小以及窗口步长的选择展开进一步研究，选择最优参数，从而得到更好的聚类结果。