基于博弈论组合赋权的洪水风险评价——以武威地区为例

苏广全， 吕海深， 朱永华， 陈庭兴， 花佳程

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098；2.河海大学水文水资源学院，江苏南京 210098）

洪水灾害是世界发生最为频繁的自然灾害［1］。随着气候变化及城市化进程的加速，中国成为百年内世界上洪水风险增长最显著的地区［2］。洪水风险评估作为洪水风险管理的重要工具，对防洪减灾工作具有重要的实际应用价值，可以提高公众对洪水风险的意识。

20世纪以来，各国开展了大量的洪水风险评估研究，形成以下3种洪水风险评估方法：（1）基于历史数据［3-5］，结合机器学习或统计方法来确定洪水风险薄弱区；（2）构建评价指标体系进行洪水风险分析［6-8］；（3）采用雷达遥感数据或二维水动力模型进行洪水淹没情景分析［9-11］。这些广泛应用的洪水风险分析方法仍存在一些不足：如基于历史资料进行风险分析的方法无法准确反映洪水的空间变异性；构建评价指标体系的方法往往在指标赋权上存在主观性；采用雷达遥感和水动力模型的方法需要大量的数据，且不考虑承灾体和致灾环境对洪水风险的影响［12］。

洪水风险评估需要综合多种要素来确定洪水风险，各要素与最终洪水风险之间的关系具有模糊性和随机性。因此，考虑模糊关系的模糊综合评价模型广泛应用于风险评价［13］。模糊综合评价模型中最重要的问题就是指标权重的确定，以往研究多采用单一赋权方法，如AHP（analytic hierarchy process）法、德尔菲法等主观赋权方法［6,8,14］，CRITIC法、熵权法等客观赋权方法［6,13］。然而，主观赋权方法严重依赖专家的主观经验，客观赋权方法仅依靠数据计算权重，不考虑评价因素对评价主体的重要性，得到结果往往与实际情况存在较大差异。为减少赋权主观性，并兼顾决策者经验，结合主客观赋权的博弈论组合赋权方法被提出，以期得到更为符合实际情况的赋权结果［15］。

近年来，气候变化导致水循环加速，极端气象事件频发，干旱区、半干旱区的洪水风险评价研究得到关注，但研究尺度多为省一级［4-5,16］，没有对洪水风险脆弱区进一步细化，且研究多侧重于洪水危险性，缺乏对洪水易损性的考虑。甘肃省武威市环境气候复杂多变，南部祁连山植被覆盖度高，河网密集，降雨频繁，是甘肃省中部的暴雨中心之一，受到山脉融雪影响，春季洪水时有发生［17］；北部为荒漠区，降雨稀少，植被稀疏。受到区域南部多山地形和沙漠地区气候的影响，武威市洪水灾害频率极高，根据历史资料，1971—2012 年武威市仅山洪灾害平均每年发生11 次［18］。2006 年7 月底凉州区西营镇山区每小时降水超80 mm，产生泥石流造成了严重的人员伤亡以及经济损失；2011年8 月14—18日凉州、古浪、天祝3 县区产生洪涝致10.74×104人受灾。研究表明，武威市近年山区降水有所增加，洪水频率呈现增长趋势［19］。

该研究基于GIS 技术，通过对武威市的暴雨次数、归一化植被指数、高程标准差、人口密度等因子的综合分析，并采取博弈论组合赋权方法构建洪水风险评价模型。将AHP 法和熵权法与博弈论组合赋权法进行比较，验证所提出的方法对洪水风险管理的有效性，对结果进行合理性分析，对武威市洪水风险进行评估和分区，为武威市的洪水预报、预警、防控提供合理依据。

1 研究区概况与方法

1.1 研究区概况

武威地区位于甘肃省中部，地理位置为36°29′～39°27′N，101°49′～104°16′E，总面积32345 km2，是黄土高原、青藏高原和蒙新高原的交汇处（图1）。南接祁连山脉，中部为河西走廊平原，北交腾格里和巴丹吉林两大沙漠，海拔在1200～4700 m间，由南至北高程逐渐降低。年均降雨量在100～600 mm，降雨集中在6—9月，8月最多，降雨量呈现由南向北减少的趋势。区域内蒸发强烈，空气干燥。流经的主要河流为黄河和石羊河，其中石羊河发源于祁连山脉东段，上游由西营河、黄羊河和西大河等河流组成，下游内流入民勤县的沙漠盆地，流域面积3.98×104km2。

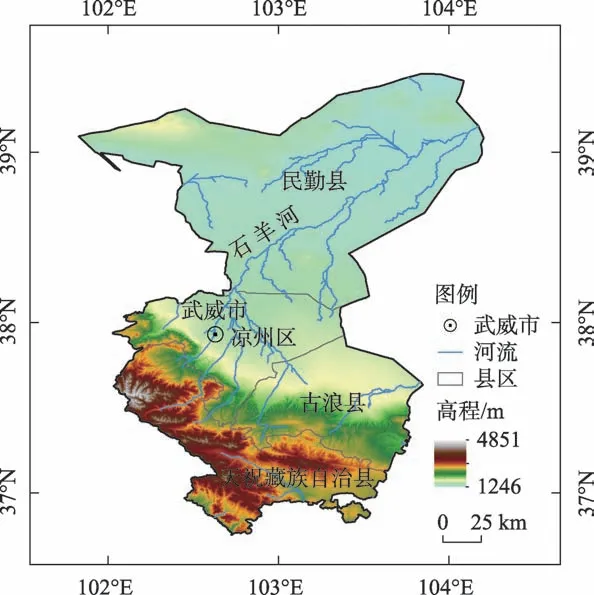
图1 研究区概况Fig.1 Overview of study area

1.2 研究方法

首先，根据灾害理论［20］及武威自然环境和社会经济特征，按照致灾因子危害性、孕灾环境稳定性、承灾体脆弱性3个方面选取了7个指标作为洪水风险评价要素：第一步，构建洪水风险评价指标体系；第二步，通过GIS技术对指标预处理，分别选取熵权法与层次分析法计算客观权重与主观权重，采用博弈论进行组合赋权；第三步，根据博弈论组合赋权得到各指标组合权重，采用模糊综合评价方法构建武威洪水风险评价模型，选择自然断点法将洪水风险等级划分为：高风险、较高风险、中风险、较低风险、低风险等5个风险等级；最后，基于历史洪灾，将AHP 法、熵权法与博弈论组合赋权法进行比较，验证所提出的方法对洪水风险管理的有效性，确定洪水风险区划，为洪水灾害管理提供合理建议，研究路线图见图2。

图2 研究路线Fig.2 Flow chart of the study

1.3 洪水风险评价指标体系

研究基于灾害风险理论，通过对致灾因子的风险性评估、孕灾环境稳定性的分析、承灾体易损性的评价来揭示区域的致灾机制［20］，并参考洪水风险的相关研究［6,7,21］，选取以下洪水风险评价指标：历史最大日降雨量（RF）、暴雨次数（RFT）、高程标准差（DEM）、归一化植被指数（NDVI）、水系距离（DR）、GDP 密度（GDP）、人口密度（POP），以下对指标内容、来源和处理方法进行说明。

1.3.1 致灾因子指标

（1）历史最大日降雨量（RF）：暴雨是引起武威洪水的主要原因，历史最大降雨则反映了洪水可能造成的最大损失。选择1961—2019 年中国地面降水日值0.5°×0.5°格点数据集，数据来自国家气象科学数据中心（http://data.cma.cn/），采用反距离权重插值法获得研究区域逐日降雨数据。

（2）暴雨次数（RFT）：暴雨发生越频繁的地区，未来发生洪水的可能性越大。根据武威0.5°×0.5°格点降雨数据，统计日降雨量30 mm以上的次数，采用Kriging插值法计算得到武威暴雨次数数据。

1.3.2 孕灾环境指标

（1）高程标准差（DEM）：高程标准差越大，表示格点附近的地形起伏越大，更易形成洪水。选择SRTMDEM 90M 分辨率原始高程数据，数据来自（https://www.gscloud.cn/search），通过GIS 邻域分析得到研究区高程标准差。

（2）归一化植被指数（NDVI）：植被直接影响产汇流过程，对洪水的形成时间和规模大小有着重要作用。数据来自中国科学院资源环境科学与数据中心（https://www.resdc.cn/）。

（3）水系距离（DR）：距离河流湖泊越近，越容易受到洪水侵袭。水系数据来自国家1：1000000标准矢量地图数据（https://www.webmap.cn/main.do?method=index），通过GIS 近邻分析得到区域内各点距水系距离。

1.3.3 承灾体指标 相同量级的洪水发生在不同的地区，所造成的损失是不同的，洪水具有社会属性，涉及到经济和人口要素。GDP 密度和人口密度数据均为1 km栅格数据，来自中国科学院资源环境科学与数据中心（https://www.resdc.cn/）。

确定评价指标体系后，对图层进行预处理，将各指标图层重采样为1 km分辨率，通过栅格计算器进行指标标准化，标准化方法见式（1）、（2），通过GIS 统计工具统计各评价指标熵值，进而计算熵权法指标权重。

1.4 熵权法

熵来源于热力学，用来描述分子运动的不可逆现象。在信息论中，熵反映了信息的无序化程度，可以用来度量信息量的大小，某项指标携带的信息越多，表示该项指标对决策的作用越大，此时熵值越小，即系统的无序度越大［22］。计算指标权重主要步骤如下：

（1）指标数据标准化：对于正向指标，也即越大越优型，按下式处理：

对于负向指标，即越小越优型指标，按下式处理：

式中：(aj)max为第j项评价指标的最大值；(aj)min为第j项评价指标的最小值；aij为第j项评价指标在第i个评价单元的指标值；rij为第j项评价指标在第i个评价单元标准化指标值。

（2）计算指标熵：

式中：当fij=0，fijlnfij=0，m为研究区的基本网格单元数；n为评价指标数量；Hj为指标熵。

（3）根据指标熵计算熵权，如下式：

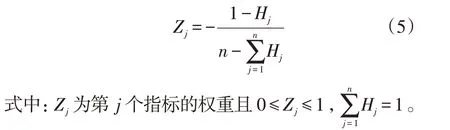
1.5 层次分析法（AHP）

层次分析法基本原理是：将评价系统的多种方案的各种要素分解成目标层、准则层、指标层，进行两两判断比较并计算出各要素的权重，根据综合权重按最大权重原则选出最优方案。层次分析法可操作性强，结构灵活，其基本步骤如下：

（1）构建研究系统的递阶层次：层次分析法首先要将所研究对象进行分层次化处理，一般可分为三层，即目标层、准则层、指标层。

（2）构造判断矩阵：对同一层次的不同要素进行两两判断，得到两两判断矩阵，为了对其重要性进行分级，通常采用1-9标度法。

（3）层次单排序：对本层次各要素重要性进行两两判断，从而计算出对上一层次的权重。

1.6 博弈论组合赋权

博弈论组合赋权广泛应用于自然灾害风险评价［23-24］，在博弈论中，假定各个方案都是理性决策的结果，其目的是寻求目标系统整体利益最优解。其最终结果不是由单一方决策者掌控的，而是由所有决策者共同实现的［24］。它可以归结为一个多主体的优化问题，其基本思想是在不同方法的权重之间寻找一致或妥协，即最终赋权结果与各个基本方法权重之间的偏差达到最小。

博弈论组合赋权的实质是不同赋权方法的结果进行综合，所以使用博弈论进行组合赋权结果前，要对2 种方法的赋权结果进行一致性检验。其中不同赋权方法的结果一致性程度可通过距离函数表示：

在通过一致性检验后，对2 种方法进行组合赋权，具体步骤如下：

（1）假设共采取L种方法对评价指标进行赋权，其中任一方法赋权结果的向量为ωk={ωk1,ωk2,…,ωkn} (k=1,2,…,L) ，则L个向量可任意线性组合为：

式中：ω为全部可能的组合权重向量；为单一方法赋权结果；βk为权重系数且规定βk＞0。

（2）为了求得最优的权重组合方法，就是使得博弈论组合赋权结果向量与各方法赋权结果向量离差最小，则最优权重系数依据下式求解：

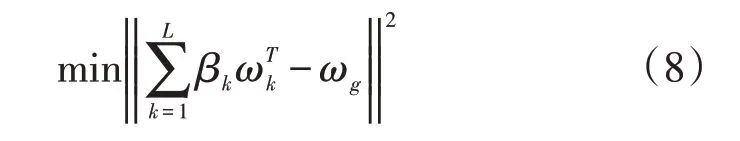
式中：ωg为博弈论组合赋权结果。

根据矩阵微分性质将式（8）展开可得以下线性方程，求解以下线性方程组便可得到最优权重系数：

（3）根据上列线性方程组求得最优权重系数后，对权重系数进行归一化处理，将归一化的最优权重系数带入式（7），得到博弈论组合赋权结果。

2 结果与分析

2.1 多方法对比分析

基于洪水风险灾害理论搭建评价指标体系，根据专家评价构建洪水风险评价指标判断矩阵，各层次指标权重均通过一致性判断。通过GIS分析工具计算洪水风险评价指标熵值，得到熵权法各评价指标权重。两者权重通过一致性检验，经博弈论组合赋权计算权重系数为：β1=0.525，β2=0.475。

根据表1，熵权法赋权结果显示对武威洪水风险影响较大的因子有人口密度、GDP密度及暴雨次数，忽视了高程标准差和水系距离等加剧洪水灾害危险性的环境因素；AHP法结果显示影响较大的因子有高程标准差、历史最大日降雨量和暴雨次数，缺少对人口密度和GDP 密度等洪水灾害易损性指标的考虑。

表1 洪水风险评价指标赋权结果Tab.1 Result of flood risk assessment index weighting

无论是基于数据的客观赋权方法，或是反映专家意见的主观赋权方法都未能综合考虑致灾因子危害性、孕灾环境稳定性和承灾体脆弱性三方面的要素，经过博弈论组合赋权，既能较好地反映专家的主观意愿，又能克服一些客观权重的不足。

由上述3种评价方法分别构建模糊综合评价模型，采用自然断点法对洪水风险进行分级，以验证组合赋权方法的有效性，生成洪水风险空间分布图（图3）。

图3 洪水风险图Fig.3 Flood risk map

熵权法得到的洪水风险图中，高风险和较高风险地区面积为3653 km2，占11.73%，较低风险和低风险地区面积为19252 km2，占61.80%；采用层次分析法的洪水风险图，高风险和较高风险地区面积为13800 km2，占44.30%，较低风险和低风险地区占38.10%；在组合赋权中，高风险地区和较高风险地区面积占34.81%，中风险地区占21.36%，较低风险和低风险地区面积为13656 km2，占43.84%。AHP法和熵权法所得到的洪水风险分区差异较大，说明采用不同赋权方法的洪水风险评价存在不确定性。

各赋权方法不仅在洪水风险面积上有较大差异，空间分布也存在不同。熵权法较组合赋权风险低估地区占56.34%，高估地区占2.88%，与组合赋权方法比较，评价一致地区占40.78%；AHP 法较组合赋权低估地区占8.24%，高估地区占37.86%，与组合赋权方法比较，评价一致地区占53.90%。AHP法与组合赋权法洪水风险分布一致性较高，而熵权法则较组合赋权法低估。

2.2 历史洪水验证

根据《中国气象灾害大典》《中国气象灾害年鉴》和相关文献［18］统计历史洪水，将历史洪水分别在熵权法、AHP法和博弈论组合赋权洪水风险图中进行叠置分析，可以得到该地区的洪水风险评价等级；根据相关研究［18］将历史洪水分为5 个等级，洪水次数＞13 为高风险，10 ＜洪水次数≤13 为较高风险，8 ≤洪水次数≤10 为中风险，5 ≤洪水次数＜8为较低风险，洪水次数＜5 为低风险。比较后的结果如表2。由于洪水风险评估主要关注中高风险地区，首先对中风险及以上洪水地区进行验证，AHP法在这些地区多为高估，与历史评价一致地区占26.31%；而熵权法有较大低估，特别未能识别出高风险地区，评价一致地区仅占21.05%；组合赋权方法结果最为准确，但在中风险地区有所高估，与历史一致地区占42.11%。针对较低和低风险地区，3种方法都存在一定高估，其中熵权法表现最好。因此博弈论组合赋权更能反映武威市洪水风险分布规律，既能准确识别洪水脆弱区，也不高估洪水风险，故下文仅对组合赋权洪水风险图进行分析。

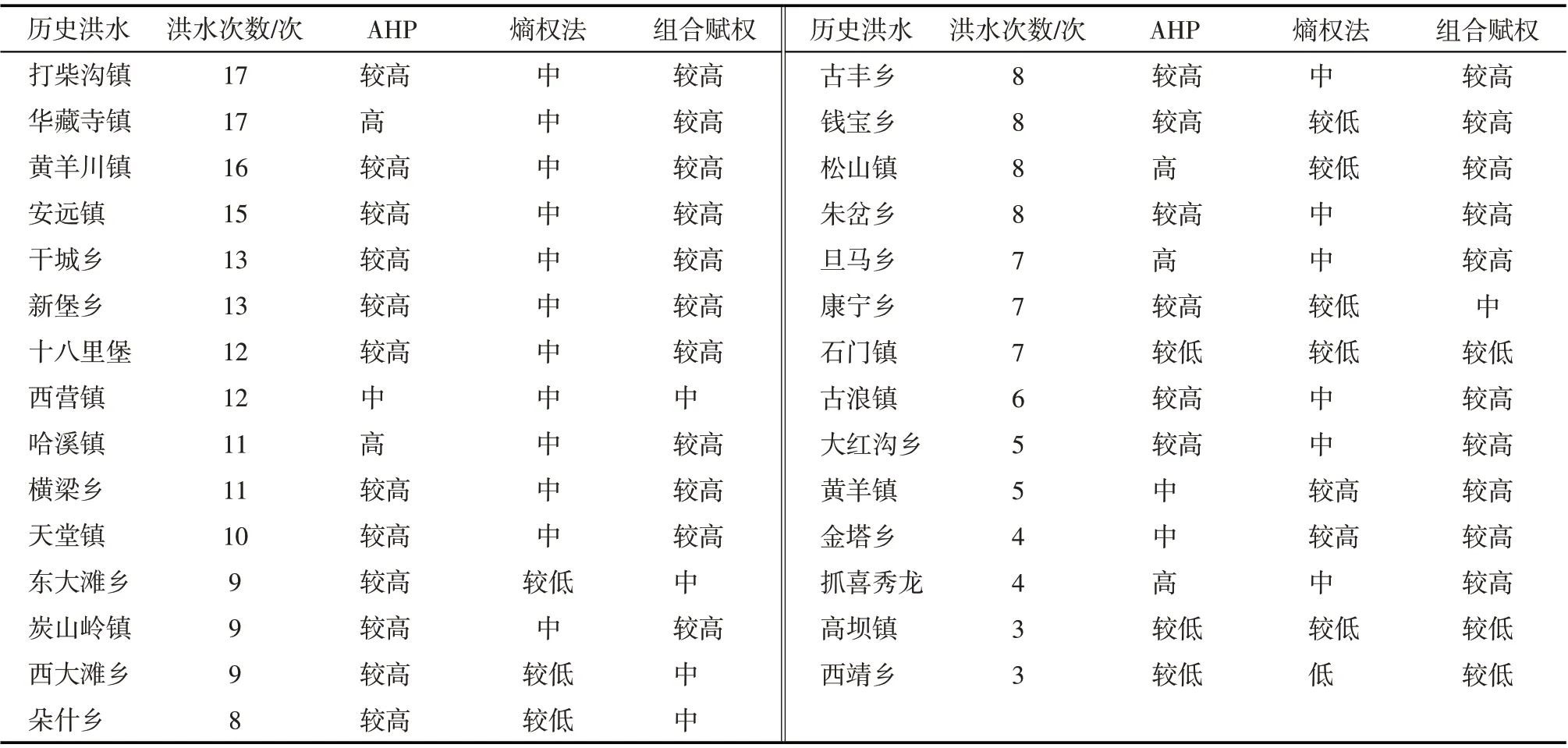
表2 历史洪水多发区洪水风险评价Tab.2 Flood risk assessment in areas prone to historical floods

2.3 洪水风险区划分析

通过研究区洪水风险区划分析，可以确定子区域洪水风险等级和风险来源，由图4 可以获得武威市整体及其行政区不同洪水风险等级占比和影响区域洪水风险的主要因素。武威市洪水风险由西南向东北递减，高风险地区集中在凉州区西南部的石羊河上游、西营河、五坝河、黄羊河和沙沟河和天祝藏族自治区西南部的干沙河、毛藏河。凉州区高风险区占总面积14.53%，导致地区洪水风险较高的主要原因是承灾体脆弱性较高，凉州区西南部地处祁连山脉北麓，河网密集，降雨集中，人口密度大，经济发达，发生洪水会造成严重损失。而天祝藏族自治县较高的洪水风险来源于致灾因子危险性，天祝藏族自治县西南部受到祁连山脉影响，降雨频繁，易产生较大暴雨。低风险地区主要集中在民勤县东部沙漠区，占总面积的56.28%，主要原因是民勤县位于腾格里和巴丹吉林两大沙漠相交处，造成该地独特的沙漠气候，历史降雨稀少，蒸发强烈，储水能力差，石羊河在此内流进入沙漠，整体河网稀疏，人口密度较小。

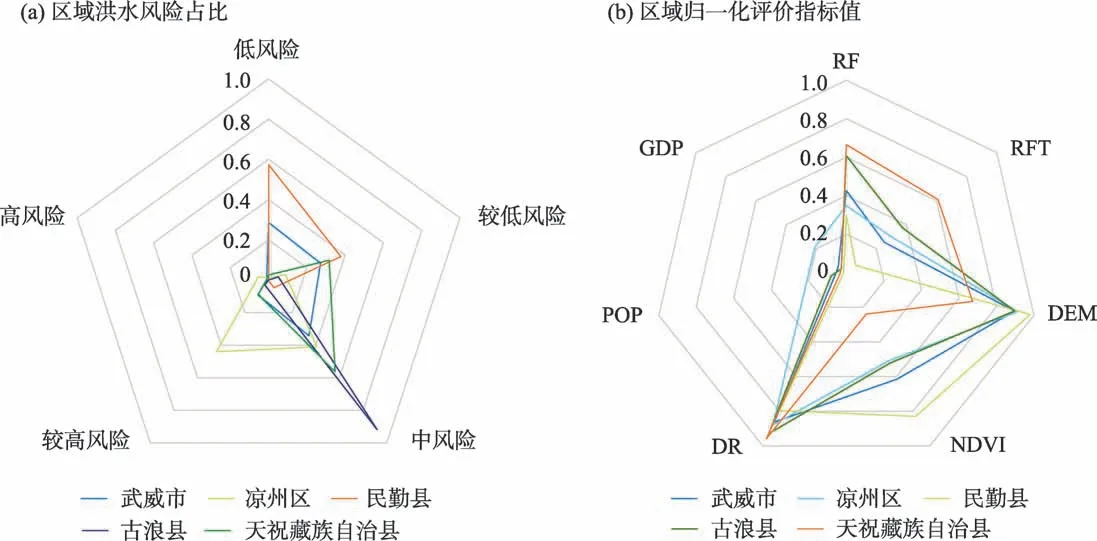
图4 洪水风险区划分析Fig.4 Flood risk zoning analysis

3 结论

对武威市洪水风险进行评估，根据研究获得的武威市洪水风险图与实测历史洪水资料，以及研究区洪水风险相关研究的洪水风险图进行比较，结果显示该研究对于武威市洪水风险区划判断比较准确。得到以下结论：

（1）采用主客观权重相结合的博弈论组合赋权方法，可以减少单一方面的局限性，提高洪水风险图的精度。

（2）武威市整体洪水风险等级为较低风险。洪水风险呈现由西南向东北递减的分布特征，高风险集中分布于凉州区与古浪县交界处以及天祝藏族自治区西南部，低风险地区主要分布在民勤县内的沙漠区。高风险地区只占4.94%，较低风险和低风险地区面积占43.84%。

（3）武威市各县区洪水风险的主要来源各不相同。致灾因子危险性呈现由西南向东北递减的带状分布特点，高危险区主要分布在天祝县祁连山脉地区，低危险区集中在东北部的石羊河下游。孕灾环境稳定性分布较为均匀，除祁连山区稳定性较高，中部河西平原区及东部沙漠区稳定性相近。承灾体脆弱性地区差异性明显，凉州区与古浪县交界处脆弱性远高于其他地区。