近60 a石羊河流域蒸发量变化及其原因分析
李小琴, 冉 宸, 张晓霞, 冉新民
(1.兰州资源环境职业技术大学,甘肃兰州 730050;2.浙江省水利河口研究院(浙江省海洋规划设计研究院),浙江杭州 310000;3.舟曲县城关九年制学校,甘肃舟曲 746300;4.兰州大学资源环境学院,甘肃兰州 730000)
蒸发是水循环的关键环节,也是流域或区域水量平衡的重要组成部分[1],尤其对于干旱区大型水体,如水库、湖泊等[2-3]。近年来,随着我国干旱区水资源供需矛盾进一步加剧,水面蒸发的计算越来越受到水文气象预报、防灾减灾、水资源评价、涉水工程规划等领域的关注[4]。因此,分析水面蒸发的时空变化特征及其影响因素具有十分重要的意义。
目前,水面蒸发观测最常用的方法是蒸发皿,该方法通常在水体之上或周边设立水文站,通过观测蒸发皿蒸发估算水面蒸发数值[5]。在实际应用中,受部分地区无观测资料或观测资料序列较短等限制,采用模型估算水面蒸发成为主要的选择[6-9]。由于蒸发皿侧壁引起的边际效应及蒸发皿本身与周围环境的异质性引起的绿洲效应,使得蒸发皿蒸发往往不同于水面蒸发[10]。因此,Rotstayn等[11]通过耦合影响蒸发的辐射组分[10]和空气动力学组分[12]拓展了精确模拟Class-A 型蒸发皿蒸发的物理模型,以下简称“PenPan 模型”。该模型被成功应用于美国[13]和澳大利亚[14-15]等Class-A 型和中国φ20 cm 型[16-17]蒸发皿蒸发模拟,但很少被应用于E-601型蒸发皿蒸发估算。Yu 等[18]将之应用于极端干旱区平原湖泊E-601 型蒸发皿蒸发模拟,通过对净辐射计算方法的改进,显著提高了该模型的模拟效果;孙继成等[19]在此基础上采用改进的模型有效地模拟了石羊河流域上游山区水库的水面蒸发,但该模型在整个流域内不同环境条件下的蒸发量估算鲜见报道。
石羊河流域位于我国西北地区中段,甘肃省河西走廊东部,是河西走廊第三大内陆河。自20世纪50 年代以来,随着气候变化及人类活动的影响,流域内水资源开发利用矛盾异常凸显,生态环境不断恶化[20-21],因此,石羊河流域水资源的高效利用成为流域管理长期关注的研究课题,而作为水资源消耗主要路径的蒸发估算成为基础性科学问题。本文以石羊河流域内的4 个气象站1958—2017 年蒸发皿蒸发为观测资料,结合其他气象要素和改进的PenPan模型模拟蒸发量变化,并分析引起蒸发量变化的原因,以拓展该模型在干旱区内陆河流域水面蒸发估算中的应用。
1 研究区概况
石羊河流域位于甘肃省河西走廊东部(图1),乌鞘岭以西,祁连山北麓,地理位置为101°41′~104°16′E,36°29′~39°27′N 之间。地势从西南向东北倾斜,海拔1182~5214 m。流域总面积4.16×104km2,包括8条支流,从东到西依次为:大靖河、古浪河、黄羊河、杂木河、金塔河、西营河、东大河和西大河。石羊河流域从南到北涵盖了3 个气候区,南部祁连山区为高寒半干旱半湿润区,海拔2000~5000 m,年平均气温2~6 ℃,年降水量为300~600 mm,年蒸发量为700~1200 mm,干旱指数(降水/蒸发)为0.25~1;中部走廊平原为干旱区,海拔1500~2000 m,年平均气温6~8 ℃,年降水量为150~300 mm,年蒸发量为1300~2000 mm,干旱指数为0.07~0.25;北部为极端干旱区,海拔1200~1500 m,年平均气温大于8 ℃,年降水量低于150 mm,年蒸发量为2000~2600 mm,干旱指数为0.04~0.07。其中,最北部的民勤绿洲年降水量不足50 mm,年降水季节分配不均,90%的降水集中在5—10月[20-21,26]。

图1 研究区位置及气象站点分布Fig.1 Location of study area and meteorological stations
2 数据来源与方法
2.1 气象数据
石羊河流域内共有4 个国家气象站,自南向北沿海拔梯度递减为:乌鞘岭站、永昌站、武威站和民勤站(表1)。另外,由于流域内水文站的时间序列相对较短,很难分析长时间序列的变化趋势。考虑到数据序列的完整性和一致性,选择1958—2017年连续60 a的气象资料作为分析数据,数据来源于国家气象科学数据中心:http://data.cma.cn。

表1 石羊河流域主要气象站点信息Tab.1 Information of major meteorological stations in the Shiyang River Basin
2.2 水面蒸发观测
水面蒸发观测依据《水面蒸发观测规范》(SL 630—2013):非冰期(4—9 月)采用E-601 型蒸发皿观测,冰期(10月—次年4月)采用φ20 cm型蒸发皿观测,1998—2001 年结冰前(9 月)、融冰后(5 月)采用2 种仪器同时观测,据此计算φ20 cm 型蒸发皿与E-601 型蒸发皿之间的折算系数。在资料整编时,将1—4 月的小型蒸发资料按5 月的实测折算系数换算为E-601型蒸发皿的观测资料;10—12月资料用9月实测折算系数换算[19]。
2.3 PenPan模型及参数化
Rotstayn 等[11]提出的Class-A 型蒸发皿蒸发量(EPenPan,mm·d-1)计算公式为:

式中:Δ为气温Ta的水汽压曲线斜率,kPa·℃-1;γ为干湿表常数,kPa·℃-1;ap为表征蒸发皿侧壁的额外热量交换常数,通常取2.4;Rn,Pan为蒸发皿上的净辐射,MJ·m-2·d-1;λ为水的汽化潜热,MJ·kg-1;es-ea为水汽压差,kPa;f(u)为2 m高度处风速(u2)的函数[20],m·s-1。f(u)可表示为:

由式(1)可见,PenPan模型将蒸发分为两部分,前面部分为辐射项,主要受净辐射影响;后面部分为空气动力学项,主要受到风速和水气压差影响。
该模型中,Rn,Pan的计算是最关键的,其表达式为:


式中:αA为Class-A 型蒸发皿水体反照率,取常数0.14;Rs,Pan为蒸发皿接收的总短波辐射,MJ·m-2·d-1;αss为蒸发皿周围地面的反照率;Rs和Rnl分别为总辐射和净长波辐射,MJ·m-2·d-1;fdir为直接辐射Rs的占比。fdir可表示为:
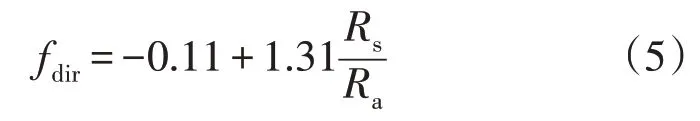
式中:Ra为地外辐射,MJ·m-2·d-1。
Prad为蒸发皿辐射因子,表示为:

式中:lat为纬度绝对值,(°)。
以上公式中Δ、γ、λ、es-ea、Rs、Ra、Rnl计算参见文献[22]。
Yu等[18]提出在模拟E-601型蒸发皿蒸发时,直接采用Rn代替Rn,Pan(以下简称“改进的PenPan 模型”)使得模型更简单,应用更方便,精度更高。其中:Rn计算需要站点的经纬度、海拔和日照时数,详细计算方法参见文献[23]。
2.4 模型评价
本文选择验证水文模型模拟效果优劣常用的决定系数(R2)、均方根误差(RMSE)和纳什效率系数(NSE)进行模型评价,其表达式分别为:
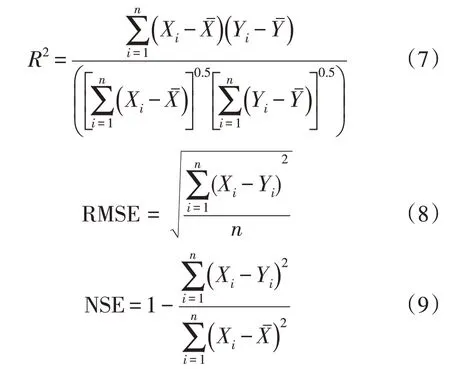
式中:Xi为蒸发量的观测值;Yi为蒸发量的模拟值;和分别为蒸发量观测值和模拟值的平均值。NSE越接近于1,表示模拟效果好,模型可信度高。
以上所有统计分析、参数计算采用SPSS 19.0(IBM SPSS Statistics, Inc, USA)完成,制图采用SigmaPlot 14.0(Systat Software,Inc,USA)完成。
3 结果与分析
3.1 蒸发量变化
由图2可见,随着海拔升高,年蒸发量呈递减趋势,下游平原的民勤站年蒸发量最大,为1530.7 mm,上游山区的乌鞘岭站年蒸发量最小,为892.7 mm,中部的永昌站和武威站年蒸发量适中,约为1174.5 mm。需要说明的是,中部的武威站和永昌站蒸发量相差不大,但武威站的海拔要低于永昌站,约500 m;武威站蒸发量低可能与该气象站位于城市内部,风速较低,空气动力组分不足有关。若不考虑武威站,其他3 个站点的年蒸发量与海拔变化呈显著的负线性关系(R2=0.96,P<0.001),递减率为38 mm·(100m)-1,即海拔每升高100 m,蒸发量降低38 mm。就蒸发的海拔效应而言,王金叶等[24]研究表明:祁连山林区(φ20 cm 蒸发皿)蒸发量随海拔(1680~3800 m)每升高100 m 递减48. 41 mm,选取张掖站2 种蒸发皿折算系数为0.6118[25],则递减率为29.6 mm·(100m)-1,低于本研究结果,原因是本研究区的海拔梯度大于山区。海拔通过影响温湿度间接地影响着蒸发的时空变化,另外,包括气象站点所在位置、人类活动等(如武威站蒸发量略低)。
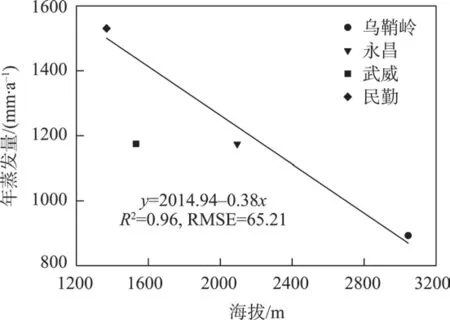
图2 石羊河流域年蒸发量随海拔的变化Fig.2 Changes of yearly evaporation along with altitudinal gradients for the Shiyang River Basin
石羊河流域沿海拔梯度递减的4个气象站日平均蒸发量分别为2.44±0.16 mm·d-1、3.20±0.16 mm·d-1、3.21±0.14 mm·d-1和4.19±0.19 mm·d-1,蒸发量自南向北逐渐增大。各气象站蒸发量年内变化趋势一致,大致从3 月开始增大,在5—7 月达到最大值,8月后开始减小,直至冬季(图3a);就累积年变化而言,3月之前各气象站蒸发量基本一致,之后差距逐渐增加,10 月之后增速变缓。同样地,各气象站月平均蒸发量亦呈自南向北递增趋势,月蒸发量以6月或7 月最高,12 月或1 月最低,不同季节表现为:冬季低、夏季高、春秋季居中的特点(表2)。

表2 石羊河流域1958—2017年蒸发量月变化Tab.2 Monthly variation of evaporation in 1958-2017 for the Shiyang River Basin/mm
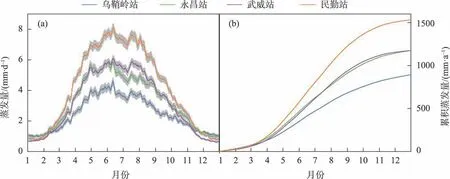
图3 石羊河流域年内日蒸发量(a)和累积蒸发量(b)变化Fig.3 Changes of daily evaporation within the year(a)and accumulated in one year(b)for the Shiyang River Basin
石羊河流域蒸发量年际变化如图4所示。长期来看,近60 a蒸发量变化趋势存在明显空间差异,上游山区的乌鞘岭站和下游的民勤站呈减少趋势,递减率分别为4.67 mm·(10a)-1和0.58 mm·(10a)-1,而中部的永昌站和武威站呈显著的增加趋势,增长率分别为17.86 mm·(10a)-1和13.95 mm·(10a)-1(图4a)。但是,从累积距平(平均值-当年值)曲线来看,年蒸发量存在明显的突变点。永昌、武威和民勤的蒸发量变化大致分为2 个阶段,1958—1969 年累积距平为负,即蒸发量逐年下降,1970—2017 年累积距平为正,即蒸发量逐年增加;而乌鞘岭在1958—1990 年累积距平为负,呈下降趋势,1990 年之后累积距平为正,蒸发量有所增加。这一结果与刘蕊蕊等[26]的研究结论是不一致的,本研究中石羊河流域20 世纪70 年代以前蒸发量显著下降,但之后是显著增加的,尤其是中下游地区。

图4 石羊河流域年蒸发量(a)和(b)累积距平变化Fig.4 Changes of yearly evaporation(a)and accumulative anomaly(b)for the Shiyang River Basin
3.2 模型模拟与验证
已有研究表明:改进的PenPan模型可以较好的模拟我国常用的E601型蒸发皿蒸发[18-19],本文的结果也证实了这一结论(图5和图6)。在日尺度上,改进的PenPan 模型估算的蒸发量与观测值均呈显著的线性关系,模型的R2>0.85,而RMSE≤1,NSE>0.3,但模型整体高估了蒸发量约10%~20%,尤其是在蒸发量较大时;另外,模型在平原区的模拟效果要优于山区,随着海拔增加,模型模拟值则高于观测值,如海拔最高的乌鞘岭站模拟值较观测值偏高20%(图5a)。模型效果优于孙继成等[19]对石羊河流域上游水库蒸发量的模拟。在月尺度上,模型的模拟效果要比日尺度上更优,模型的R2>0.94;但是,模型模拟值更加高于实际观测值,尤其是对高海拔区的乌鞘岭站模型高估了37%,NSE 甚至小于0(图6),这可能主要受风速影响,因风速是随着海拔升高而增加的。综上所述,改进的PenPan模型能够较好的模拟石羊河流域不同海拔站点的蒸发量,但模型还有待进一步修正,尤其是对风速函数f(u),在不同地区应用存在不同的表达形式[11-12,21]。

图5 石羊河流域日蒸发量模拟值与观测值关系Fig.5 Relationship between the simulated and observed daily evaporation for the Shiyang River Basin

图6 石羊河流域月蒸发量模拟值与观测值关系Fig.6 Relationship between the simulated and observed monthly evaporation for the Shiyang River Basin
3.3 蒸发变化的成因分析
影响水面蒸发的因素是多方面的[13,16,26],但总体上可分为两大类,即辐射因子和空气动力学因子[11]。基于改进的PenPan 模型计算的石羊河流域蒸发量的辐射组分和空气动力学组分变化具有各异的特征,受净辐射控制的辐射组分变化相对稳定,但受饱和水气压差和风速控制的空气动力学组分波动较大(图7)。高海拔区的乌鞘岭站和永昌站辐射组分相对较低,且与空气动力学组分大小相当;低海拔区的武威站和民勤站的辐射组分大致相当,但武威站的辐射组分明显高于空气动力学组分,民勤站则相反。对比图4 与图7 可见,引起蒸发量年际差异的主要原因是空气动力学组分的变化。根据PenPan模型可知,影响空气动力学组分变化的主要因素是水气压差和风速。由图8 可见,近60 a 水气压差变化也存在明显的2个阶段,20世纪70年代之前呈下降趋势,之后缓慢变化,90 年代初开始迅速增加,风速变化与之相反。这与Mann-Kendall 检验结果基本一致[26]。温度与饱和水气压差变化趋势基本一致,净辐射除乌鞘岭站外基本无变化。由此可见,引起石羊河流域平原区蒸发量变化的主要原因还是温度,即随着全球变暖,温度升高,水气压差增加,蒸发量增加,温度与蒸发量变化是一个正反馈过程。

图7 石羊河流域蒸发量辐射和空气动力学组分年际变化Fig.7 Yearly change of radiative and aerodynamic components of evaporation for the Shiyang River Basin

图8 石羊河流域气象因子距平年际变化Fig.8 Yearly change of anomalies of meteorological factors for the Shiyang River Basin
也有研究表明,20世纪70年代以来蒸发量是减少的。例如,Yang 等[16]对全国54 个站点1961—2001年蒸发量变化的分析表明,全国范围内蒸发量总体呈下降趋势,递减率为3.1 mm·a-1,辐射和风速减弱是造成蒸发量下降的主要因素,但区域之间存在差异,尤其是在石羊河流域的4 个气象站存在各异的结果:显著增加、显著减少和无显著变化共存。Xie 等[17]研究表明:青藏高原1970—2012 年蒸发量呈递减趋势,递减率为11.8 mm·a-1,风速下降和辐射减弱是引起蒸发量下降的主要原因。本研究中,只有高海拔区的乌鞘岭站蒸发量在1970年后呈下降趋势,风速亦然,但温度增加。由此可见,蒸发量的变化及其原因存在明显的区域差异,就石羊河流域而言,由于该区地处黄土高原、青藏高原和内蒙古高原的交汇过渡带,气候系统复杂,造成不同海拔区蒸发量年际变化各异的原因还有待进一步研究。
Yu等[8]对全国不同气候带178个气象站蒸发量模拟研究表明,温度驱动的模型在温带大陆性气候区具有最优的表现,温度是影响蒸发量变化最主要的因子。Celestin 等[9]对河西走廊蒸发量采用32 个简单模型模拟效果的评价表明,仅考虑风速和饱和水气压差的空气动力学模型表现最优。刘蕊蕊等[26]采用灰色关联度分析的结果表明,影响石羊河流域蒸发的主要因子是温度和风速。已有研究表明,未来石羊河流域气温仍将呈上升趋势,这与全球尤其是北半球气候变暖存在着某种程度的一致性[27]。温度的上升必将引起流域蒸发量的增加,给未来水资源的可持续利用和管理带来极大地不确定性。
4 结论
水面蒸发的准确量化对于水资源合理调度、水资源精细化管理等具有重要的实践意义。本文以石羊河流域为例,采用改进的PenPan模型分析了流域蒸发量的时空变化及其原因,得出以下结论:
(1)石羊河流域蒸发量的空间变化存在海拔效应,即随着海拔的增加蒸发量显著减少,递减率约为38 mm·(100m)-1;时间变化存在明显的分段特征,1958—1970年是减少的,但20世纪70年代以后是增加的。
(2)改进的PenPan 模型能较好地模拟不同站点日尺度和月尺度的变化,但模型还有待进一步修正,尤其是对于风速函数。
(3)基于改进的PenPan 模型的组分分析表明,引起20世纪70年代以后蒸发量增加的主要原因是空气动力学组分的增加。其中,中下游地区的温度与蒸发量变化是正反馈过程,而上游高山区与之相反。未来,石羊河流域气温可能将持续升高,进而引起蒸发量的增加。因此,建议在流域农业灌溉、重大涉水工程(尤其是水库)规划、气候变化应对政策制定等应用中全面综合考虑蒸发的影响。

