基于滑模控制的接触网/受电弓系统抗振动分析

王明雨

（南昌铁路勘测设计院有限责任公司，江西 南昌 330000）

1 接触网/受电弓系统的研究

接触网和受电弓作为铁路中的重要设备，一直受到众多学者和从业人员的关注。自20 世纪90 年代起，众多学者针对接触网/受电弓组成的耦合系统进行了大量的研究。文献[6]结合CH160-0 模型，建立了接触网有限元模型和受电弓运动微分方程，最后推导出弓/网系统的耦合动力学模型。文献[7]设计一种可实时进行模糊运算、推理的模糊控制器，实现了弓/网混合模拟系统中液压伺服系统的模糊控制。文献[8]采用负驰度的方法对接触网进行重构，进一步优化了弓/网系统的动力学计算。

2 接触网/受电弓系统的2个重要指标

在弓/网系统中，受电弓直接和接触线相接触从而获取电流，因此受流质量直接影响了铁路安全运行。文献针对单弓和双弓作用下接触网的稳定性进行对比，最后得出了双弓间距对机车受流质量的影响，对机车双弓间距提出了具体的要求。受电弓的抬升力对接触悬挂产生机械作用，使接触线升高。升高过低，压力值偏小，受流时容易出现离线并产生电弧，从而损坏接触线和弓头，影响正常的受流。升高过高，压力值偏大，受电弓和接触线的机械磨耗也越大，影响设备的使用寿命，也会使接触线过分升高，影响绝缘，甚至出现刮弓事故。同时，受电弓沿着接触线高速滑动会产生振动，振动会导致接触线抬升、弓/网之间的动态接触压力发生变化等问题，在振动超过一定范围后，弓/网系统会产生离线等现象，也严重威胁着列车的安全运行。因此接触线的动态抬升位移和弓/网之间的动态接触压力是衡量铁路安全运行的2 个重要指标。

3 如何抑制接触网/受电弓系统的振动

为了抑制振动，可以从受电弓和接触网等多个方面进行研究。在受电弓方面，选择归算质量更小、具有阻尼和缓冲装置的受电弓可以减少因为受电弓而产生的振动问题。在接触网方面，作为设计人员，一般会降低接触线的坡度、采用弹性链型悬挂和使用弹性较高的线索等方式降低接触线的振动。但是在列车高速运行弓/网系统剧烈摩擦的情况下，振动现象是不可避免的，因此在设计中，会允许弓/网之间的动态接触压力和动态抬升位移在一定范围内波动，一般接触压力在50N～200N，抬升位移限制在100mm～200mm,从而保证列车的正常受流。值得关注的是，在仿真实验中，经常会遇到弓/网之间动态接触压力为0的情况，该情况说明弓/网之间存在离线等问题，须避免。

4 滑模控制抑制振动的原理

在列车运行中，接触线的动态抬升位移与弓/网之间的动态接触压力是随着时间、跨距等因素变化的，在一个跨距内不同位置会出现不同的振动大小，因此分析弓/网之间的动态变化对抑制振动具有非常重要的意义。滑模控制理论具有快速响应、对外界扰动变化不灵敏的特点，大量应用在机械、航天、交通等领域。通过理想值与实际值的误差作为滑模面函数是常用的滑模控制方法，该文将滑模控制应用到受电弓伺服控制系统中，将弓/网系统的理想动态位移与实际动态位移之差作为滑模控制函数，从而控制受电弓的升降，减少接触线的动态抬升位移，最终实现抗振动的效果。

5 预备知识

5.1 接触网/受电弓模型

受电弓是一个复杂的机械机构，它包括弓头、上框架、推杆、平衡杆等构件，各个构件之间通过铰链座铰接，各铰接处还装有滚动轴承等以此控制受电弓的上升与下降。在通常的研究中，学者们会把受电弓分为3 个部分：弓头、上框架、下框架。弓头是机车和接触网接触获取电流的装置，弓头会随着接触线的升高或降低运动，实现弓/网之间接触压力的动态变化，因此弓头的质量好坏对机车能否正常、安全受流至关重要。上框架、下框架实现了受电弓的机械运动，它们与弓头之间相互绝缘，通过传动机构、伺服电机等实现对弓头位置的控制。

相对弓/网之间的动态接触压力，静态接触压力对弓/网系统的稳定性也至关重要。静态接触压力是指机车未运动之前，受电弓上升与接触线相接触，这时，受电弓对接触线会存在一个接触压力，该压力即为静态接触压力。静态接触压力偏大，弓/网之间接触磨损就越大，器械的使用寿命就会变短；压力偏小，受电弓无法和接触网实现有效的接触，从而影响机车的安全运行，因此讨论弓/网之间的接触压力对抑制振动具有重要意义。

在研究接触网/受电弓时，首先需要把相关设备模型化，便于研究。该文以DSA250 型受电弓为研究对象，将DSA250型受电弓简化为三质量模型，如图1 所示。

图1 受电弓物理模型

受电弓的阻尼可以维持弓/网之间的稳定性，确保受电弓处于相对平稳的状态，从而保证机车的受流质量。

5.2 弓/网系统动力学平衡模型

弓/网系统是由接触网和受电弓组成，需要对接触网和受电弓进行建模，统一到同一个数学模型中，以此来描述弓/网系统的运动状态。采用文献[9]中给出的弓/网系统的动力学平衡方程组：

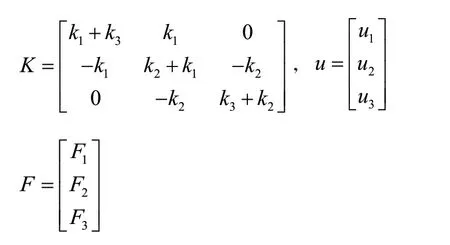
6 滑模控制协议设计

滑模控制方法对外界干扰不灵敏，可以降低外界因素对系统的影响。一般情况下需要先设计滑模误差函数，然后以误差函数为基础设计滑模面函数，最后设计滑模控制协议使系统运动到滑模面上，然后保持在滑模面附近运动。

在设计滑模控制协议之前，首先设计滑模误差函数。以弓/网系统弓头、上框架、下框架的实际动态位移和设计的理想动态位移之差作为误差函数。该误差函数如公式（2）所示。

式 中：（t）=[（t）（t）（t）]，（t），（t），（t）分别表示弓头、上框架、下框架在t时刻的误差函数。（t）=[（t）（t）（t）]，（t），（t），（t）分别表示弓头、上框架、下框架在t时刻的实际动态抬升位移，（t）=[（t）（t）（t）]，（t），（t），（t）分别表示弓头、上框架、下框架在t时刻的理想动态抬升位移。

以式（2）中的误差函数设计滑模面函数，如公式（3）所示。

式中：（t）是设计弓/网系统的滑模面函数，为增益函数。

接下来以滑模面函数式（3）为基础设计滑模控制函数，该控制函数将会“驱使”弓/网系统的动力学方程组式（1）沿着式（3）中设计的滑模面函数运动，最终收敛到滑模面函数（t）=0 附近，之后维持在滑模面函数（t）=0 附近运动，从而实现弓/网系统的抗振动。设计滑模控制函数如公式（4）所示。

式中：（t）为设计的滑模控制函数，h 为采样周期，、以及为增益函数，sgn 为符号函数，[-sgn（（t））-δ（t）]项为切换函数。

从滑模控制函数式（4）中可以看出，滑模控制函数以弓/网系统弓头、上框架、下框架的实际动态抬升位移与理想动态抬升位移之差为基础，采用符号函数sgn 控制弓/网系统的运动状态，“驱使”系统沿着设计的滑模面函数式（3）做上下切换运动，从而维持系统的运动状态，实现接触网的实际动态抬升位移向着理想的抬升位移运动，最终达到抗振动的效果。

7 仿真分析

该文在MATLAB/Simulink 平台中对所提算法进行验证。仿真中接触网的跨距为3 跨，接触网总长180m，导高1.4m，单跨吊弦数目为7，采用已知数据的接触线和承力索组合，仿真列车时速为160km/h。选用DSA250 型受电弓参数为=7.51kg，=5.855kg，=4.645kg，==0，=70（N·s·m），=8380（N·m），=6200（N·m），=80（N·m），=70N。

选用承力索、受电弓为THJ95+CTHA120 组合模型，接触网基本参数见表1。控制增益函数=1.5，采样周期=0.1s，=2，=5，=1，弓网系统节点在时刻的理想位移量[60 0 0]，单位是mm。在仿真中，仿真处未采用滑模控制方法情况下常规接触网和采用滑模控制函数式（4）两种情况下的动态抬升位移，通过两种情况下的接触网动态抬升位移做对比，从而体现出滑模控制函数式（4）的抗振动特性。

表1 仿真接触网系统参数

接触线的动态抬升位移和弓/网之间的动态接触压力仿真如图2 所示。

图2 常规接触网动态抬升位移与采用滑模控制接触网动态抬升位移对比

根据图2 可知，相较于常规的接触网动态抬升位移，采用滑模控制方法的接触网动态抬升位移较小一些，这说明滑模控制方法对弓/网系统的振动实现了抑制效果。接触线的动态抬升位移是以跨距为单位呈一定周期性变化，在支柱定位点附近动态抬升位移较小，在跨中附近动态抬升位移较大。同时也可以看出在第2、3 个跨距中，动态抬升位移相较于第1 个跨距较大，这是因为在第1 个跨距内产生的振动沿着接触线传播对第2、3 个跨距产生影响。从图3 中可知，弓/网系统的动态接触压力在40N～150N 变化，并且在仿真中没有出现动态接触压力为0 的情况，这说明弓/网之间没有产生离线现象，接触状态良好。

图3 弓/网系统动态接触压力

8 结论

针对弓/网系统产生的振动问题，该文采用抗外界扰动较强的滑模控制方法。首先，采用接触网的理想抬升位移和实际抬升位移之差作为滑模面的误差函数，随后根据切换协议设计了滑模控制函数。其次，通过MATLAB/Simulink 平台对所提出算法的有效性进行了验证，结果表明接触线的动态抬升位移有所下降，该控制协议对弓/网系统的抗振动起到了一定的效果。